Lựa chọn tối ưu hàm trọng số của bộ điều khiển H cho hệ thống ổn định ngang chủ động trên ô tô tải

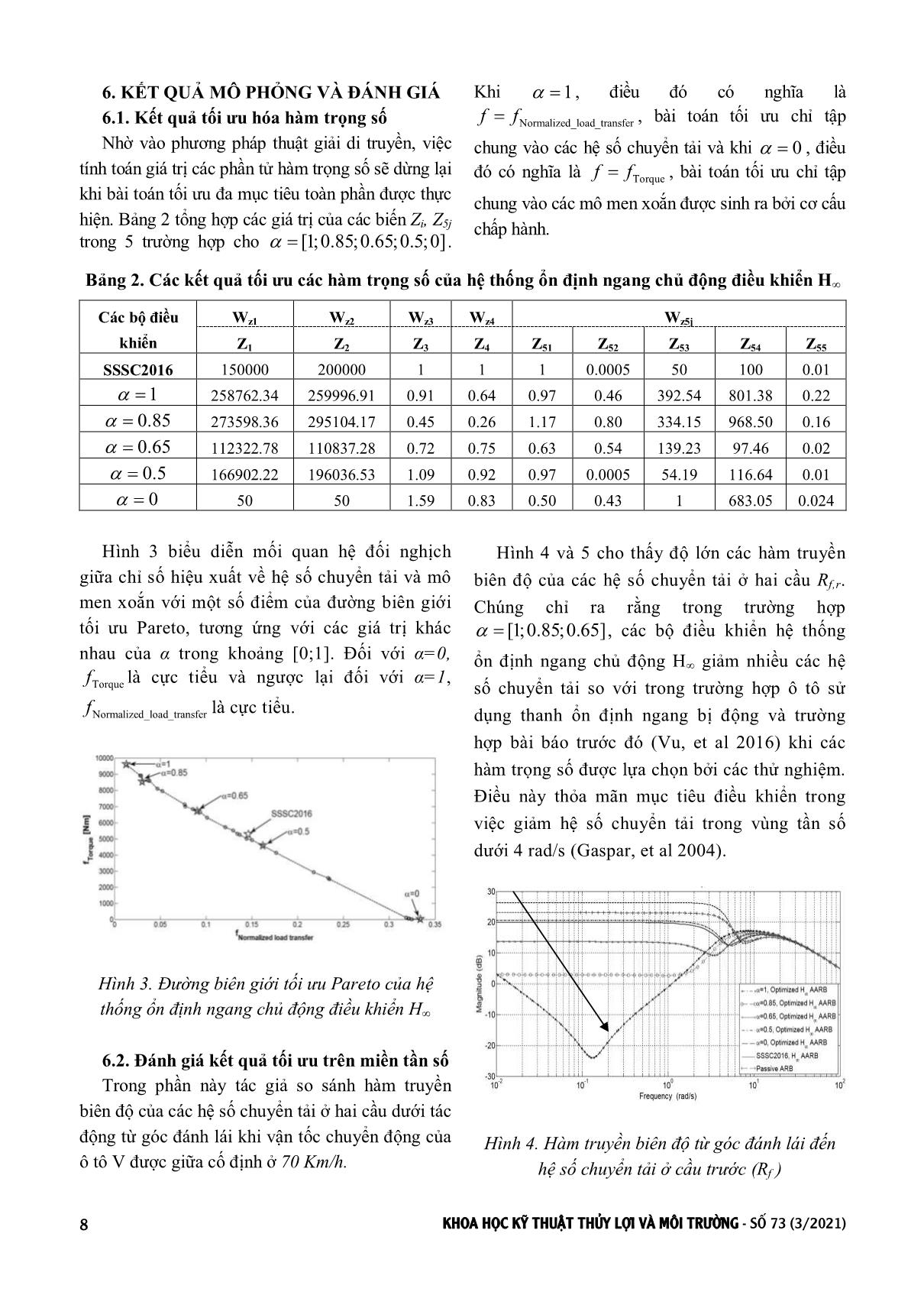
ác hàm đa mục tiêu véc tơ F 
được thay thế bằng tổ hợp lồi của các mục tiêu: 
1 1
min ( ), . , 1
obj objn n
i i i
i i
J f x s t x C 
   (2) 
Véc tơ 1 2( , ,..., )objn đại diện cho độ 
dốc của hàm J. Bằng cách sử dụng các bộ α khác 
nhau, người ta có thể tạo ra một số điểm trong tập 
Pareto, tức là hình thành đường cong ranh giới 
Pareto (Do, et al 2010). 
3. XÂY DỰNG MÔ HÌNH Ô TÔ TẢI HAI CẦU 
Hình 1 minh họa mô hình động lực học kết hợp 
theo phương lắc ngang và quay vòng của ô tô tải 
hai cầu bao gồm ba phần khối lượng chính: ms là 
khối lượng được treo, muf là khối lượng không 
được treo cầu trước bao gồm cụm cầu và bánh xe 
và mur là khối lượng không được treo cầu sau bao 
gồm cụm cầu và bánh xe. Các biến thông số mô 
hình và các giá trị được thể hiện trong (Gaspar, et 
al 2004), (Gaspar, et al 2005), (Vu, et al 2016). 
Các phương trình vi phân thể hiện mô hình ô tô 
như công thức (3), bao gồm: cân bằng lực bên 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 73 (3/2021) 5 
trong công thức (a); cân bằng mô men xoắn quanh 
trục OZ trong công thức (b); cân bằng mô men lật 
ngang của khối lượng được treo quanh trục OX 
trong công thức (c); cân bằng mô men lật ngang 
của khối lượng không được treo quanh trọng tâm 
cầu trước là (d) và cầu sau là (e). 
Hình 1. Mô hình động lực học của ô tô tải hai cầu (Gaspar, et al 2004) 
(3) 
Trong đó Uf, Ur là các mô men xoắn tại hai cầu 
được tạo ra bởi hệ thống ổn định ngang chủ động; 
Fyf , Fyr là hai lực bên của lốp; MARf , MARr là các 
mô men của thanh ổn định ngang bị động tác động 
đến khối lượng được treo và khối lượng không 
được treo cầu trước và cầu sau (Vu, et al 2016). 
Phương trình (3) có thể được viết dưới dạng 
không gian trạng thái như sau: 
 (4) 
Với véc tơ trạng thái: , 
véc tơ kích thích từ bên ngoài: fw  , véc tơ 
điều khiển đầu vào: f ru U U và véc tơ đầu 
ra: . 
4. TỔNG HỢP ĐIỀU KHIỂN H∞ CHO HỆ 
THỐNG ỔN ĐỊNH NGANG CHỦ ĐỘNG 
4.1. Mục tiêu điều khiển 
Mục tiêu của hệ thống ổn định ngang chủ động 
là để tối đa hóa độ ổn định ngang của ô tô. Thông 
thường, hiện tượng lật ngang xảy ra khi hệ số 
chuyển tải được tính toán (R) đạt đến ngưỡng 1 
(hoặc -1) (Gaspar, et al 2004). Hệ số chuyển tải 
 KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 73 (3/2021) 6 
R=±1 tương ứng với hệ số chuyển tải lớn nhất có 
thể của ô tô. Trong trường hợp vượt qua giá trị 
này thì một bánh xe của cầu xe sẽ nhấc lên khỏi 
mặt đường và hiện tượng lật ngang được xem xét. 
Để ô tô chuyển động ổn định thì giá trị hệ số 
chuyển tải phải đảm bảo không vượt quá ngưỡng 
giới hạn -1<R<1. 
Đặc tính hiệu xuất được quan tâm nhất khi thiết 
kế điều khiển cho hệ thống ổn định ngang chủ 
động là hệ số chuyển tải. Mục tiêu điều khiển 
được chọn là để giảm thiểu ảnh hưởng của góc 
đánh lái lên hệ số chuyển tải R, trong khuôn khổ 
của điều khiển bền vững H∞. Như đã giải thích ở 
phần trước, giới hạn của mô men xoắn Uf;r được 
tạo ra bởi bộ cơ cấu chấp hành cũng là rất quan 
trọng đối với việc triển khai lựa chọn lắm đặt hệ 
thống trong thực tế. 
Hình 2. Sơ đồ cấu trúc điều khiển G-K của 
bộ điều khiển H∞ cho hệ thống ổn định ngang 
chủ động 
4.2. Tổng hợp điều khiển H∞ cho hệ thống 
ổn định ngang chủ động 
Hệ thống vòng kín được trình bày trong Hình 
2, bao gồm mô hình danh nghĩa G, bộ điều khiển 
K và các hàm trọng số Wij. Trong sơ đồ này, Uf và 
Ur là đầu vào điều khiển, y1 và y2 là các tín hiệu 
đo được, n1 và n2 là các nhiễu đặc trưng của cảm 
biến. δf là góc đánh lái được coi là tín hiệu kích 
thích bởi người lái xe. Các biến z1, z2, z3, z4 và z5 
tượng trưng cho hiệu suất đầu ra. 
Theo Hình 2, việc ghép mô hình tuyến tính (4) 
với các hàm trọng số dẫn đến biểu diễn không 
gian trạng thái của P(s) như sau: 
(5)
Với đầu vào nhiễu bao gồm: 1 2[ ]W d n n , 
đầu vào điều khiển: [ ]Tf rU U U , đầu ra hiệu 
suất: 1 2 3 4 5[ ]
TZ z z z z z , đầu ra đo được: 
. 
5. LỰA CHỌN TỐI ƯU HÀM TRỌNG SỐ 
CỦA BỘ ĐIỀU KHIỂN BỀN VỮNG H∞ 
5.1. Mục tiêu tối ưu 
Mục tiêu của hệ thống điều khiển ổn định 
ngang chủ động là tối ưu hóa ổn định ngang của ô 
tô để ngăn ngừa hiện tượng lật ngang trong các 
trường hợp nguy hiểm. Tuy nhiên, mục tiêu hiệu 
suất như vậy phải được cân bằng với năng lượng 
tiêu thụ của hệ thống được đặc trưng bởi mô men 
xoắn tạo ra bởi cơ cấu chấp hành. Do đó, hàm 
mục tiêu được chọn như sau: 
Normalized_load_transfer Torque(1 )f f f (6) 
Trong đó Normalized_load_transferf và Torquef là các 
chỉ số hiệu suất tương ứng với các hệ số chuyển 
tải và các mô men xoắn được sinh ra tại hai cầu. 
Chúng được xác định cụ thể như sau: 
2 2
Normalized_load_transfer
0 0
2 2
0 0
Torque
2 2
max max
0 0
1 1 1
( ) ( )
2
1 1
( ) ( )
1
2 1 1
( ) ( )
T T
f r
T T
f r
T T
f r
f R t dt R t dt
T T
U t dt U t dt
T T
f
U t dt U t dt
T T
 (7) 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 73 (3/2021) 7 
Trong đó Rf;r là các hệ số chuyển tải và Uf;r là 
các mô men xoắn được sinh ra tại cầu trước và cầu 
sau. Uf;rmax được xác định khi bài toán tối ưu tập 
chung duy nhất vào các hệ số chuyển tải (tức là 
giá trị các mô men xoắn khi đó không được xem 
xét trong bài toán tối ưu hóa). Trong trường hợp 
đó, 1 và Normalized_load_transferf f . 
Bằng việc thay đổi giá trị của từ 0 đến 1 thì 
hàm mục tiêu f sẽ được tối ưu theo tương quan 
giữa hai hiệu suất này tương ứng. 
5.2. Công thức của bài toán tối ưu đa mục 
tiêu (MCO) 
Các hàm trọng số được sử dụng với tương quan 
với hệ thống như trong Hình 2, được nêu chi tiết 
trong phần này. Hàm trọng số cho kích thích được 
chọn là 
180
dW
 , giá trị này để giới hạn góc 
đánh lái f đến giá trị được mong đợi lớn nhất. 
Các hàm trọng số Wn1 và Wn2 đặc trưng cho 
nhiễu cảm biến được chọn như: 1 2 0.01n nW W . 
Các trọng số này được chọn là 0.01(m/s2) cho vận 
tốc của góc nghiêng ngang thân xe  và gia tốc 
ngang (Gaspar, et al 2004). Lưu ý rằng có thể lựa 
chọn các bộ lọc thấp khác tùy theo công nghệ và 
dạng của cảm biến. 
Các hàm trọng số Wzi đại diện cho các đầu ra 
hiệu suất (Wz1, Wz2, Wz3, Wz4 và Wz5). Mục đích 
của các hàm trọng số là để giữ giá trị tuyệt đối nhỏ 
nhất của các tín hiệu đầu vào điều khiển, các hệ số 
chuyển tải và gia tốc ngang trên một dải tần số 
mong muốn. Các hàm trọng số này có thể được 
lựa chọn thông qua phương pháp thử, kiểm tra 
bằng kinh nghiệm của người thiết kế. Ở nghiên 
cứu này, các hàm trọng số sẽ được xác định dạng 
hàm trước, sau đó bằng thuật giải di truyền, các hệ 
số của hàm sẽ được lựa chọn tối ưu. 
Các hàm trọng số Wz1 và Wz2 tương ứng với các 
mô men xoắn điều khiển được sinh ra bởi hệ 
thống ổn định ngang chủ động ở cầu trước và cầu 
sau, được chọn là: 
1
1
1
ZW
Z
 ; 2
2
1
ZW
Z
 (8) 
Các hàm trọng số Wz3 và Wz4 tương ứng với các 
hệ số chuyển tải tại cầu trước và cầu sau được 
chọn là: 3
3
1
ZW
Z
 ; 4
4
1
ZW
Z
 (9) 
Hàm trọng số Wz5 đặc trưng cho gia tốc ngang 
được chọn là: 52 535 51
54 55
Z
Z s Z
W Z
Z s Z
 (10) 
Ở đây, hàm trọng số Wz5 tương ứng với một thiết 
kế nhằm tránh hiện tượng lật ngang với tác động của 
người lái xe trong dải tần số lên đến 4 rad/s. Hàm 
trọng số này sẽ trực tiếp giảm thiểu gia tốc ngang khi 
nó đạt đến giá trị giới hạn, để tránh hiện tượng lật. 
Cần lưu ý rằng, các thông số Zij là các hằng số, 
bao gồm: Z1, Z2, Z3, Z4, Z51, Z52, Z53, Z54, Z55. 
Bài toán MCO cho hệ thống ổn định ngang chủ 
động điều khiển H∞ có thể được kí hiệu là: 
 
_ _
1 2 3 4 51 52 53 54 55
min ( ), ( ) :
: [ , , , , , , , , ] |
T
Normalized load transfer Torque
p P
T l u
f p f p f f
P p Z Z Z Z Z Z Z Z Z R p p p
 (11) 
Trong đó f(p) là véc tơ của các mục tiêu, p là 
véc tơ của các thông số hàm trọng số, pl và pu là 
giới hạn dưới và giới hạn trên của các phần tử của 
hàm trọng số. Giới hạn dưới và giới hạn trên của 
các phần tử của hàm trọng số được xác định trong 
Bảng 1. 
Bảng 1. Giới hạn dưới và giới hạn trên của các phần tử của hàm trọng số 
Wz1 Wz2 Wz3 Wz4 Wz5j 
Z1 Z2 Z3 Z4 Z51 Z52 Z53 Z54 Z55 
Giới hạn dưới 50 50 0.1 0.1 0.5 0.00033 1 1 0.001 
Giới hạn trên 300000 300000 10 10 100 1 500 1000 2 
 KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 73 (3/2021) 8 
6. KẾT QUẢ MÔ PHỎNG VÀ ĐÁNH GIÁ 
6.1. Kết quả tối ưu hóa hàm trọng số 
Nhờ vào phương pháp thuật giải di truyền, việc 
tính toán giá trị các phần tử hàm trọng số sẽ dừng lại 
khi bài toán tối ưu đa mục tiêu toàn phần được thực 
hiện. Bảng 2 tổng hợp các giá trị của các biến Zi, Z5j 
trong 5 trường hợp cho [1;0.85;0.65;0.5;0] . 
Khi 1 , điều đó có nghĩa là 
Normalized_load_transferf f , bài toán tối ưu chỉ tập 
chung vào các hệ số chuyển tải và khi 0 , điều 
đó có nghĩa là Torquef f , bài toán tối ưu chỉ tập 
chung vào các mô men xoắn được sinh ra bởi cơ cấu 
chấp hành. 
Bảng 2. Các kết quả tối ưu các hàm trọng số của hệ thống ổn định ngang chủ động điều khiển H∞ 
Wz1 Wz2 Wz3 Wz4 Wz5j Các bộ điều 
khiển Z1 Z2 Z3 Z4 Z51 Z52 Z53 Z54 Z55 
SSSC2016 150000 200000 1 1 1 0.0005 50 100 0.01 
1 258762.34 259996.91 0.91 0.64 0.97 0.46 392.54 801.38 0.22 
0.85 273598.36 295104.17 0.45 0.26 1.17 0.80 334.15 968.50 0.16 
0.65 112322.78 110837.28 0.72 0.75 0.63 0.54 139.23 97.46 0.02 
0.5 166902.22 196036.53 1.09 0.92 0.97 0.0005 54.19 116.64 0.01 
0 50 50 1.59 0.83 0.50 0.43 1 683.05 0.024 
Hình 3 biểu diễn mối quan hệ đối nghịch 
giữa chỉ số hiệu xuất về hệ số chuyển tải và mô 
men xoắn với một số điểm của đường biên giới 
tối ưu Pareto, tương ứng với các giá trị khác 
nhau của α trong khoảng [0;1]. Đối với α=0, 
Torquef là cực tiểu và ngược lại đối với α=1, 
Normalized_load_transferf là cực tiểu. 
Hình 3. Đường biên giới tối ưu Pareto của hệ 
thống ổn định ngang chủ động điều khiển H∞ 
6.2. Đánh giá kết quả tối ưu trên miền tần số 
Trong phần này tác giả so sánh hàm truyền 
biên độ của các hệ số chuyển tải ở hai cầu dưới tác 
động từ góc đánh lái khi vận tốc chuyển động của 
ô tô V được giữa cố định ở 70 Km/h. 
Hình 4 và 5 cho thấy độ lớn các hàm truyền 
biên độ của các hệ số chuyển tải ở hai cầu Rf,r. 
Chúng chỉ ra rằng trong trường hợp 
[1;0.85;0.65] , các bộ điều khiển hệ thống 
ổn định ngang chủ động H∞ giảm nhiều các hệ 
số chuyển tải so với trong trường hợp ô tô sử 
dụng thanh ổn định ngang bị động và trường 
hợp bài báo trước đó (Vu, et al 2016) khi các 
hàm trọng số được lựa chọn bởi các thử nghiệm. 
Điều này thỏa mãn mục tiêu điều khiển trong 
việc giảm hệ số chuyển tải trong vùng tần số 
dưới 4 rad/s (Gaspar, et al 2004). 
Hình 4. Hàm truyền biên độ từ góc đánh lái đến 
hệ số chuyển tải ở cầu trước (Rf ) 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 73 (3/2021) 9 
Hình 5. Hàm truyền biên độ từ góc đánh lái đến 
hệ số chuyển tải ở cầu sau (Rr ) 
7. KẾT LUẬN 
Bài báo này đã đề xuất áp dụng phương pháp 
thuật giải di truyền cho hệ thống ổn định ngang 
chủ động trên ô tô tải để tối ưu hóa các hàm trọng 
số của bộ điều khiển bền vững H∞. Các mục tiêu 
đối nghịch giữa các hệ số chuyển tải và mô men 
xoắn được tạo ra bởi cơ cấp chấp hành được xử lý 
chỉ bằng một thông số điều chỉnh cấp cao duy 
nhất, đây chính là một ưu thế lớn để giải quyết các 
vấn đề điều khiển đa mục tiêu. Các kết quả mô 
phỏng trên miền tần số đã cho thấy hiệu quả của 
phương pháp thuật giải di truyền trong việc tìm 
kiếm một bộ điều khiển phù hợp để đáp ứng một 
số chỉ tiêu hiệu suất của điều khiển bền vững. Đây 
là cách tiếp cận hoàn toàn mới trong việc nghiên 
cứu hệ thống ổn định ngang chủ động trên ô tô. 
Mặc dù cấu trúc các hàm trọng số đã được định 
dạng sẵn tuy nhiên phương pháp thuật giải di 
truyền cũng có thể áp dụng với các cấu trúc phức 
tạp hơn nhưng vẫn phụ thuộc vào kinh nghiệm của 
người thiết kế để bài toán đạt được kết quả và tốc 
độ tính toán hợp lý. Việc áp dụng phương pháp đã 
được đề xuất cho hệ có thông số thay đổi LPV có 
thể đem lại kết quả tốt hơn trong tương lai. 
TÀI LIỆU THAM KHẢO 
Alfaro Cid E., Mc Gookin E.W., and Murray-Smith D.J, (2008), Optimisation of the weighting functions 
of an H∞ controller using genetic algorithms and structured genetic algorithms, International Journal 
of Systems Science, p.335-347. 
Davis L.D, (1991), Handbook of genetic algorithms, Van Nostrand Reinhold. 
Do L., Soualmi B., Lozoya S., Sename O., Dugard L., Ramirez Mendoza, (2010), Optimization of 
weighting function selection for H∞ control of semi-active suspensions, 12
th Conference on vehicle 
system dynamics, identification and anomalies, Budapest, Hungary. 
Gaspar P., Bokor J., and Szaszi I, (2004), The design of a combined control structure to prevent the 
rollver of heavy vehicles, European Journal of Control, p.148-162. 
Gaspar P., Bokor J., and Szaszi I, (2005), Reconfigurable control structure to prevent the rollover of 
heavy vehicles, Control Engineering Practice, p.699-711. 
Goldberg D, (1989), Genetic Algorithms in Searching Optimisation and Machine Learning, Addison-
Wesley Longman. 
Holland H.J, (1975), Adaptation in natural and artificial systems, an introductory analysis with 
application to biology, control and artificial intelligence, The university of Michigan Press. 
Kitsios I., and Pimenides T., (2002), H∞ controller design for a distillation column using genetic 
algorithms, Mathematics and Computers in Simulation. 
Vu V.T., Sename O., Dugard L., and Gaspar P, (2016), Active anti-roll bar control using electronic 
servo-valve hydraulic damper on single unit heavy vehicle, IFAC Symposium on Advances in 
Automotive Control - 8th AAC 2016, Sweden. 
Vu V.T., Sename O., Dugard L., and Gaspar P, (2016), H∞ active anti-roll bar control to prevent 
rollover of heavy vehicles: a robustness analysis, IFAC Symposium on System Structure and Control 
- 6th SSSC 2016, Turkey. 
 KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 73 (3/2021) 10 
Abstract: 
OPTIMAL SELECTION OF WEIGHTING FUNCTIONS FOR H∞ 
ACTIVE ANTI-ROLL BAR CONTROL SYSTEM ON TRUCKS 
The objective of an active anti-roll bar system of trucks is to maximize roll stability to prevent rollover 
in dangerous cases. However, such a performance objective must be balanced with the energy 
consumption of the anti-roll bar system, which is not a trivial task. In this paper, Genetic Algorithms 
(GAs) are proposed to find optimal weighting functions for the H∞ control synthesis of the active anti-
roll bar system. Such a general procedure is applied to the case of active anti-roll bar control system on 
trucks. Thanks to GAs, the conflicting objectives between roll stability and torques generated are 
handled using one high level parameter only. The multi-criterion optimization solution is illustrated via 
the Pareto frontier. Simulations, performed in the frequency domain, emphasize the efficiency of the 
proposed method. 
Keywords: H∞ control, Genetic Algorithms, Truck, Active anti-roll bar system, Rollover, Roll stability. 
Ngày nhận bài: 05/12/2020 
Ngày chấp nhận đăng: 04/02/2021