Nghiên cứu sự biến dạng của phoi khi mô phỏng quá trình gia công hợp kim nhôm A6061

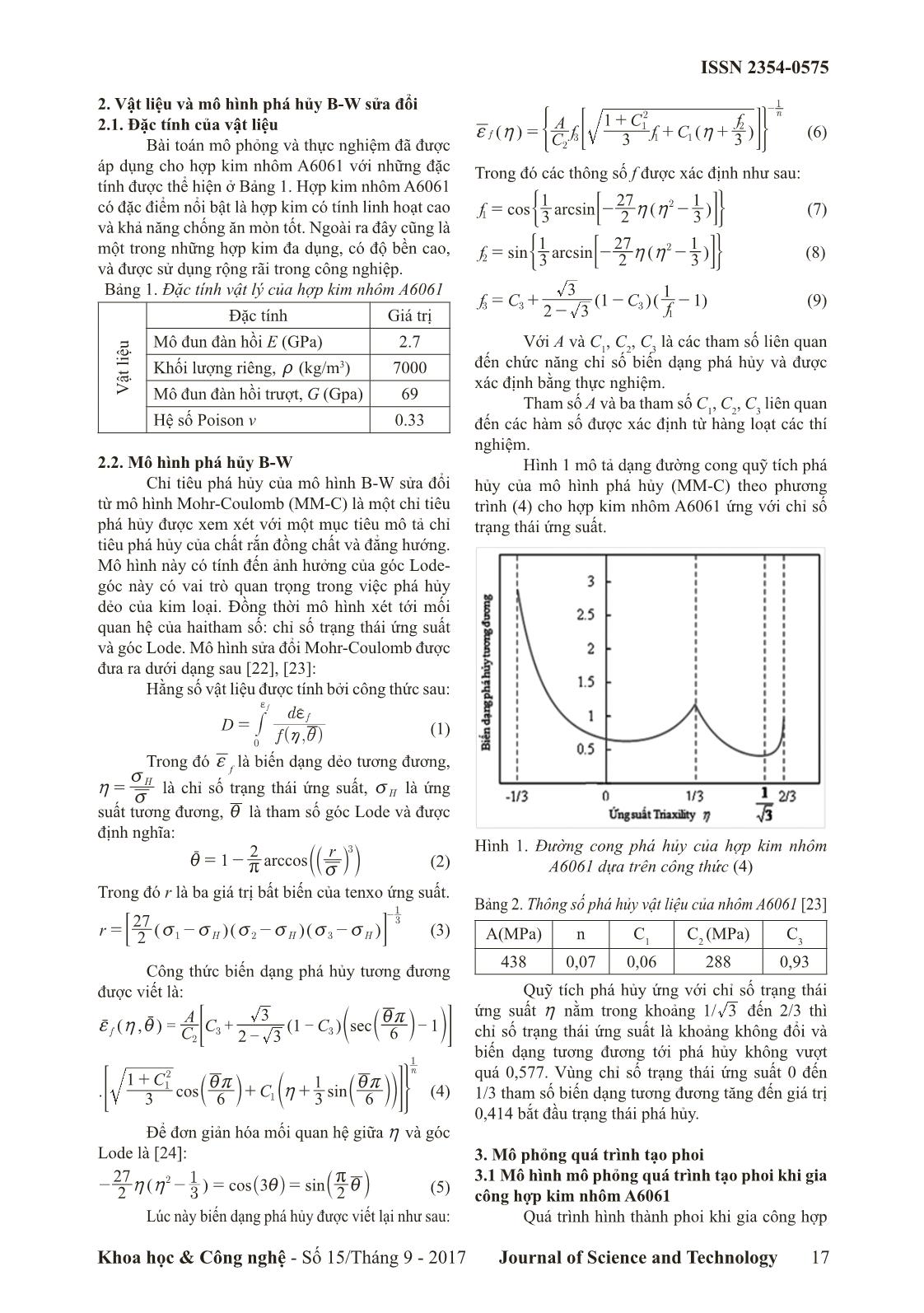
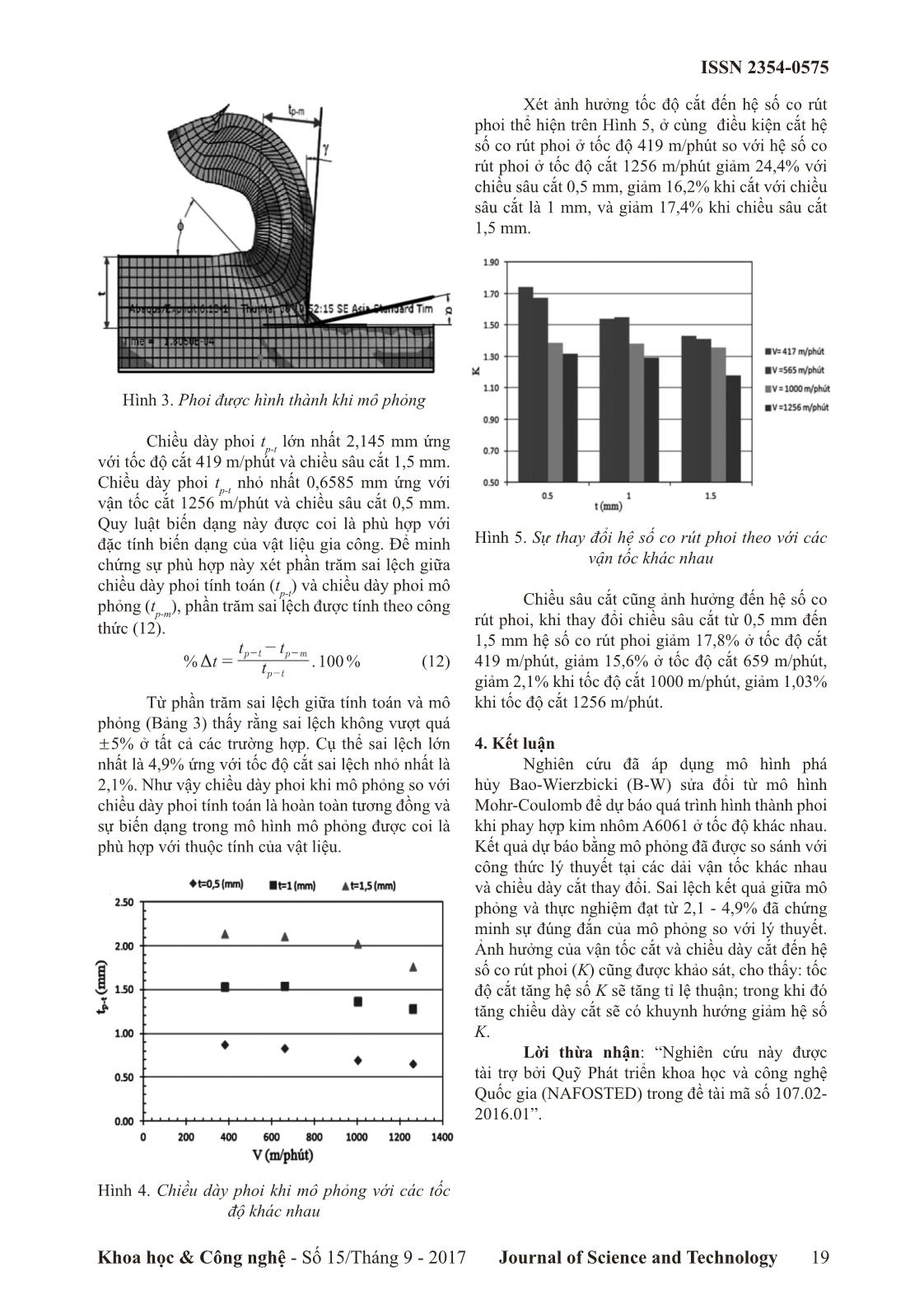
 khả năng chống ăn mòn tốt. Ngoài ra đây cũng là 
một trong những hợp kim đa dụng, có độ bền cao, 
và được sử dụng rộng rãi trong công nghiệp. 
Bảng 1. Đặc tính vật lý của hợp kim nhôm A6061
V
ật
 li
ệu
Đặc tính Giá trị
Mô đun đàn hồi E (GPa) 2.7
Khối lượng riêng, t (kg/m3) 7000
Mô đun đàn hồi trượt, G (Gpa) 69
Hệ số Poison v 0.33
2.2. Mô hình phá hủy B-W
Chỉ tiêu phá hủy của mô hình B-W sửa đổi 
từ mô hình Mohr-Coulomb (MM-C) là một chỉ tiêu 
phá hủy được xem xét với một mục tiêu mô tả chỉ 
tiêu phá hủy của chất rắn đồng chất và đẳng hướng. 
Mô hình này có tính đến ảnh hưởng của góc Lode- 
góc này có vai trò quan trọng trong việc phá hủy 
dẻo của kim loại. Đồng thời mô hình xét tới mối 
quan hệ của haitham số: chỉ số trạng thái ứng suất 
và góc Lode. Mô hình sửa đổi Mohr-Coulomb được 
đưa ra dưới dạng sau [22], [23]: 
Hằng số vật liệu được tính bởi công thức sau:
D
( , )f
d
0
f
f
=
f
f
h i
r
#
(1)
Trong đó f f là biến dạng dẻo tương đương, 
Hh
v
v
= là chỉ số trạng thái ứng suất, Hv là ứng 
suất tương đương, i là tham số góc Lode và được 
định nghĩa:
arccos r1 2
3
ri v
= -r ab k l (2)
Trong đó r là ba giá trị bất biến của tenxo ứng suất. 
( ) ( ) ( )r 2
27
H H H1 2 3
3
1
v v v v v v= - - -
-; E (3)
Công thức biến dạng phá hủy tương đương 
được viết là:
( , ) ( ) secC
A C C2 3
3 1 6 1f 2 3 3f h i
ir
= +
-
- -r r bd l n= G
. cos sin
C
C3
1
6 3
1
6
n
1
2
1
1
ir h ir
+
+ +b bdl ln> H4 (4)
Để đơn giản hóa mối quan hệ giữa h và góc 
Lode là [24]:
( ) cos sin2
27 3 2
2
3
1 rh h i i- - = =_ ai k (5)
Lúc này biến dạng phá hủy được viết lại như sau:
( ) ( )C
A f
C
f C
f
3
1
3f
n
2
3
1
2
1 1
2
1
f h h=
+
+ +
-= G* 4 (6)
Trong đó các thông số f được xác định như sau:
cos arcsin ( )f 3
1
2
27
3
1
1
2h h= - -; E( 2 (7) 
sin arcsin ( )f 3
1
2
27
3
1
2
2h h= - -; E( 2 (8)
( ) ( )f C C f2 3
3 1 1 13 3 3
1
= +
-
- - (9)
Với A và C1, C2, C3 là các tham số liên quan 
đến chức năng chỉ số biến dạng phá hủy và được 
xác định bằng thực nghiệm. 
Tham số A và ba tham số C1, C2, C3 liên quan 
đến các hàm số được xác định từ hàng loạt các thí 
nghiệm. 
Hình 1 mô tả dạng đường cong quỹ tích phá 
hủy của mô hình phá hủy (MM-C) theo phương 
trình (4) cho hợp kim nhôm A6061 ứng với chỉ số 
trạng thái ứng suất.
Hình 1. Đường cong phá hủy của hợp kim nhôm 
A6061 dựa trên công thức (4)
Bảng 2. Thông số phá hủy vật liệu của nhôm A6061 [23]
A(MPa) n C1 C2 (MPa) C3
438 0,07 0,06 288 0,93
Quỹ tích phá hủy ứng với chỉ số trạng thái 
ứng suất h nằm trong khoảng /1 3 đến 2/3 thì 
chỉ số trạng thái ứng suất là khoảng không đổi và 
biến dạng tương đương tới phá hủy không vượt 
quá 0,577. Vùng chỉ số trạng thái ứng suất 0 đến 
1/3 tham số biến dạng tương đương tăng đến giá trị 
0,414 bắt đầu trạng thái phá hủy. 
3. Mô phỏng quá trình tạo phoi 
3.1 Mô hình mô phỏng quá trình tạo phoi khi gia 
công hợp kim nhôm A6061
Quá trình hình thành phoi khi gia công hợp 
ISSN 2354-0575
Journal of Science and Technology18 Khoa học & Công nghệ - Số 15/Tháng 9 - 2017
kim nhôm A6061 được mô phỏng bằng phần mềm 
thương mại Abaqus/Explicit 6.13. Điều kiện biên và 
phần tử lưới được thiết lập cho mô hình mô phỏng 
2D được thể hiện trên Hình 2. Trong đó phôi cắt 
được mô hình hóa bằng 4 nút song tuyến (CPE4R), 
dụng cụ cắt được coi là phần tử cứng.
Hình 2. Mô hình phần tử hữu hạn trong quá trình cắt
Phôi mô phỏng được phân chia thành 4 phần 
được ký hiệu như sau: Phần 1 là dụng cụ cắt, phần 
2 là chiều dày cắt, phần 3 là phần phá hủy, phần 4 
là phôi nền. Phần phá hủy được mô hình hóa bằng 
ba lớp phần tử với tổng chiều dày lớn hơn bán kính 
dụng cụ cắt. Lớp phoi được hình thành, biến dạng 
chủ yếu từ lớp phoi chưa cắt (lớp chiều dày cắt) và 
một phần được sinh ra từ các phần tử trong lớp phá 
hủy, phần còn lại sẽ bị phá hủy hoặc bị xóa. Mô 
phỏng phoi hình thành ở tốc độ cắt 1000 m/phút, 
chiều dày cắt t có thể được thay đổi với góc trước 
và góc sau của dụng cụ cắt tương ứng là 5o và 5o 
như Hình 2.
3.2. Sự biến dạng của phoi trong quá trình hình 
thành
Phoi hình thành sau khi gia công có kích 
thước thay đổi so với kích thước lớp phoi ban đầu. 
Gọi chiều dày phoi được hình thành khi mô phỏng 
là t
p-m
 như trên Hình 4.20. Sau khi mô phỏng quá 
trình hình thành phoi, xác định được hệ số co rút 
phoi và chiều dày phoi khi mô phỏng thông theo 
công thức (10). 
K t
tp m
=
-
(10)
Chiều dày phoi còn được tính toán (t
p-t 
) theo 
góc biến dạng z của Merchant’s [25] chiều dày 
phoi tính toán thay đổi góc biến dạng, tốc độ cắt 
và chiều sâu cắt khác nhau theo công thức (10). Và 
được tính theo công thức (11).
. sin tan
cos
t tp t a z
c
= +- d n
(11)
Trong đó: c là góc trước của dao, z là góc biến 
dạng được xác định từ miền bắt đầu xảy ra biến 
dạng so với mũi dụng cụ cắt như Hình 3.
Chiều dày phoi mô phỏng được đo trên mặt 
phẳng vuông góc với mặt trước của dụng cụ cắt. Mô 
phỏng xác định hệ số co rút phoi, chiều dày phoi ở 
các tốc độ cắt 419, 565, 1000, 1256 m/phút và chiều 
sâu cắt tương ứng 0,5; 1,0 và 1,5 mm. Kết quả tính 
toán và mô phỏng được cho trên Bảng 3.
Từ kết quả trên Bảng 3 và Hình 4 cho thấy 
xu thế ảnh hưởng của chiều dày phoi tính toán ứng 
chiều sâu cắt và vận tốc cắt khác nhau. Khi tăng tốc 
độ cắt thì chiều dày phoi giảm và khi tăng chiều sâu 
cắt thì chiều dày phoi lại tăng.
Bảng 3. Chiều dày phoi trong quá trình mô phỏng
V (m/phút) t (mm) t
pm
 (mm) z (o) K tp-t (mm) % Tt
419
0,5 0,870 32 1,74 0,841 0,034
1,0 1,540 33 1,54 1,62 0,049
1,5 2,145 34,5 1,43 2,23 0,038
565
0,5 0,835 33 1,67 0,812 0,028
1,0 1,550 34 1,55 1,56 0,006
1,5 2,115 35,5 1,41 2,223 0,049
1000
0,5 0,693 36,5 1,39 0,716 0,033
1,0 1,381 39 1,38 1,317 0,049
1,5 2,034 39,5 1,36 1,943 0,047
1256
0,5 0,658 40 1,32 0,637 0,033
1,0 1,414 37,5 1,35 1,233 0,021
1,5 2,052 38,5 1,35 1,79 0,021
ISSN 2354-0575
Khoa học & Công nghệ - Số 15/Tháng 9 - 2017 Journal of Science and Technology 19
Hình 3. Phoi được hình thành khi mô phỏng
Chiều dày phoi t
p-t
 lớn nhất 2,145 mm ứng 
với tốc độ cắt 419 m/phút và chiều sâu cắt 1,5 mm. 
Chiều dày phoi t
p-t
 nhỏ nhất 0,6585 mm ứng với 
vận tốc cắt 1256 m/phút và chiều sâu cắt 0,5 mm. 
Quy luật biến dạng này được coi là phù hợp với 
đặc tính biến dạng của vật liệu gia công. Để minh 
chứng sự phù hợp này xét phần trăm sai lệch giữa 
chiều dày phoi tính toán (t
p-t
) và chiều dày phoi mô 
phỏng (t
p-m
), phần trăm sai lệch được tính theo công 
thức (12).
% . %t t
t t
100
p t
p t p m
D =
-
-
- -
 (12)
Từ phần trăm sai lệch giữa tính toán và mô 
phỏng (Bảng 3) thấy rằng sai lệch không vượt quá 
!5% ở tất cả các trường hợp. Cụ thể sai lệch lớn 
nhất là 4,9% ứng với tốc độ cắt sai lệch nhỏ nhất là 
2,1%. Như vậy chiều dày phoi khi mô phỏng so với 
chiều dày phoi tính toán là hoàn toàn tương đồng và 
sự biến dạng trong mô hình mô phỏng được coi là 
phù hợp với thuộc tính của vật liệu.
Hình 4. Chiều dày phoi khi mô phỏng với các tốc 
độ khác nhau
Xét ảnh hưởng tốc độ cắt đến hệ số co rút 
phoi thể hiện trên Hình 5, ở cùng điều kiện cắt hệ 
số co rút phoi ở tốc độ 419 m/phút so với hệ số co 
rút phoi ở tốc độ cắt 1256 m/phút giảm 24,4% với 
chiều sâu cắt 0,5 mm, giảm 16,2% khi cắt với chiều 
sâu cắt là 1 mm, và giảm 17,4% khi chiều sâu cắt 
1,5 mm.
Hình 5. Sự thay đổi hệ số co rút phoi theo với các 
vận tốc khác nhau
Chiều sâu cắt cũng ảnh hưởng đến hệ số co 
rút phoi, khi thay đổi chiều sâu cắt từ 0,5 mm đến 
1,5 mm hệ số co rút phoi giảm 17,8% ở tốc độ cắt 
419 m/phút, giảm 15,6% ở tốc độ cắt 659 m/phút, 
giảm 2,1% khi tốc độ cắt 1000 m/phút, giảm 1,03% 
khi tốc độ cắt 1256 m/phút.
4. Kết luận
Nghiên cứu đã áp dụng mô hình phá 
hủy Bao-Wierzbicki (B-W) sửa đổi từ mô hình 
Mohr-Coulomb để dự báo quá trình hình thành phoi 
khi phay hợp kim nhôm A6061 ở tốc độ khác nhau. 
Kết quả dự báo bằng mô phỏng đã được so sánh với 
công thức lý thuyết tại các dải vận tốc khác nhau 
và chiều dày cắt thay đổi. Sai lệch kết quả giữa mô 
phỏng và thực nghiệm đạt từ 2,1 - 4,9% đã chứng 
minh sự đúng đắn của mô phỏng so với lý thuyết. 
Ảnh hưởng của vận tốc cắt và chiều dày cắt đến hệ 
số co rút phoi (K) cũng được khảo sát, cho thấy: tốc 
độ cắt tăng hệ số K sẽ tăng tỉ lệ thuận; trong khi đó 
tăng chiều dày cắt sẽ có khuynh hướng giảm hệ số 
K.
Lời thừa nhận: “Nghiên cứu này được 
tài trợ bởi Quỹ Phát triển khoa học và công nghệ 
Quốc gia (NAFOSTED) trong đề tài mã số 107.02-
2016.01”.
ISSN 2354-0575
Journal of Science and Technology20 Khoa học & Công nghệ - Số 15/Tháng 9 - 2017
Tài liệu tham khảo
[1]. T. Data, “Fracture Characteristics of Three Matals Subjected to Various Strains, Strain Rates, 
Temperature and Perssures,” Eng. Mech., vol. 21, no. I, 1985.
[2]. M. S. Swan, “Incorporation of a General Strain-to - failure Fracture Criterion into a Stress 
based Plasticty Model through a Time to Failure by,” Thesis Mech. Eng. - Univ. Utah, USA., no. 
May, 2012.
[3]. O. Article, “On Predicting Chip Morphology and Phase Transformation in Hard Machining,” 
Int Adv Manuf Technol, pp. 645–654, 2006.
[4]. J. Shi and C. R. Liu, “Flow Stress Property of a Hardened Steel at Elevated Ttemperatures with 
Tempering e ect,” Int. J. Mech. Sci., vol. 46, pp. 891–906, 2004.
[5]. M. L. Wilkins, R. D. Streit, and J. E. Reaugh, “Cumulative-Strain-Damage Model of Ductile 
Fracture: Simulation and Prediction of Engineering Fracture Tests,” Lawrence Livermore Natl. 
Lab., pp. 1–68, 1980.
[6]. D. J. L. M.G.Cockcroft, “Ductility and the Workability of Metals .pdf.” p. J Inst Metals, 1968.
[7]. E. Ceretti, M. Lucchi, and T. Altan, “FEM Simulation of Orthogonal Cutting: Serrated Chip 
Formation,” Juornal Mater. Process. Technol., vol. 95, pp. 17–26, 1999.
[8]. J. Lorentzon, N. Järvstråt, and B. L. Josefson, “Journal of Materials Processing Technology 
Modelling Chip Formation of Alloy 718,” J. Mater. Process. Technol., vol. 209, pp. 4645–4653, 2009.
[9]. A. Gilioli, A. Manes, M. Giglio, and T. Wierzbicki, “Predicting Ballistic Impact Failure of Alu-
minium 6061-T6 with the Rate-independent Bao-Wierzbicki Fracture Model,” International Journal 
of Impact Engineering, vol. 76. pp. 207–220, 2015.
[10]. M. Giglio, A. Manes, and F. Viganò, “Numerical Simulation of the Slant Fracture of a 
Helicopter’s Rotor Hub with Ductile Damage Failure Criteria,” Fatigue Fract. Eng. Mater. Struct., 
vol. 35, no. 4, pp. 317–327, 2012.
[11]. R. Stringfellow and C. Paetsch, “Modeling Material Failure During Cab Car End Frame 
Impact,” in 2009 Joint Rail Conference, 2009, pp. 183–192.
[12]. X. Teng and T. Wierzbicki, “Effect of Fracture Criteria on High Velocity Perforation of Thin 
Beams.,” Int. J. Comput. Methods, vol. 1, no. 1, pp. 171–200, Jun. 2004.
[13]. H. Z. Li and J. Wang, “A Cutting Fforces Model for Milling Inconel 718 Alloy based on A 
Material Constitutive Law,” Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci., vol. 227, no. 8, pp. 
1761–1775, 2013.
[14]. Y. Chen, H. Li, and J. Wang, “Analytical Modelling of Cutting Forces in Near-orthogonal 
Cutting of Titanium Alloy Ti6Al4V,” Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci., vol. 229, no. 
6, pp. 1122–1133, 2015.
[15]. M. H. Ali, B. a. Khidhir, M. N. M. Ansari, and B. Mohamed, “FEM to Predict the Effect of 
Feed Rate on Surface Roughness with Cutting Force during Face Milling of Titanium Alloy,” HBRC 
J., vol. 9, no. 3, pp. 263–269, 2013.
[16]. X. Cui, B. Zhao, F. Jiao, and J. Zheng, “Chip Formation and its Effects on Cutting Force, Tool 
Temperature, Tool Stress, and Cutting Edge Wear in High- and Ultra-high-speed Milling,” Int. J. 
Adv. Manuf. Technol., vol. 83, no. 1–4, pp. 55–65, 2016.
[17]. A. Davoudinejad, E. Chiappini, S. Tirelli, M. Annoni, and M. Strano, “Finite Element Simula-
tion and Validation of Chip Formation and Cutting Forces in Dry and Cryogenic Cutting of Ti-6Al-
4V,” Procedia Manuf., vol. 1, pp. 728–739, 2015.
[18]. D. Xu, P. Feng, W. Li, and Y. Ma, “An Improved Material Constitutive Model for Simulation of 
High-speed Cutting of 6061-T6 Aluminum Alloy with High Accuracy,” Int. J. Adv. Manuf. Technol., 
vol. 79, no. 5–8, pp. 1043–1053, 2015.
[19]. M. Bäker, “Finite Element Simulation of High-speed Cutting Forces,” J. Mater. Process. 
Technol., vol. 176, no. 1–3, pp. 117–126, 2006.
[20]. J. P. Davim, C. Maranhão, M. J. Jackson, G. Cabral, and J. Grácio, “FEM Snalysis in High Speed 
Machining of Aluminium Alloy (Al7075-0) using Polycrystalline Diamond (PCD) and Cemented 
Carbide (K10) Cutting Tools,” Int. J. Adv. Manuf. Technol., vol. 39, no. 11–12, pp. 1093–1100, 2008.
[21]. M. H. Ali, B. a. Khidhir, B. Mohamed, and a. a. Oshkour, “Prediction of High Cutting Speed 
Parameters for Ti-6Al-4V by Using Finite Element Modeling,” Int. J. Model. Optim., vol. 2, no. 1, 
pp. 31–35, 2012.
ISSN 2354-0575
Khoa học & Công nghệ - Số 15/Tháng 9 - 2017 Journal of Science and Technology 21
[22]. Y. Bai and T. Wierzbicki, “Application of extended Mohr-Coulomb Criterion to Ductile 
Fracture,” Int. J. Fract., vol. 161, no. 1, pp. 1–20, 2010.
[23]. Y. Li, T. Wierzbicki, M. A. Sutton, J. Yan, and X. Deng, “Mixed Mode Stable Tearing of Thin 
Sheet AI 6061-T6 Specimens: Experimental Measurements and Finite Element Simulations using a 
Modified Mohr-Coulomb Fracture Criterion,” Int. J. Fract., vol. 168, no. 1, pp. 53–71, 2011.
[24]. A. M. Beese, M. Luo, Y. Li, Y. Bai, and T. Wierzbicki, “Partially Coupled Anisotropic Fracture 
Model for Aluminum Sheets,” Eng. Fract. Mech., vol. 77, no. 7, pp. 1128–1152, 2010.
[25]. M. E. Merchant, “Mechanics of the Metal Cutting Process. I. Orthogonal Cutting and a Type 
2 Chip,” J. Appl. Phys., vol. 16, no. 5, pp. 267–275, 1945.
SIMULATION STUDY TO VERIFY THE EFFECT OF CUTTING PARAMETERS ON CHIP 
SHINKEGE COEFICIENT DURING MACHINING PROCESS OF ALUMINUM ALLOY
Abstract:
This paper presents a numerical study onparameters of thechip producedin high-speed milling of 
aluminum alloy considering the effect of cutting depth and speed.First, a finite element model was created 
by the ABAQUS / Explicit finite element simulation software, based onthe Bao-Wierzbicki (B-W) fracture 
model with modified Mohr-Coulomb criterion. The model verification was made by comparing the simulated 
chip thickness to that obtained by theoretical formulae. Then, the effect of cutting depth and speed on the 
chip thickness, chip shrinkage coefficient and shear angle of chip were investigated. The simulation results 
showed that the chip thickness reduced with increasing cutting speed. In addition, increasing cutting speed 
or cutting depth reduces the chip shrinkage coefficient, but increases the the shear angle of chip.
Keywords: Chip shrinkage coefficient, the Bao-Wierzbicki fracture model, modified Mohr-Coulomb criteria, 
A6061 aluminum alloy, simulation of the cutting process.