Hiệu năng đường xuống trong hệ thống đa truy nhập phi trực giao sử dụng tỷ số Log-Likelihood

c và Công nghệ – Khoa học Tự nhiên, 4(3):621-632
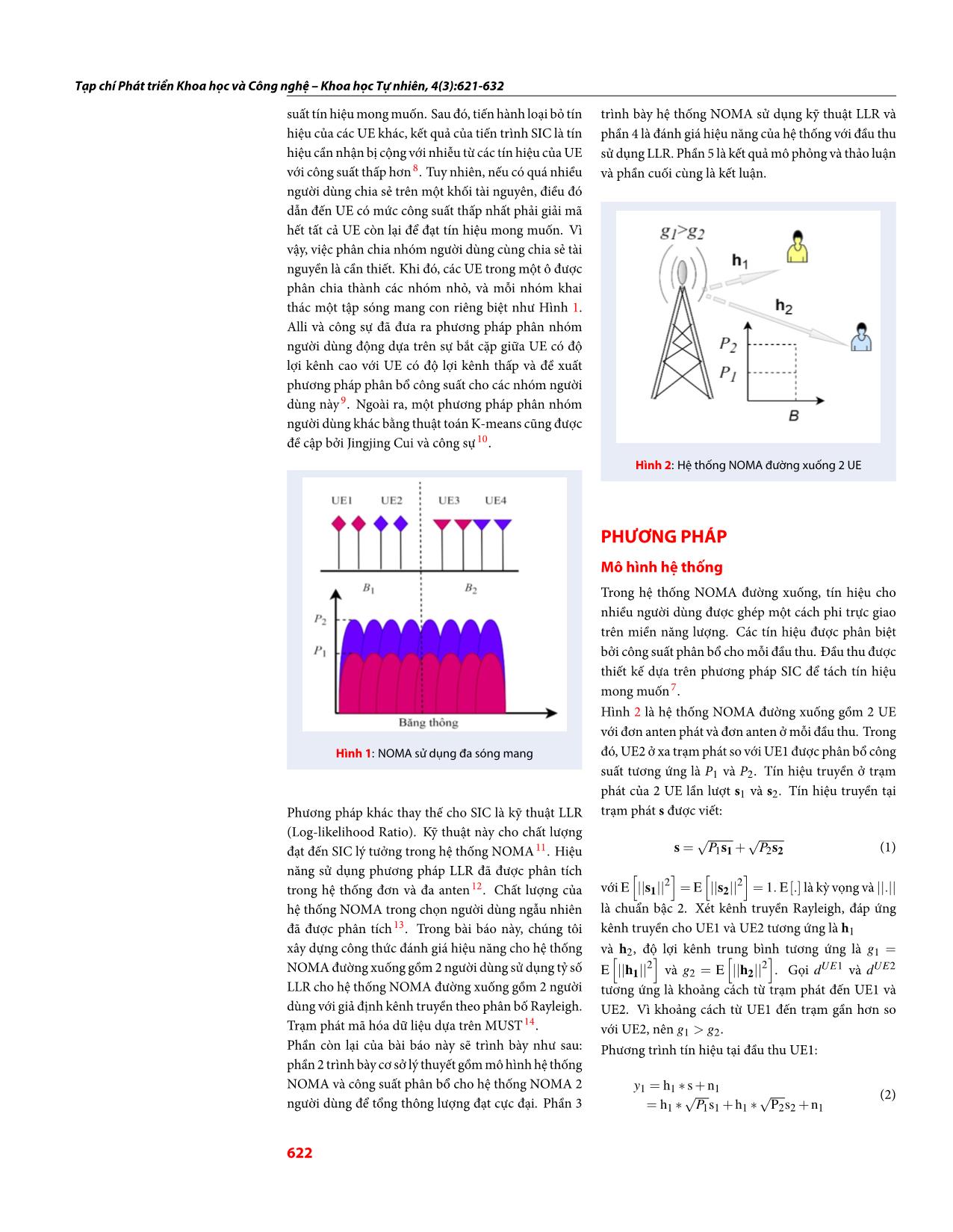
 Hình 4: Điều chế theo MUST loại 2
 Hình 5: Mô hình đầu phát của hệ thống NOMA 2 người dùng
 626
Tạp chí Phát triển Khoa học và Công nghệ – Khoa học Tự nhiên, 4(3):621-632
 Hình 6: Sơ đồ tách tín hiệu dựa trên LLR
 (27) và (29), giải LLR(b1) < 0, điều kiện của nhiễu khoảng cách tối tiểu tới năng lượng trung bình của ký
 khi nhận sai bit khi: hiệu, tỉ lệ lỗi bit được xác định:
 ( √ )
 2
 N2kI > d1 (30) 1 G2d1 /N0
 P | − ≈ 1 − (34)
 b1 S1= d1 2
 2 1 + G2d1 /N0
 Khi đó, Pb1|S1=−d1 được viết lại:
 Một cách tính tương tự cho Pb1|S1=−d2 . Từ (29), với
 P | − = Pr{N > d } (31) ∗ ∗
 b1 S1= d1 2kI 1 S = {−d , −d } và S = {d , d }. Xét lần lượt
 { } αI 1 2 βI 1 2
 S∗ S∗ S = −d
 N2k H2kI trường hợp của αI và βI cùng với 1 2. Tỉ lệ
 N = Re = 2 2 N . Theo giả thiết
 2kI H2k H +H 2kI
 2kI 2kQ lỗi bit cho trường hợp này như sau:
 N ∼ CN( ,N ) N ∼
 2(k ) 0 0 , nhiễu trên trục đồng( pha là 2)kI
 N 1 N0 { }
 N 0, .Do đó, nhiễu là N ∼ N 0, và Pb |S =−d = Pr N2kI > d2
 2 2kI ||H ||2 2 1 1 1 ( √ )
 2k 2
 hàm mật độ là 1 G2d /N0 (35)
 ≈ 1 − 2
 ( ( ) ) 2 1 + G d2/N
 || || 2 2 2 0
 √H2k −|| ||2 √n
 fN2kI (n) = exp H2k
 N0π N0 Dựa trên tính đối xứng của giản đồ chòm sao giữa
 các tập điểm với SI = d1 và SI = −d1, SI = d2 và
 Phương trình (31) được khai triển như sau: −
 SI = d2. Ta xác định được Pb |S =d = Pb |S =−d ,
 ∫ 1 1 1 1 1 1
 +∞ và P | = P | − .
 Pr (N > d ) = f (n)dn b1 S1=d2 b1 S1= d2
 2kI 1 d1 √N2kI 
 Từ phương trình (26), xác suất lỗi bit thứ 1:
 2d2 ||H ||2 (32)
 = Q 1 2k 
 N P ≈
 0 b1( √ √ )
 2 2
 1 G2d1 /N0 G2d2 /N0 (36)
 H ∼ 2 − −
 với (Q(.)[ là hàm]) Q. Từ giải thiết[ 2k ] 4 1 + G d2/N 1 + G d2/N
 2 2 2 1 0 2 2 0
 CN 0,E ||H2k|| , và đặt G2 = E ||H2k||
 2 Đồng thời, giản đồ chòm sao Hình 4 cho thấy Pb =
 là độ lợi kênh trung bình của UE2, ||H2k|| tuân theo 1
 P . Xác suất lỗi bit của UE2:
 phân bố kênh Rayleigh, hàm mật độ xác suất là b2
 ( ) ( )
 1 1 1
 − P_UE2 = Pb1 + Pb2
 f|| ||2 (x) = exp x (√ 2 √ )
 H2k G G
 2 2 G d2/N G d2/N (37)
 ≈ 1 2 1 0 − 2 2 0
 Xác suất P | − được viết: 2 2
 b1 S1= d1 4 1 + G2d1 /N0 1 + G2d2 /N0
  
 √ 1
 2 −
 ∫ ∞ 2d x 1 x Hiệu năng người dùng ở gần trạm gốc UE1
 +  1  G2 (33)
 Pb1|S1=−d1 = 0 Q e dx
 N0 G2 Hai bit tín hiệu của UE1 được ghép vào một ký tự
 truyền dẫn là b3 và b4. Xác suất lỗi bit của UE1 được
 Dựa trên(√ xấp) xỉ cho việc tính tích phân trên cho xác định:
 α Q β x trong 15, với α là số điểm lân cận gần
 M M M 1 ( )
 nhất trong chòm sao, và β là hằng số liên quan đến P_UE1 = Pb3 + Pb4 (38)
 M 2
 627
Tạp chí Phát triển Khoa học và Công nghệ – Khoa học Tự nhiên, 4(3):621-632
 Gọi SI là thành phần đồng pha của bit thứ 3, người KẾT QUẢ VÀ THẢO LUẬN
 dùng thứ 1 và sóng mang thứ k, xác suất lỗi của bit
 Thông số mô phỏng
 b3:
 ( ) Tham số mô phỏng của bài viết dựa trên chuẩn
 17
 1 P | − + P | − LTE/LTE Advance như Bảng 1. UE1 gần trạm phát
 P = b3 S1= d1 b3 S1= d2 (39)
 b3 4 +P + P có độ lợi kênh trung bình cao hơn so với UE2. Mật
 b3|S1=d1 b3|S1=d2 −
 độ công suất nhiễu AWGN khởi tạo là 1,15×10 4W.
 Thông lượng giới hạn cho phép R = R = 100 Kbps.
 với các xuất lỗi được khai triển như sau: 1 2
 Giới hạn công suất cho đầu thu SIC là Ptol = 10 dBM.
 Mô phỏng sử dụng phương pháp Monte Carlo trên
 Pb |S =−d = Pb |S =d
 3 1 1 3 1 1 (40) phần mềm Matlab.
 = Pr{LLR(b3) ≥ 0|SI = −d1|H1}
 Tham số mô phỏng trình bày trong Bảng 1 để mô
 phỏng kiểm tra việc công suất tối ưu để thông lượng
 hệ thống đạt cực đại và đánh giá hiệu năng của hệ
 P | − = P |
 b3 S1= d2 b3 S1=d2 (41) thống thông qua tỷ lệ lỗi bit BER.
 = Pr{LLR(b3) < 0|SI = −d2|H1}
 Bảng 1: Tham số mô phỏng
 Tương tự cho việc khai triển LLR(b3) như (29) và giải Thông số Giá trị
 các bất phương trình trong (40) và (41):
 Tổng băng thông hệ thống, B 21 MHz
 Số khối nguồn khả dụng, ω 1
 Pb3|S1{=−d1 = Pb3|S1=d1 } { }
 d2 − d1 3d1 + d2 (42)
 = Pr N > + Pr N > Tổng công suất đường xuống, Pt 40 W
 1kI 2 1kI 2
 Ngưỡng hoạt động của đầu thu 10 dBm
 SIC, Pth
 Ngưỡng dưới của thông lượng, 100 Kbps
 Pb3|S1{=−d2 = Pb3|S1=d2 }
 d2 − d1 d1 + 3d2 (43) R1 = R2
 = Pr < N1I < .
 2 2 −4
 Mật độ công suất nhiễu N0 1,15x10 W
 −
 1,15x10 6 W
 Tương tự UE2, hàm mật độ của N1kI
 dUE1 = 100 m
 ( ( ) ) Khoảng cách từ UE1 và UE2 đến
 || || 2 UE2
 √H1k −|| ||2 √n trạm phát tương ứng là d = 200 m
 fN1kI (n) = exp H1k ,
 N0π N0
 Mức công suất phân bổ tối ưu
 b
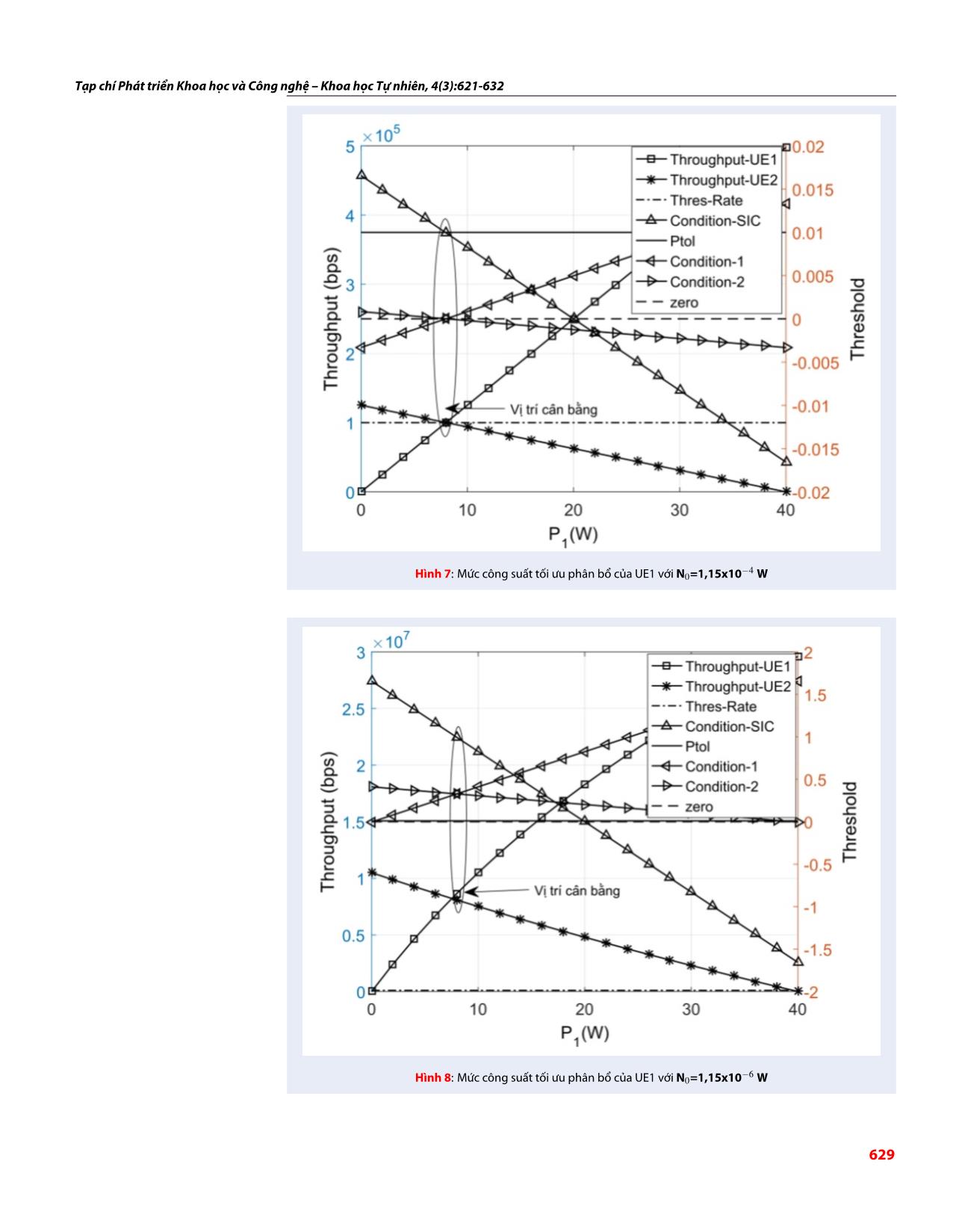
 xác suất lỗi bit 3 được xác định: Bằng việc tính toán lý thuyết thông qua (14), mức
 √
 công suất tối ưu cho hệ thống là P1 = 8 W và P2 = 32
 1 G (d − d )2 /N
 P ≈ (1 − 1 2 1 0 W. Tức là, hệ số phân bổ công suất cho UE1 và UE2
 b3 − 2
 2 √ 4 + G1 (d2 d1) /N0 là (P1,P2) = (0,2;0,8). Kiểm chứng trên mô phỏng
 1 G (3d + d )2 /N như Hình 7 bằng cách khảo sát công suất P từ 0
 − 1 1 2 0 (44) 1
 2
 2√ 4 + G1 (3d1 + d2) /N0 W đến 40 W, mức phân bổ công suất tối ưu đạt được
 2 tại P = 8 W như lý thuyết và thỏa mãn 2 điều kiện
 1 G1 (d1 + 3d2) /N0 1
 + 2 ) nghiệm trong (14) (Condition-1 và Condition-2 như
 2 4 + G1 (d1 + 3d2) /N0
 hình vẽ). Đồng thời thông lượng của UE1 bằng UE2
 và được xem như điểm cân bằng của hệ thống. Khi
 Giản đồ chòm sao Hình 4 cho thấy Pb3 = Pb4 . Xác suất
 N N = 1,15 × 10−6
 lỗi bit của UE1 là: giảm 0 đến 0 W, thông lượng tại
 √ vị trí cân bằng cho cả 2 UE tăng đến R1 = R2 = 8,07
 − 2 Mbps như Hình 8 và mức công suất phân bổ cho UE1
 ≈ 1 − G1 (d2 d1) /N0
 P_UE1 (1 2 vẫn đạt được P1 = 8 W.
 2√ 4 + G1 (d2 − d1) /N0
 1 G (3d + d )2 /N
 − 1 1 2 0 (45) Hiệu năng hệ thống NOMA đường xuống sử
 2 2
 √ 4 + G1 (3d1 + d2) /N0 dụng LLR
 1 G (d + 3d )2 /N
 + 1 1 2 0 ) Dựa trên mức công suất tối ưu đạt được ở trên với hệ
 2 4 + G (d + 3d )2 /N
 1 1 2 0 số công suất phân bổ (P1,P2) = (0,2, 0,8), hiệu năng
 628
Tạp chí Phát triển Khoa học và Công nghệ – Khoa học Tự nhiên, 4(3):621-632
 −4
 Hình 7: Mức công suất tối ưu phân bổ của UE1 với N0=1,15x10 W
 −6
 Hình 8: Mức công suất tối ưu phân bổ của UE1 với N0=1,15x10 W
 629
Tạp chí Phát triển Khoa học và Công nghệ – Khoa học Tự nhiên, 4(3):621-632
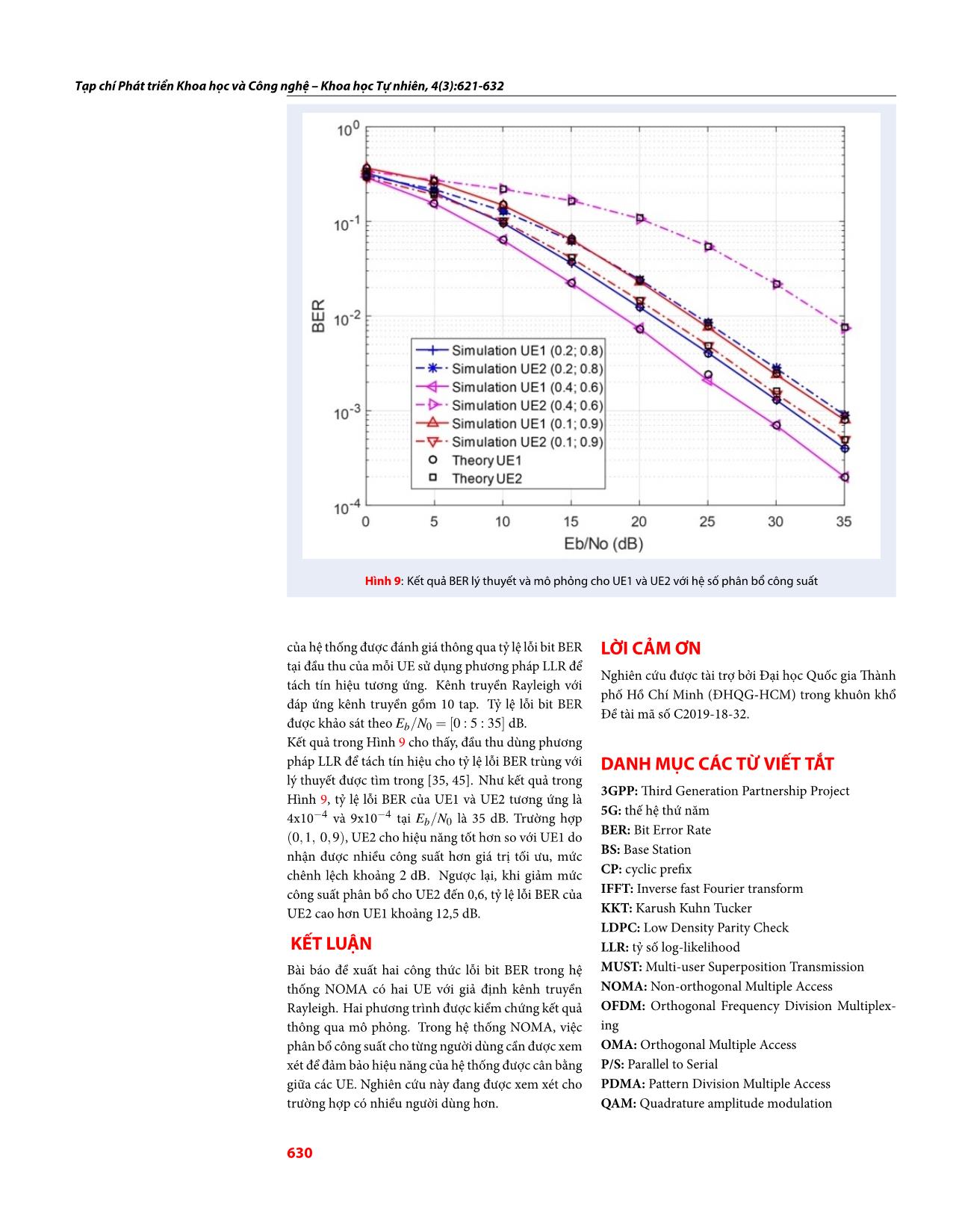
 Hình 9: Kết quả BER lý thuyết và mô phỏng cho UE1 và UE2 với hệ số phân bổ công suất
 của hệ thống được đánh giá thông qua tỷ lệ lỗi bit BER LỜI CẢM ƠN
 tại đầu thu của mỗi UE sử dụng phương pháp LLR để
 Nghiên cứu được tài trợ bởi Đại học Quốc gia Thành
 tách tín hiệu tương ứng. Kênh truyền Rayleigh với
 phố Hồ Chí Minh (ĐHQG-HCM) trong khuôn khổ
 đáp ứng kênh truyền gồm 10 tap. Tỷ lệ lỗi bit BER
 Đề tài mã số C2019-18-32.
 được khảo sát theo Eb/N0 = [0 : 5 : 35] dB.
 Kết quả trong Hình 9 cho thấy, đầu thu dùng phương
 pháp LLR để tách tín hiệu cho tỷ lệ lỗi BER trùng với DANH MỤC CÁC TỪ VIẾT TẮT
 lý thuyết được tìm trong [35, 45]. Như kết quả trong
 3GPP: Third Generation Partnership Project
 Hình 9, tỷ lệ lỗi BER của UE1 và UE2 tương ứng là
 −4 −4 5G: thế hệ thứ năm
 4x10 và 9x10 tại Eb/N0 là 35 dB. Trường hợp
 BER: Bit Error Rate
 (0,1, 0,9), UE2 cho hiệu năng tốt hơn so với UE1 do
 nhận được nhiều công suất hơn giá trị tối ưu, mức BS: Base Station
 chênh lệch khoảng 2 dB. Ngược lại, khi giảm mức CP: cyclic prefix
 công suất phân bổ cho UE2 đến 0,6, tỷ lệ lỗi BER của IFFT: Inverse fast Fourier transform
 UE2 cao hơn UE1 khoảng 12,5 dB. KKT: Karush Kuhn Tucker
 LDPC: Low Density Parity Check
 KẾT LUẬN LLR: tỷ số log-likelihood
 Bài báo đề xuất hai công thức lỗi bit BER trong hệ MUST: Multi-user Superposition Transmission
 thống NOMA có hai UE với giả định kênh truyền NOMA: Non-orthogonal Multiple Access
 Rayleigh. Hai phương trình được kiểm chứng kết quả OFDM: Orthogonal Frequency Division Multiplex-
 thông qua mô phỏng. Trong hệ thống NOMA, việc ing
 phân bổ công suất cho từng người dùng cần được xem OMA: Orthogonal Multiple Access
 xét để đảm bảo hiệu năng của hệ thống được cân bằng P/S: Parallel to Serial
 giữa các UE. Nghiên cứu này đang được xem xét cho PDMA: Pattern Division Multiple Access
 trường hợp có nhiều người dùng hơn. QAM: Quadrature amplitude modulation
 630
Tạp chí Phát triển Khoa học và Công nghệ – Khoa học Tự nhiên, 4(3):621-632
 QPSK: Quadrature phase-shift keying 6. Tran TN, Voznak M. Multi-Points Cooperative Relay in NOMA
 S/P: Serial to Parallel System with N-1 DF Relaying Nodes in HD/FD Mode for N User
 Equipments with Energy Harvesting. Electronics. 2019;8(2).
 SCMA: Sparse Code Multiple Access Available from: https://doi.org/10.3390/electronics8020167.
 SIC: Successive Interference Cancellation 7. Higuchi K, Benjebbour A. Non-orthogonal multiple access
 TCMA: Trellis Coded Multiple Access (NOMA) with successive interference cancellation for fu-
 ture radio access. IEICE Transactions on Communications.
 UE: User Equipment 2015;98(3):403–414. Available from: https://doi.org/10.1587/
 transcom.E98.B.403.
 XUNG ĐỘT LỢI ÍCH 8. Li A, Lan Y, Chen X, Jiang H. Non-orthogonal multiple access
 (NOMA) for future downlink radio access of 5G. China Com-
 Nhóm tác giả cam kết không mâu thuẫn quyền lợi và munications. 2015;12:28–37. Available from: https://doi.org/
 nghĩa vụ của các thành viên. 10.1109/CC.2015.7386168.
 9. Ali MS, Tabassum H, Hossain E. Dynamic user clustering and
 ĐÓNG GÓP CỦA TÁC GIẢ power allocation for uplink and downlink non-orthogonal
 multiple access (NOMA) systems. IEEE Access. 2016;4:6325–
 Tácgiả Ngô Thanh Hãi chịu trách nhiệm viết bản thảo, 6343. Available from: https://doi.org/10.1109/ACCESS.2016.
 thực hiện mô phỏng, và tính toán các công thức. 2604821.
 10. Cui J, Ding Z, Fan P, Al-Dhahir N. Unsupervised Machine
 Tác giả Nguyễn Thái Công Nghĩa tham gia thảo luận Learning-Based User Clustering in Millimeter-Wave-NOMA
 đề xuất phương pháp thực hiện, và phối hợp chỉnh Systems. IEEE Transactions on Wireless Communications.
 sửa bản thảo. 2018;17(11):7425–7440. Available from: https://doi.org/10.
 1109/TWC.2018.2867180.
 Tác giả Đặng Lê Khoa kiểm tra và chỉnh sửa bản thảo 11. Yan C, Harada A, Benjebbour A, Lan Y, Li A, Jiang H, editors.
 trước khi nộp. Đề xuất phương pháp, phối hợp thực Receiver Design for Downlink Non-Orthogonal Multiple Ac-
 hiện mô phỏng và tính toán các công thức, liên hệ cess (NOMA). 2015 IEEE 81st Vehicular Technology Confer-
 ence (VTC Spring). 2015;p. 11–14. Available from: https://doi.
 phản hồi các câu hỏi và yêu cầu của phản biện và ban org/10.1109/VTCSpring.2015.7146043.
 biên tập tạp chí. 12. Raju MS, Ramesh A, Chockalingam A, editors. BER analysis
 of QAM with transmit diversity in Rayleigh fading channels.
 TÀI LIỆU THAM KHẢO IEEE Global Telecommunications Conference (IGLOBECOM).
 2003;p. 1–5.
 1. Zeng M, Yadav A, Dobre OA, Tsiropoulos GI, Poor HV. On the
 13. Ding Z, Yang Z, Fan P, Poor HV. On the Performance of
 sum rate of MIMO-NOMA and MIMO-OMA systems. IEEE Wire-
 Non-Orthogonal Multiple Access in 5G Systems with Ran-
 less Communications Letters. 2017;6(4):534–537. Available
 domly Deployed Users. IEEE Signal Processing Letters.
 from: https://doi.org/10.1109/LWC.2017.2712149.
 2014;21(12):1501–1505. Available from: https://doi.org/10.
 2. Yuan L, Pan J, Yang N, Ding Z, Yuan J. Successive Interfer-
 1109/LSP.2014.2343971.
 ence Cancellation for LDPC Coded Non-Orthogonal Multi-
 14. Cho YS, Kim J, Yang WY, Kang CG. MIMO-OFDM Wireless Com-
 ple Access Systems. IEEE Transactions on Vehicular Technol-
 munications with MATLAB: Wiley. 2010;Available from: https:
 ogy. 2018;67(6):5460–5464. Available from: https://doi.org/10.
 //doi.org/10.1002/9780470825631.
 1109/TVT.2018.2831213.
 15. Goldsmith A. Wireless Communications: Cambridge Uni-
 3. Zhang S, Xu X, Lu L, Wu Y, He G, Chen Y, editors. Sparse
 versity Press. 2005;Available from: https://doi.org/10.1017/
 code multiple access: An energy efficient uplink approach for
 CBO9780511841224.
 5G wireless systems. IEEE Global Communications Confer-
 16. Viterbi AJ. An intuitive justification and a simplified
 ence. 2014;p. 8–12. Available from: https://doi.org/10.1109/
 implementation of the MAP decoder for convolu-
 GLOCOM.2014.7037563.
 tional codes. IEEE Journal on Selected Areas in Com-
 4. Ding Z, Adachi F, Poor HV. The application of MIMO to non-
 munications. 1998;16(2):260–264. Available from:
 orthogonal multiple access. IEEE Transactions on Wireless
 https://doi.org/10.1109/49.661114.
 Communications. 2016;15(1):537–552. Available from: https:
 17. Hara S, Prasad R. Multicarrier Techniques for 4G Mobile Com-
 //doi.org/10.1109/TWC.2015.2475746.
 munications: Artech House Publishers. 2003;.
 5. Americar G. Wireless Technology Evolution Towards 5G: 3GPP
 release 13 to release 15 and beyond. 2017;.
 631
Science & Technology Development Journal – Natural Sciences, 4(3):621-632
 Open Access Full Text Article Research Article
Performance of non-orthogonal multiple access downlink system
using the Log-Likelihood ratio
Ngo Thanh Hai, Nguyen Thai Cong Nghia, Dang Le Khoa
 ABSTRACT
 Non-orthogonal multiple access (NOMA) is one of the potential technologies for fifth generation
 (5G) cellular networks. This technique can combine with other techniques such as Orthogonal Fre-
 Use your smartphone to scan this quency Division Multiplexing (OFDM) and Multiple Input Multiple Output (MIMO). In NOMA down-
 QR code and download this article link, signals from multiple users are superposed in time-frequency domain. Hence, NOMA systems
 have a larger throughput than orthogonal multiple access systems. There are several schemes for
 NOMA detection. The successive interference cancellation (SIC) is commonly used to decode de-
 sired signals at the receivers. Some NOMA schemes with SIC are ideal SIC, symbol-level SIC and
 codeword-level SIC. The previous studies showed that the log-likelihood ratio (LLR) has a perfor-
 mance as ideal SIC. In this paper, we derive the bit error rate for a NOMA downlink system with 2
 users (UE) using LLR receiver. This study considers the system over a Rayleigh fading channel and
 the presence of Additive White Gaussian Noise. The closed-form equations have been proposed
 for each user with QPSK mapping. The simulation results show that the performance of the system
 is consistent with the proposed formula
 Key words: Non-orthogonal multiple access (NOMA), Performance, 5G cellular, Log-Likelihood
 ratio (LLR)
 University of Science, VNU-HCM,
 Vietnam
 Correspondence
 Dang Le Khoa, University of Science,
 VNU-HCM, Vietnam
 History
 • Received: 21-12-2018 
 • Accepted: 07-8-2020 
 • Published: 16-8-2020
 DOI : 10.32508/stdjns.v4i3.662 
 Copyright
 © VNU-HCM Press. This is an open-
 access article distributed under the
 terms of the Creative Commons
 Attribution 4.0 International license.
 Cite this article : Hai N T, Nghia N T C, Khoa D L. Performance of non-orthogonal multiple access 
 down-link system using the Log-Likelihood ratio . Sci. Tech. Dev. J. - Nat. Sci.; 4(3):621-632.
 632