Bài giảng Tin học ứng dụng - Chương 3: Ứng dụng Excel trong một số bài toán kinh tế

 bớt tổn thất do hao mòn vô hình. 
  Hạn chế: 
  Có thể gây nên sự đột biến về giá thành sản phẩm trong 
 những năm đầu do chi phí khấu hao lớn (gây bất lợi trong 
 cạnh tranh, nên các doanh nghiệp chưa ổn định, chưa có lãi 
 thì không nên áp dụng PP này). 
02/09/2015 8 
 Các loại khấu hao nhanh 
 1. Khấu hao theo tổng số năm sử dụng 
 2. Khấu hao theo số dư giảm dần 
 3. Khấu hao nhanh với tỉ lệ khấu hao tùy chọn 
02/09/2015 9 
 1. Khấu hao theo tổng số năm sử dụng 
 • Cú pháp: SYD(Cost, Salvage, Life, Period) 
 • Ý nghĩa: Tínhtổng khấu hao hàng năm của một TSCĐ trong 
 một khoản thời gian xác định. 
 • Đối số: 
 • Cost: Nguyên giácủ a TSCĐ (Chi phí ban đầu) 
 • Salvage: Giá trịthả i hồi (Thu hồi) 
 • Life: Tuổi thọ kinh tế 
 • Period: Kỳ tính khấu hao 
02/09/2015 10 
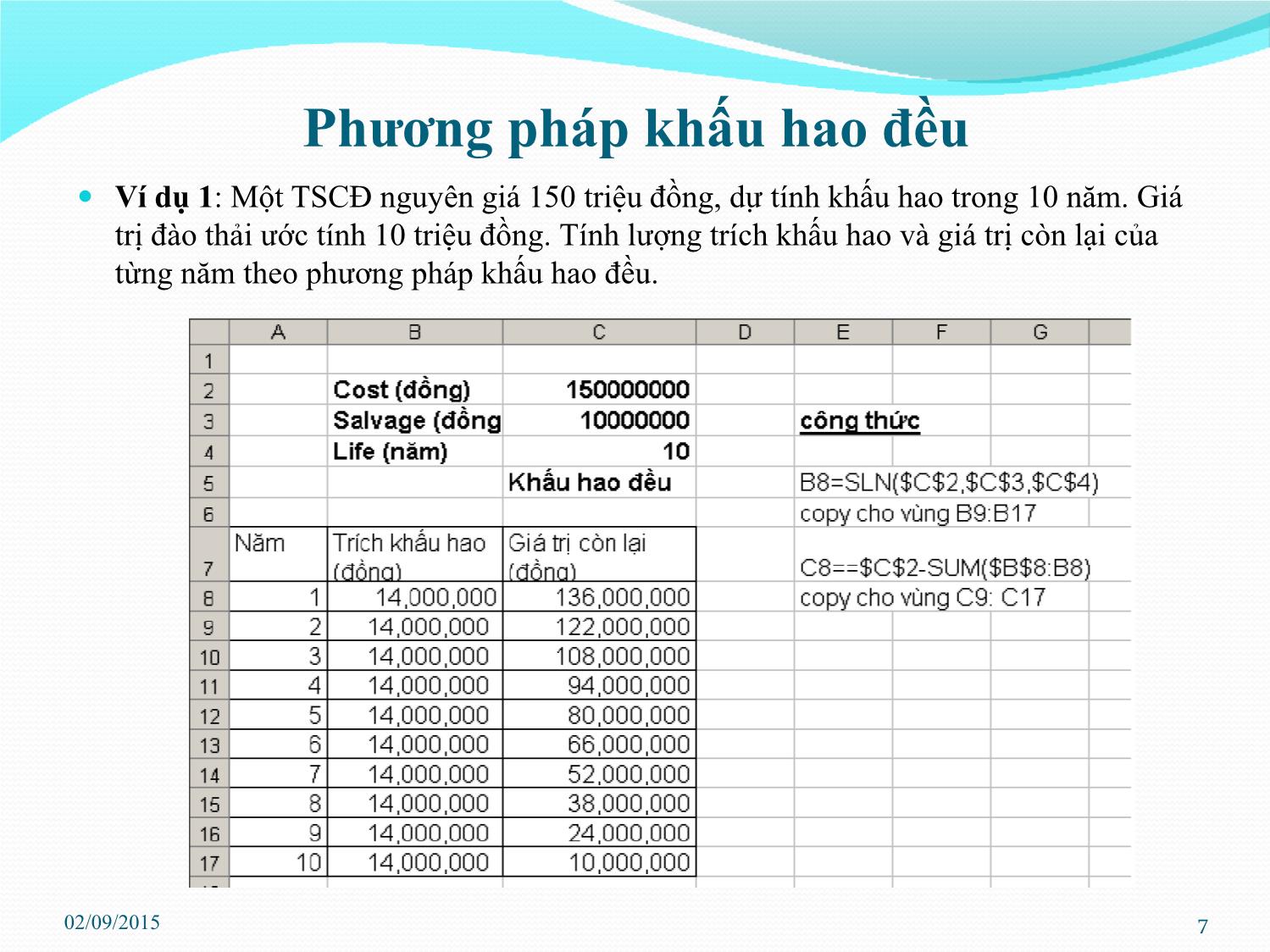
 1. Khấu hao theo tổng số năm sử dụng 
 Ví dụ2 : Với các số liệu tương ứng như ví dụ1 . Hãy tính lượng trích khấu 
 hao và giátrị cò n lại cho từng năm theo phương pháp khấu hao theo tổng số 
 năm sử dụng. 
 2. Khấu hao theo số dư giảm dần 
 Cú pháp: DB(cost, salvage, life, period, [month]) 
 Ý nghĩa: Tính khấu hao cho một tài sản sử dụng phương pháp số dư
 giảm dần theo một mức cố định trong một khoản thời gian xác định.
 Đối số 
  Cost: Nguyên giá 
  Salvage: Giá trị thải hồi 
  Life: Tuổi thọ kinh tế 
  Period: Kỳ tính khấu hao. Kỳ khấu hao phải dùng cùng đơn vị 
 với tuổi thọ. 
  Month: Số tháng trong năm đầu tiên. Nếu bỏqua đối số month, 
 nó được giả định là 12. 
 Lưu ý: Do có tính đến số tháng ở năm đầu tiên, nên nếu năm đầu tiên 
 có số tháng là m (m≠ 12) thì còn cần thêm 12-m tháng ởnăm thứ 
 T+1 mới khấu hao hết giá trị dự tính. 
02/09/2015 12 
 2. Khấu hao theo số dư giảm dần 
 Ví dụ3 : Sử dụng các số liệu như ví dụ1 . Tính lượng tríchkhấ u hao và giátrị 
 còn lại cho từng năm theo phương pháp số dư giảm dần, biết năm đầu tiên có5 
 tháng. 
 3. Khấu hao nhanh với tỉ lệ khấu hao tùy chọn 
  Cú pháp: DDB(cost, salvage, life, period, [factor]) 
  Ý nghĩa: Tínhkhấu hao cho một TSCĐ theo phương pháp tỷ lệ 
 giảm dần (số dư giảm gấp đôi hay một tỷ lệ giảm khác do yêu
 cầu quản lý có thể được lựa chọn). 
  Đối số: 
  Cost: Nguyên giá 
  Salvage: Giá trị thải hồi 
  Life: Tuổi thọ kinh tế 
  Period: Kỳ tính khấu hao. Kỳ khấu hao phải dùng cùng đơn 
 vị với tuổi thọ. 
  Factor (Tùy chọn). Tỷ lệ để giảm dần số dư. Nếu bỏ qua 
 đối số factor, nó được giả định bằng 2 (phương pháp số dư 
 giảm kép). 
02/09/2015 14 
 3. Khấu hao với tỉ lệ khấu hao tùy chọn 
 Ví dụ 4: Sử dụng các giátrị cho như ví dụ1 . Tính lượng trích khấu hao TSCĐ và 
 giátrị cò n lại cho từng năm theo phương pháp khấu hao số dư giảm dần với tỉ lệ tùy 
 chọn. 
 Bài toán: đánh giá hiệu quả vốn đầu tư
  Đánh giá hiệu quả vốn đầu tư là tiền đề quan trọng cho việc 
 quyết định lựa chọn phương án đầu tư của doanh nghiệp. 
  Các hàm đánh giá hiệu quả vốn đầu tư đơn giản, nhanh chóng 
 và chính xác trong Excel cũng sẽ là một lựa chọn khôn ngoan 
 cho các nhà quản trị tài chính của doanh nghiệp. 
  Excel cung cấp cho chúng ta một nhóm các hàm tính toán giá 
 trị dòng tiền như FV, PV, PMT,... 
02/09/2015 16 
 Tính giá trị tương lai 
 Ví dụ 1: Một người gửi 10 triệu đồng vào ngân hàng với lãi suất 
 7%/năm. Hỏi số tiền thu được sau 2 năm? 
 Hàm FV được dùng để xác định tổng số tiền mà bạn nhận được trong 
 tương lai khi đầu tư một số tiền nhất định (định kỳ) vào một dự án, 
 có lãi suất không đổi. 
 Cú pháp: FV(rate, nper, pmt, pv, type) 
  rate là lãi suất mỗi kỳ 
  nper là tổng số kỳ tính lãi 
  pmt là số tiền phải trả đều trong mỗi kỳ, nếu bỏ trống thì coi là 0 
  pv là giá trị hiện tại của khoản đầu tư, nếu bỏ trống thì coi là 0 
  type là hình thức thanh toán. Nếu type = 1 thì thanh toán đầu kỳ, 
 nếu type = 0 thì thanh toán vào cuối mỗi kỳ (mặc định) 
02/09/2015 17 
 Tính giá trị tương lai 
  Ví dụ 2: Một người gửi 10 triệu đồng vào ngân hàng với lãi 
 suất 7%/năm và hàng năm gửi thêm 2 triệu đồng. Hỏi số tiền 
 thu được sau 2 năm? 
 Chú ý: các tham số mang dấu dương nếu đó là số tiền thu về, 
 mang dấu âm nếu đó là số tiền phải bỏ ra. 
02/09/2015 18 
 Tính giá trị hiện tại 
  Ví dụ 1: Một người muốn có số tiền tiết kiệm 100 triệu sau 10 
 năm. Hỏi bây giờ người đó phải gửi vào ngân hàng bao nhiêu? 
 Biết rằng lãi suất ngân hàng là 7%/năm. 
  Cú pháp: PV(rate, nper, pmt, fv, type) 
  rate là lãi suất mỗi kỳ 
  nper là tổng số kỳ tính lãi 
  pmt là số tiền phải trả đều trong mỗi kỳ, nếu bỏ trống thì coi 
 là 0 
  fv là giá trị tương lai của khoản đầu tư 
  type là hình thức thanh toán. Nếu type = 1 thì thanh toán 
 đầu kỳ, nếu type = 0 thì thanh toán vào cuối mỗi kỳ (mặc 
 định) 
02/09/2015 19 
 Tính giá trị hiện tại 
  Ví dụ 2: Để nhận được một khoản tiền 1000$ sau 5 năm nữa 
 ngay bây giờ cần phải gửi vào ngân hàng một khoản tiền là bao 
 nhiêu biết lãi suất ngân hàng là 4.5%/ năm. 
  Ví dụ 3: Bạn muốn có 100 triệu đồng trong tài khoản tiết kiệm 
 vào ngày 1/1/2015 thì vào ngày 1/1/2010 bạn phải gửi vào tài 
 khoản tiết kiệm một khoản tiền bằng bao nhiêu? Biết lãi suất 
 ngân hàng trả cố định là 10%/năm và hàng năm bạn gửi thêm 
 vào 12 triệu. 
02/09/ 2015 20 
 Tính giá trị thanh toán đều đặn theo định kỳ 
 Ví dụ: Bạn vay ngân hàng 50 triệu đồng đồng trả góp vào cuối 
 mỗi tháng, trong vòng 48 tháng. Hỏi số tiền mỗi tháng bạn phải 
 trả cho ngân hàng là bao nhiêu? Biết lãi suất ngân hàng cố định là 
 1,2%/tháng. 
 Cú pháp: PMT(rate, nper, pv, fv, type) 
  rate là lãi suất mỗi kỳ 
  nper là tổng số kỳ tính lãi 
  pv là giá trị hiện tại của khoản đầu tư, nếu bỏ trống thì coi là 0 
  fv là giá trị tương lai của khoản đầu tư 
  type là hình thức thanh toán. Nếu type = 1 thì thanh toán đầu 
 kỳ, nếu type = 0 thì thanh toán vào cuối mỗi kỳ (mặc định) 
02/09/2015 21 
 Tính giá trị thanh toán đều đặn theo định kỳ 
02/09/2015 22 
 Tính tiền lãi phải trả theo kỳ
  Ví dụ: Nếu vay ngân hàng một khoản tiền 10 triệu với lãi suất 
 12%/năm trong vòng 5 năm, trả lãi định kỳ theo năm thì lượng 
 tiền phải trả lãi cuối năm thứ nhất là bao nhiêu? 
  Cú pháp:IPMT(rate, per, nper, pv, [fv], [type]) 
  Per: Số thứ tự của kỳ cần tính lãi. 
  Các tham số khác giống các hàm đã học
02/09/2015 23 
 Tính lãi suất 
  Ví dụ: Một khoản vay 8000$ ban đầu được đề xuất thanh toán 
 200$/ tháng liên tục trong 4 năm (48 tháng). Hỏi lãi suất của 
 khoản vay này là bao nhiêu? 
  Cú pháp: RATE (nper, pmt, pv, [fv],[type],[guess]) 
  Trong đó: 
  Guess: là giá trị dự đoán. Nếu bỏ qua giá trị này, Excel sẽ tự 
 động gán cho giá trị guess = 10% 
  Các tham số khác tương tự các hàm khác 
02/09/2015 24 
 Tính lãi suất 
02/09/2015 25 
 Tính số kìthanh toán 
  Ví dụ: Bạn gửi một số tiền 1.000$ vào ngân hàng, lãi suất của 
 ngân hàng là 12%/năm, mỗi tháng bạn gửi thêm 100$. Hỏi sau 
 bao lâu bạn thu được số tiền 10.000$. Sử dụng phương pháp 
 gửi thêm tiền vào đầu kỳ. 
  Cú pháp: NPER(rate, pmt, pv, [fv], [type]) 
02/09/2015 26 
 Tính lãi suất thực tế hàng năm 
  Ví dụ: Một khoản vay ngân hàng với lãi suất danh nghĩa là 
 5,25%/ năm nhưng được tính trả lãi theo quí. Hỏi lãi suất thực 
 tế của khoản vay là bao nhiêu %/năm. 
  Cú pháp: EFFECT (nominal_rate, npery) 
  Trong đó: 
  Nominal_rate: lãi suất danh nghĩa 
  Npery: số kì tính lãi trong năm 
02/09/2015 27 
 Tính giá trịtương lai khi lãi suất thay đổi 
  Ví dụ: Một khoản tiền vay ban đầu là1000 $, vay trong 3 năm 
 với lãi suất lần lượt là3.5 %/ năm, 4%/ năm và 5%/ năm. Hỏi 
 sau thời gian trên cần thanh toán cả lãi và gốc số tiền bằng bao 
 nhiêu? 
  Cú pháp: FVSCHEDULE (principal, schedule) 
  Trong đó: 
  Principal: giátrị hiệ n tại 
  Schedule: các lãi suất từng kì 
  Công thức: =FVSCHEDULE(1000, {0.035, 0.04, 0.05}) 
02/09/2015 28 
 Tính giá trị thuần của dự án 
  Dòng tiền thuần là số tiền chêch lệch của toàn bộ các khoản thu 
 vào và chi ra trong suốt vòng đời dự án. 
  NPV là giá trị hiện tại thuần của một khoản đầu tư. Đó chính là 
 giá trị tại thời điểm hiện tại của toàn bộ dòng tiền thuần của 
 một dự án. 
  Nếu NPV > 0 thì dự án có tính khả thi 
  Nếu NPV < 0 thì dự án không mang tính khả thi (loại bỏ) 
  Nếu NPV = 0 thì tùy thuộc tình hình cụ thể và sự cần thiết 
 của dự án mà nhà đầu tư có thể quyết định loại bỏ hay chấp 
 nhận dự án. 
02/09/2015 29 
 Tính giá trị thuần của dự án 
  Cú pháp: NPV(rate, value-1, value-2, , value-n) 
  Trong đó: 
  Rate: tỉ suất chiết khấu 
  Value-1, value-2,  value-n: các khoản tiền xuất hiện tại 
 các thời điểm 1, 2, , n của kỳ phân tích với các thời điểm 
 bằng nhau 
02/09/2015 30 
 Tính giá trị thuần của dự án 
  Ví dụ: 
02/09/2015 31 
 Bài toán đầu tư chứng khoán 
  Tính lãi gộp cho một trái phiếu trả vào ngày tới hạn 
  Tính lãi gộp của một chứng khoán trả theo định kì 
  Tính tỉ suất chiết khấu của một chứng khoán 
  Tính lãi suất của một chứng khoán được đầu tư hết 
  Tính số tiền thu được vào ngày tới hạn của một chứng khoán 
 được đầu tư hết 
02/09/2015 32 
 Tính lãi gộp cho một trái phiếu trả vào ngày tới hạn 
  Ta có công thức tính như sau: 
  Trong đó: 
  ACC: lãi gộp của trái phiếu 
  Par: Mệnh giácủ a trái phiếu 
  Rate: Lãi suất hàng năm của trái phiếu 
  A: Số ngày tích lũy của trái phiếu 
  D: Số ngày của năm cơ sở 
02/09/2015 33 
 Tính lãi gộp cho một trái phiếu trả vào ngày tới hạn
  Cú pháp: ACCRINTM (issue, Settlement, rate, par, basis) 
  Trong đó: 
  Issue: ngày phát hành 
  Settlement: ngày tới hạn 
  Rate: tỷ suất của tráiphiế u 
  Par: giátrị mỗ i cuốn phiếu. Nếu bỏ qua, giátrị ngầ m định sẽ là1000 $ 
  Basis: kiểu ngày đếm cơ sở 
  Bảng liệt kê một số kiểu ngày đếm cơ sở: 
02/09/2015 34 
 Tính lãi gộp cho một trái phiếu trả vào ngày tới hạn
  Ví dụ: 
 Tính lãi gộp cho một trái phiếu kho bạc mệnh giá 500$, phát 
 hành ngày 15/5/2006 có hạn thanh toán vào ngày 25/10/2009 
 với lãi suất 4%/năm. Sử dụng mã cơ sở 1. 
  Ta có công thức tính như sau: 
 =Accrintm(date(2006,5,15),date(2009,10,25),4%,500,1) 
  Kết quả: 68.94 
02/09/2015 35 
 Tính lãi gộp của một chứng khoán trả theo định kì 
  Cú pháp: Accrint(issue, first_interest, settlement, rate, par, 
 frequency, basis) 
  Trong đó: 
  Issue: ngày phát hành chứng khoán 
  First_interest: ngày trảlã i suất đầu kì 
  Settlement: ngày thanh toán chứng khoán 
  Rate: tỉ suất (lãi suất) hàng năm của cuốn phiếu 
  Par: mệnh giácủ a cổ phiếu. Nếu bỏ quatham số này thì 
 Excel tự động gán giátrị cho nó là1000 $ 
  Frequency: làsô ́ lần trảcủ a trái phiếu trong 1 năm. Nếu 
 bằng 1: thanh toán theo hàng năm, bằng 2: thanh toán theo 
 nửa năm, nếu bằng 4: thanh toán theo quí 
  Basis: kiểu ngày đếm cơ sởđượ c sử dụng 
02/09/2015 36 
 Tính lãi gộp của một chứng khoán trả theo định kì 
  Ví dụ: Một trái phiếu kho bạc có ngày phát hành 10/3/2003, 
 ngày trả lãi kỳ đầu là 1/8/2003, ngày thanh toán trái phiếu là 
 31-5-2008. Lãi suất của trái phiếu là 10%, mệnh giá là 1000 
 USD. Dùng cơ sở 30/360 tính lãi suất gộp cho trái phiếu, thanh 
 toán theo nửa năm. 
  Công thức: 
  =ACCRINT(date(2003,3,10),date(2003,8,1),date(2008,5,31),1
 0%,1000,2,0) = 522.5($) 
02/09/2015 37 
 Tính tỉ suất chiết khấu của một chứng khoán 
  Cú pháp: DISC(settlement, maturity, Pr, redemtion, [basis]) 
  Trong đó: 
  Settlement: ngày thanh toán chứng khoán 
  Maturity: ngày tới hạn của chứng khoán 
  Pr: Giátrị củ a mỗi 100$ mệnh giácủ a chứng khoán 
  Redemtion: Giátrị phả i trảcho mỗi mệnh giá100 $ 
  Basis: kiểu ngày đếm cơ sởđượ c sử dụng 
02/09/2015 38 
 Tính tỉ suất chiết khấu của một chứng khoán 
  Ví dụ: Một trái phiếu chiết khấu giá trị 100$ có hạn thanh toán 
 ngày 15/7/2009 được mua lại vào ngày 23/3/2008 với giá 
 96.5$. Tính tỉ suất chiết khấu của trái phiếu đó sử dụng cơ sở 1. 
  =DISC(date(2008,3,23),date(2009,7,15),96.5, 100,1) =0.027 
02/09/2015 39 
 Tính lãi suất của một chứng khoán được đầu tư hết 
 Cú pháp: INTRATE(settlement, maturity, investment, 
 redemption, basis) 
 Trong đó: 
  Settlement: ngày thanh toán chứng khoán (làngà y sau ngày 
 phát hành khi chứng khoán được bán cho người mua) 
  Maturity: ngày tới hạn của chứng khoán 
  Basis: kiểu ngày đếm cơ sởđượ c sử dụng 
  Redemtion: số tiền phải trảkhi đến ngày tới hạn 
  Investment: khoản tiền đã đầu tư vào chứng khoán 
02/09/2015 40 
 Tính lãi suất của một chứng khoán được đầu tư hết 
  Ví dụ: Tính lãi suất cho một chứng khoán có ngày thanh toán 
 (ngày mua chứng khoán) là 1/2/2008, ngày tới hạn là 
 15/6/2010, tiền đầu tư là 5000$, tiền thu được là 6500$, cơ sở 1 
  =INTRATE(date(2008,1,2), date(2010, 6,15), 5000,6500,1) = 
 0.1267 
02/09/2015 41 
 Tính số tiền thu được vào ngày tới hạn của một chứng khoán 
 được đầu tư hết 
 Cú pháp: Received(settlement, maturity, investment, discount, 
 basis) 
 Trong đó: 
  Discount: tỉ suất chiết khấu 
  Settlement: ngày thanh toán chứng khoán (làngà y sau ngày phát 
 hành khi chứng khoán được bán chongườ i mua) 
  Maturity: ngày tới hạn của chứng khoán 
  Basis: kiểu ngày đếm cơ sởđượ c sử dụng 
  Investment: khoản tiền đã đầu tư vào chứng khoán 
 02/09/2015 42 
Tính số tiền thu được vào ngày tới hạn của một chứng 
 khoán được đầu tư hết 
 Ví dụ: Tính số tiền thu được vào ngày tới hạn của một trái phiếu 
 kho bạc được đầu tư hết có ngày thanh toán là 18/5/2007, ngày tới 
 hạn là 18/10/2008, tiền đầu tư là 500$, tỉ suất chiết khấu là 5.85%, 
 cơ sở 1 
 Ta có công thức tính như sau: 
 =Received(date(2007,5,18),date(2008, 10,18),500, 5.85%, 1) 
 Kết quả: =545.3$ 
02/09/2015 43