Bài giảng Nguyên lý chi tiết máy - Chương 3: Hệ bánh răng - Nguyễn Minh Kỳ
I. Phân loại
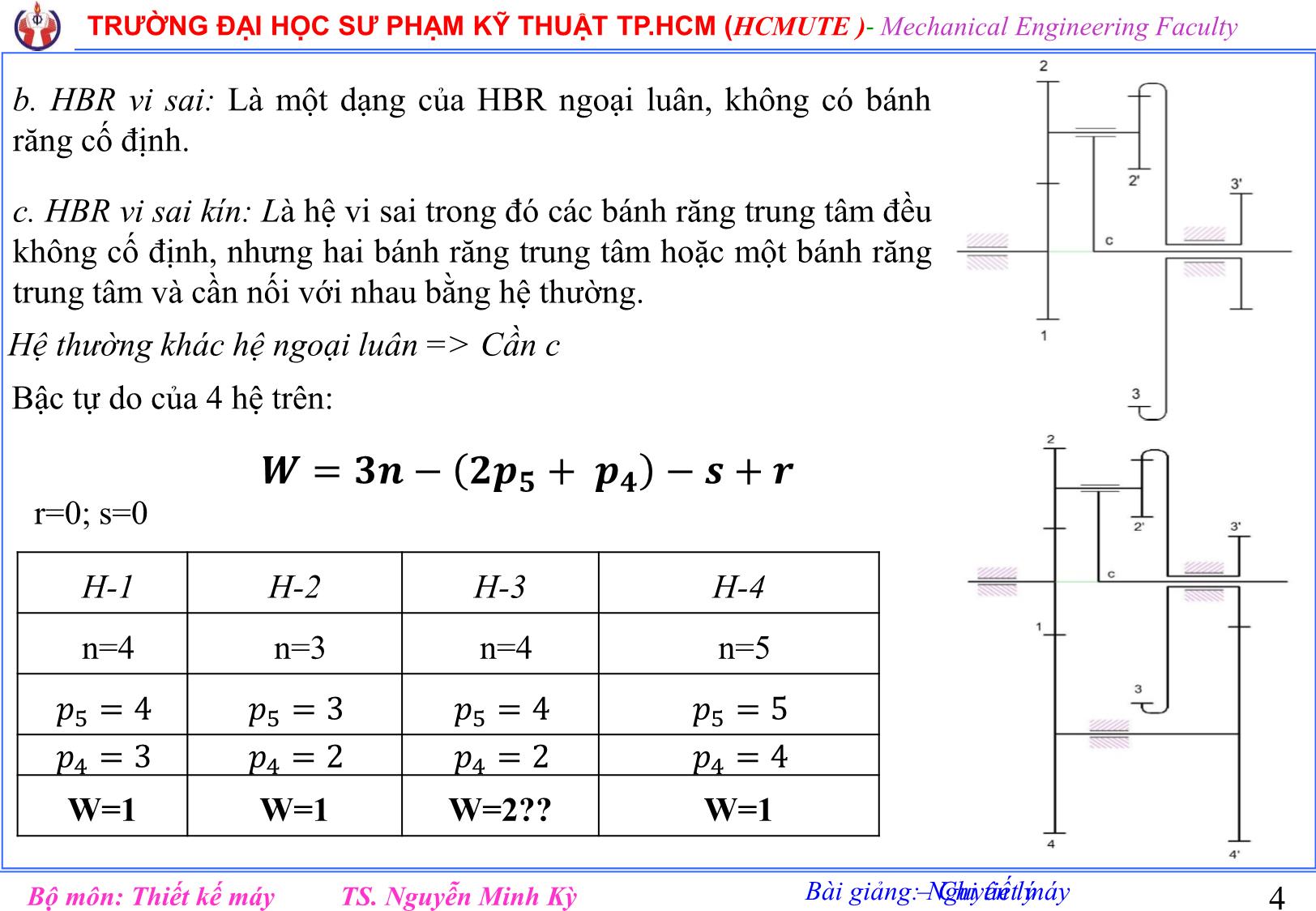
1. Hệ bánh răng thường: Hệ bánh răng thường là hệ
bánh răng trong đó tất cả các trục đều có đường tâm
trục không thây đổi.
HBR ăn khớp ngoài Ăn khớp trong
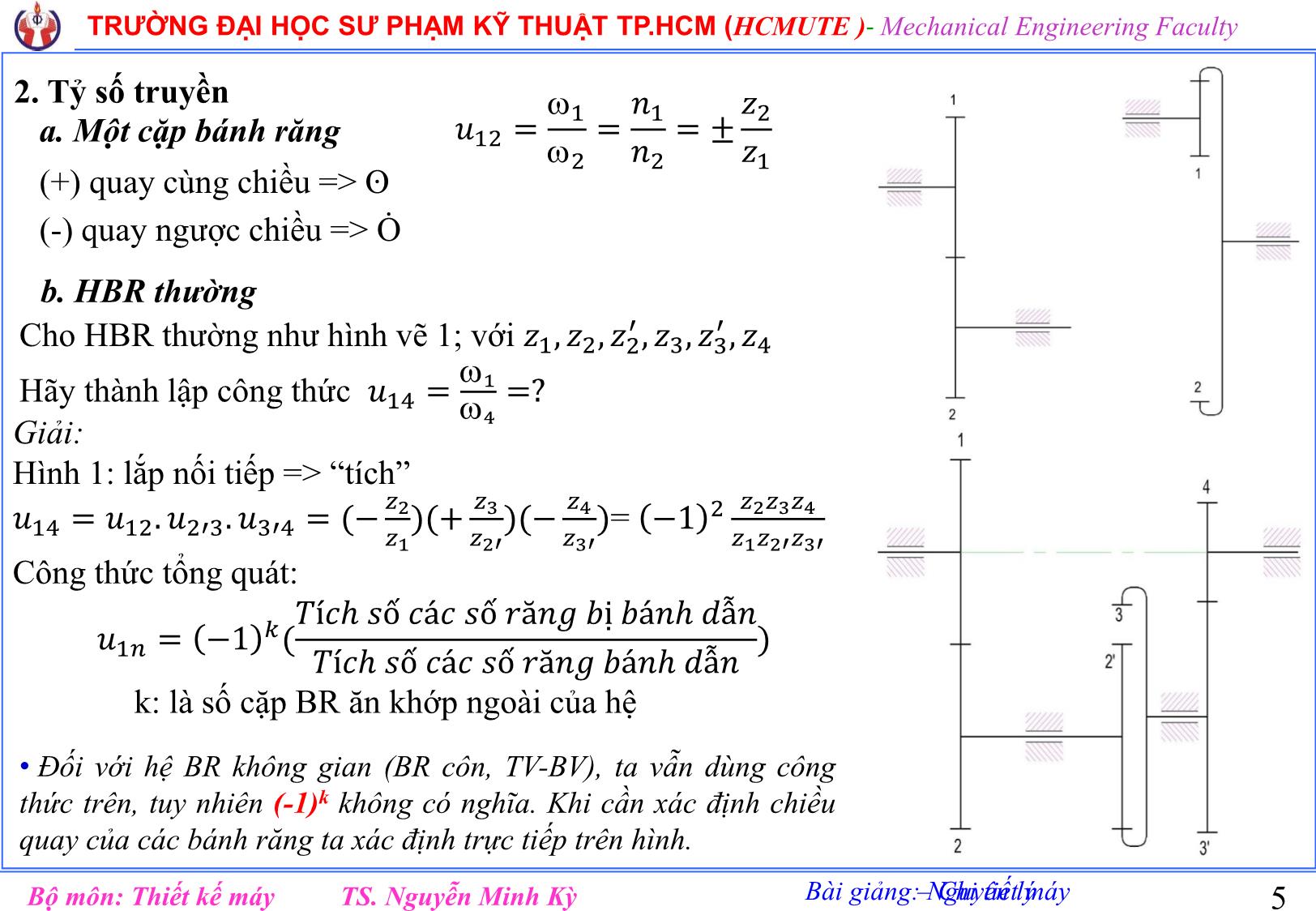
2. Hệ bánh răng ngoại luân: Là HBR có ít nhất một
BR có đường tâm thây đổi và chia làm 3 loại.
a. Hệ bánh răng hành tinh
2&2’: Bánh răng vệ tinh (hệ hành tinh)
1&3: Các bánh răng trung tâm
c: cần
Là một dạng của HBR ngoại luân, có 1 bánh trung tâm cố định.

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
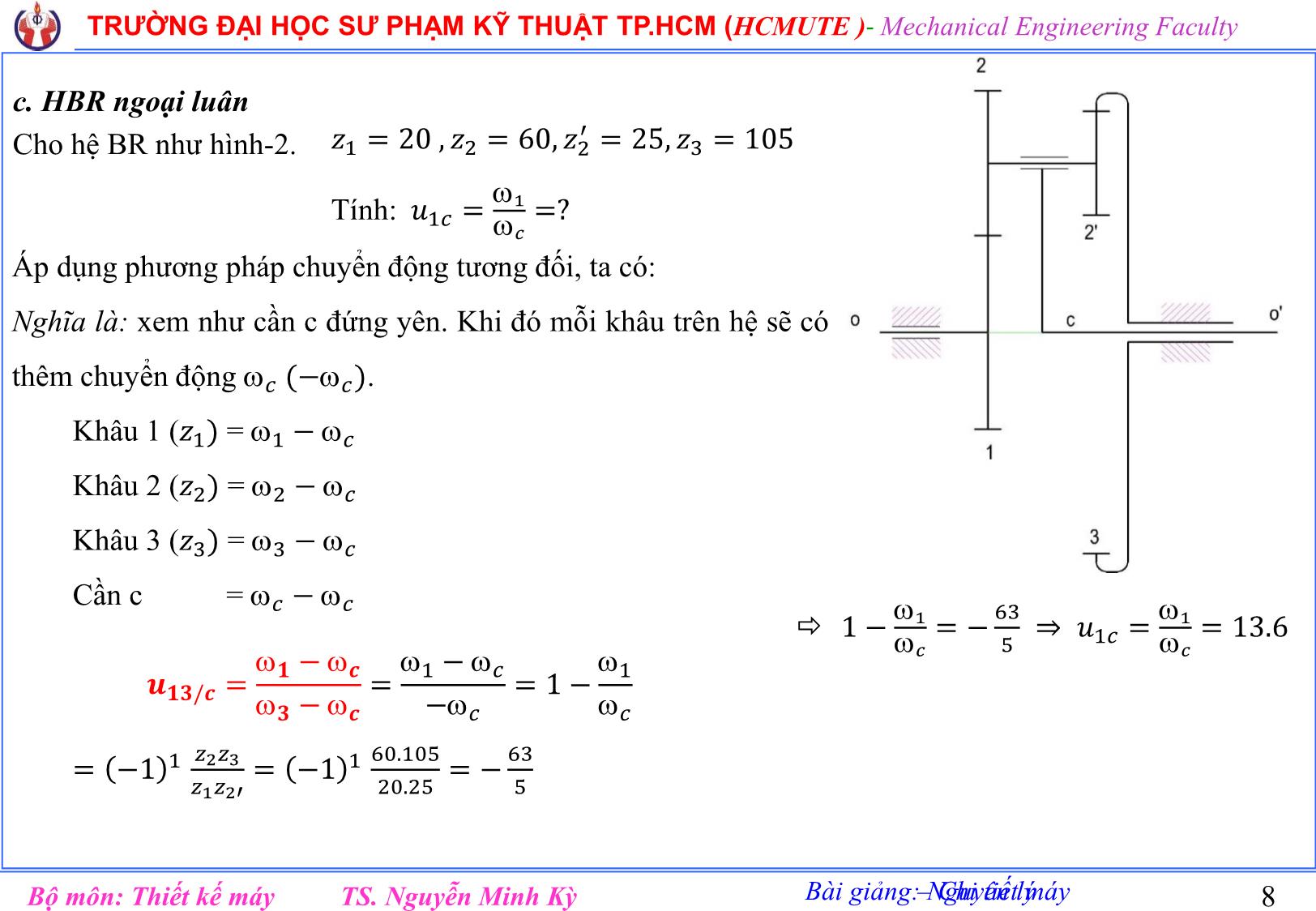
Trang 8
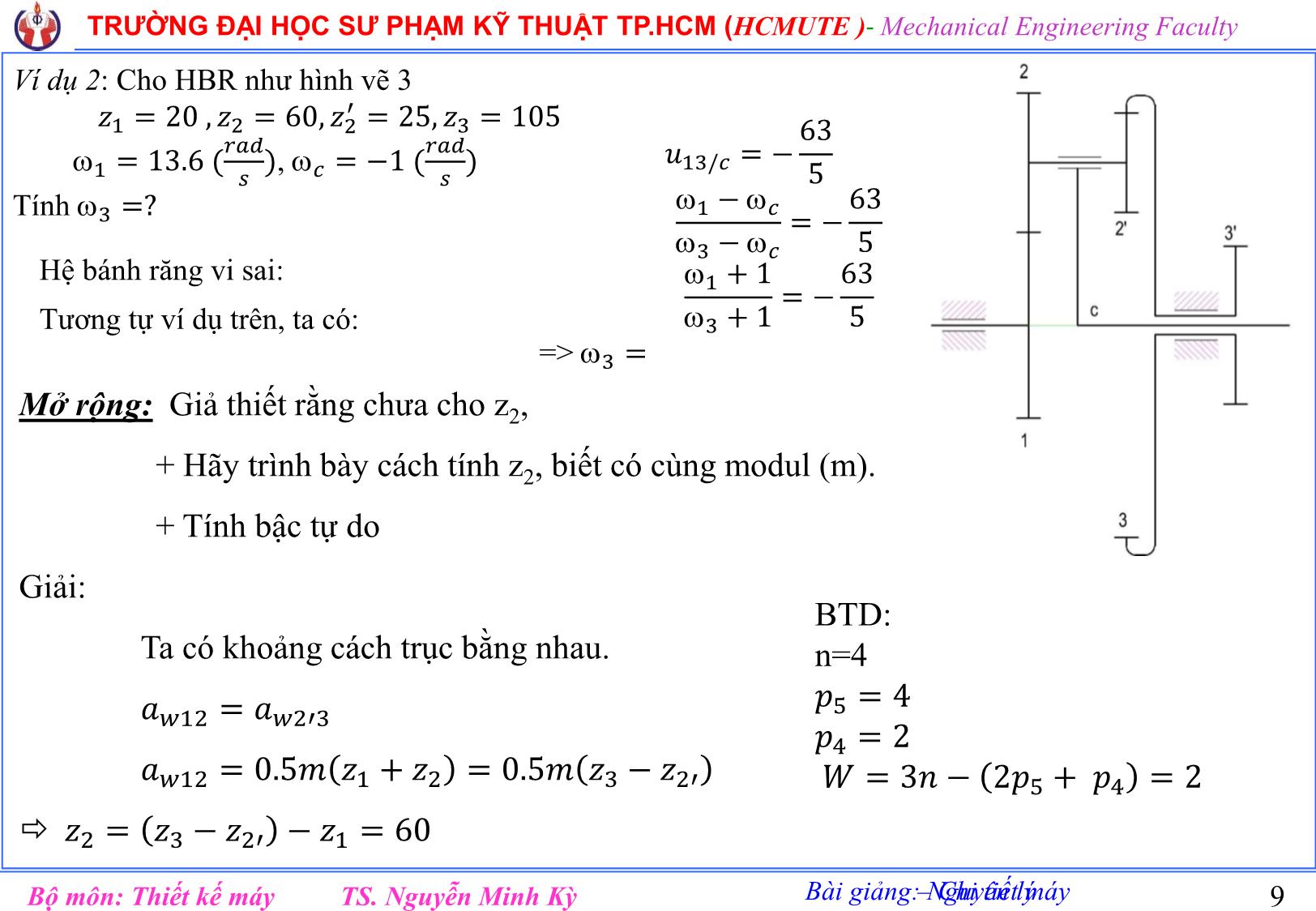
Trang 9
Bạn đang xem tài liệu "Bài giảng Nguyên lý chi tiết máy - Chương 3: Hệ bánh răng - Nguyễn Minh Kỳ", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nguyên lý chi tiết máy - Chương 3: Hệ bánh răng - Nguyễn Minh Kỳ

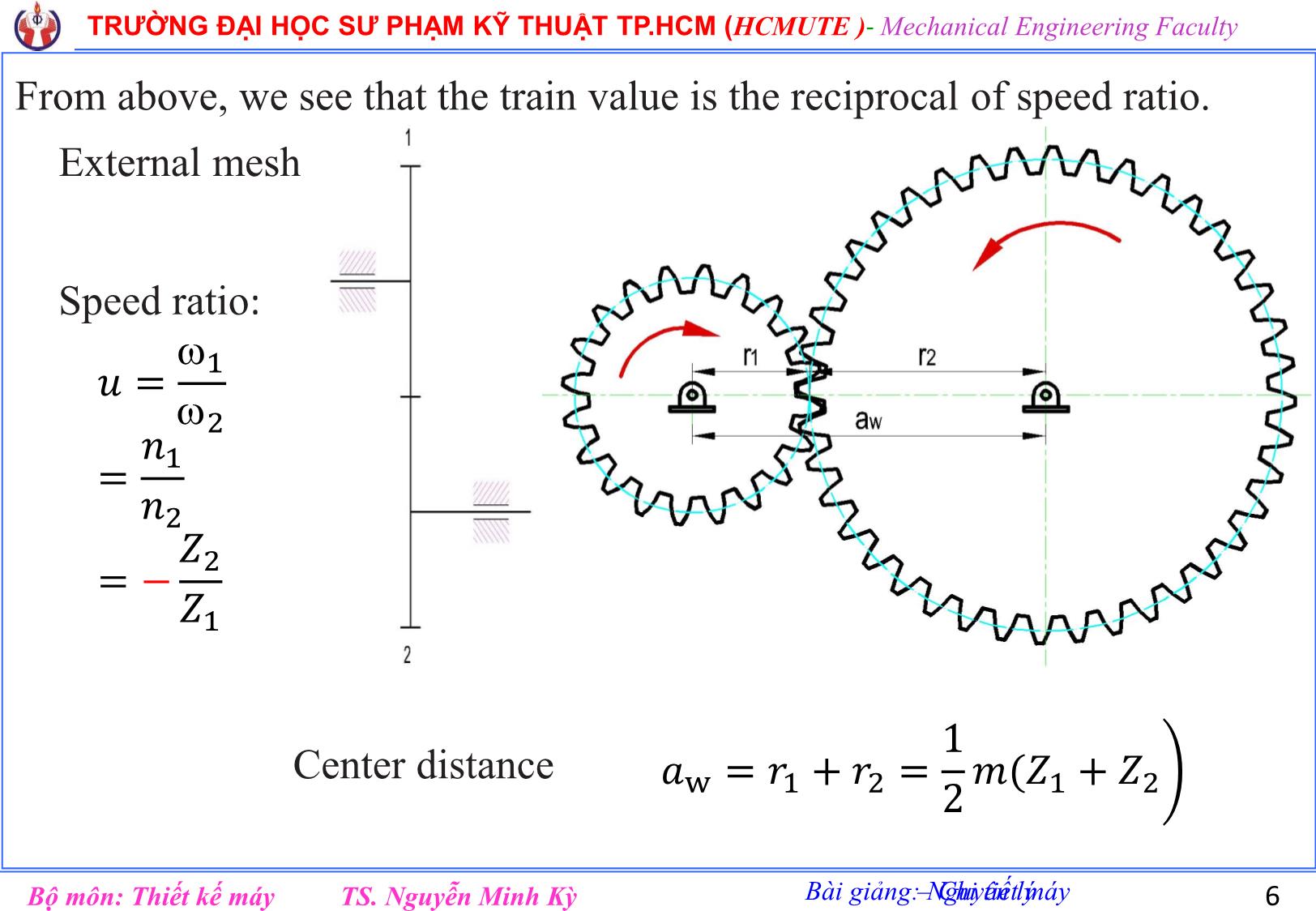
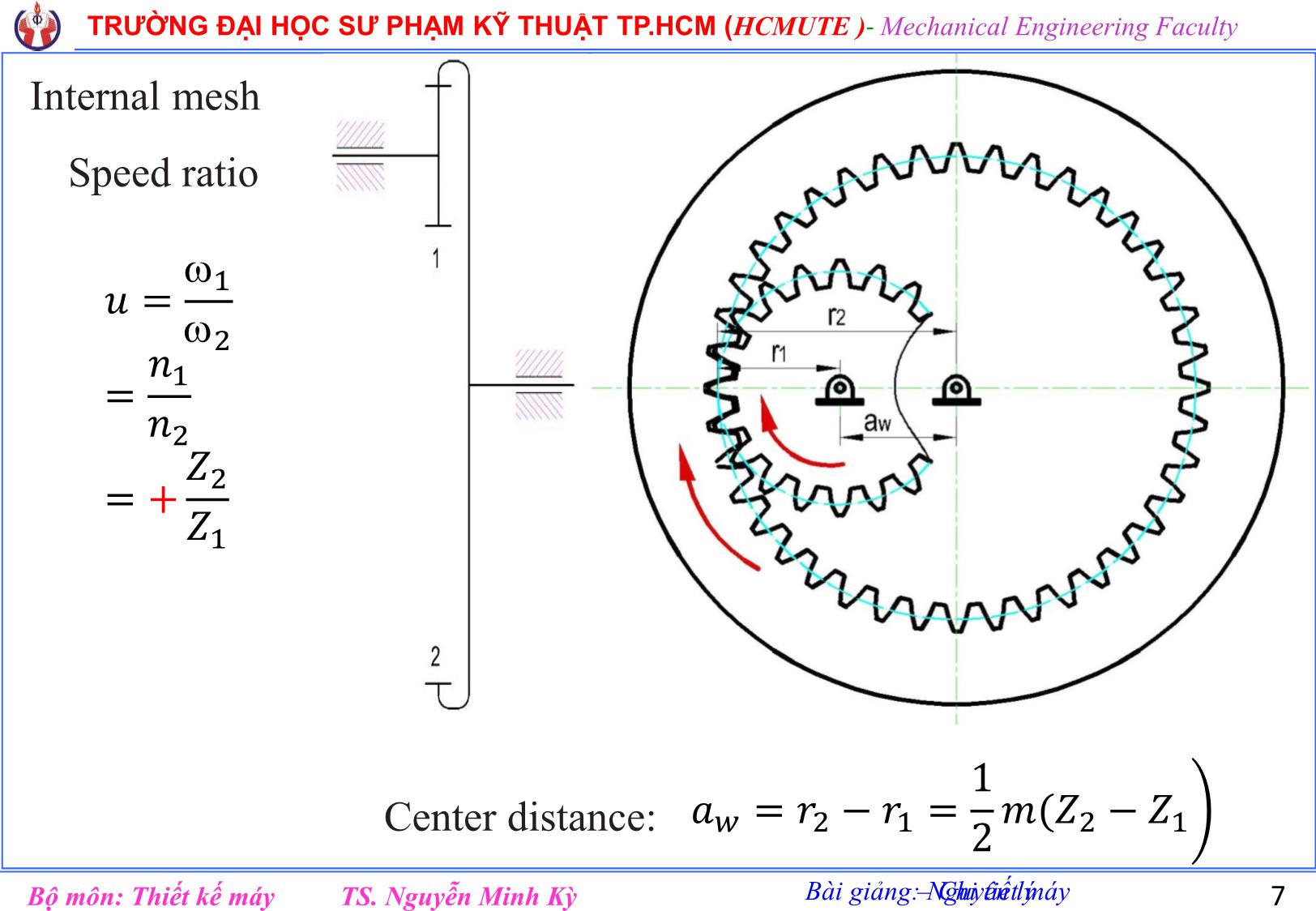
Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM HO CHI MINH CITY UNIVERSITY OF TECHNICAL AND EDUCATION KHOA CƠ KHÍ CHẾ TẠO MÁY Bộ môn: Thiết kế máy Bài giảng Phần II (Lưu hành nội bộ) Chương 3 HỆ BÁNH RĂNG Biên soạn: TS. Nguyễn Minh Kỳ 1 Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 2 HỆ BÁNH RĂNG Ta không chỉ sử dụng một cặp bánh răng mà sử dụng nhiều cặp bánh răng nối với nhau, tạo thành một hệ thống và được gọi là hệ thống bánh răng hay hệ bánh răng. Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 3 I. Phân loại 1. Hệ bánh răng thường: Hệ bánh răng thường là hệ bánh răng trong đó tất cả các trục đều có đường tâm trục không thây đổi. HBR ăn khớp ngoài Ăn khớp trong 2. Hệ bánh răng ngoại luân: Là HBR có ít nhất một BR có đường tâm thây đổi và chia làm 3 loại. a. Hệ bánh răng hành tinh 2&2’: Bánh răng vệ tinh (hệ hành tinh) 1&3: Các bánh răng trung tâm c: cần Là một dạng của HBR ngoại luân, có 1 bánh trung tâm cố định. Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 4 b. HBR vi sai: Là một dạng của HBR ngoại luân, không có bánh răng cố định. c. HBR vi sai kín: Là hệ vi sai trong đó các bánh răng trung tâm đều không cố định, nhưng hai bánh răng trung tâm hoặc một bánh răng trung tâm và cần nối với nhau bằng hệ thường. Hệ thường khác hệ ngoại luân => Cần c Bậc tự do của 4 hệ trên: 𝑾 = 𝟑𝒏 − 𝟐𝒑𝟓 + 𝒑𝟒 − 𝒔 + 𝒓 r=0; s=0 H-1 H-2 H-3 H-4 n=4 n=3 n=4 n=5 𝑝5 = 4 𝑝5 = 3 𝑝5 = 4 𝑝5 = 5 𝑝4 = 3 𝑝4 = 2 𝑝4 = 2 𝑝4 = 4 W=1 W=1 W=2?? W=1 Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 5 2. Tỷ số truyền a. Một cặp bánh răng 𝑢12 = 1 2 = 𝑛1 𝑛2 = ± 𝑧2 𝑧1 (+) quay cùng chiều => ʘ (-) quay ngược chiều => Ȯ b. HBR thường Cho HBR thường như hình vẽ 1; với 𝑧1, 𝑧2, 𝑧2 ′ , 𝑧3, 𝑧3 ′ , 𝑧4 Hãy thành lập công thức 𝑢14 = 1 4 =? Giải: Hình 1: lắp nối tiếp => “tích” 𝑢14 = 𝑢12. 𝑢2′3. 𝑢3′4 = (− 𝑧2 𝑧1 )(+ 𝑧3 𝑧2′ )(− 𝑧4 𝑧3′ )= −1 2 𝑧2𝑧3𝑧4 𝑧1𝑧2′𝑧3′ Công thức tổng quát: 𝑢1𝑛 = −1 𝑘( 𝑇í𝑐ℎ 𝑠ố 𝑐á𝑐 𝑠ố 𝑟ă𝑛𝑔 𝑏ị 𝑏á𝑛ℎ 𝑑ẫ𝑛 𝑇í𝑐ℎ 𝑠ố 𝑐á𝑐 𝑠ố 𝑟ă𝑛𝑔 𝑏á𝑛ℎ 𝑑ẫ𝑛 ) k: là số cặp BR ăn khớp ngoài của hệ • Đối với hệ BR không gian (BR côn, TV-BV), ta vẫn dùng công thức trên, tuy nhiên (-1)k không có nghĩa. Khi cần xác định chiều quay của các bánh răng ta xác định trực tiếp trên hình. Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 6 From above, we see that the train value is the reciprocal of speed ratio. External mesh Speed ratio: 𝑢 = 1 2 = 𝑛1 𝑛2 = − 𝑍2 𝑍1 Center distance 𝑎w = 𝑟1 + 𝑟2 = 1 2 𝑚(𝑍1 + 𝑍2 Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 7 Internal mesh Speed ratio 𝑢 = 1 2 = 𝑛1 𝑛2 = + 𝑍2 𝑍1 Center distance: 𝑎𝑤 = 𝑟2 − 𝑟1 = 1 2 𝑚(𝑍2 − 𝑍1 Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 8 c. HBR ngoại luân Cho hệ BR như hình-2. 𝑧1 = 20 , 𝑧2 = 60, 𝑧2 ′ = 25, 𝑧3 = 105 Tính: 𝑢1𝑐 = 1 𝑐 =? Áp dụng phương pháp chuyển động tương đối, ta có: Nghĩa là: xem như cần c đứng yên. Khi đó mỗi khâu trên hệ sẽ có thêm chuyển động 𝑐 (−𝑐). Khâu 1 (𝑧1) = 1 − 𝑐 Khâu 2 (𝑧2) = 2 − 𝑐 Khâu 3 (𝑧3) = 3 − 𝑐 Cần c = 𝑐 − 𝑐 𝒖𝟏𝟑/𝒄 = 𝟏 − 𝒄 𝟑 − 𝒄 = 1 − 𝑐 −𝑐 = 1 − 1 𝑐 = −1 1 𝑧2𝑧3 𝑧1𝑧2′ = −1 1 60.105 20.25 = − 63 5 1 − 1 𝑐 = − 63 5 ⇒ 𝑢1𝑐 = 1 𝑐 = 13.6 Bài giảng: Nguyên lý – Chi tiết máy TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM (HCMUTE )- Mechanical Engineering Faculty TS. Nguyễn Minh KỳBộ môn: Thiết kế máy 9 Ví dụ 2: Cho HBR như hình vẽ 3 𝑧1 = 20 , 𝑧2 = 60, 𝑧2 ′ = 25, 𝑧3 = 105 1 = 13.6 ( 𝑟𝑎𝑑 𝑠 ), 𝑐 = −1 ( 𝑟𝑎𝑑 𝑠 ) Tính 3 =? Hệ bánh răng vi sai: Tương tự ví dụ trên, ta có: 𝑢13/𝑐 = − 63 5 1 − 𝑐 3 − 𝑐 = − 63 5 1 + 1 3 + 1 = − 63 5 => 3 = Mở rộng: Giả thiết rằng chưa cho z2, + Hãy trình bày cách tính z2, biết có cùng modul (m). + Tính bậc tự do Giải: Ta có khoảng cách trục bằng nhau. 𝑎𝑤12 = 𝑎𝑤2′3 𝑎𝑤12 = 0.5𝑚 𝑧1 + 𝑧2 = 0.5𝑚 𝑧3 − 𝑧2′ 𝑧2 = 𝑧3 − 𝑧2′ − 𝑧1 = 60 BTD: n=4 𝑝5 = 4 𝑝4 = 2 𝑊 = 3𝑛 − 2𝑝5 + 𝑝4 = 2
File đính kèm:
 bai_giang_nguyen_ly_chi_tiet_may_chuong_3_he_banh_rang_nguye.pdf
bai_giang_nguyen_ly_chi_tiet_may_chuong_3_he_banh_rang_nguye.pdf

