Using the finite - time disturbance observer (FTO) for robotic manipulator Almega 16

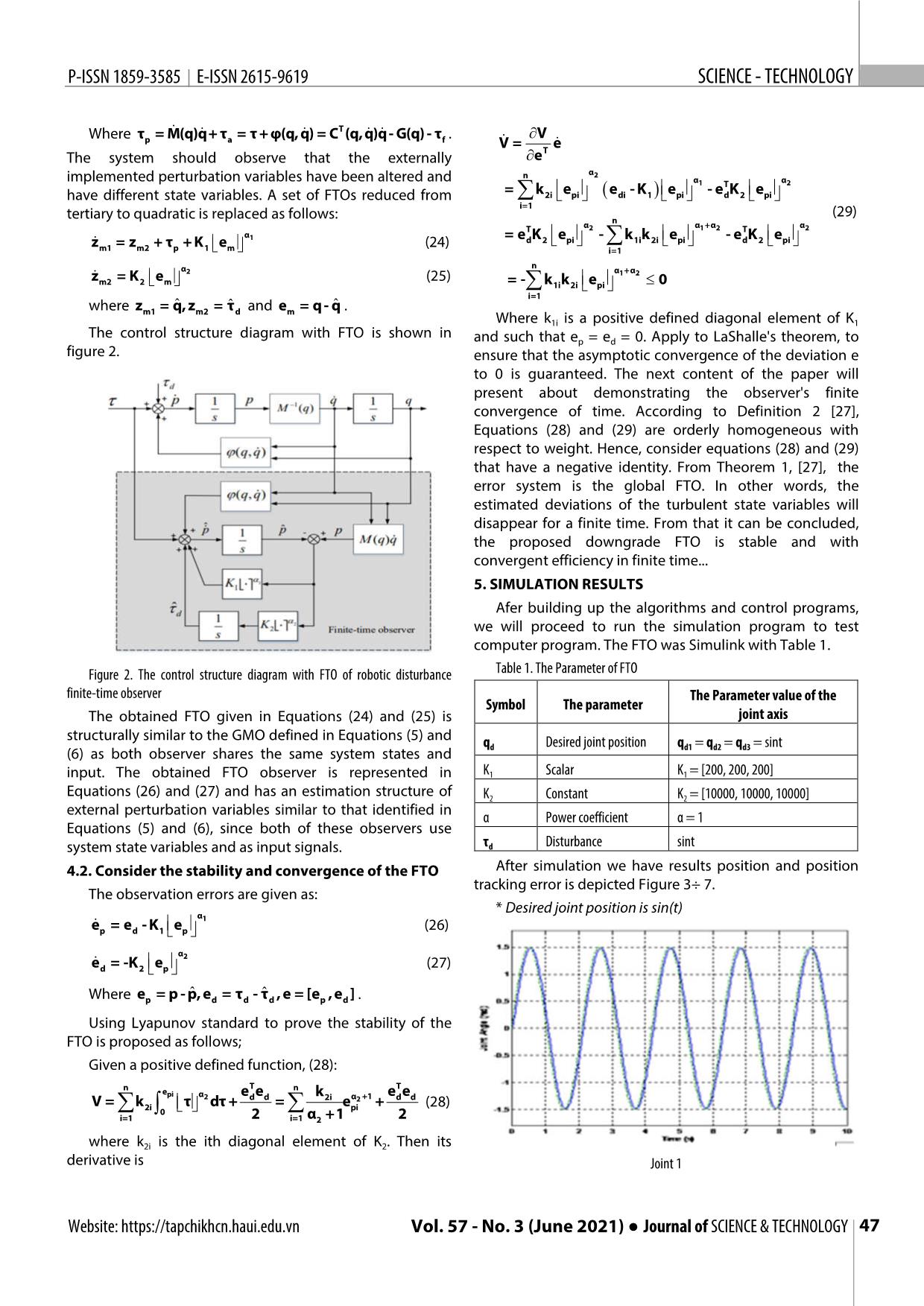
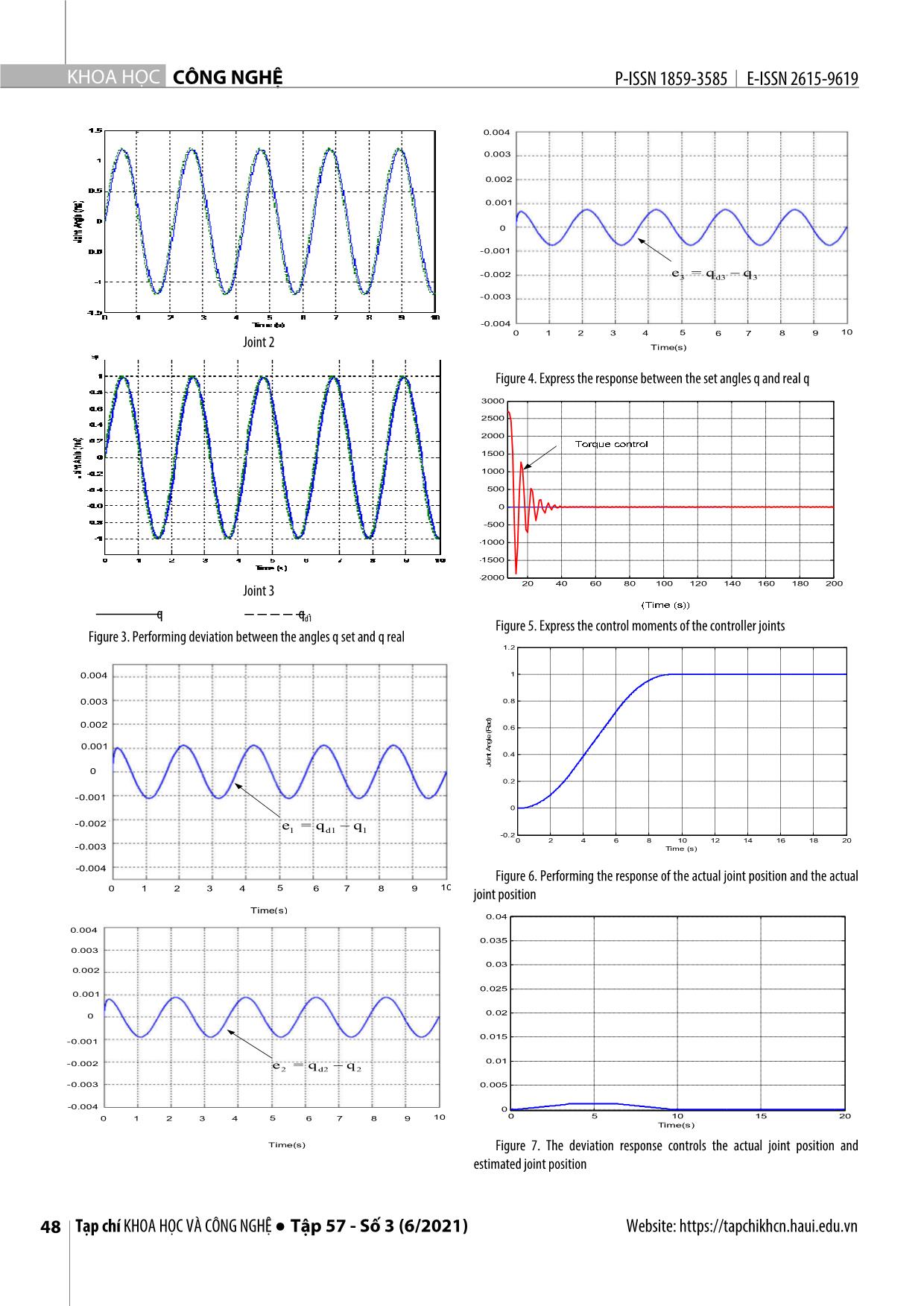
irst three joints have fully integrated the dynamics of the 
freedom arm. The motor connected to the joint is usually a The GMO component p is estimated as follows: 
 Website: https://tapchikhcn.haui.edu.vn Vol. 57 - No. 3 (June 2021) ● Journal of SCIENCE & TECHNOLOGY 45
 KHOA H ỌC CÔNG NGHỆ P-ISSN 1859-3585 E-ISSN 2615-9619 
 pˆ = τ +CT (q,q)q-   G(q)+ τˆ (5)  -1 α2
 d zb2 = z b3 + M (q)τ a +K 2 e b (14) 
 τˆ = K (p - p)ˆ (6) α3
 d 0 
 zb3 = K 3 e b (15) 
 where ( . )denotes the estimated value and 
 ˆ ˆ -1
 Where zb1 = q,ˆ z b2 = q, z b3 = M (q)τ d and 
 K0 diag k 0i 0 . So the estimate of the external 
 ˆ nxn
 disturbance is given is: e=q-qK,K,Kb, 1 2 3 R are diagonal gain matrices. 
 ˆ T   ˆ (7) Moreover, the corresponding powers are selected as 
 τd = K 0 (τ + C (q,q)q- G(q)+ τ d )dt 
 2
 From equations (5) and (6), are determined: α1 =α,α 2 =2α-1,α 3 =3α-1 and < α < 1. The operator 
 3
 τˆ = K (τ - τˆ ) (8) α
 d 0 d d . is denoted as 
 or convert to a Laplace image which will be written in 
 α α n
 the following format: x = x sgn(x), x R and α > 0 (16) 
 K
 0 Consequently, the disturbance observation τˆ d is 
 τˆ d = τ d (9) 
 s +K0 computed as 
 According to reference [9] shows that the component τˆ d = M(q)z b3 (17) 
 τˆ is a first order inertial function τ . So the external 
 d d From (17) shows, the proposed FTO is a ternary system 
 perturbation estimation τˆ d component of the GMO will that can simultaneously estimate the joint velocity and the 
 converge exponentially and depend on the observation external perturbation component. It shows that the joint 
 matrix Ko. Therefore, the GMO observer always has an velocity can be obtained instantly from the robot control 
 estimated bias in the outer perturbations. system. From the formula (13) - (15), it is possible to 
 3.3. Consider steady state in finite time downgrade the observational equation for external 
 disturbance state variables leading to a reduction in the 
 Consider the following nonlinear system 
 computational heavy process. Therefore, the downgrade 
 x = f(x), x Rn ,f(0) = 0 (10) FTO is determined as follows: 
 where f satisfies the locally Lipschitz continuous  -1 α1
 zr1 = z r2 + M (q)τ a +K 1 e r (18) 
 condition. Some basic knowledge about finite time 
  α2
 homogeneity and stability (FTS) in the document [22,23]. zr2 = K 2 e r (19) 
 4. FINITE-TIME OBSERVER OF ROBOTIC DISTURBANCE -1
 Where zb1 = q,zˆ b2 = M (q)τ d and 
 The main content of this paper is to design a finite time 1
 observer so that the observation of the noise td can e = q- q,ˆ α = α, α = 2α -1, < α < 1. From formula (19), 
 b 1 2 2
 converge to its true value in a finite time. In this section 4 
 we determine the formula to calculate the estimate of the 
 will be presented on the content of constructing the FTO 
 external disturbance is determined as follows: 
 observer to estimate the external perturbations. After the 
 ˆ
 estimation is complete, the state variables estimate the τd M(q)z r2 (20) 
 external perturbations to the existing control system such The decremented FOT observer will estimate the 
 as the PID controller,.... When the FTO Observer is perturbed state variables faster than the original 
 connected, the calculation and elimination will be reduced. unremarked design. And from formula (12) shows that still 
 remove the inverse inertial matrix in the kinetic equation. exists the inverse matrix component of M(q). To remove 
 4.1. Finite-Time Observer Design the inverse inertial matrix component of M(q), it is 
 From Equation (1), the acceleration q can be written as necessary to rearrange the original system from equation 
 (12) into a transformed equation with different state 
  1 1  
 q= M (q)τd M (q)(τ C(q,q)q- G(q) - τ f ) (11) variables. Multiplying both sides of Equation (12) by M(q) 
   yields the following: 
 Put: τa = τ - C(q, q)q- G(q) - τ f , then (11) is rewritten as 
 M(q)q = τ + τ (21) 
 follows as: a d
 q = M-1 (q)τ +M -1 (q)τ (12) Additionally, the left side of Equation (21) could be 
 d a altered using the generalized momentum p, namely 
 -1
 where M (q)τd is treated as the system disturbances  
 p - M(q)q = τa + τ d (22) 
 with M-1 (q)τ the system input. According to reference 
 a Reorganizing Equation (22) and employing Property 1, 
 [20], the FTO monitor for manipulators is specifically the derivative of the generalized momentum p is rewritten 
 designed as follows: as 
  α1 
 zb1 = z b2 +K 1 e b (13) p = τd + τ p (23) 
46 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 57 - Số 3 (6/2021) Website: https://tapchikhcn.haui.edu.vn 
 P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
 Where τ = M(q)q+  τ = τ +φ(q,q)  = CT (q,q)q-   G(q) - τ . V
 p a f  
 V =T e
The system should observe that the externally e
 n α2
implemented perturbation variables have been altered and α α
 1T 2
have different state variables. A set of FTOs reduced from = k2i e pi e di - K 1 e pi - e d K 2 e pi 
 i=1 (29) 
tertiary to quadratic is replaced as follows: n
 TTα2 α 1 +α 2 α 2
 α1 = e K e - k k e - e K e 
 z = z + τ + K e (24) d 2 pi  1i 2i pi d 2 pi 
 m1 m2 p 1 m i=1
 n
 α α +α
 z = K e 2 (25) 1 2
 m2 2 m = - k1i k 2i e pi 0
 i=1
 ˆ ˆ
 where zm1 = q, z m2 = τˆ d and em = q- q . 
 Where k1i is a positive defined diagonal element of K1 
 The control structure diagram with FTO is shown in 
 and such that ep = ed = 0. Apply to LaShalle's theorem, to 
figure 2. ensure that the asymptotic convergence of the deviation e 
 to 0 is guaranteed. The next content of the paper will 
 present about demonstrating the observer's finite 
 convergence of time. According to Definition 2 [27], 
 Equations (28) and (29) are orderly homogeneous with 
 respect to weight. Hence, consider equations (28) and (29) 
 that have a negative identity. From Theorem 1, [27], the 
 error system is the global FTO. In other words, the 
 estimated deviations of the turbulent state variables will 
 disappear for a finite time. From that it can be concluded, 
 the proposed downgrade FTO is stable and with 
 convergent efficiency in finite time... 
 5. SIMULATION RESULTS 
 Afer building up the algorithms and control programs, 
 we will proceed to run the simulation program to test 
 computer program. The FTO was Simulink with Table 1. 
 Figure 2. The control structure diagram with FTO of robotic disturbance Table 1. The Parameter of FTO 
finite-time observer The Parameter value of the 
 Symbol The parameter 
 The obtained FTO given in Equations (24) and (25) is joint axis 
structurally similar to the GMO defined in Equations (5) and q Desired joint position q = q = q = sint 
(6) as both observer shares the same system states and d d1 d2 d3
input. The obtained FTO observer is represented in K1 Scalar K1 = [200, 200, 200] 
Equations (26) and (27) and has an estimation structure of K2 Constant K2 = [10000, 10000, 10000] 
external perturbation variables similar to that identified in α Power coefficient α = 1
Equations (5) and (6), since both of these observers use 
system state variables and as input signals. τd Disturbance sint 
4.2. Consider the stability and convergence of the FTO After simulation we have results position and position 
 tracking error is depicted Figure 3÷ 7. 
 The observation errors are given as: 
 α * Desired joint position is sin(t) 
  1
 ep = e d -K 1 e p (26) 
 α
  2
 ed = -K 2 e p (27) 
 Where ep = p -p,eˆ d = τ d -τˆ d ,e=[e p ,e] d . 
 Using Lyapunov standard to prove the stability of the 
FTO is proposed as follows; 
 Given a positive defined function, (28): 
 nTT n
 epi α e ek e e
 V = k τ 2 dτ +d d =2i eα2 +1 + d d (28) 
 2i 0  pi
 i=12 i=1 α2 +1 2
 where k2i is the ith diagonal element of K2. Then its 
derivative is Joint 1 
 Website: https://tapchikhcn.haui.edu.vn Vol. 57 - No. 3 (June 2021) ● Journal of SCIENCE & TECHNOLOGY 47
 KHOA H ỌC CÔNG NGHỆ P-ISSN 1859-3585 E-ISSN 2615-9619 
 0.004
 0.003
 0.002
 0.001
 0
 -0.001
 -0.002 e = q q
 3e2 = d3q d2 3 q 2
 -0.003
 -0.004
 0 1 2 3 4 5 6 7 8 9 10
 Joint 2 Time(s)
 Figure 4. Express the response between the set angles q and real q 
 3000
 2500
 2000
 1500
 1000
 500
 0
 -500
 -1000
 -1500
 -2000
 Joint 3 20 40 60 80 100 120 140 160 180 200
 q q 
 d1 Figure 5. Express the control moments of the controller joints 
 Figure 3. Performing deviation between the angles q set and q real 
 1.2
 0.004 1
 0.003 0.8
 0.002 0.6
 0.001
 0.4
 Joint Angle (Rad) (Rad) Angle Joint
 0
 0.2
 -0.001
 0
 -0.002
 e1 = q d1 q 1
 -0.2
 0 2 4 6 8 10 12 14 16 18 20
 -0.003 Time (s)
 -0.004
 Figure 6. Performing the response of the actual joint position and the actual 
 0 1 2 3 4 5 6 7 8 9 10 joint position 
 Time(s)
 0.04
 0.004
 0.035
 0.003
 0.03
 0.002
 0.025
 0.001
 0 0.02
 0.015
 -0.001
 -0.002 0.01
 e2 = q d2 q 2
 -0.003 0.005
 -0.004 0
 0 1 2 3 4 5 6 7 8 9 10 0 5 10 15 20
 Time(s) 
 Time(s) Figure 7. The deviation response controls the actual joint position and 
 estimated joint position 
48 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 57 - Số 3 (6/2021) Website: https://tapchikhcn.haui.edu.vn 
 P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
 Comment: The simulation results of the real state and [11]. Haddadin S., De Luca A., Albu-Schäffer A., 2017. Robot collisions: A 
the above estimate prove that the synthesized FTO survey on detection, isolation, and identification. IEEE Trans. Robot, 33, 1292–
observer is correct, showing that the joints of the Almega 1312. 
16 robot are good with small setting time, less oscillation, [12]. Cho C.N., Kim J.H., Kim Y.L., Song J.B., Kyung J.H., 2012. Collision 
over-adjustment. detection algorithm to distinguish between intended contact and unexpected 
6. CONCLUSION collision. Adv. Robot, 26, 1825–1840. 
 The order reduction FTO has omitted acceleration and [13]. Mohammadi A., Tavakoli M., Marquez H.J., Hashemzadeh F., 2013. 
inverse matrix matrix, resulting in the FTO making the Nonlinear disturbance observer design for robotic manipulators. Control Eng. 
estimation deviations converge to 0 in a finite time. Pract., 21, 253–267. 
Although FTO has a more complex formula and thus the [14]. Nikoobin A., Haghighi R., 2009. Lyapunov-based nonlinear disturbance 
calculation time increases slightly compared to other observer for serial n-link robot manipulators. J. Intell. Robot. Syst., 55, 135–153. 
observers. The theory and simulation results show that [15]. Menard T., Moulay E., Perruquetti W., 2010. A global high-gain finite-
using the FTO observatory to estimate the perturbation time observer. IEEE Trans. Autom. Control, 55, 1500–1506. 
components outside the Almega 16 robot motion system 
 [16]. Lopez-Ramirez F., Polyakov A., Efimov D., Perruquetti W., 2018. Finite-
has ensured the real joint position closely follows the 
 time and fixed-time observer design: Implicit Lyapunov function approach. 
estimated joint position and ensures the actual matching 
 Automatica, 87, 52–60. 
position is closely related to the matching position with 
small error. [17]. Menard T., Moulay E., Perruquetti W., 2017. Fixed-time observer with 
 simple gains for uncertain systems. Automatica, 81, 438–446. 
 [18]. Shen Y., Xia X., 2008. Semi-global finite-time observers for nonlinear 
 systems. Automatica, 44, 3152–3156. 
 REFERENCES [19]. Shtessel Y.B., Shkolnikov I.A., Levant A., 2007. Smooth second-order 
 [1]. Pi Y., Wang X., 2010. Observer-based cascade control of a 6-DOF parallel sliding modes: Missile guidance application. Automatica, 43, 1470–1476. 
hydraulic manipulator in joint space coordinate. Mechatronics, 20, 648–655. [20]. Perruquetti W., Floquet T., Moulay E., 2008. Finite-time observers: 
 [2]. Sahabi M.E., Li G., Wang X., Li S., 2016. Disturbance Compensation Based Application to secure communication. IEEE Trans. Autom. Control, 53, 356–360. 
Finite-Time Tracking Control of Rigid Manipulator. Math. Probl. Eng. 2016, [21]. Siciliano B., Sciavicco L., Villani L., Oriolo G., 2010. Robotics: Modelling, 
2034795. Planning and Control. Springer Science & Business Media: Berlin/Heidelberg, 
 [3]. Chen W.H., Yang J., Guo L., Li S., 2016. Disturbance-observer-based Germany. 
control and related methods-An overview. IEEE Trans. Ind. Electron., 63, 1083– [22]. Bhat S.P., Bernstein D.S., 2000. Finite-time stability of continuous 
1095. autonomous systems. SIAM J. Control Optim., 38, 751–766. 
 [4]. Bona B., Indri M., 2005. Friction compensation in robotics: An overview. [23]. Bhat S.P., Bernstein D.S., 2005. Geometric homogeneity with 
In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, applications to finite-time stability. Math. Control. Signals Syst., 17, 101–127. 
Spain, pp. 4360–4367. 
 [24]. Bacciotti A., Rosier L., 2006. Liapunov Functions and Stability in Control 
 [5]. Chen W.H., Ballance D.J., Gawthrop P.J., O’Reilly J., 2000. A nonlinear Theory. Springer Science & Business Media: Berlin/Heidelberg, Germany. 
disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron., 47, 932–
938. [25]. Ha V. T, 2012. Some control solutions aim to improve the quality of 
 industrial hand motions. Ph.D. thesis, Hanoi University of Science and 
 [6]. Magrini E., Flacco F., De Luca A., 2015. Control of generalized contact Technology. 
motion and force in physical human-robot interaction. In Proceedings of the 2015 
IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, [26]. Neil M., Frank L.L., 2004. Robot Manipulator Control Theory and 
USA, pp. 2298–2304. Practice. Marcel Dekker. 
 [7]. Magrini E., De Luca A., 2016. Hybrid force/velocity control for physical [27]. Pengfei Cao, Yahui Gan, Xianzhong Dai, 2019. Finite-Time Disturbance 
human-robot collaboration tasks. In Proceedings of the 2016 IEEE/RSJ Observer for Robotic Manipulators.Sensors (Basel), 19(8):1943. doi: 
International Conference on Intelligent Robots and Systems (IROS), Daejeon, 10.3390/s19081943. 
Korea, pp. 857–863. 
 [8]. Gaz C., Magrini E., De Luca A., 2018. A model-based residual approach for 
human-robot collaboration during manual polishing operations. Mechatronics 55, THÔNG TIN TÁC GIẢ 
234–247. 
 Võ Thu Hà 
 [9]. De Luca A., Mattone R., 2003. Actuator failure detection and isolation 
 Trường Đại học Kinh tế - Kỹ thuật Công nghiệp 
using generalized momenta. In Proceedings of the IEEE International Conference 
on Robotics and Automation, Taipei, Taiwan, Volume 1, pp. 634–639. 
 [10]. Ren T., Dong Y., Wu D., Chen K., 2018. Collision detection and 
identification for robot manipulators based on extended state observer. Control 
Eng. Pract., 79, 144–153. 
 Website: https://tapchikhcn.haui.edu.vn Vol. 57 - No. 3 (June 2021) ● Journal of SCIENCE & TECHNOLOGY 49