Kinematics modeling analysis of the geostationary satellite monitoring antenna system

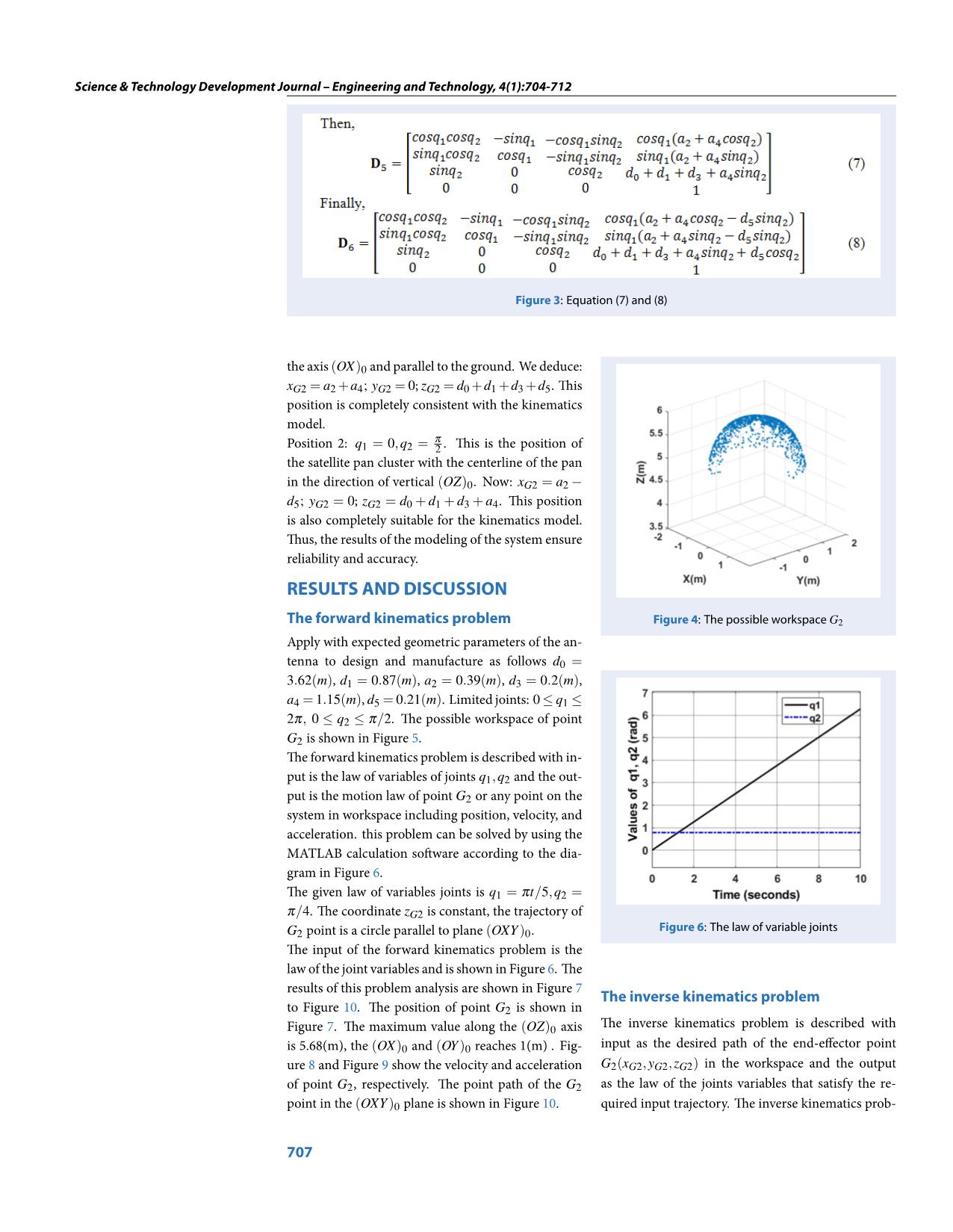
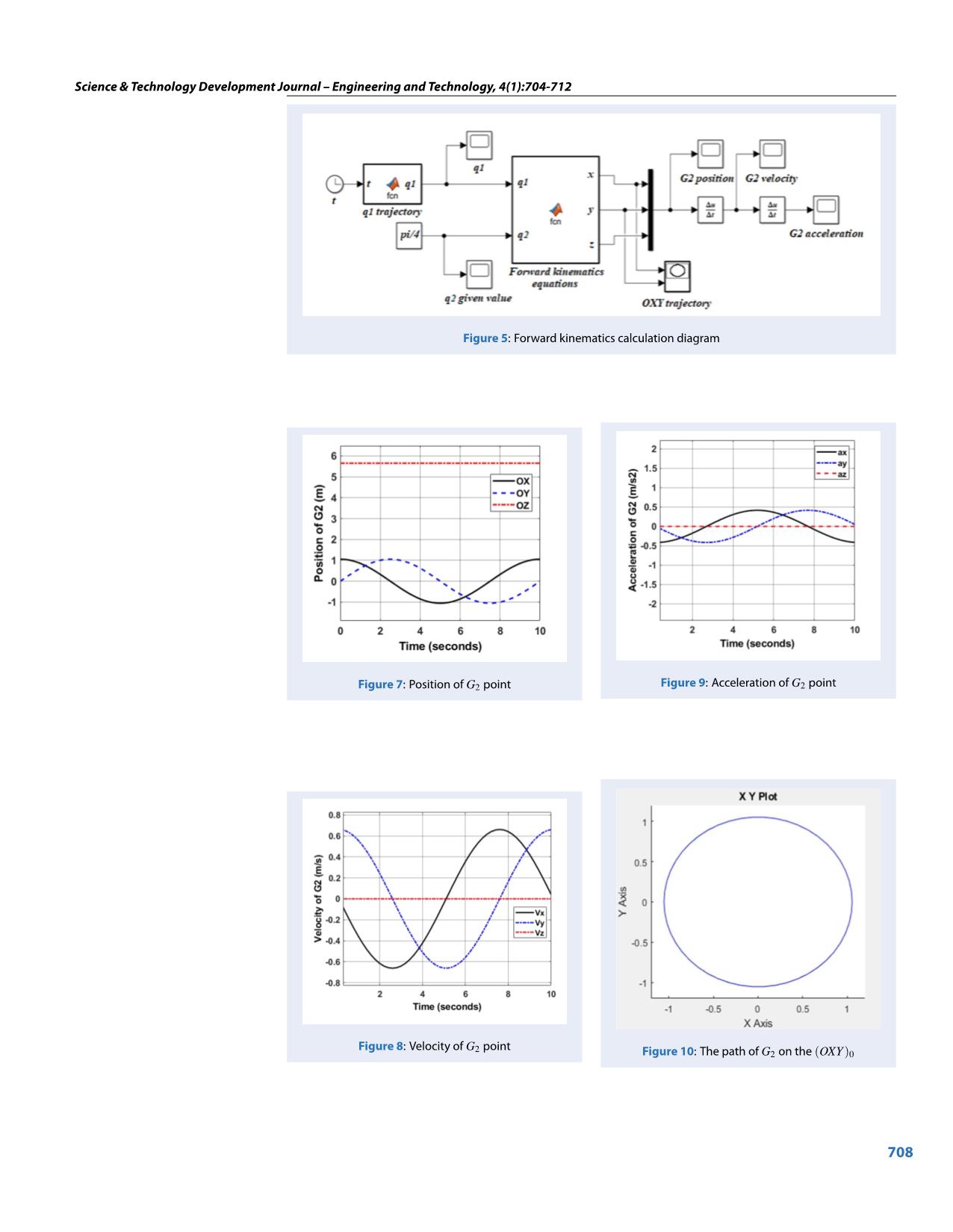
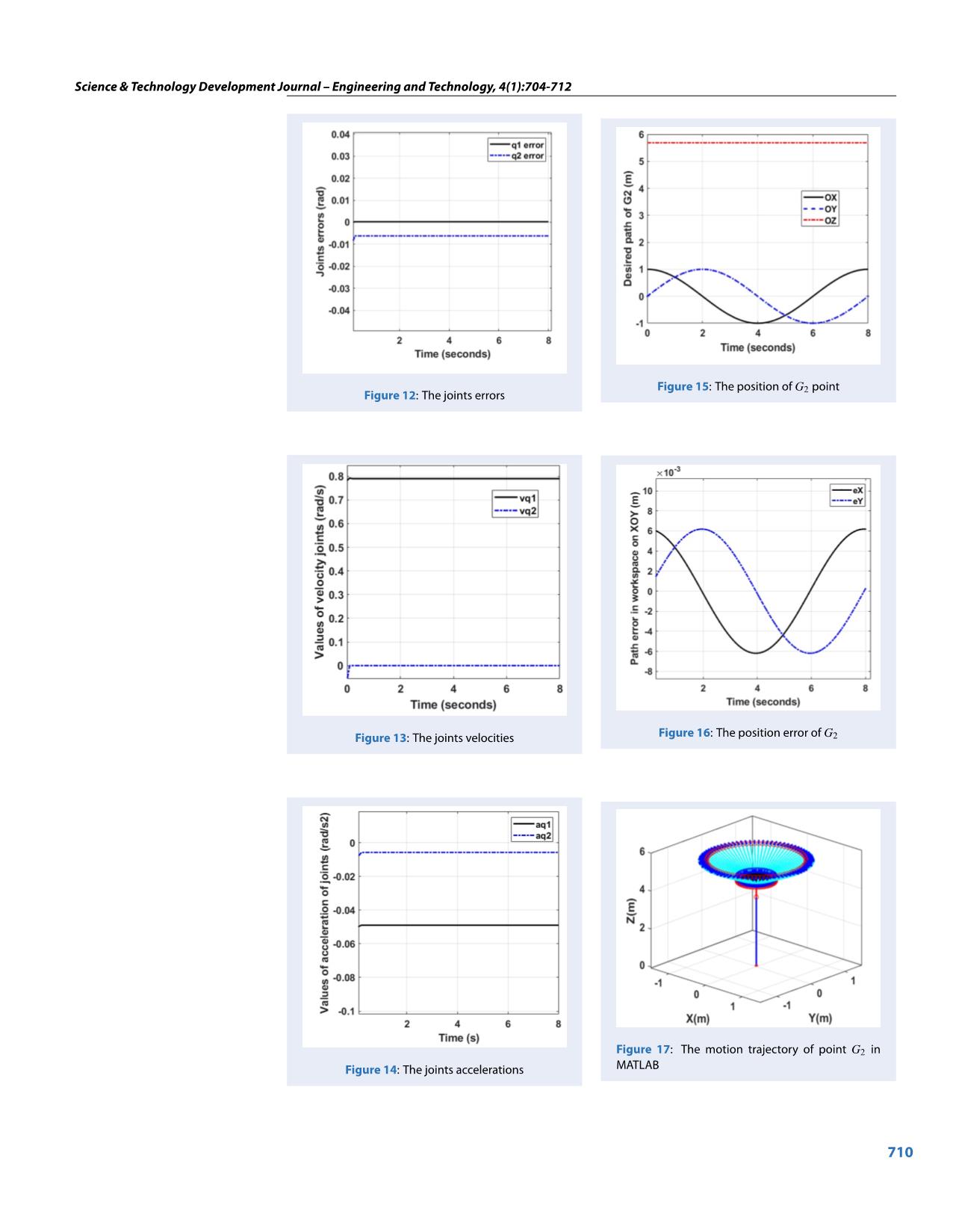
d cosq
   G2 0 1 3 4 2 5 2
 0 1 0 0 
 H =   Operate an inspection at a number of special loca-
 6 0 0 1 d 
 5 tions.
 0 0 0 1
 Position 1: q1 = q2 = 0. This is the position where the
 From local D-H matrices, the position of the (OXYZ)i direction cluster is in a stationary position. The cen-
 coordinate system compared to the fixed coordinate terline passes through the basin of the pan parallel to
 706
Science & Technology Development Journal – Engineering and Technology, 4(1):704-712
 Figure 3: Equation (7) and (8)
 the axis (OX)0 and parallel to the ground. We deduce:
 xG2 = a2 +a4; yG2 = 0; zG2 = d0 +d1 +d3 +d5. This
 position is completely consistent with the kinematics
 model.
 π
 Position 2: q1 = 0,q2 = 2 . This is the position of
 the satellite pan cluster with the centerline of the pan
 in the direction of vertical (OZ)0. Now: xG2 = a2 −
 d5; yG2 = 0; zG2 = d0 + d1 + d3 + a4. This position
 is also completely suitable for the kinematics model.
 Thus, the results of the modeling of the system ensure
 reliability and accuracy.
 RESULTS AND DISCUSSION
 The forward kinematics problem Figure 4: The possible workspace G2
 Apply with expected geometric parameters of the an-
 tenna to design and manufacture as follows d0 =
 3.62(m), d1 = 0.87(m), a2 = 0.39(m), d3 = 0.2(m),
 a4 = 1.15(m), d5 = 0.21(m). Limited joints: 0 ≤ q1 ≤
 2π, 0 ≤ q2 ≤ π/2. The possible workspace of point
 G2 is shown in Figure 5.
 The forward kinematics problem is described with in-
 put is the law of variables of joints q1,q2 and the out-
 put is the motion law of point G2 or any point on the
 system in workspace including position, velocity, and
 acceleration. this problem can be solved by using the
 MATLAB calculation software according to the dia-
 gram in Figure 6.
 The given law of variables joints is q1 = πt/5,q2 =
 π/4. The coordinate zG2 is constant, the trajectory of
 G2 point is a circle parallel to plane (OXY)0. Figure 6: The law of variable joints
 The input of the forward kinematics problem is the
 law of the joint variables and is shown in Figure 6. The
 results of this problem analysis are shown in Figure 7
 The inverse kinematics problem
 to Figure 10. The position of point G2 is shown in
 Figure 7. The maximum value along the (OZ)0 axis The inverse kinematics problem is described with
 is 5.68(m), the (OX)0 and (OY)0 reaches 1(m) . Fig- input as the desired path of the end-effector point
 ure 8 and Figure 9 show the velocity and acceleration G2(xG2,yG2,zG2) in the workspace and the output
 of point G2, respectively. The point path of the G2 as the law of the joints variables that satisfy the re-
 point in the (OXY)0 plane is shown in Figure 10. quired input trajectory. The inverse kinematics prob-
 707
Science & Technology Development Journal – Engineering and Technology, 4(1):704-712
 Figure 5: Forward kinematics calculation diagram
 Figure 7: Position of G2 point Figure 9: Acceleration of G2 point
 Figure 8: Velocity of G2 point
 Figure 10: The path of G2 on the (OXY)0
 708
Science & Technology Development Journal – Engineering and Technology, 4(1):704-712
 lem can be solved using either the analytical method The derivative of the two-sided derivative (12) respect
 or the numerical method. On the one hand, the an- to time
 alytic method allows us to use the kinematics equa- .. .. . .
 x(t) = J(q)q(t) + J (q)q(t) (16)
 tion transforms (9) to find q1,q2. However, the solv-
 ing process will encounter transcendent trigonomet- From (16)
 ric functions, so there are many satisfying results. The
 .. .. . .
 problem of choosing the right answer to the system J (q)q(t) = x(t) − J(q)q(t) (17)
 configuration is not a simple problem and takes a lot
 Put (15) into (17)
 of time. Sometimes this approach is not feasible for
 .. .. . .
 complex systems. On the other hand, the numeri- J (q)q(t) = x(t) − J(q)J+(q)x(t) (18)
 cal method uses modern algorithms to solve prob-
 lems according to the approximation method. The Then the joints acceleration vector can be written as
 .. .. . .
 outstanding advantage of this method is the feasibil- q(t) = J+ (q)x(t) − J+ (q)J (q)J+ (q)x(t) (19)
 ity and response to the requirements of the system
 configuration, which can solve complex problems that The velocity and acceleration vectors can be calculated
 the analytical method cannot meet. The limitations of from Eq. (15) and Eq. (19) if know q(t) at the time of
 . ..
 the numerical method are errors. However, with the investigation and x(t),x(t),x(t).
 strong development of computer science and mathe- Consider the desired motion of point G2 as follows
 matics, this problem is almost completely solved com- π
 xG2 = cos t (m);
 pared to the requirement of the problem. The algo- π4
 rithm of adjusting the generalized vector 14–17 is ap- y = sin t (m); (20)
 G2 4
 plied to solve this problem. zG2 = 5.68 (m)
 To facilitate the presentation of the generalized prob-
 lem, some vectors are defined as follows Operate the inverse kinematics problem in MATLAB
 [ ]
 T software, the results of this problem are described in
 x(t) = xG2 yG2 zG2 ; Figure 11 to Figure 16. The values of variables joints
 [ ] (10)
 T are shown in Figure 11. The joints errors are presented
 q(t) = q1 q2 qn
 in Figure 12. The velocity and acceleration of joints
 Relationship between coordinates of G2 point in the also described in Figure 13 and Figure 14, respec-
 workspace and joints coordinates in the joint space tively. The position of end-effector point G2 can be re-
 can be described as follows calculated through the forward kinematics equations
 with received q(t) is shown in Figure 15 with small
 x = f (q) (11)
 position error which is presented in Figure 16. The
 The derivative of the two-sided derivative (11) respect 3D model of antenna system (Figure 17) can be simu-
 to time lated in the MATLAB software by using the results of
 . ∂ f . . the inverse kinematics problem.
 x = q = J (q)q (12)
 ∂q
 where,
  
 ∂ f1 ∂ f1 ∂ f1
  ... 
  ∂q ∂q ∂q 
 ∂ f  1 2 n 
 J (q) = ∂ =  ... ... ... ...  (13)
 q  ∂ f ∂ f ∂ f 
 3 3 ... 3
 ∂q1 ∂q2 ∂qn
 The matrix J(q) of size 3xn is called a Jacobi matrix.
 For the redundant system, it is common to choose the
 pseudo-inverse matrix of the rectangular matrix J(q)
 as
 [ ]−
 J+ (q) = JT (q) J (q)JT (q) 1 (14)
 Then from the expression (14), the joints velocity is Figure 11: The positions of joints
 determined as
 . .
 q(t) = J+ (q)x(t) (15)
 709
Science & Technology Development Journal – Engineering and Technology, 4(1):704-712
 Figure 15: The position of G2 point
 Figure 12: The joints errors
 Figure 13: The joints velocities Figure 16: The position error of G2
 Figure 17: The motion trajectory of point G2 in
 Figure 14: The joints accelerations MATLAB
 710
Science & Technology Development Journal – Engineering and Technology, 4(1):704-712
 The dynamics equation and control system problems DUONG implemented research methods, calculated
 has been built and solved based on the results of the the program and drafted the manuscript.
 kinematics modeling analysis above. Figure 18 shows REFERENCES
 the entire antenna system fabricated and is in the pro-
 1. Maral G. Satellite communications systems - Systems, Tech-
 cess of assembly. The details of this issue will be pre- niques and Technology, Fifth Edition. John Wiley and Sons,
 sented in the next studies in the near future. Ltd Publication. 2009;.
 2. Satcom and Antenna technologies division at www.cpii.com
 [Access: October 2020];.
 3. VincorTM Product Data and Specification Archives: www.catal
 og.vincor.com [Access: October 2020];.
 4. Hubble Space Telescope: www.nasa.gov [Access: October
 2020];.
 5. Featured SATCOM Products: www.satcom-services.com [Ac-
 cess: October 2020];.
 6. Antenna Systems: www.viasat.com/products/antenna-syste
 ms [Access: October 2020];.
 7. Satellite Communications equipment: www.digisat.org [Ac-
 cess: October 2020] ;.
 8. Bindi Y, Dong L. Dynamics analysis and control of a spacecraft
 Figure 18: Geostationary satellite surveillance an- mechanism with joint clearance and thermal effect. Precision
 tenna was fabricated Motion Systems: Modeling, Control, and Applications, Else-
 vier Inc. 2019;p. 163–215. Available from: https://doi.org/10.
 1016/B978-0-12-818601-5.00017-2.
 9. Ogundele DA, et al. Mathematical Modelling of Antenna Look
 Angles of Geostationary Communications Satellite Using Two
 Models of Control Stations, 3rd International Conference on
 CONCLUSIONS Advanced Computer Theor and Engineering (ICACTE). 2010;p.
 In conclusion, this paper presents the kinematics 236–240.
 10. Ogundele DA, et al. Model validation and analysis of an-
 modeling of antenna systems for geostationary satel- tenna look angles of a geostationary satellite, International
 lite communications and monitoring, with the fo- Conference on Computer Science and Automation Engineer-
 cus on analyzing the kinematics problems. The ing (CSAE), IEEE. 2012;p. 509–513. Available from: https://doi.
 org/10.1109/CSAE.2012.6272824.
 workspace, position, velocity and acceleration of the 11. Lida T. Satellite Communications Antenna Concepts and En-
 pan cluster center of mass are calculated by using the gineering, Handbook of Satellite Applications, Springer Sci-
 ence+Business Media New York. 2015;PMID: 25435485. Avail-
 limit value of joints and solving the forward kinemat-
 able from: https://doi.org/10.1007/978-1-4614-6423-5_18-3.
 ics problem. The rules of joints are determined en- 12. Shankar SG, Reddy KV. Design and Simulation of Horn An-
 suring the given trajectory of pan cluster center of tenna in x-Ku Band for Satellite Communications. Interna-
 tional Journal of Research in Science & Technology (IJRST).
 mass in the workspace through analyzing the inverse 2014;1(10).
 kinematics problem. The numerical simulation re- 13. Spong MW, Hutchinson S, Vidyasagar M. Robot modeling and
 sults kinematics were successfully applied in dynam- Control, First edition. New York, USA. 2001;.
 14. Khang NV. Dynamics of Multi-bodies. Hanoi Science and Tech-
 ics and control analyzing and in practice. nology Publishing House. 2007;.
 15. Khang NV, et al. Inverse kinematic and dynamic analysis
 CONFLICT OF INTEREST of redundant measuring manipulator BKHN-MCX-04. Vietnam
 Journal of Mechanics, VAST. 2010;32:15–26. Available from:
 All of authors have no conflict on interest in publish- https://doi.org/10.15625/0866-7136/32/1/313.
 ing of the paper 16. My CA, et al. Inverse Kinematics Analysis of Welding Robot
 IRB 1520ID Using Algorithm for Adjusting the Increments of
 AUTHOR CONTRIBUTION Generalized Vector. The 5th International Conference on Re-
 search in Intelligent and Computing in Engineering. Springer
 Quoc-Hoang PHAM proposed ideas, research Singapore. 2020;Available from: https://doi.org/10.1007/978-
 981-15-7527-3.
 methods, quality monitoring and correcting the 17. Bien DX, et al. Optimize the Feed Rate and Determine the
 manuscript. Xuan-Hung LE, Manh-Tung DO, Joints Torque for Industrial Welding Robot TA 1400 Based
 Tai-Hoai Thanh NGUYEN, Hong-Phong NGUYEN, on Kinematics and Dynamics Modeling, International Journal
 of Mechanical Engineering and Robotics Research (IJMERR).
 Van-Tuan PHAM, and Tien-Trung VUONG de- 2020;9(9):1335–1340. Available from: https://doi.org/10.
 signed and fabricated the system. Xuan-Bien 18178/ijmerr.9.9.1335-1340.
 711
Tạp chí Phát triển Khoa học và Công nghệ – Kĩ thuật và Công nghệ, 4(1):704-712
 Open Access Full Text Article Bài nghiên cứu
Phân tích mô hình động học hệ thống Anten giám sát vệ tinh địa
tĩnh
Phạm Quốc Hoàng, Lê Xuân Hùng, Đỗ Mạnh Tùng, Nguyễn Tài Hoài Thanh, Nguyễn Hồng Phong,
Vương Tiến Trung, Phạm Văn Tuân, Dương Xuân Biên*
 TÓM TẮT
 Xu hướng phát triển khoa học trong tương lai không thể không kể đến sức ảnh hưởng to lớn của
 lĩnh vực không gian vũ trụ, trước mắt là các hệ thống vệ tinh liên quan đến công nghệ viễn thông.
 Use your smartphone to scan this Trên thực tế, ở một số nước có nền công nghệ thông tin liên lạc và công nghệ vũ trụ phát triển
 QR code and download this article mạnh mẽ thì vấn đề thiết kế, chế tạo hệ thống cơ khí anten giám sát vệ tinh địa tĩnh chắc chắn đã
 được giải quyết triệt để. Tuy nhiên, vì là một công nghệ đặc thù nên việc chia sẻ và chuyển giao
 công nghệ thiết kế và chế tạo cho các nước đang phát triển không hề dễ dàng. Hầu như rất khó tìm
 thấy các công trình đã công bố liên quan đến tính toán thiết kế cơ khí và chế tạo hệ thống anten
 giám sát vệ tinh địa tĩnh. Vấn đề chủ động nắm bắt công nghệ, từng bước tự chủ công nghệ chế
 tạo thiết bị viễn thông liên quan đến công nghệ vũ trụ luôn là mục tiêu của các nước đang phát
 triển như Việt Nam quan tâm và hướng tới nhằm hạn chế sự phụ thuộc công nghệ, giảm thiểu chi
 phí trang bị, chuyển giao công nghệ, đảm bảo bí mật quốc gia. Bước đầu tiên trong những vấn đề
 này là việc chủ động tự nghiên cứu thiết kế và chế tạo các thiết bị thu phát trên mặt đất như anten
 giám sát vệ tinh địa tĩnh.
 Bài báo này trình bày việc phân tích mô hình động học cho hệ thống anten giám sát vệ tinh địa
 tĩnh. Mỗi thành phần của hệ thống anten được giả thiết là vật rắn tuyệt đối. Mô hình toán học
 được xây dựng dựa trên lý thuyết động học và động lực học hệ nhiều vật. Phương pháp ma trận
 chuyển đổi thuần nhất DENAVIT-HARTENBERG (D-H) được sử dụng để xây dựng các phương trình
 động học. Bài toán động học thuận được phân tích để xác định vị trí, vận tốc, gia tốc và không
 gian làm việc của hệ thống anten với các giới hạn chuyển động góc của hệ thống đã cho. Bài toán
 động học ngược được đề cập để xác định các ứng xử động học của hệ thống anten với quỹ đạo
 chuyển động cho trước trong không gian làm việc. Kết quả tính toán và mô phỏng số động học
 đã được ứng dụng thành công trong thực tế, đặc biệt là ứng dụng để phân tích bài toán động lực
 học và bài toán điều khiển cho hệ thống anten vệ tinh địa tĩnh.
 Trung tâm Công nghệ, Đại học Kỹ thuật Từ khoá: Vệ tinh địa tĩnh, hệ thống anten, mô hình hóa, động học
 Lê Quý Đôn, 236 Hoàng Quốc Việt, Bắc
 Từ Liêm, Hà Nội, Việt Nam
 Liên hệ
 Dương Xuân Biên, Trung tâm Công nghệ,
 Đại học Kỹ thuật Lê Quý Đôn, 236 Hoàng
 Quốc Việt, Bắc Từ Liêm, Hà Nội, Việt Nam
 Email: duongxuanbien@lqdtu.edu.vn
 Lịch sử
 • Ngày nhận: 19-09-2020
 • Ngày chấp nhận: 05/03/2021 
 • Ngày đăng: 15/03/2021
 DOI : 10.32508/stdjet.v4i1.770 
 Bản quyền
 © ĐHQG Tp.HCM. Đây là bài báo công bố
 mở được phát hành theo các điều khoản của
 the Creative Commons Attribution 4.0
 International license.
 Trích dẫn bài báo này: Hoàng P Q, Hùng L X, Tùng D M, Thanh N T H, Phong N H, Trung V T, Tuân P V, 
 Biên D X. Phân tích mô hình động học hệ thống Anten giám sát vệ tinh địa tĩnh. Sci. Tech. Dev. J. - 
 Eng. Tech.; 4(1):704-712.
 712