Giáo trình Toán rời rạc (Phần 2)
6.1. Các khái niệm cơ bản của lý thuyết đồ thị
Lý thuyết đồ thị là một lĩnh vực đã đ-ợc nghiên cứu từ lâu và có nhiều ứng
dụng hiện đại. Chẳng hạn, đồ thị có thể sử dụng để xác định các mạch vòng
trong vấn đề giải tích mạch điện. Chúng ta có thể phân biệt hai hợp chất hoá
học có cùng công thức phân tử nh-ng có cấu trúc khác nhau nhờ đồ thị. Chúng
ta cũng có thể xác định xem hai máy tính trong mạng có thể trao đổi thông tin
đ-ợc với nhau hay không nhờ mô hình đồ thị của mạng máy tính. Đồ thị với
các trọng số đ-ợc gán cho các cạnh của nó có thể dùng để giải các bài toán
nh- bài toán tìm đ-ờng đi ngắn nhất giữa hai thành phố trong một mạng giao
thông. Chúng ta cũng còn sử dụng đồ thị để giải các bài toán về lập lịch, thời
khoá biểu và phân chia kênh cho các đài truyền hình.
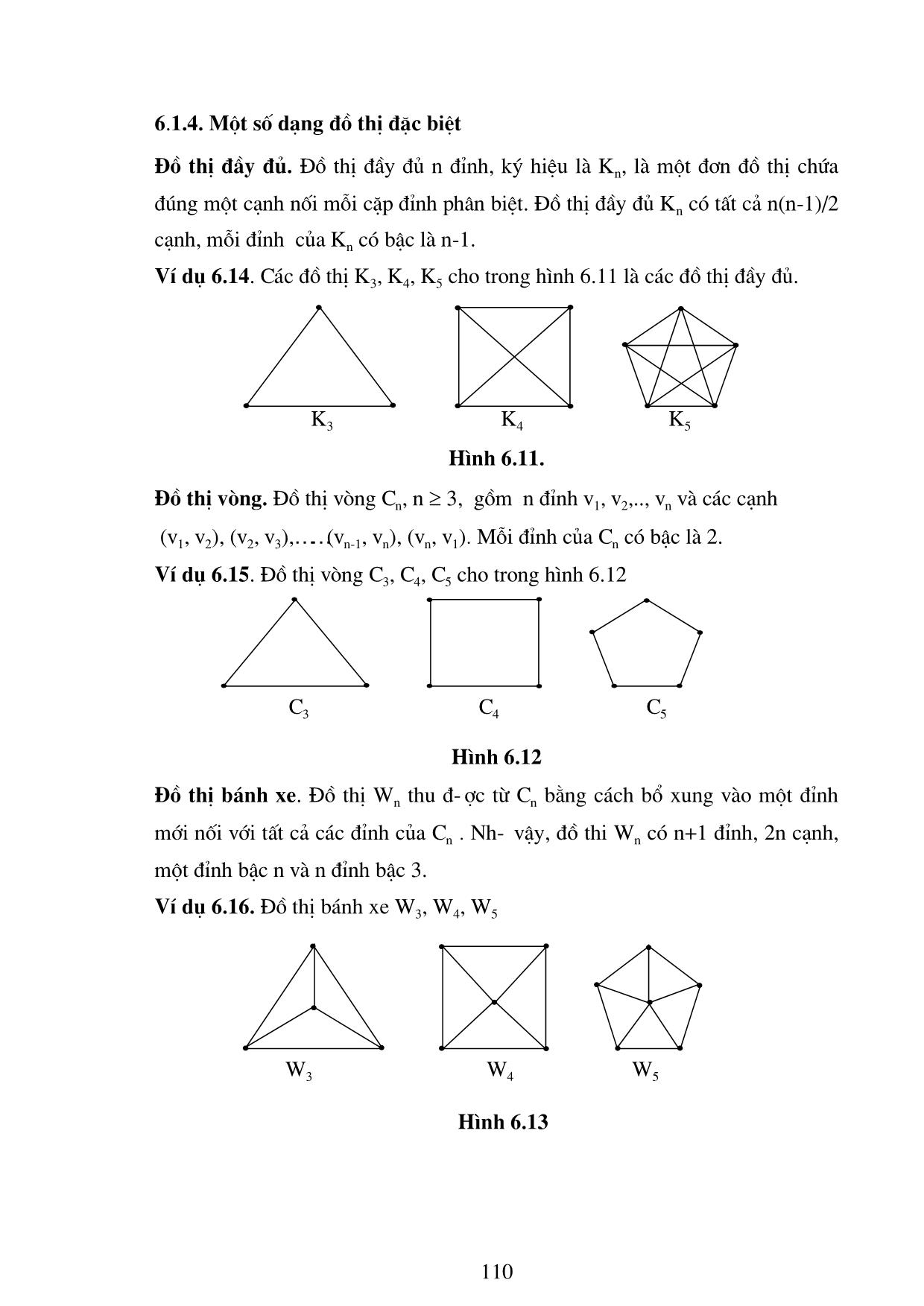
6.1.1. Định nghĩa đồ thị
Đồ thị là một cấu trúc rời rạc bao gồm các đỉnh và các cạnh nối các đỉnh
đó. Chúng ta phân biệt các loại đồ thị khác nhau bởi kiểu và số l-ợng cạnh nối
các cặp đỉnh của đồ thị.
Nhiều bài toán thuộc những lĩnh vực rất khác nhau có thể giải đ-ợc bằng
mô hình đồ thị. Chẳng hạn, ng-ời ta có thể dùng đồ thị để biểu diễn kết quả
của cuộc thi đấu thể thao. Chúng ta cũng sẽ chỉ ra rằng có thể dùng đồ thị để
giải các bài toán nh- bài toán tính số tổ hợp khác nhau của các chuyến bay
giữa hai thành phố trong một mạng hàng không, hay để giải bài toán ng-ời du
lịch, hoặc bài toán tìm số màu cần thiết để tô các vùng khác nhau của một bản
đồ,.
Định nghĩa 6.1. Đơn đồ thị vô h-ớng G = (V, E) bao gồm một tập không
rỗng V là tập các đỉnh, và một tập E là tập các cặp không có thứ tự gồm hai
phần tử khác nhau của V gọi là các cạnh.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Toán rời rạc (Phần 2)

các cung và luồng
giá trị 10 trong nó. Hai số viết bên cạnh mỗi cung là khả năng thông qua của
183
cung (số trong ngoặc ) và luồng trên cung .Đ•ờng tăng luồng có dạng
(s,v3,v 2 ,v 5 ,v 6 ,v 7 ,t) . ta tính đ•ợc (t)=1,giá trị luồng tăng từ 10 lên 11.
Hình 10.3(b) luồng thu đ•ợc sau khi tăng luồng theo đ•ờng tăng tìm đ•ợc.
6(6)
(a)
v v
2 0(2) 4 0(2) v6
4(4) 10(10)
0(3) 0(1)
4(5) 6(8)
t
s 4(9)
6(9) 0(2)
v5 v
v3 10(10) 4(4) 7
6(6)
(b)
v v
2 0(2) 4 0(2) v6
4(4) 10(10)
0(3) 1(1)
3(5) 5(8)
s t
3(9)
7(9) 1(2)
v5
v3 v7
10(10) 4(4)
Hình 10.3. Tăng luồng dọc theo đ•ờng tăng
Luồng trong hình 3(b) đã là cực đại. Lát cắt hẹp nhất
*
X = {s, v2, v3, v5 }, X = {v4, v6, v7, t }
Giá trị luồng cực đại là 11.
10.4. Một số bài toán luồng tổng quát
Trong phần này ta nêu một số bài toán về luồng tổng quát mà việc giải
chúng có thể dẫn về bài toán luồng cực đại trình bày ở trên.
a) Mạng với nhiều điểm phát và điểm thu
Xét mạng G với p điểm phát s 1 ,s 2 sp và q điểm thu f 1 ,f 2 fq.Gải sử rằng
luồng có thể đi từ một điểm phát bất kỳ đến tất cả các điểm thu. Bài toán tìm
luồng cực đại từ các điểm phát đến các điểm thu có thể đ•a về bài toán một
184
điểm phát và một điểm thu bằng cách đ•a vào một điểm phát giả s và một
điểm thu giả t và các cạnh nối s với tất cả các điểm phát và các cạnh nối t với
tất cả các điểm điểm thu.
Hình 10.4 minh hoạ cho cách đ•a mạng với nhiều điểm phát và nhiều
điểm thu về mạng chỉ có một điểm phát và một điểm thu . Khả năng thông qua
của các cung nối s với điểm phát sk sẽ bằng + nếu không có hạn chế về
l•ợng phát của điểm phát sk, và nếu l•ợng phát sk hạn chế bởi bk thì cung (s,sk)
có khả năng thông qua là bk. Cũng nh• vậy, đối với các cung nối tk với điểm
thu t, giá trị khả năng thông qua của(tk, t) sẽ là giới hạn hoặc không giới hạn
tuỳ theo l•ợng thu của điểm thu này có bị giới hạn hay không.
s t1
1
s s2
t2 t
sp
tq
Hình 10.4. Mạng với nhiều điểm phát và thu
Trường hợp một số điểm thu chỉ nhận ‚h¯ng ‚ từ một số điểm ph²t ta có b¯i
toán nhiều luồng là một bài toán phức tạp hơn rất nhiều so với bài toán luồng
cực đại giữa điểm phát s và điểm thu t.
b)Bài toán với khả năng thông qua của các cung và các đỉnh
Giả sử trong đồ thị G, ngoài khả năng thông qua của các cung c(u,v), ở mỗi
đỉnh v V còn có khả năng thông qua của đỉnh là d(v), và đòi hỏi tổng luồng
đi vào đỉnh v không đ•ợc v•ợt quá d(v), tức là
f (w,v) d(v)
w V
Cần phải tìm luồng cực đại giữa s và t trong mạng nh• vậy.
Xây dựng một m³ng G’ sao cho mỗi đỉnh v cða G tương ứng với hai đỉnh
v ,v- trong G’, mỗi cung (u,v) trong G t•ơng ứng với cung (u-, v ) trong G’.
Ngoài ra, mỗi cung (v ,v-) trong G’ có kh° năng thông qua l¯ d(v) ,tức l¯ b´ng
khả năng thông qua của đỉnh v trong G.
185
Do luồng đi vào đỉnh v phải đi qua cung (v+, v’) với kh° năng thông qua
d(v), nên luồng cực đ³i trong G’ sẽ b´ng luồng cực đ³i trong G với kh° năng
thông qua của các cung và các đỉnh.
c) Mạng trong đó khả năng thông qua của mỗi cung bị chặn hai phía
Xét mạng G mà trong đó mỗi cung (u,v) có khả năng thông qua (cận trên
của luồng trên cung) là c(u,v) và cận d•ới của luồng là d(u,v). Bài toán đặt ra
là liệu có tồn tại hay không luồng t•ơng thích từ s đến t ,tức là luồng {f(u,v):
u,v V} thoả mãn thêm ràng buộc
d(u,v) f(u,v) c(u,v) (u,v) E
Đ•a vào mạng G đỉnh phát giả sa, đỉnh thu giả ta và xây dựng mạng Ga theo
qui tắc:
Mỗi cung (u,v) mà d(u,v) 0 sẽ t•ơng ứng với hai cung(sa,v) và (u,ta) với
khả năng thông qua là d(u,v). Giảm c(u,v) đi d(u,v) tức là thay khả năng thông
qua của cung (u,v) bởi c(u,v) –d(u,v), còn cận d•ới của nó đặt bằng 0. Ngoài
ra thêm vào cung (t,s) với c(t,s) =
Hình 10.5 (a) cho ví dụ mạng G với khả năng thông qua của các cung bị
chặn cả hai phía. Đồ thị Ga t•ơng ứng đ•ợc cho trong hình 10.5(b).
u
a) 0,c(s,u) d(u,t),c(u,t)
s 0,c(u,v
) t
d(s,v),c(s,v)
0,c(v,t)
v
d(u,t)
ta
d(s,v) u c(u,t)-d(u,t)
c(s,u)
s d(u,v) t
b) c(s,v)-d(s,v)
c(v,t)
v d(u,t)
d(s,v)
Sa
Hình 10.5. Mạng với khả năng thông qua bị chặn hai phía
186
Ký hiệu d * = d(u,v) .
d (u,v) 0
Khi đó, ng•ời ta chứng minh đ•ợc rằng:
*
1) Nếu luồng lớn nhất trong mạng Ga từ sa đến ta bằng d thì tồn tại luồng
t•ơng thích trong G .
*
2) Nếu luồng lớn nhất trong mạng Ga từ sa đến ta là khác d thì không tồn
tại luồng t•ơng thích trong G
10.5. Một số ứng dụng trong tổ hợp
Bài toán luồng cực đại có rất nhiều ứng dụng trong việc giải nhiều bài
toán tổ hợp. Khó khăn chính ở đây là phải xây dựng mạng t•ơng ứng sao cho
việc tìm luồng cực đại trong nó sẽ t•ơng đ•ơng với bài toán tổ hợp đặt ra.
D•ới đây sẽ giới thiệu một số bài toán nh• vậy.
a) Bài toán đám c•ới vùng quê.
Có m chàng trai ở một làng quê nọ. Đối với mỗi chàng trai ta biết các cô
gái mà anh ta vừa ý. Hỏi khi nào có thể tổ chức các đám c•ới trong đó chàng
trai nào cũng sánh duyên với cô gái mà mình vừa ý.
Ta có thể xây dựng đồ thị với các đỉnh biểu thị các chàng trai và các cô
gái còn các cung biểu thị sự vừa ý của các chàng trai đối với các cô gái. Khi
đó ta thu đ•ợc một đồ thị hai phía.
Đ•a thêm vào điểm phát s và điểm thu t. Nối s với tất cả các đỉnh biểu thị
các chàng trai, và nối t với tất cả các đỉnh biểu thị các cô gái. Tất cả các cung
của đồ thị đều có khả năng thông qua bằng 1. Bắt đầu từ luồng 0, ta tìm luồng
cực đại trong mạng xây dựng đ•ợc theo thuật toán Ford – Fulkerson. Từ định
lý về tính nguyên, luồng trên các cung là các số 0 hoặc 1. Rõ ràng là nếu
luồng cực đại trong đồ thị có giá trị Vmax = m, thì bài toán có lời giải, và các
cung với luồng bằng 1 sẽ chỉ ra cách tổ chức đám c•ới thoả mãn điều kiện đặt
ra. Ng•ợc lại, nếu bài toán có lời giải thì Vmax = m.
b) Bài toán về hệ thống đại diện chung.
Cho tập m phần tử X = {z1, z2,,zm}. Giả sử và < B1,
B2,,Bn> là hai dãy các tập con của tập X. Dãy gồm n phần tử khác nhau của
X: đ•ợc gọi là hệ thống các đại diện chung của hai dãy đã cho
187
nếu nh• tìm đ•ợc một hoán vị của tập {1,2,,n} sao cho là hệ
thống các đại diện phân biệt của hai dãy và <B(1), B(2), ,
B(n)>, tức là điều kiện sau đ•ợc thoả mãn : ai Ai B(i) , i= 1,2,,n. Xây
dựng mạng G = (V,E) với tập đỉnh
V= {s,t} {x1, x2,, xn} {u1, u2,,um} {v1, v2,,vm} {y1, y2,,yn}
Trong đó đỉnh xi t•ơng ứng với tập Ai, đỉnh yi t•ơng ứng với tập Bi, các phần
tử ui, vi t•ơng ứng với phần tử zi. Tập các cung của mạng G đ•ợc xác định nh•
sau:
E = {(s,xi): 1 i n} {(xi, uj): với zj Ai, 1 i n, 1 j m}
{(uj, yj): 1 j m} {(vj, yj): với zi Bi, 1 i n, 1 j m}
{(yi, t): 1 i n}.
Khả năng thông qua của tất cả các cung đ•ợc đặt bằng 1 . Dễ dàng thấy rằng
hệ thống đại diện chung của hai dãy và tồn tại
khi và chỉ khi trong mạng G = (V,E) tìm đ•ợc luồng với giá trị n. Để xét sự tồn
tại của luồng nh• vậy có thể sử dụng thuật toán tìm luồng cực đại từ s đến t
trong mạng G = (V,E).
c) Một bài toán tối •u rời rạc
Trong mục này ta sẽ trình bày thuật toán đ•ợc xây dựng dựa trên thuật
toán tìm luồng cực đại để giải một bài toán tối •u rời rạc là mô hình toán học
cho một số bài toán tối •u tổ hợp.
Xét bài toán tối •u rời rạc
n
f (x1 , x2 ,..., xn ) max xij min (1)
1 i m
j 1
với điều kiện
n
aaij xij pi ,i 1,2,...,m, (2)
j 1
xij = 0 hoặc 1, j = 1, 2,, n (3)
Trong đó aij {0,1}, i = 1, 2,, m; j = 1, 2,, n, pi nguyên d•ơng, i= 1,
2,,m.
Bài toán (1)-(3) là mô hình toán học cho nhiều bài toán tối •u tổ hợp thực
tế. Ng•ời ta đã chứng minh đ•ợc rằng việc giải bài toán (1)-(3) có thể dẫn về
việc giải một số hữu hạn bài toán luồng cực đại trong mạng. D•ới đây là một
vài ví dụ về những bài toán có thể đ•a về bài toán (1)-(3).
Bài toán phân nhóm sinh hoạt. Có m sinh viên và n nhóm sinh hoạt chuyên
đề. Với mỗi sinh viên i, biết
aij = 1, nếu sinh viên i có nguyện vọng tham gia vào nhóm j
188
aij = 0, nếu ng•ợc lại
và pi là số l•ợng nhóm chuyên đề mà sinh viên i phải tham dự, i= 1,2,,m; j=
1,2,,n.
Trong số các cách phân các sinh viên vào các nhóm chuyên đề mà họ có
nguyện vọng tham gia và đảm bảo mỗi sinh viên i phải tham gia đúng pi
nhóm, hãy tìm cách phân phối với số ng•ời trong nhóm có nhiều sinh viên
tham gia nhất là nhỏ nhất có thể đ•ợc .
Đ•a vào biến số
xij = 1, nếu sinh viên i tham gia vào nhóm j
xij = 0, nếu ng•ợc lại
i= 1,2,, m, j = 1, 2,, n, khi đó mô hình toán học cho bài toán đặt ra chính là
bài toán (1)-(3).
Bài toán lập lịch cho hội nghị. Một hội nghị có m tiểu ban, mỗi tiểu ban cần
sinh hoạt trong một ngày tại phòng họp phù hợp với nó. Có n phòng họp dành
cho việc sinh hoạt của các tiểu ban. Biết
aij = 1, nếu phòng họp i là thích hợp với tiểu ban j
aij = 0, nếu ng•ợc lại,
i = 1, 2, , m; j = 1, 2,, n. Hãy bố trí các phòng họp cho các tiểu ban sao
cho hội nghị kết thúc sau ít ngày làm việc nhất.
Đ•a vào biến số
xij = 1, nếu bố trí tiểu ban i làm việc ở phòng j
xij = 0, nếu ng•ợc lại
i = 1, 2,, m, j = 1, 2,, n, khi đó dễ thấy mô hình toán học cho bài toán đặt
ra chính là bài toán (1) – (3), trong đó pi = 1, i = 1, 2,, m.
Ng•ời ta đã chứng minh đ•ợc rằng
n
Bài toán (1)-(3) có ph•ơng án tối •u khi và chỉ khi aij pi , i=1, 2,..., m
j 1
189
bài tập ch•ơng 10
1. Cho mạng nh• hình d•ới, với khả năng thông qua của các cung đ•ợc ghi
trong các vòng tròn, luồng (khởi đầu) đ•ợc ghi trên các cung. Hãy tìm luồng
cực đại của mạng
4 3
v1 v5
4 3
4 4
6
6
7
8
4
v2 2
5
5
12
v 1
s 5 6 t
1
5 4 3
8 v3
4
6 2 6
9
2
4
4 4
v4 v7
2. Cho mạng sau, với khả năng thông qua của các cung đ•ợc ghi trong các
vòng tròn. Tìm luồng cực đại của mạng.
6
v1 v5
2 4
4
8
2 4 2
s v3 v4 t
4 3
4
8
v2 v6
6
3. Cho mạng sau, với khả năng thông qua của các cung đ•ợc ghi trong các
vòng tròn, luồng (khởi đầu) đ•ợc ghi trên các cung. Tìm luồng cực đại của
mạng.
6 6
10
v1 v2
8 8 0 6
10 2 15
8 8 20 16
s v3 v4
28
16 10 3
4 6 0
6 3
2 30
15 10
5 0 v6 v7 25
v5 7
0 0
10 8 0 6 7
15
1 0
2 2
2 2 t
v8 4 v10
12 2
v9 20 0
190
MỤC LỤC
Chƣơng 1. MỘT SỐ KIẾN THỨC MỞ ĐẦU VỀ Lí THUYẾT TỔ HỢP
1.1. Giới thiệu về tổ hợp 2
1.2. Sơ lược về lý thuyết tập hợp 4
1.2.1. Cỏc khỏi niệm 4
1.2.2. Cỏc phộp toỏn 5
1.2.3. Cỏc tớnh chất cho trờn tập hợp 7
1.2.4. Quan hệ tương đương và phõn hoạch 7
1.2.5. Biểu diễn tập hợp trờn mỏy tớnh 8
1.3. Một số nguyờn lý cơ bản 9
1.3.1. Nguyờn lý cộng 9
1.3.2. Nguyờn lý nhõn 10
1.4. Cỏc cấu hỡnh tổ hợp đơn giản 11
1.4.1. Chỉnh hợp lặp 11
1.4.2. Chỉnh hợp khụng lặp 12
1.4.3. Hoỏn vị 13
1.4.4. Tổ hợp 13
Chƣơng 2. BÀI TOÁN ĐẾM
2.1. Giới thiệu bài toỏn 17
2.2. Nguyờn lý bự trừ 18
2.3. Qui về cỏc bài toỏn đơn giản 22
2.4. Cụng thức truy hồi 25
2.4.1. Cỏc vớ dụ minh họa 25
2.4.2. Giải cụng thức truy hồi tuyến tớnh thuần nhất hệ số hằng 27
2.5. Liệt kờ 31
Chƣơng 3. BÀI TOÁN TỒN TẠI
3.1. Giới thiệu bài toỏn 35
3.2. Phương phỏp phản chứng 38
3.3. Nguyờn lý Dirichlet 39
191
3.3.1. Giới thiệu nguyờn lý 39
3.3.2. Cỏc vớ dụ minh họa 40
3.4. Hệ đại diện phõn biệt 43
3.4.1. Khỏi niệm hệ đại diện phõn biệt 43
3.4.2. Định lớ Hall 44
Chƣơng 4: BÀI TOÁN LIỆT Kấ
4.1. Giới thiệu bài toỏn 48
4.2. Phương phỏp sinh 49
4.2.1. Giới thiệu thuật toỏn sinh 49
4.2.2. Cỏc vớ dụ 50
4.3. Thuật toỏn quay lui 57
4.3.1. Giới thiệu thuật toỏn 57
4.3.2. Cỏc vớ dụ 59
Chƣơng 5 : BÀI TOÁN TỐI ƢU
5.1. Giới thiệu bài toỏn 67
5.1.1. Phỏt biểu bài toỏn 67
5.1.2. Đưa bài toỏn tối ưu về dạng tổng quỏt 67
5.2. Cỏc thuật toỏn duyệt 71
5.2.1. Duyệt toàn bộ 71
5.2.2. Thuật toỏn nhỏnh cận 72
5.3. Thuật toỏn nhỏnh cận giải bài toỏn người du lịch 79
5.3.1. Thủ tục rỳt gọn 81
5.3.2. Thủ tục chọn cạnh phõn nhỏnh 84
5.3.3. Thuật toỏn nhỏnh cận giải bài toỏn người du lịch 89
5.4. Bài toỏn lập lịch gia cụng trờn hai mỏy. Thuật toỏn Jonhson 90
5.4.1. Bài toỏn lập lịch gia cụng trờn hai mỏy 90
5.4.2. Định lý Jonhson 93
5.4.3. Thuật toỏn Jonhson. 95
Chƣơng 6. CÁC KHÁI NIỆM CƠ BẢN CỦA Lí THUYẾT ĐỒ THỊ
192
BIỂU DIỄN ĐỒ THỊ TRấN MÁY TÍNH
6.1. Cỏc khỏi niệm cơ bản của lý thuyết đồ thị 100
6.1.1. Định nghĩa đồ thị 100
6.1.2. Cỏc thuật ngữ cơ bản 103
6.1.3. Đường đi, chu trỡnh. Đồ thị liờn thụng 105
6.1.4. Một số dạng đồ thị đặc biệt 108
6.2. Biểu diễn đồ thị trờn mỏy tớnh 109
6.2.1. Biểu diễn đồ thị bằng danh sỏch cạnh
111
6.2.2. Biểu diễn đồ thị bằng danh sỏch kề 112
6.2.3. Biểu diễn đồ thị bằng ma trận kề 113
6.2.4. Sự đẳng cấu của cỏc đồ thị 114
Chƣơng 7. CÁC THUẬT TOÁN TèM KIẾM TRấN ĐỒ THỊ
VÀ ỨNG DỤNG
7.1. Tỡm kiếm theo chiều sõu 121
7.1.1. Giới thiệu thuật toỏn 121
7.1.2. Vớ dụ minh họa 122
7.2. Tỡm kiếm theo chiều rộng 123
7.2.1. Giới thiệu thuật toỏn 123
7.2.2. Vớ dụ minh họa 124
7.3. Tỡm đường đi và kiểm tra tớnh liờn thụng
125
7.3.1. Bài toỏn tỡm đường đi giữa hai đỉnh 125
7.3.2. Tỡm cỏc thành phần liờn thụng 126
Chƣơng 8. ĐỒ THỊ EULER VÀ ĐỒ THỊ HAMILTON
8.1. Đồ thị Euler 130
8.1.1. Định nghĩa 130
8.1.2. Định lý Euler 131
8.1.3. Thuật toỏn Flor 133
8.2. Đồ thị Hamilton 134
193
8.2.1. Định nghĩa 135
8.2.2. Định lý (Dirak) 140
8.2.3. Thuật toỏn liệt kờ cỏc chu trỡnh Hamilton của đồ thị 141
Chƣơng 9. CÂY VÀ CÂY KHUNG CỦA ĐỒ THỊ
BÀI TOÁN ĐƢỜNG ĐI NGẮN NHẤT
9.1. Cõy và cỏc tớnh chất cơ bản 144
9.2. Cõy khung của đồ thị 147
9.3. Bài toỏn cõy khung nhỏ nhất 149
9.3.1. Thuật toỏn Kruskal 150
9.3.2. Thuật toỏn Prim 153
9.4. Bài toỏn đường đi ngắn nhất 158
9.4.1. Cỏc khỏi niệm 158
9.4.2. Đường đi ngắn nhất xuất phỏt từ một đỉnh 160
9.4.3. Thuật toỏn Dijkstra 163
9.4.4. Đường đi ngắn nhất giữa tất cả cỏc cặp đỉnh 168
Chƣơng 10. BÀI TOÁN LUỒNG CỰC ĐẠI TRONG MẠNG
10.1. Bài toỏn luồng cực đại 176
10.1.1. Khỏi niệm mạng 176
10.1.2. Luồng trong mạng 176
10.1.3. Bài toỏn luồng cực đại trong mạng 177
10.2. Lỏt cắt. Đường tăng luồng 177
10.2.1. Khỏi niệm lỏt cắt 177
10.2.2. Đường tăng luồng 179
10.3. Thuật toỏn tỡm luồng cực đại trong mạng 180
10.4. Một số bài toỏn luồng tổng quỏt 185
10.5. Một số ứng dụng trong tổ hợp 188
194
tài liệu tham khảo
[1]. KENNETH H. ROSEN. Toán rời rạc ứng dụng trong tin học. NXB Khoa học
và kỹ thuật. 2000
[2]. Hoàng Tụy. Đồ thị hữu hạn và các ứng dụng trong vật trù học. NXB Khoa
học, Hà Nội. 1964
[3]. Nguyễn Đức Nghĩa- Nguyễn Tô Thành. Toán rời rạc. NXB Giáo dục.
2003
[4]. Đặng Huy Ruận. Lý thuyết đồ thị và ứng dụng. Nhà xuất bản Khoa học và
kỹ thuật.2004
[5]. Đỗ Đức Giáo. Toán rời rạc. Nhà xuất bản Khoa học và kỹ thuật. 1999
[6]. Đại học Khoa học-Đại học Huế. Giáo trình Toán rời rạc. 2003
195 File đính kèm:
 giao_trinh_toan_roi_rac_phan_2.pdf
giao_trinh_toan_roi_rac_phan_2.pdf

