Bài giảng Toán rời rạc - Chương: Đường đi trên đồ thị (Version 0.2) - Trần Vĩnh Đức
Tìm kiếm theo chiều rộng (Breadth-First Search)
Chia đồ thị thành các mức:
▶ S là mức có khoảng cách 0.
▶ Các đỉnh có khoảng cách tới
S bằng 1.
▶ Các đỉnh có khoảng cách tới
S bằng 2
Algorithms 105
A physical model of a graph.
er hand, edge (D, E ) plays no role in any shortest path an

Trang 1

Trang 2

Trang 3
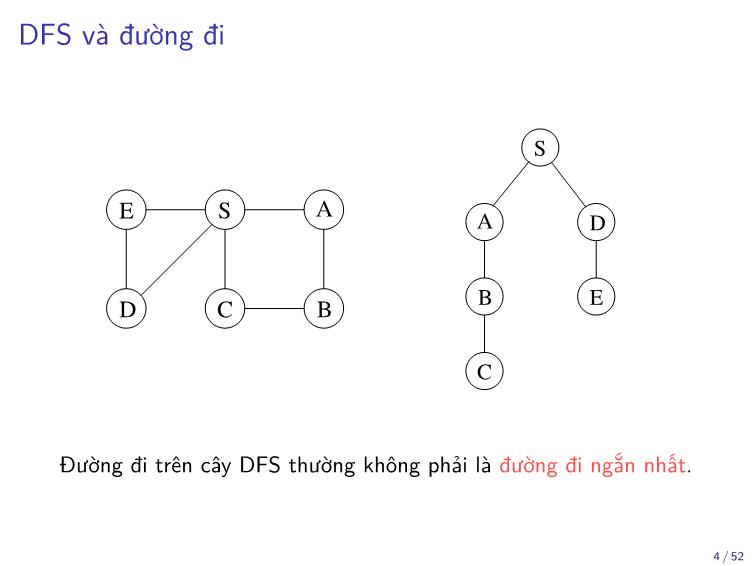
Trang 4
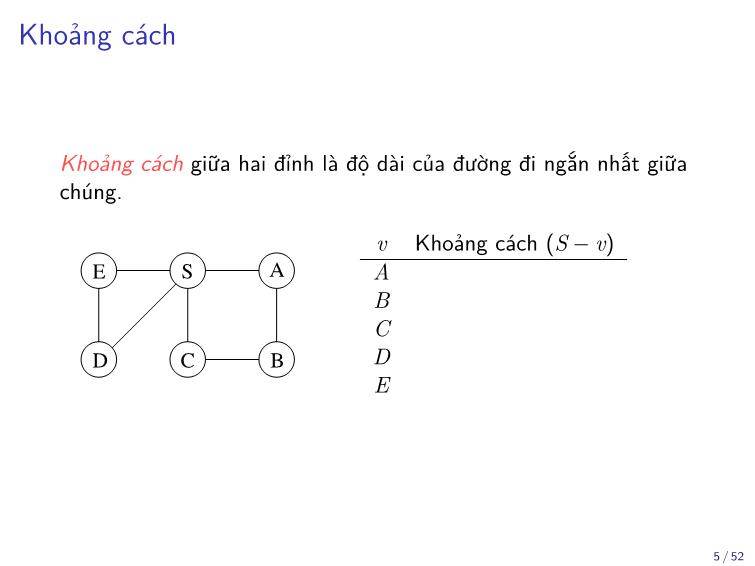
Trang 5
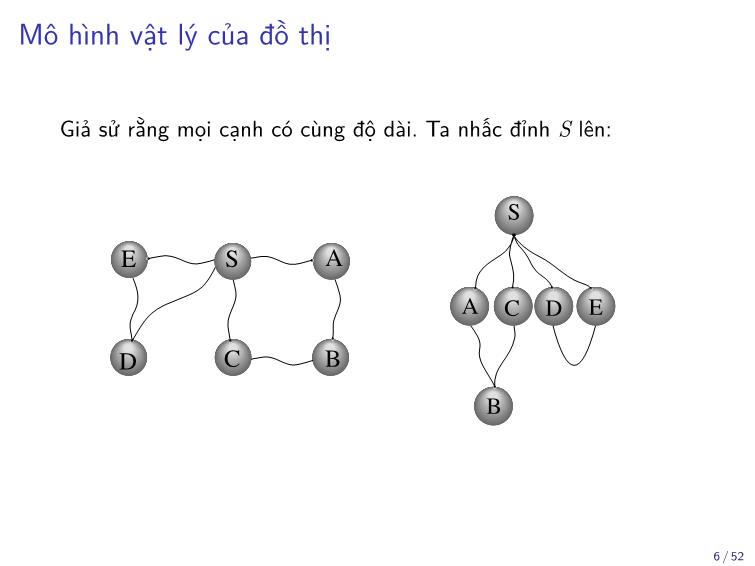
Trang 6
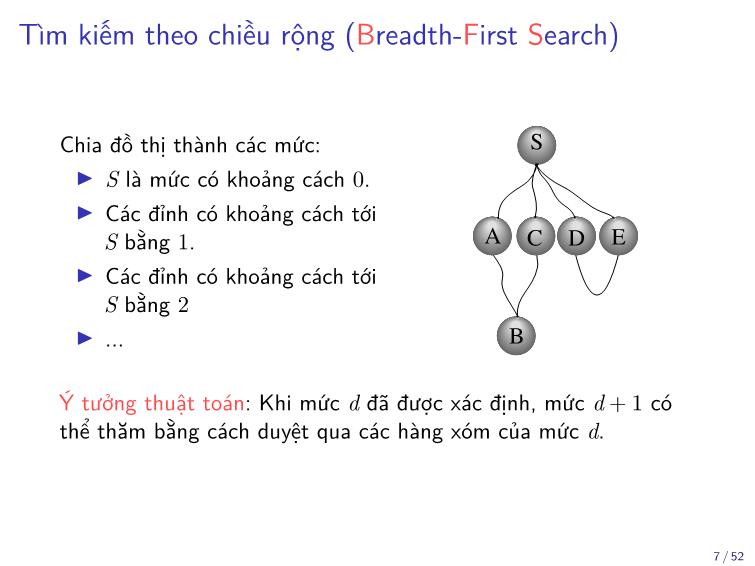
Trang 7

Trang 8
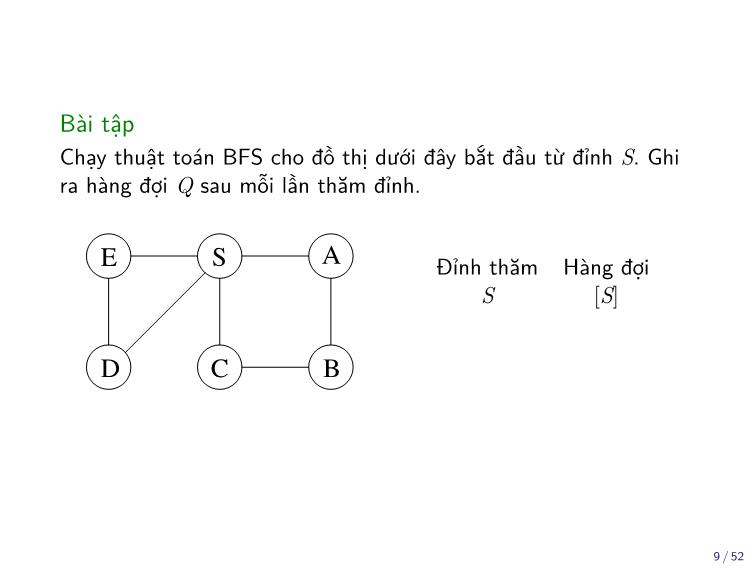
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương: Đường đi trên đồ thị (Version 0.2) - Trần Vĩnh Đức", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương: Đường đi trên đồ thị (Version 0.2) - Trần Vĩnh Đức

C E
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Ví dụ: Bước 1
Chapter 4 Algorithms 111
Figure 4.9 A complete run of Dijkstra’s algorithm, with node A as the starting
point. Also shown are the associated dist values and the final shortest-path tree.
2
B D
4
4 A: 0 D:
∞
A 13 1 B: 4 E:
∞
3 C: 2
2
E
C 5
2
B D
4
4
1 3 A: 0 D: 6
A 1 B: 3 E: 7
3
2 C: 2
C E
5 23 / 52
2
B D
4
4
A: 0 D: 5
A 13 1
B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
4
4 A: 0 D: 5
A 13 1 B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
A 1 3
2
C E
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms 111
Figure 4.9 A complete run of Dijkstra’s algorithm, with node A as the starting
point. Also shown are the associated dist values and the final shortest-path tree.
2
B D
Ví dụ: Bước4 2
4 A: 0 D:
∞
A 13 1 B: 4 E:
∞
3 C: 2
2
E
C 5
2
B D
4
4
1 3 A: 0 D: 6
A 1 B: 3 E: 7
3
2 C: 2
E
C 5
2
B D
4
4
A: 0 D: 5
A 13 1
B: 3 E: 6
3
2 C: 2
E 24 / 52
C 5
2
B D
4
4 A: 0 D: 5
A 13 1 B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
A 1 3
2
C E
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms 111
Figure 4.9 A complete run of Dijkstra’s algorithm, with node A as the starting
point. Also shown are the associated dist values and the final shortest-path tree.
2
B D
4
4 A: 0 D:
∞
A 13 1 B: 4 E:
∞
3 C: 2
2
E
C 5
2
B D
4
Ví dụ: Bước 3 4
1 3 A: 0 D: 6
A 1 B: 3 E: 7
3
2 C: 2
E
C 5
2
B D
4
4
A: 0 D: 5
A 13 1
B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
4
4 A: 0 D: 5
A 13 1 B: 3 E: 6
3
2 C: 2 25 / 52
E
C 5
2
B D
A 1 3
2
C E
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms 111
Figure 4.9 A complete run of Dijkstra’s algorithm, with node A as the starting
point. Also shown are the associated dist values and the final shortest-path tree.
2
B D
4
4 A: 0 D:
∞
A 13 1 B: 4 E:
∞
3 C: 2
2
E
C 5
2
B D
4
4
1 3 A: 0 D: 6
A 1 B: 3 E: 7
3
2 C: 2
E
C 5
2
B D
4
Ví dụ: Bước 4 4
A: 0 D: 5
A 13 1
B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
4
4 A: 0 D: 5
A 13 1 B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
A 1 3
2 26 / 52
C E
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
Chapter 4 Algorithms 111
Figure 4.9 A complete run of Dijkstra’s algorithm, with node A as the starting
point. Also shown are the associated dist values and the final shortest-path tree.
2
B D
4
4 A: 0 D:
∞
A 13 1 B: 4 E:
∞
3 C: 2
2
E
C 5
2
B D
4
4
1 3 A: 0 D: 6
A 1 B: 3 E: 7
3
2 C: 2
E
C 5
2
B D
4
4
A: 0 D: 5
A 13 1
B: 3 E: 6
3
2 C: 2
E
C 5
2
B D
4
Ví dụ: Mảng4 prev A: 0 D: 5
A 13 1 B: 3 E: 6
3
2 C: 2
E
C 5
2
B D u prev[u]
A nil
BC
A 1 3 CA
2 DB
C E EB
27 / 52
Nội dung
Khoảng cách và tìm kiếm theo chiều rộng
Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG
Cài đặt hàng đợi ưu tiên dùng mảng
▶ Dùng mảng lưu trữ giá trị khóa cho mỗi phần tử (đỉnh của đồ
thị).
▶ Phép toán insert và decreasekey chạy trong O(1).
▶ nhưng deletemin chạy trong O(|V|)!
▶ Với cách cài đặt này, thuật toán Dijkstra chạy trong O(|V|2)
29 / 52
Dùng Binary Heap
▶ Các phần tử được lưu trong cây nhị phân đầy đủ: Mỗi mức
trên cây phải được điền đầy từ trái qua phải và phải đầy trước
khi thêm mức tiếp theo.
▶ Ràng buộc: Giá trị khóa của nút trên cây phải nhỏ hơn hoặc
bằng giá trị khóa của các con.
▶ Các phép toán insert, decreasekey, và deletemin chạy
trong O(log |V|)
30 / 52
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Ví dụ: ThêmFigure phần 4.11 tử với(a) khóa A binary7 vào heap binary with heap 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
31 / 52
10 5 7 5
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5 32 / 52
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 33 / 52 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5 34 / 52
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5
11 7 6 8 11 10 6 8
Ví dụ: Xóa phần tử ở gốc (deletemin)
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
35 / 52
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6 36 / 52
11 10 6 8 11 10 12 8
15 20 13 15 20 13
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
37 / 52
P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO
das23402 Ch04 GTBL020-Dasgupta-v10 August 12, 2006 1:48
116 4.6 Shortest paths in the presence of negative edges
Figure 4.11 (a) A binary heap with 10 elements. Only the key values are
shown. (b)–(d) The intermediate “bubble-up” steps in inserting an element with
key 7. (e)–(g) The “sift-down” steps in a delete-min operation.
(a) 3 (b) 3
10 5 10 5
11 12 6 8 11 12 6 8
15 20 13 15 20 13 7
(c) 3 (d) 3
10 5 7 5
11 7 6 8 11 10 6 8
15 20 13 12 15 20 13 12
(e) (f) 12
7 5 7 5
11 10 6 8 11 10 6 8
15 20 13 12 15 20 13
(g) 5 (h) 5
7 12 7 6
11 10 6 8 11 10 12 8
15 20 13 15 20 13
38 / 52
Nội dung
Khoảng cách và tìm kiếm theo chiều rộng
Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG
Câu hỏi
Liệu ta đã quyết định được đường đi ngắn nhất từ S đến A bằng
bao nhiêu chưa?
A
3
S ?−2
4
B
40 / 52
Giải pháp
u
dist[u]
s l(u, v)
dist[v] v
procedure update((u, v) ∈ E)
dist(v) = min{dist(v), dist(u) + l(u, v)}
Ý tưởng: Khoảng cách từ s tới v không thể lớn hơn khoảng cách
từ s tới u, cộng với l(u, v).
41 / 52
procedure update((u, v) ∈ E)
dist(v) = min{dist(v), dist(u) + l(u, v)}
Câu hỏi
Giả sử
dist(S) = dist(A) = dist(B) = ∞.
Ta cần dùng hàm update() mấy lần thì tìm được khoảng cách
ngắn nhất từ S đến A?
A
3
S −2
4
B
42 / 52
Dãy update để tìm đường đi ngắn nhất
▶ Lấy một đỉnh T bất kỳ và xét đường đi ngắn nhất từ S tới T:
S u1 u2 ··· uk T
▶ Đường đi này có nhiều nhất |V| − 1 đỉnh. Tại sao?
Quan sát
Mọi cách gọi update trên dãy cạnh có chứa dãy con
(S, u1), (u1, u2),..., (uk, T)
đều tính đúng khoảng cách từ S tới T. Tại sao?
43 / 52
Thuật toán Bellman-Ford
procedure shortest-paths(G, l, s)
Input: đồ thị có hướng G = (V, E);
độ dài các cạnh {le : e ∈ E}
mà không có chu trình âm;
đỉnh s ∈ V
Output: Với mỗi đỉnh u đến được từ s,
dist(u) = khoảng cách từ s tới u.
for all u ∈ V:
dist(u) = ∞
prev(u) = nil (chưa sử dụng)
dist(s) = 0
repeat |V| − 1 times:
for all edges e ∈ E:
update(e)
44 / 52
P1: OSO/OVYP1: OSO/OVY P2: OSO/OVY P2: OSO/OVY QC: OSO/OVYQC: OSO/OVY T1: OSO T1: OSO
das23402das23402Ch04Ch04 GTBL020-Dasgupta-v10 GTBL020-Dasgupta-v10 AugustAugust 12, 200612, 2006 1:48 1:48
118 118 4.64.6 Shortest Shortest paths paths in the in presence the presence of negative of negative edges edges
FigureFigure 4.13 4.13TheThe Bellman-Ford Bellman-Ford algorithm algorithm for forsingle-source single-source shortest shortest paths paths in in
generalgeneral graphs. graphs.
procedureprocedure shortest-paths shortest-paths(G,(lG, s,)l, s)
Input:Input: Directed Directed graph graphG G(V,(EV),;E );
= =
edgeedge lengths lengthsle : e E withwith no no negative negative cycles; cycles;
{ le∈: e } E
vertexvertexs sV V { ∈ }
∈
Output:ForOutput:For all all vertices vertices∈ u reachableu reachable from froms,s dist(, dist(u)u is) is set set
toto the the distance distance from froms tos tou. u.
forfor all allu uV: V:
∈
distdist(u) (u)∈
= ∞
prevprev(u) (u)nil= ∞nil
= =
distdist(s) (s)0 0
=
repeatrepeatV =V1 times:1 times:
| | −
forfor all all| e| −eE : E :
∈
update(update(e) ∈e)
FigureFigure 4.14 4.14TheThe Bellman-Ford Bellman-Ford algorithm algorithm illustrated illustrated on aon sample a sample graph. graph.
Ví dụ
10 10
S S A A
8 8 1 1 IterationIteration
NodeNode 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7
B B S S 0000000000000000
G G 4 4
− − A A 1010 10 10 5 5 5 5 5 5 5 5 5 5
∞ ∞
B B 1010 6 6 5 5 5 5 5 5
1 1 2 2 1 1 ∞∞∞∞∞∞
C C 1111 7 7 6 6 6 6
∞∞∞∞∞∞∞∞
D D 1414 10 10 9 9
∞∞∞∞∞∞∞∞∞∞
F F 2 2 C C E E 1212 8 8 7 7 7 7 7 7 7 7
− − ∞∞∞∞
F F 999999999999
1 1 3 3 ∞∞∞∞
− − G G 88888888888888
∞ ∞
E E 1 1D D
− −
A noteA note about about implementation: implementation: for formany many graphs, graphs, the the maximum maximum number number of edges of edges
in anyin any shortest shortest path path is substantially is substantially less less than thanV V1, with1, with the the result result that that fewer fewer
| | −
roundsrounds of updates of updates are areneeded. needed. Therefore, Therefore, it makes it| makes| − sense sense to add to add an extraan extra check check to to
the shortest-path algorithm,the shortest-path to make algorithm,it terminate to immediately make it terminate after any immediately round in after any round in
whichwhich no update no update occurred. occurred. 45 / 52
4.6.24.6.2 Negative Negative cycles cycles
If theIf thelength length of edge of edge (E , (BE), inB) Figure in Figure 4.14 4.14 were were changed changed to to4, the4, the graph graph would would
−
havehave a negative a negative cycle cycle A AE E B B A. InA. such In such situations, situations, it− doesn’t it doesn’t make make sense sense
→ →→ →→ →
Câu hỏi
Làm thế nào để tìm được đường đi ngắn nhất theo thuật toán
Bellman-Ford?
46 / 52
Kiểm tra sự tồn tại của chu trình độ dài âm?
▶ Bài toán đường đi ngắn nhất từ s đến t sẽ không có ý nghĩa
nếu từ s đến t có thể đi qua chu trình độ dài âm.
▶ Trong thuật toán Bellman-Ford, thay vì dừng sau |V|−1 vòng
lặp, ta thực hiện thêm một lần nữa.
▶ Đồ thị có chu trình độ dài âm nếu và chỉ nếu tồn tại đỉnh v
mà dist[v] vẫn bị giảm sau vòng cuối.
47 / 52
Nội dung
Khoảng cách và tìm kiếm theo chiều rộng
Thuật toán Dijkstra
Cài đặt hàng đợi ưu tiên
Đường đi ngắn nhất khi có cạnh độ dài âm
Đường đi ngắn nhất trong một DAG
Thuật toán Bellman-Ford cho DAG
2
3 −1 −2
S A B C
−2
Trong DAG, cần update những cạnh nào?
49 / 52
2
3 −1 −2
S A B C
−2
Tính chất
Với mọi đường đi của DAG, các đỉnh xuất hiện theo thứ tự topo.
50 / 52
procedure dag-shortest-paths(G, l, s)
Input: DAG G = (V, E);
độ dài các cạnh {le : e ∈ E}; đỉnh s ∈ V
Output: Với mỗi đỉnh u đến được từ s, dist(u) được
đặt bằng
khoảng cách từ s tới u.
for all u ∈ V:
dist(u) = ∞
prev(u) = nil
dist(s) = 0
Sắp topo các đỉnh của G
for each u ∈ V, theo thứ tự topo:
for all edges (u, v) ∈ E:
update(u, v)
51 / 52
2
3 −1 −2
S A B C
−2
Bài tập
Hãy liệt kê các lệnh update theo thuật toán Bellman-Ford cho
DAG?
52 / 52File đính kèm:
 bai_giang_toan_roi_rac_chuong_duong_di_tren_do_thi_version_0.pdf
bai_giang_toan_roi_rac_chuong_duong_di_tren_do_thi_version_0.pdf

