FPGA implementation of high-Performance DOA estimation using a uniform circular array

, M – 1, have the 
frequency and phase which are translated with a frequency and phase shift equal to the 
frequency and initial phase of DDS, therefore, the phase differences between input 
signals incoming from pairs of antenna elements equal to that of the respective output 
signals of DDCs, and 
 u n a  s n n n (20) 
 T M 1
 u n u0 n u 1 n ... uM 1 n (21) 
     T M 1
 n n n0 n n 1 n ... nM 1 n (22) 
where n n is the noise vector filtered at the outputs of DDCs; s n presents a 
modified version of the signal s(n) shifted frequency and phase equal to the frequency and 
initial phase of DDS; s(n) is the discretized signal of s(t) in (9). 
 We assume that noises ni n are uncorrelated and they are uncorrelated with the 
sourced signals ui(n), i = 0, 1, , M – 1. Let us consider the cross-correlation between 
two consecutive signals at the outputs of DDCs. 
 yi n u i n u( i 1) mod M n 
 (23) 
 s n s  n ai  a(1)mod i M  n  i n n  (1)mod i M n 
 Because the power of filtered noises at the outputs of DDCs is very small, (23) 
can be written as: 
 yi n s i n s  n a i  a( i 1)mod M  (24) 
 From (2) we have 
 4 R 2 i 
 a  a(i 1) mod M  exp j sin sin  (25) 
 i  MMM 
 The cross-correlation signals yi(n) are obtained by using the complex multipliers 
in FPGA. The phase of signals yi(n) can be estimated based on CORDIC Artan 
(COordinate Rotation DIgital Computer) algorithm [16]. 
 4 R 2 i 
 i sin sin  (26) 
  MMM 
68 
 Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
 DOA values θ can be obtained by using trigonometric operators and CORDIC 
Artan function. In this paper, DOA estimation algorithm is given for M = {3, 4, 5}. For 
other values of M, DOA estimation algorithm can be obtained similarly. 
 For M = 3 
 3
  arctan 2 (27) 
 1  0
 For M = 4 
  
  arctan 0 1 (28) 
 3  2
 For M = 5 
 4 2 
 2 sin sin 
 3 5 5 2
  arctan (29) 
 5 4  3  0  1 
4. Experimental results 
 In this paper, the performance of the proposed hardware scheme of DOA estimation 
receiver is evaluated. System Generator for DSP tool is selected in the design, because it 
is a system-level modeling tool from Xilinx that enables the use of the MathWorks 
model-based Simulink design environment for FPGA design. System Generator for DSP 
tool is a flexible high-level system modeling environment. In a System Generator design, 
signals are not just bits. They can be signed and unsigned fixed-point numbers, and 
changes to the design automatically translate into appropriate changes in signal types. 
That is generally preferred for DSP applications which often require fixed-point 
arithmetic operations. Simulations in System Generator are considerably faster than those 
from the traditional HDL simulators, and results are easier to analyze. 
 Assume that the RF/IF input of DOA estimation system includes noises and signal 
carriers of 20.05, 43.92 and 70.05 MHz. The signal with frequency carrier of 43.92 MHz is 
the strongest (Fig. 6) and arrives at the center of UCA with directions of arrival of π/4. The 
sampling frequency of ADC is 200 MHz. The number of antenna elements in UCA is 5. 
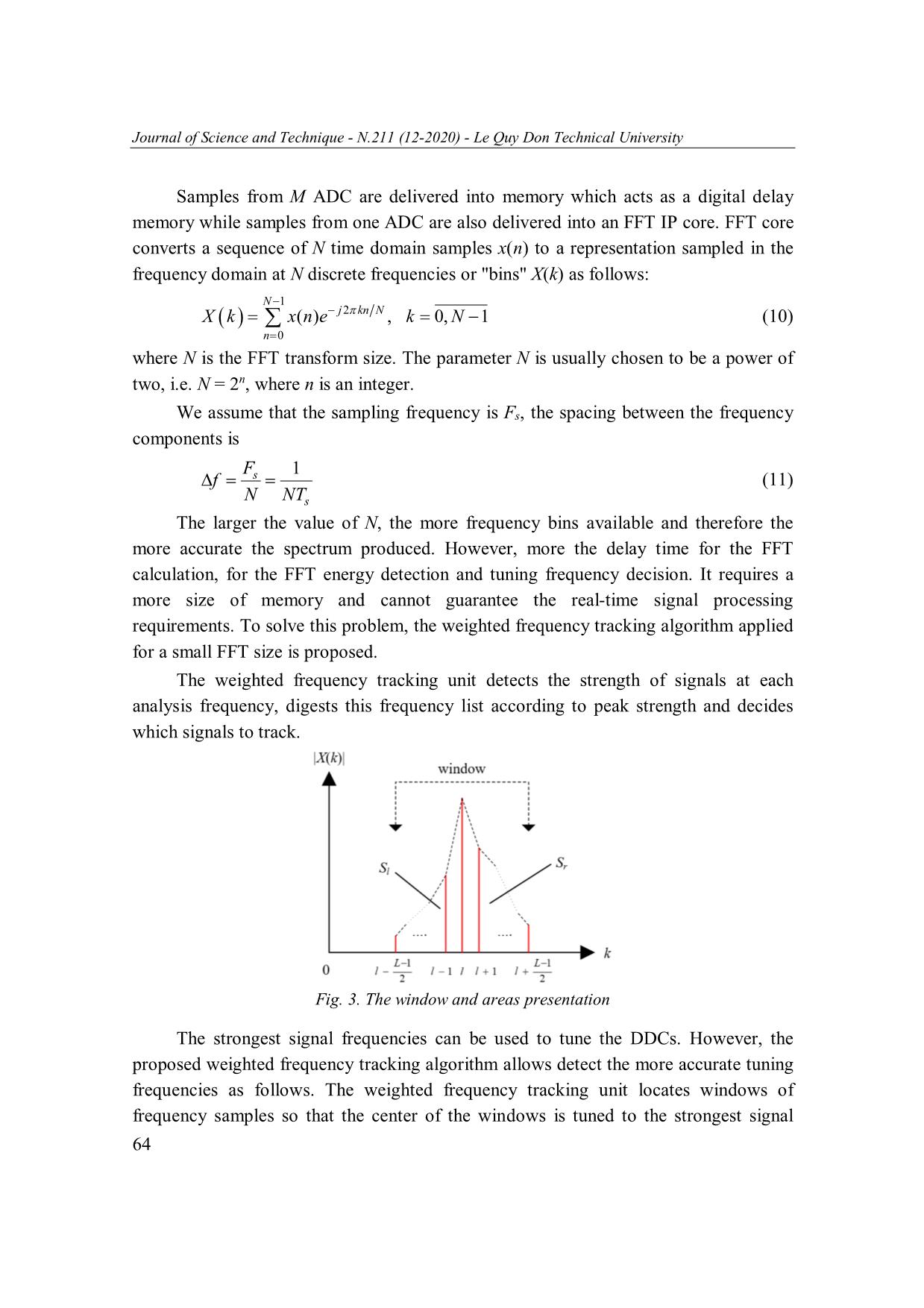
 Fig. 6. Spectrum of incoming signals and noises 
 69
Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
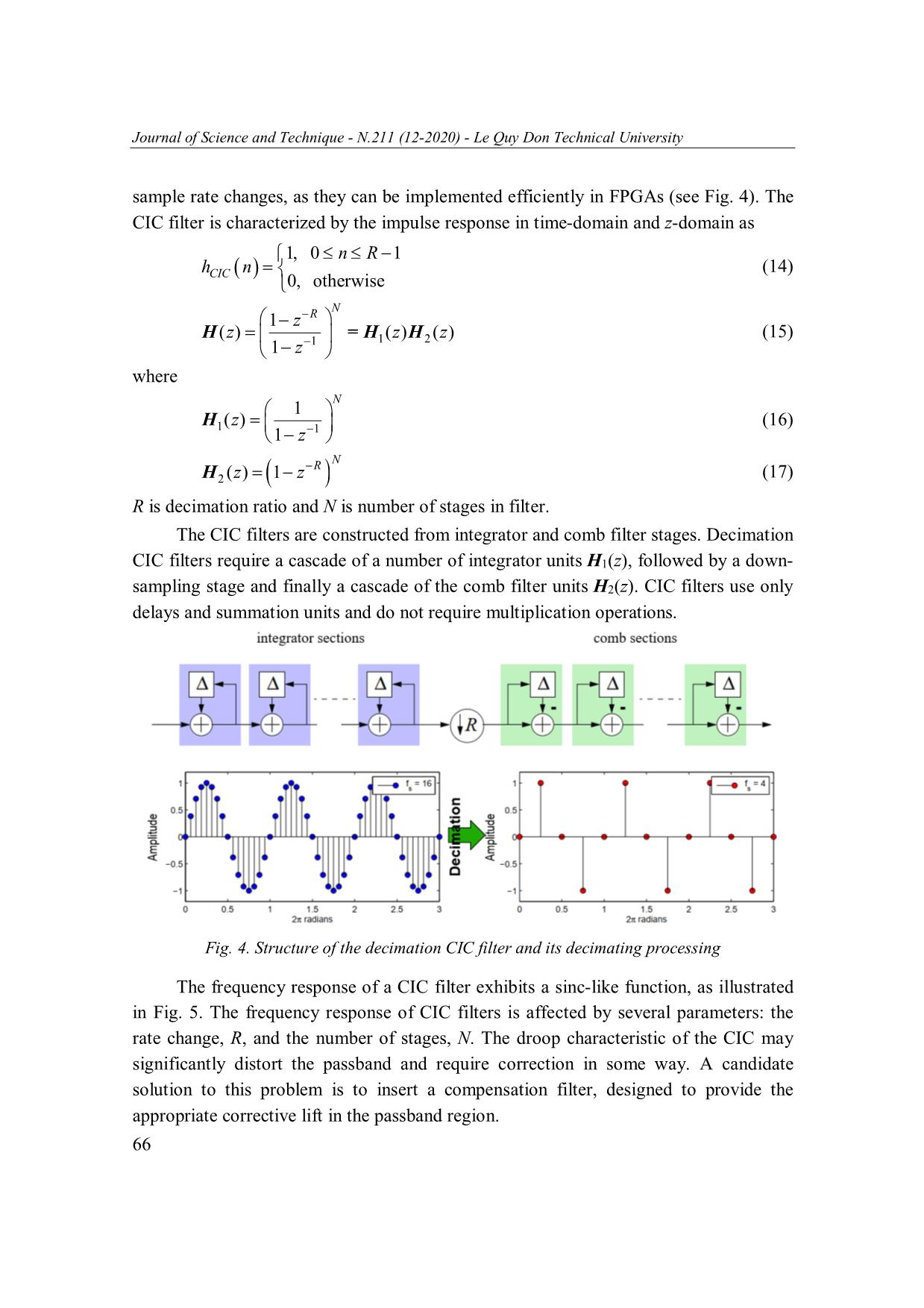
 Received results from the System Generator for DSP tool in Fig. 7 show that 
4096-point FFT gives three peaks, the weighted frequency tracking unit locks onto the 
analysis frequency index of 899 and calculates the ltune value (about 899.4). Hence, value 
of fdds = 200e6/4096ltune ≈ 43.916 MHz. If the weighted frequency tracking unit is not 
used, ltune will lock onto value of 899. In this case, fdds = 899×200e6/4096 = 43.896 MHz. 
Therefore, the frequency of DDS is more accuracy calculated, when the weighted 
frequency tracking unit is used. Also, from Fig. 7, DOA estimation value is about 
0.7854 ≈ π/4 radian. 
 (a) 
 (b) 
 (c) 
 Fig. 7. Received results on System Generator for DSP tool: (a) Strength of the frequency 
 components on the FFT output; (b) Signal generated by the DDS; (c) DOA estimation result. 
70 
 Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
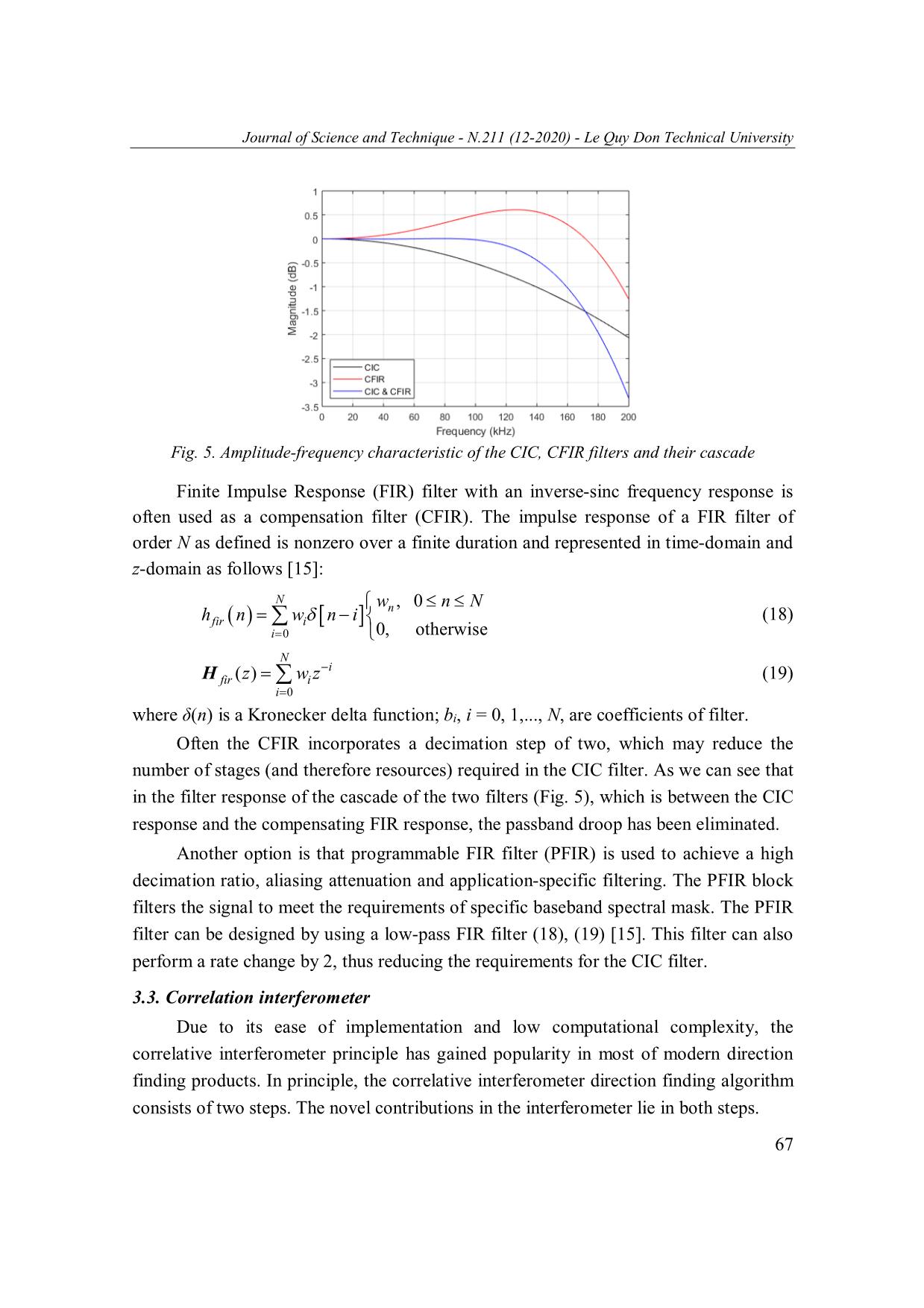
 The proposed hardware architecture of the DOA estimation receiver described in 
this paper has been implemented and tested on Xilinx FPGA chip using the ML507 board 
and ADC board (see Fig. 8). The ADC board includes six 10-bit ADCs AD9211-250 
which operates up to 250 MSPS conversion rate. To indicate experimental results, the 
ML507 board is connected to a computer and VGA/LCD display. The DOA estimation 
values are transmitted to the computer via a simple serial interface RS-232. These DOA 
estimation values are also presented on VGA/LCD screen. The experimental signal is 
generated in a frequency hopping transmitter located at different directions. The 
transmitting radio signals of this transmitter change in available frequency band of 
5-100 MHz. The clock frequency of FPGA Fclk and conversion rate of ADCs Fs is 
234 MHz. This clock frequency is selected to work with standard monitors at the 
1920x1440@60Hz VGA mode. The number of ADCs connected to FPGA is 4 
(therefore, the number of antenna elements is M = 4) and only six MSB bits of these 
ADCs are used. This is because the number of FPGA I/Os (input/output pins) on the 
expansion header of ML507 board is 32. 
 Fig. 8. Experimental setup of the proposed DOA estimation receiver 
 The 4096-point FFT is used in experiments. From equation (11) the spacing 
between the frequency components X(k) is Δf = Fs/NFFT = 234/4096 ≈ 57.129 kHz. 
Maximum carrier frequency of the experimental transmitting signal is fmax = 100 MHz. 
Therefore, the maximum frequency component X(k) on the FFT output approximated to 
fmax has index kmax = fmax/Δf = 1750. 1751 amplitude values of X(k), k = 0, 1,..., kmax, are 
displayed on the center of the screen corresponding to 1751 of 1920 pixels (see Fig. 9). 
 71
Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
 (a) (b) 
 Fig. 9. Display results on VGA/LCD monitor: (a) when three signal frequencies are observed 
 on the screen; (b) when two signal frequencies are observed on the screen. 
 From Fig. 9 can see that the signal frequency is hopped. One observation can see 
2-3 carriers. The DOA values are estimated and displayed at locations corresponding to 
each carrier frequency. They are similar with angle values about 90 degrees, because the 
position of the transmitter is unchanged. These DOA values are also transmitted to PC 
and presented on the indicator (green line in Fig. 10). Fig. 10 shows that the indication 
lines (green line) are located at the angle of 90 degrees. 
 Experimental results at the angle of 45 degrees are shown in Fig. 11. When the 
transmitter changes carriers with a small frequency value, the proposed DOA estimation 
receiver has ability to track them and estimates truly DOA. This can be seen in Fig. 11a. 
Two of three carriers have frequency values which vary a small amount. Their estimated 
DOAs are similar and have value of 45 degrees. The indication lines on computer are 
indicated at the corresponding angle (45 degrees). 
 Fig. 10. DOA indicator at 90 degrees on computer. 
72 
 Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
 (a) (b) 
 Fig. 11. Experimental results at the angle of 45 degrees: 
 (a) on VGA/LCD monitor; (b) on PC indicator. 
 In the expriments, at the each position of the transmitter, the transmitting radio 
signals are changed with the frequency hop step of 100 kHz. The experimental 
parameters and results of these trials are shown in Tab. 1. The proposed receiver 
estimates independently the signal frequency and its DOA, so the received estimation 
results of the frequency and DOA are independent of each other. The mean values of 
DOA estimates were calculated on 10 hopped frequencies. While the mean values of 
frequency estimates were calculated on 10 positions of the transmitter. The FPGA 
resource utilisation of the proposed hardware architecture is summarised in Tab. 2. 
 Tab. 1. The experimental parameters and measurement results 
 Parameters Values 
Signal frequency (kHz) 5200 12500 14900 16500 47600 54000 65000 72300 80600 97100 
Estimated frequency 
 5196 12505 14904 16503 47595 53907 65008 72301 80608 97102 
(kHz) 
Signal DOA (degrees) 0 30 45 60 90 120 150 180 240 270 
Estimated DOA 
 0.1 30.3 45.1 59.2 89.5 119.7 150.2 179.6 239.3 269.6 
(degrees) 
 Tab. 2. FPGA resource utilisation of the proposed hardware architecture 
 Device resources Available Used Utilisation 
 Slice look-up-tables (LUTs) 44,800 9,874 22% 
 Slice registers 44,800 11,150 24% 
 Block RAM tile 148 20 13% 
 DSP48E 128 116 91% 
 Maximum frequency (MHz) 318.288 
 Output latency (clock cycles) 4208 
 73
Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
 From Tab. 1 can see that the estimated DOA results are close to the actual angles 
(the DOA estimation accuracy is smaller than 1 degree). The frequency estimation 
accuracy is below 10 kHz for the transmitting frequency band of 5-100 MHz. The 
frequency and DOA estimation accuracy is suitable for electronic attack systems, in 
which noise jammers place a signal into the receiver to interfere with the reception or 
processing of the desired signal [17]. 
 The processing delay is 4208 clock cycles (approximates to the FFT size, see Tab. 2), 
i.e. it is equal to 4208*Tclk ≈ 16 μs. While existing fast frequency hopping systems can 
achieve up to 5000 hops, but not faster, because a synchronization is required between 
the transmitter node and the receiver node. The existing time of each frequency of the 
transmitting signal is 0.2 ms. Therefore, the processing delay of the proposed hardware 
architecture can guarantee that the noise jammer attacks the receiver within the existing 
duration of the signal. 
 Compared to the hardware architectures proposed in [4, 7], the hardware 
architecture in this paper requires a very small FPGA resource utilisation. This is 
because, the proposed architecture uses a small number of antennas (hence, it uses a few 
number of DDCs blocks in compared to [4]) and does not use the matrix operations. 
Moreover, the frequency tracker used in the proposed architecture tunes the center 
frequency of the DDCs that makes it suitable to estimate the DOA of frequency hopping 
communication systems. This feature is not obtained in [4, 7]. 
5. Conclusions 
 In this paper, the author has proposed the DOA estimation receiver including 
frequency tracker, DDCs and correlation interferometer, and implemented it on FPGA. 
The proposed hardware architecture has a low complexity and more suitable for DOA 
estimation of frequency hopping communication systems. The simulation results of the 
proposed signal processing hardware architecture on the System Generator for DSP 
Tool and its FPGA implementation show that the proposed receiver has the ability to 
lock, track and estimate the frequency hopping signals. 
References 
1. A. G. Raj and J. H. McClellan (Jan. 2019). Single Snapshot Super-Resolution DOA Estimation 
 for Arbitrary Array Geometries. IEEE Signal Processing Letters, 26(1), pp. 119-123. 
2. M. Esfandiari, S. A. Vorobyov, S. Alibani and M. Karimi (Jun. 2019). Non-Iterative 
 Subspace-Based DOA Estimation in the Presence of Nonuniform Noise. IEEE Signal 
 Processing Letters, 26(6), pp. 848-852. 
3. P. Vallet, X. Mestre and P. Loubaton (Dec. 2015). Performance Analysis of an Improved 
 MUSIC DoA Estimator. IEEE Transactions on Signal Processing, 63(23), pp. 6407-6422. 
4. Y. Xie, C. Peng, X. Jiang and S. Ouyang (2014). Hardware design and implementation of DOA 
 estimation algorithms for spherical array antennas. 2014 IEEE ICSPCC, Guilin, pp. 219-223. 
74 
 Journal of Science and Technique - N.211 (12-2020) - Le Quy Don Technical University 
5. A. Liu, X. Zhang, Q. Yang, X. Wu and W. Deng (2019). Combined root-MUSIC 
 algorithms for multi-carrier MIMO radar with sparse uniform linear arrays. IET Radar, 
 Sonar Navigation, 13(1), pp. 89-97. 
6. A. Herzog and E. A. P. Habets (Apr. 2019). Eigenbeam-ESPRIT for DOA-Vector 
 Estimation. IEEE Signal Processing Letters, 26(4), pp. 572-576. 
7. A. A. Hussain, N. Tayem, M. O. Butt, A. Soliman, A. Alhamed and S. Alshebeili (2018). 
 FPGA Hardware Implementation of DOA Estimation Algorithm Employing LU 
 Decomposition. in IEEE Access, 6, pp. 17666-17680. 
8. Z. Yang, P. Stoica and J. Tang (May 2019). Source Resolvability of Spatial-Smoothing-
 Based Subspace Methods: A Hadamard Product Perspective. IEEE Transactions on Signal 
 Processing, 67(10), pp. 2543-2553. 
9. R. P. Lemos, H. V. L. e. Silva, E. L. Flores, J. A. Kunzler and D. F. Burgos (Dec. 2016). 
 Spatial Filtering Based on Differential Spectrum for Improving ML DOA Estimation 
 Performance. IEEE Signal Processing Letters, 23(12), pp. 1811-1815. 
10. B. Yao, W. Zhang and Q. Wu (2017). Weighted Subspace Fitting for Two-Dimension DOA 
 Estimation in Massive MIMO Systems. IEEE Access, 5, pp. 14020-14027. 
11. T. Cheng, X. Gui and X. Zhang (Feb. 2013). A dimension separation-based two-
 dimensional correlation interferometer algorithm. EURASIP Journal on Wireless 
 Communications and Networking, 2013(1). 
12. D. Torrieri (2018). Principles of Spread-Spectrum Communication Systems, 4th edition. 
 Springer International Publishing AG, part of Springer Nature. 
13. Xilinx, “PG141: DDS Compiler v6.0, LogiCORE IP Product Guide” Dec. 2017. 
14. Xilinx, “PG140: CIC Compiler v4.0, LogiCORE IP Product Guide” Oct. 2016. 
15. Xilinx, “PG149: FIR Compiler v7.2, LogiCORE IP Product Guide” June 2020. 
16. Xilinx, “PG105: CORDIC v6.0, LogiCORE IP Product Guide” Dec. 2017. 
17. James Genova, “Electronic Warfare Signal Processing” Artech House, Boston, London, 2018. 
THỰC THI ƯỚC LƯỢNG GÓC HƯỚNG HIỆU SUẤT CAO SỬ DỤNG 
 MẢNG ĂNG TEN TRÒN ĐỒNG NHẤT TRÊN FPGA 
 Tóm tắt: Trong bài báo này, tác giả trình bày kiến trúc phần cứng xử lý tín hiệu để khóa 
tần số tín hiệu quan tâm có ở đầu vào, bám chúng nếu tần số thay đổi và ước lượng góc hướng 
đến (DOA) của tín hiệu quan tâm bằng cách sử dụng mảng ăng ten tròn đồng nhất. Kiến trúc 
phần cứng đề xuất được mô tả chi tiết, được thực thi và kiểm chứng bằng các thử nghiệm thực 
tế trên chip FPGA. Các kết quả thử nghiệm cho thấy rằng độ chính xác ước lượng DOA nhỏ 
hơn 1 độ. Độ chính xác ước lượng DOA này phù hợp với các hệ thống tấn công điện tử. 
 Từ khóa: Góc hướng đến; bộ đảo tần xuống số; bộ bám tần số; bộ so pha tương quan; 
mảng ăng ten tròn đồng nhất. 
 Received: 02/7/2020; Revised: 18/11/2020; Accepted for publication: 26/11/2020 
  
 75