Entangled state generation in a linear coupling coupler
The nonlinear coupler, which consists of two nonlinear oscillators
linearly coupled together and one or two of these oscillators excited by external
coherent fields, is investigated. We show that evolution of the nonlinear coupler is
possible closed in a finite set of n-photon Fock states and can create Bell-like states.
Especially, the entropy of entanglement and the Bell-like states vary dramatically with
the different initial conditions are discussed. These results are compared with that
obtained previously in the literature.

Trang 1

Trang 2

Trang 3

Trang 4
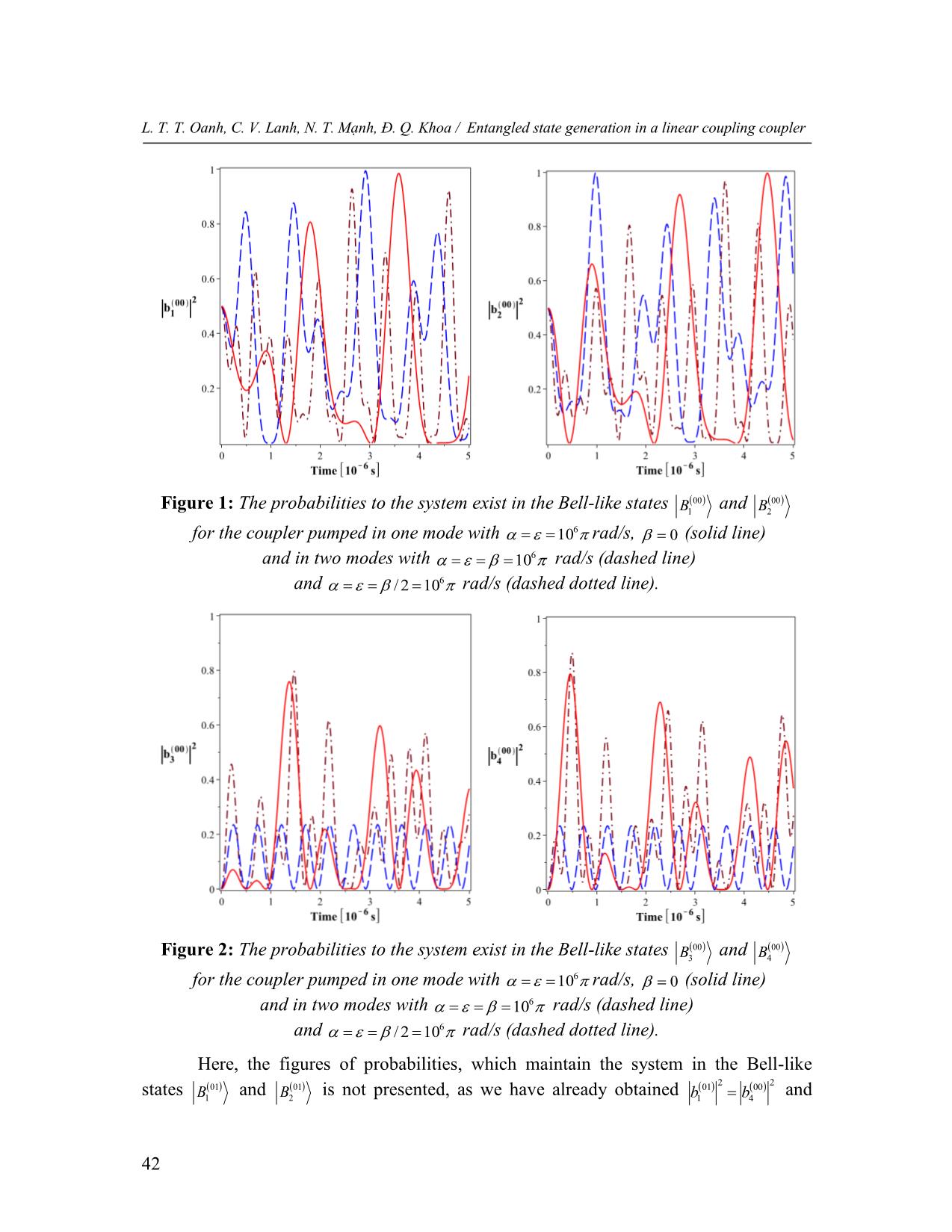
Trang 5
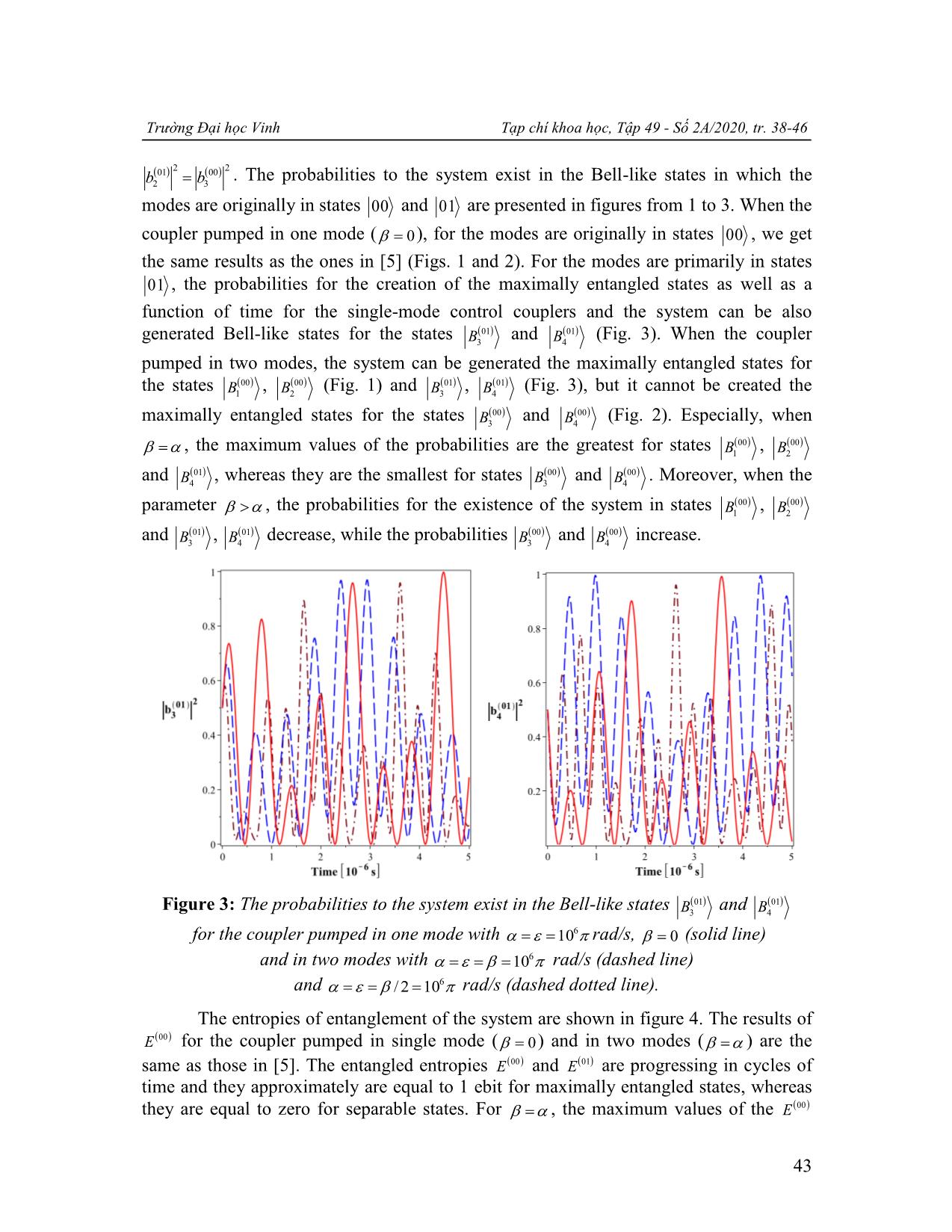
Trang 6
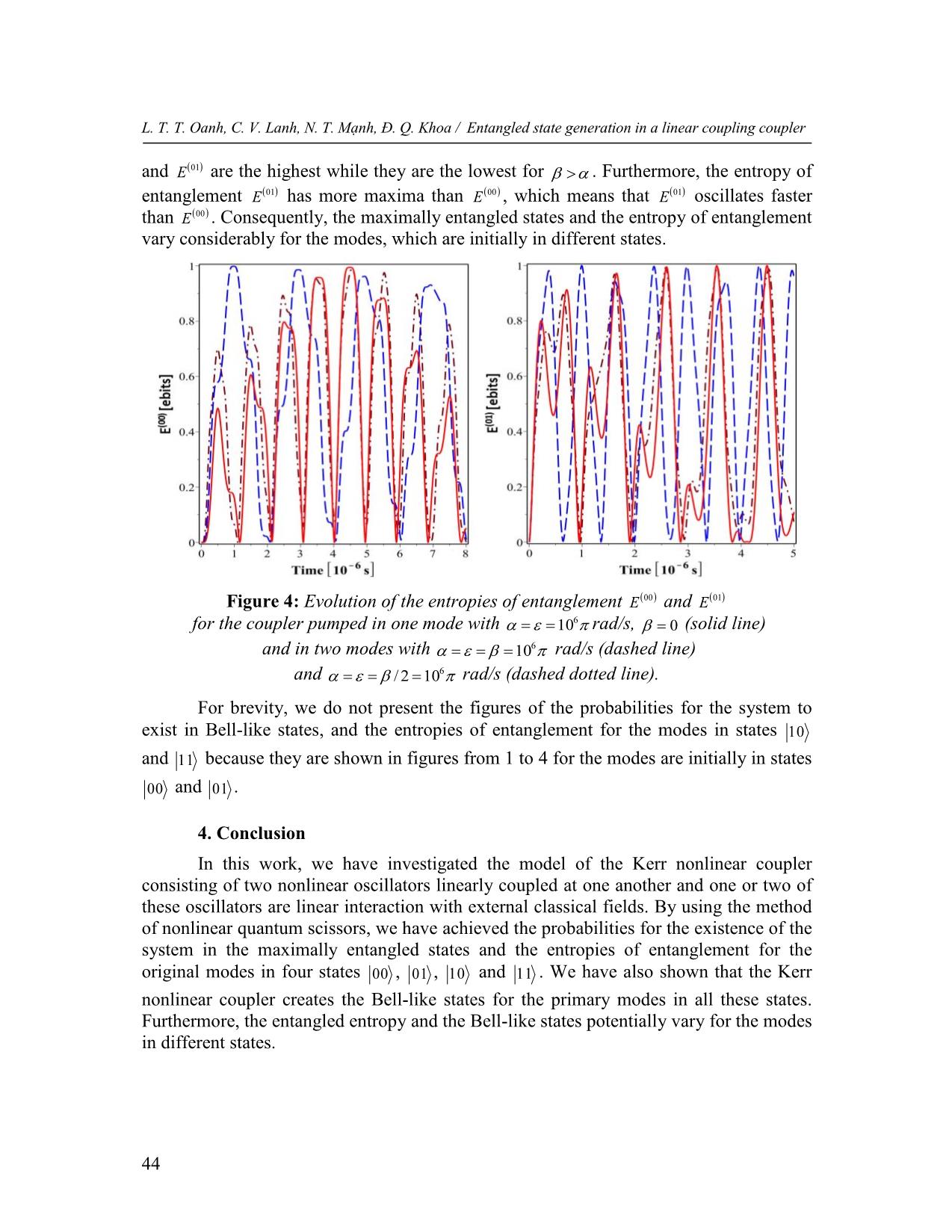
Trang 7

Trang 8

Trang 9
Bạn đang xem tài liệu "Entangled state generation in a linear coupling coupler", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Entangled state generation in a linear coupling coupler

ators excited by external coherent fields, is investigated. We show that evolution of the nonlinear coupler is possible closed in a finite set of n-photon Fock states and can create Bell-like states. Especially, the entropy of entanglement and the Bell-like states vary dramatically with the different initial conditions are discussed. These results are compared with that obtained previously in the literature. Keywords: Kerr nonlinear coupler; Bell-like state; entropy of entanglement. 1. Introduction Scientists are interested in two-mode nonlinear couplers, which are introduced by Jensen [1] because of their wide applicability. The nonlinear optical couplers, which rely on Kerr effect, have drawn exceptional care about both classical [1] and quantum [2] systems. The Kerr nonlinear couplers can display changes of effects as self-switching and self-trapping. For quantum fields, they are able to also create squeezed light and sub- Poissonian [3]. It is also researched on the probabilities of creating entangled states in Kerr nonlinear couplers [4]. Kerr nonlinear couplers involve two nonlinear oscillators interacting linear [5] and nonlinear [6] together. The models are advance in couplers with three nonlinear oscillators [7], the three-qubit models in phenomena of quantum steering [8], the model of three interacting qubits [9]. In this paper, we investigate Kerr nonlinear couplers including two quantum nonlinear oscillators linearly coupled together in which one or two of these oscillators excited by external classical fields and extend the consideration for all initial conditions of the motion equations of complex probability amplitudes. We show that the Bell-like states can be created in the Kerr nonlinear couplers under suitable conditions. We also compare the abilities to create Bell-like states by the nonlinear couplers pumped in one and two modes for different initial conditions of the motion equations. 2. The Kerr nonlinear coupler 2.1. The Kerr nonlinear coupler pumped in one mode Email: khoa_dqspqt@yahoo.com (Đ. Q. Khoa) 38 Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 2A/2020, tr. 38-46 The Kerr nonlinear coupler, which involves two nonlinear oscillators linearly interacted together, and one of these oscillators linearly interacts to an external coherent field, is studied. Therefore, the system might be depicted by the Hamiltonian [10] with the form as 2 ˆ ˆ ˆ a 2 2 b ˆ ˆ2 ˆ * ˆ * H aaˆ aˆ bb b aˆ aˆ b b aˆ b aˆb aˆ aˆ , (1) 2 2 here aˆ bˆ and abˆ ˆ are bosonic creation and annihilation operators, corresponding to the a (b) mode of the nonlinear oscillators, respectively; a ( b ) is Kerr nonlinearity of the mode a (b); the parameters and are the external coherent field for the mode a and the oscillator-oscillator coupling strength, respectively. The evolution of our system without damping processes can be represented in the n-photon Fock basis states with the following form , (2) (t) cmn (t) mn m,n 0 in which cmn (t) are the complex probability amplitudes of the system. By using the formalism of the nonlinear quantum scissors discussed in [5], we show that the time-dependent wave function of our system can be truncated into the simple form as (t) c ij (t) 00 c ij (t) 01 c ij (t) 10 c ij (t) 11 cut 00 01 10 11 , (3) i, j 0,1 are the sign of oscillator modes, which are initially in states ij . Using the Schrödinger equation, the motion equations of the complex probability amplitudes can be depicted by the equations as d i c ij (t) *c ij (t), dt 00 10 d i c ij (t) *c ij (t) *c ij (t), dt 01 10 11 d (4) i c ij (t) c ij (t) c ij (t), dt 10 01 00 d i c ij (t) c ij (t). dt 11 01 By supposing that and are real and for the time t = 0, both modes are originally in vacuum states ( (t 0) 00 ), then the solutions of Eqs. (4) grow into exactly the same cut as those in [5]: 39 L. T. T. Oanh, C. V. Lanh, N. T. Mạnh, Đ. Q. Khoa / Entangled state generation in a linear coupling coupler 00 1 1t 2t c00 (t) cos cos , 2 2 2 00 1t 2t c01 (t) cos cos , 2 2 (5) 00 i 2 1t 2t c10 (t) sin sin , 4 2 2 00 i 1t 2t c11 (t) 2 sin 1 sin . 2 2 2 On the other hand, by assuming that for the time t = 0, one mode is originally in vacuum state and other mode is in single-photon Fock state ( (t 0) 01 ), we get the solutions cut ij of Eqs. (4) for cmn , m,n 0,1 in the form as 01 00 c00 (t) c01 (t), 01 1 1t 2t c01 (t) cos cos , 2 2 2 (6) 01 i 1t 2t c10 (t) 2 sin 1 sin , 2 2 2 01 00 c11 (t) c10 (t), 2 2 2 2 2 2 where 1 2[2 ] , 2 2[2 ] , 4 . We now examine the evolution of our system for the cases when the modes are primarily in states 10 and 11 . Therefore, the evolution of the system for these initial states has the form as 10 t c 00 00 c 01 01 c 01 10 c 00 11 , (7) cut 10 10 01 01 and 11 t c 00 00 c 00 01 c 00 10 c 00 11 , (8) cut 11 10 01 00 and the entropies of entanglement are also easily obtained as E 11 t E 00 t , E 10 t E 01 t . (9) 2.2. The Kerr nonlinear coupler pumped in two modes The Kerr nonlinear coupler pumped in two modes is similar to the coupler pumped in single mode, except both modes of this coupler are coupled by external coherent fields. Hence, the Hamiltonian depicting such system has the following form 2 2 Hˆ a aˆ aˆ 2 b bˆ bˆ2 aˆ bˆ *aˆbˆ aˆ *aˆ bˆ *bˆ . (10) 2 2 40 Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 2A/2020, tr. 38-46 This Hamiltonian is similar to the one defined by (1), except for the term bˆ *bˆ , in which is the coupling strength of the mode b with an external coherent field. In this case, we also use the Schrödinger equation and obtain the motion equations of the complex probability amplitudes in the form d i c ij (t) *c ij (t) *c ij (t), dt 00 10 01 d i c ij (t) *c ij (t) *c ij (t) c ij (t), dt 01 10 11 00 (11) d i c ij (t) c ij (t) c ij (t) *c ij (t), dt 10 01 00 11 d i c ij (t) c ij (t) c ij (t). dt 11 01 10 By solving these equations for all initial states of the modes, we shall obtain their solutions similar to those for coupler pumped in single mode. Because of the limitation of the volume in this work scale, we focus only on studying the generation of Bell-like states in the next section, whereas their mathematical details will not be presented. 3. The generation of Bell-like states in the Kerr nonlinear coupler The entropy of entanglement of our system is defined as in [5]: ij E (t) .log2 (1 ).log2 (1 ) , (12) 2 1 1 C ij ij ij ij ij ij where and C 2c00 (t)c11 (t) c01 (t)c10 (t) . 2 The truncation state in (3) can be represented in the Bell basis states in the form: 4 ij ij (t) bl (t) Bl , (13) cut l 1 where Bell states are expanded by the Bell-like states with the form as 1 ij 1 ij B ij 00 i 11 , B ij 11 i 00 , 1 2 2 2 (14) 1 ij 1 ij B ij 01 i 10 , B ij 10 i 01 . 3 2 4 2 ij By using (3) and (13), the coefficients bl can be achieved in the following form 1 1 b ij c ij (t) ic ij (t) , b ij c ij (t) ic ij (t) , 1 2 00 11 2 2 11 00 (15) 1 1 b ij c ij (t) ic ij (t) , b ij c ij (t) ic ij (t) . 3 2 01 10 4 2 10 01 41 L. T. T. Oanh, C. V. Lanh, N. T. Mạnh, Đ. Q. Khoa / Entangled state generation in a linear coupling coupler 00 00 Figure 1: The probabilities to the system exist in the Bell-like states B1 and B2 for the coupler pumped in one mode with 106 rad/s, 0 (solid line) and in two modes with 106 rad/s (dashed line) and /2 106 rad/s (dashed dotted line). 00 00 Figure 2: The probabilities to the system exist in the Bell-like states B3 and B4 for the coupler pumped in one mode with 106 rad/s, 0 (solid line) and in two modes with 106 rad/s (dashed line) and /2 106 rad/s (dashed dotted line). Here, the figures of probabilities, which maintain the system in the Bell-like 01 01 01 2 00 2 states B1 and B2 is not presented, as we have already obtained b1 b4 and 42 Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 2A/2020, tr. 38-46 01 2 00 2 b2 b3 . The probabilities to the system exist in the Bell-like states in which the modes are originally in states 00 and 01 are presented in figures from 1 to 3. When the coupler pumped in one mode ( 0), for the modes are originally in states 00 , we get the same results as the ones in [5] (Figs. 1 and 2). For the modes are primarily in states 01 , the probabilities for the creation of the maximally entangled states as well as a function of time for the single-mode control couplers and the system can be also 01 01 generated Bell-like states for the states B3 and B4 (Fig. 3). When the coupler pumped in two modes, the system can be generated the maximally entangled states for 00 00 01 01 the states B1 , B2 (Fig. 1) and B3 , B4 (Fig. 3), but it cannot be created the 00 00 maximally entangled states for the states B3 and B4 (Fig. 2). Especially, when 00 00 , the maximum values of the probabilities are the greatest for states B1 , B2 01 00 00 and B4 , whereas they are the smallest for states B3 and B4 . Moreover, when the 00 00 parameter , the probabilities for the existence of the system in states B1 , B2 01 01 00 00 and B3 , B4 decrease, while the probabilities B3 and B4 increase. 01 01 Figure 3: The probabilities to the system exist in the Bell-like states B3 and B4 for the coupler pumped in one mode with 106 rad/s, 0 (solid line) and in two modes with 106 rad/s (dashed line) and /2 106 rad/s (dashed dotted line). The entropies of entanglement of the system are shown in figure 4. The results of E 00 for the coupler pumped in single mode ( 0) and in two modes ( ) are the same as those in [5]. The entangled entropies E 00 and E 01 are progressing in cycles of time and they approximately are equal to 1 ebit for maximally entangled states, whereas they are equal to zero for separable states. For , the maximum values of the E 00 43 L. T. T. Oanh, C. V. Lanh, N. T. Mạnh, Đ. Q. Khoa / Entangled state generation in a linear coupling coupler and E 01 are the highest while they are the lowest for . Furthermore, the entropy of entanglement E 01 has more maxima than E 00 , which means that E 01 oscillates faster than E 00 . Consequently, the maximally entangled states and the entropy of entanglement vary considerably for the modes, which are initially in different states. Figure 4: Evolution of the entropies of entanglement E 00 and E 01 for the coupler pumped in one mode with 106 rad/s, 0 (solid line) and in two modes with 106 rad/s (dashed line) and /2 106 rad/s (dashed dotted line). For brevity, we do not present the figures of the probabilities for the system to exist in Bell-like states, and the entropies of entanglement for the modes in states 10 and 11 because they are shown in figures from 1 to 4 for the modes are initially in states 00 and 01 . 4. Conclusion In this work, we have investigated the model of the Kerr nonlinear coupler consisting of two nonlinear oscillators linearly coupled at one another and one or two of these oscillators are linear interaction with external classical fields. By using the method of nonlinear quantum scissors, we have achieved the probabilities for the existence of the system in the maximally entangled states and the entropies of entanglement for the original modes in four states 00 , 01 , 10 and 11 . We have also shown that the Kerr nonlinear coupler creates the Bell-like states for the primary modes in all these states. Furthermore, the entangled entropy and the Bell-like states potentially vary for the modes in different states. 44 Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 2A/2020, tr. 38-46 REFERENCES [1] S. M. Jensen, “The nonlinear coherent coupler”, IEEE Journal of Quantum Electronics, Vol. QE-18, No. 10, pp. 1580-1583, 1982. [2] F. A. A. El-Orany, M. Sebawe Abdalla and J. Peřina, “Quantum properties of the codirectional three-mode Kerr nonlinear coupler”, The European Physical Journal D, Vol. 33, No. 3, pp. 453-463, 2005. [3] A. B. M. A. Ibrahim, B. A. Umarov and M. R. B. Wahiddin, “Squeezing in the Kerr nonlinear coupler via phase-spacerepresentation”, Phys. Rev. A, Vol. 61, No. 4, pp. 043804(1-6), 2000. [4] L. Sanz, R. M. Angelo and K. Furuya, “Entanglement dynamics in a two-mode nonlinear bosonic Hamiltonian”, Journal of Physics A: Mathematical and General, Vol. 36, No. 37, pp. 9737-9754, 2003. [5] A. Miranowicz and W. Leoński, “Two-mode optical state truncation and generation of maximally entangled states in pumped nonlinear couplers”, Journal of Physics B: Atomic Molecular and Optical Physics, Vol. 39, No. 7, pp. 1683-1700, 2006. [6] A. Kowalewska-Kudłaszyk and W. Leoński, “Finite-dimensional states and entanglement generation for a nonlinear coupler”, Physical Review A, Vol. 73, No. 4, pp. 042318(1-8), 2006. [7] J. K. Kalaga, A. Kowalewska-Kudłaszyk, W. Leoński and A. Barasiński, Quantum correlations and entanglement in a model comprised of a short chain of nonlinear oscillators, Physical Review A, Vol. 94, No. 3, pp. 032304(1-12), 2016. [8] J. K. Kalaga and W. Leoński, “Quantum steering borders in three-qubit systems”, Quantum Information Processing, Vol. 16, No. 7, 175(1-23), 2017. [9 J. K. Kalaga, W. Leoński and J. Peřina, Jr., “Einstein-Podolsky-Rosen steering and coherence in the family of entangled three-qubit states”, Physical Review A, Vol. 97, No. 4, pp. 042110(1-12), 2018. [10] W. Leoński and A. Miranowicz, “Kerr nonlinear coupler and entanglement”, Journal of Optics B: Quantum Semiclassical Optics, Vol. 6, No. 3, pp. S37-S42, 2004. 45 L. T. T. Oanh, C. V. Lanh, N. T. Mạnh, Đ. Q. Khoa / Entangled state generation in a linear coupling coupler TÓM TẮT SỰ SINH TRẠNG THÁI ĐAN RỐI TRONG BỘ NỐI LIÊN KẾT TUYẾN TÍNH Bộ nối phi tuyến gồm hai dao động tử phi tuyến liên kết tuyến tính với nhau và một hoặc hai dao động tử này được kích thích bởi các trường kết hợp ngoài được nghiên cứu một cách chi tiết. Chúng tôi chỉ ra rằng sự tiến triển của bộ nối phi tuyến này có thể được đóng trong một tập hợp hữu hạn các trạng thái Fock n-photon và có thể tạo ra các trạng thái kiểu Bell. Đặc biệt, entropy đan rối và các trạng thái kiểu Bell thay đổi một cách đáng kể với các điều kiện đầu khác nhau sẽ được thảo luận. Các kết quả này sẽ được so sánh với những kết quả tìm được trong các công trình trước đó. Từ khóa: Bộ nối phi tuyến Kerr; trạng thái kiểu Bell; entropy đan rối. 46
File đính kèm:
 entangled_state_generation_in_a_linear_coupling_coupler.pdf
entangled_state_generation_in_a_linear_coupling_coupler.pdf

