Điều khiển thiết bị bay loại bốn động cơ sử dụng thuật toán điều khiển tự chỉnh PID mờ
Với những tiến bộ to lớn trong bộ cảm biến thu nhỏ, thiết bị truyền động và bộ vi xử lý tiên tiến,
nhiều nghiên cứu hiện đang tập trung phát triển các loại thiết bị bay nhỏ để sử dụng trong nghiên cứu và
các ứng dụng thương mại. Các dạng mô hình toán học chi tiết cho thiết bị bay điều khiển từ xa, hay loại
không người lái Unmanned Aerial Vehicle (UAV) sử dụng 4 động cơ là những chủ đề được nghiên cứu và
quan tâm của nhiều tác giả. Sử dụng phương pháp Newton Euler cho mô tả mô hình toán học, bao gồm các
động lực học, khí động học và động lực học rotor được đề cập. Hệ chuyển động của thiết bị bay được chia
thành hai hệ thống con; Một hệ thống con cho chuyển động quay và một hệ thống con di chuyển (độ cao
và chuyển động theo các trục x và y). Quadrotor là một hệ thống 6 bậc tự do, bao gồm hệ thống quạt được
sử dụng như các phần tử tích cực, trong khi các hệ thống con cho chuyển động mang tính thụ động. Một
mô hình toán học đầy đủ phải đảm bảo kiểm soát được độ cao, các tư thế và vị trí của thiết bị bay trong
không gian. Chính vì vây bài báo trình bày một phương pháp sử dụng bộ điều khiển tự chỉnh PID mờ cho
điều khiển thiết bị bay cho phép kết hợp phương pháp điều khiển truyền thống và phương pháp điều khiển
thông minh. Các kết quả của bài báo dựa trên mô phỏng đã được thực hiện để qua đó đánh giá và so sánh
với các kết quả khác để có thể làm cơ sở cho các thực nghiệm cho mô hình thực tế sau này.

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6
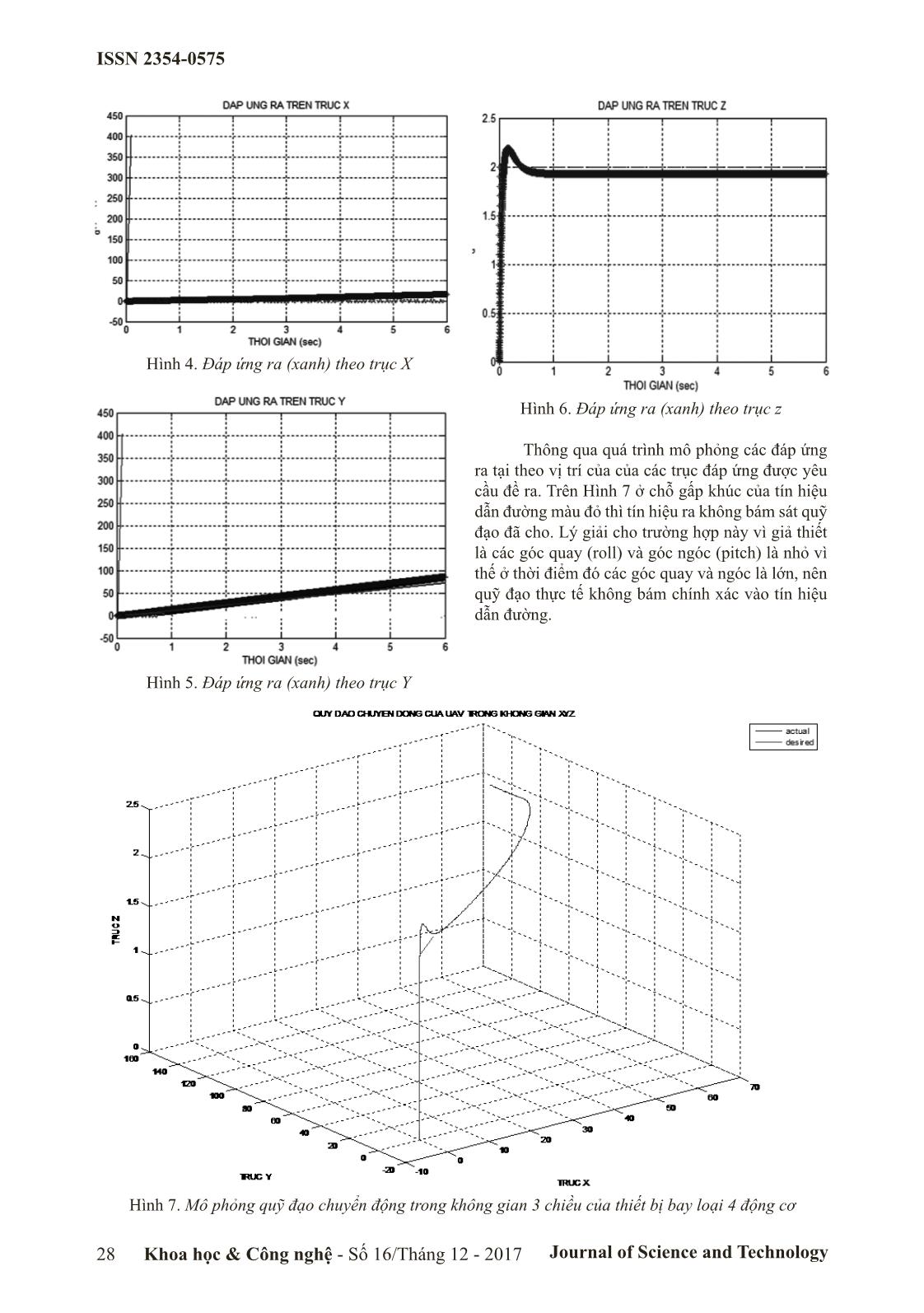
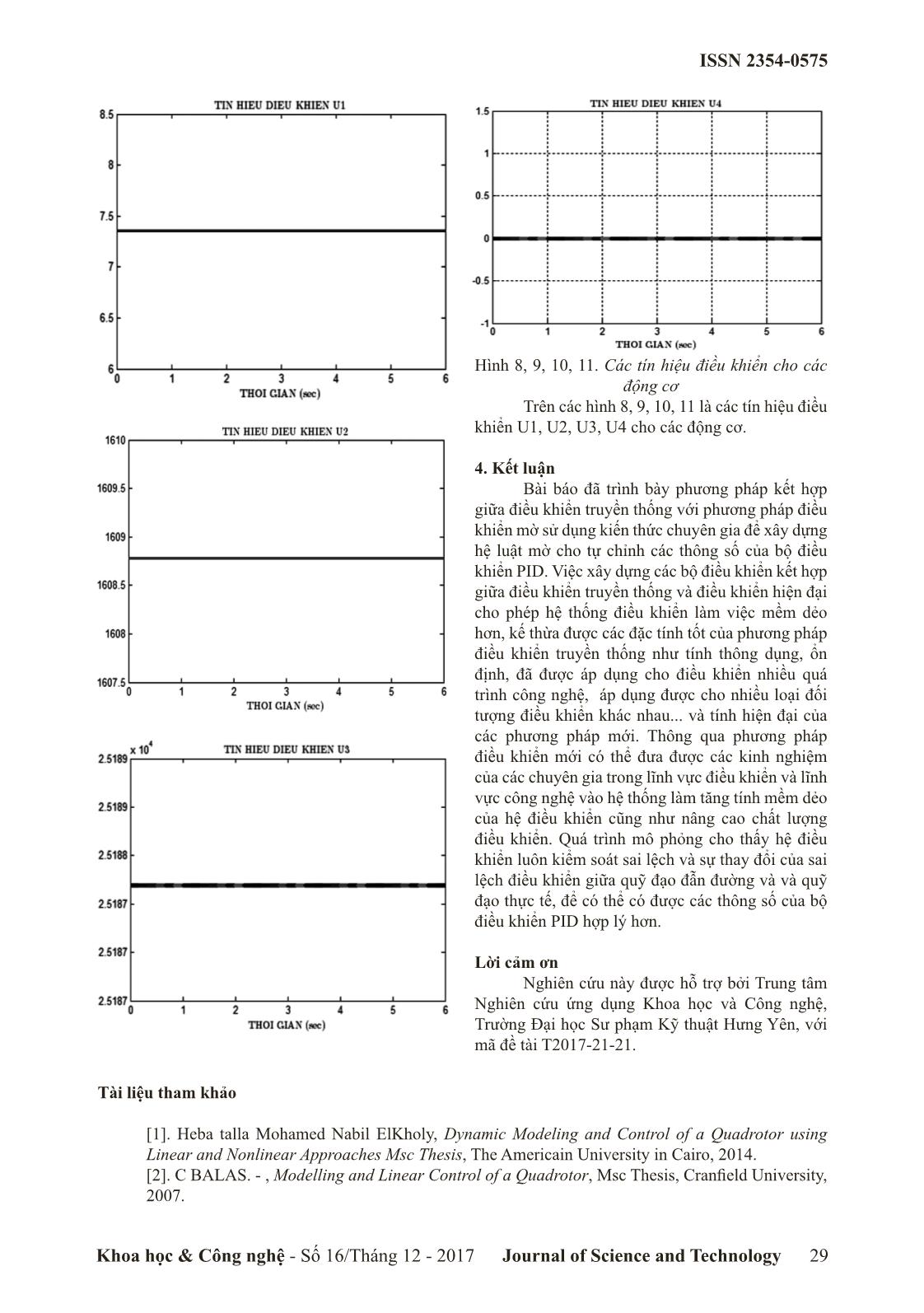
Tóm tắt nội dung tài liệu: Điều khiển thiết bị bay loại bốn động cơ sử dụng thuật toán điều khiển tự chỉnh PID mờ

cứu hiện đang tập trung phát triển các loại thiết bị bay nhỏ để sử dụng trong nghiên cứu và các ứng dụng thương mại. Các dạng mô hình toán học chi tiết cho thiết bị bay điều khiển từ xa, hay loại không người lái Unmanned Aerial Vehicle (UAV) sử dụng 4 động cơ là những chủ đề được nghiên cứu và quan tâm của nhiều tác giả. Sử dụng phương pháp Newton Euler cho mô tả mô hình toán học, bao gồm các động lực học, khí động học và động lực học rotor được đề cập. Hệ chuyển động của thiết bị bay được chia thành hai hệ thống con; Một hệ thống con cho chuyển động quay và một hệ thống con di chuyển (độ cao và chuyển động theo các trục x và y). Quadrotor là một hệ thống 6 bậc tự do, bao gồm hệ thống quạt được sử dụng như các phần tử tích cực, trong khi các hệ thống con cho chuyển động mang tính thụ động. Một mô hình toán học đầy đủ phải đảm bảo kiểm soát được độ cao, các tư thế và vị trí của thiết bị bay trong không gian. Chính vì vây bài báo trình bày một phương pháp sử dụng bộ điều khiển tự chỉnh PID mờ cho điều khiển thiết bị bay cho phép kết hợp phương pháp điều khiển truyền thống và phương pháp điều khiển thông minh. Các kết quả của bài báo dựa trên mô phỏng đã được thực hiện để qua đó đánh giá và so sánh với các kết quả khác để có thể làm cơ sở cho các thực nghiệm cho mô hình thực tế sau này. Từ khóa: Điều khiển mờ, Tập mờ, Logic mờ, PID, UAV. 1. Mở đầu Thiết bị bay loại 4 động cơ (Quadcopter) là một trong các đối tượng điều khiển được quan tâm nghiên cứu trong những năm gần đây và cũng là sở thích đam mê của nhiều tầng lớp dân cư, cũng như nghiên cứu khoa học. Thiết bị bay 4 động cơ có thiết kế đơn giản và chi phí thấp rất thích hợp cho các ứng dụng cứu hộ, cứu nạn, giám sát, quay phim, chụp ảnh từ trên cao Việc nghiên cứu, mô hình hoá và điều khiển các thiết bị bay loại 4 động cơ là một yêu cầu cần thiết. Thiết bị bay loại 4 động cơ là một hệ thống đa biến với 6 bậc tự do (DOF), và rất khó kiểm soát do sự ghép nối phi tuyến giữa các bộ truyền động và mức độ tự do của thiết bị [2]. Các thuật toán điều khiển bay phổ biến nhất hiện nay được sử dụng là các bộ điều khiển PID, các bộ điều khiển này chỉ có thể thực hiện khi quadrotor bay mang tính thử nghiệm với các điều kiện cụ thể nhất định. Để có thể áp dung rông rãi các thiết bị bay điều khiển từ xa hoặc không người lái cần thiết phải nghiên cứu xây đựng một bộ điều khiển, có khả năng xử lý các bậc tự do, cũng như với tác động của môi trường, bao gồm: các góc cuộn (roll) về trục x, là góc ngóc (pitch) về trục y, và góc nghiêng (yaw) về trục z. Hệ trục các góc quay (roll), góc ngóc (pitch) và góc nghiêng (yaw) được ký hiệu RPY. Tốc độ quay đồng bộ (Ω) của tất cả các động cơ là chìa khóa để kiểm soát quadrotor. Các kết quả chuyển động dọc theo z làm tăng hoặc giảm tốc độ quay của tất cả các rotor. Để thay đổi góc pitch ta tăng (giản) tốc độ của động cơ trước đồng thời giảm (tăng) tốc độ động cơ phía sau. Để thay đổi góc roll ta tăng (giảm) tốc độ động cơ bên phải và giảm (tăng) tốc độ của động cơ bên trái. Để thay đổi góc yaw ta tăng (giảm) tốc độ của cặp đôi động cơ phía trước và sau đồng thời giảm (tăng) tốc độ của cặp đôi động cơ phía phải trái. Chuyển động của quadrotor được mô tả bằng sơ đồ trong Hình 1. Có nhiều nghiên cứu đề cập qua sử dụng vị trí XYZ kết hợp với hướng cho phép giảm số lượng tính toán, giảm chi phí, giảm phần cứng đều khiển. [1, 2, 3, 4, 6] trong sử dụng bộ lọc Kalman mở rộng cho việc xây dựng mô hình điều khiển. Việc xử lý, tính toán dựa trên thông tin từ các bộ thu thập dữ liệu về gia tốc, con quay. Trong [1, 2, 4, 6] đề xuất một bộ lọc Kalman thông qua ước lượng trạng thái để có thể thích hợp cho UAV. [3, 4, 6, 7] đề cập đến một mô hình toán học phức tạp hơn, hệ thống điều khiển cũng được đề cập với thuật toán điều khiển dễ thực hiện trên một vi điều khiển truyền thống. 2. Mô hình toán học thiết bị bay loại bốn động cơ 2.1. Mô tả hệ thống Trên Hình 1 mô tả 6 bậc tự do của thiết bị ISSN 2354-0575 Journal of Science and Technology26 Khoa học & Công nghệ - Số 16/Tháng 12 - 2017 bay loại 4 động cơ. Với 3 biến x, y, z được sử dụng để diễn tả vị trí trong không gian XYZ, và ba góc Euler đại diện cho hướng của quadrotor, Φ được gọi là góc cuộn (roll) về trục x, θ là góc ngóc (pitch) về trục y, và góc ψ nghiêng (yaw) về trục z. Hệ động học của thiết bị bay loại 4 động cơ có thể được chia thành hai hệ thống con; Hệ thống con (RPY_roll, pitch và yaw) và hệ thống di chuyển theo vị trí (độ cao z và vị trí x và y). Hình 1. Hệ tọa độ đối với Quadrotor 2.1.1. Các hệ tọa độ Hệ tọa độ quán tính trái đất (Earth inertial frame) là hệ tọa độ I xyz có gốc tọa độ đặt một điểm trên trái đất (thường chọn là điểm cất cánh), trục I xx hướng theo hướng bắc, trục I yy hướng theo hướng đông và trục I zz vuông góc với mặt phẳng (I xy ). Hệ tọa độ của thiết bị (Body frame) là hệ tọa độ B xyz có gốc tọa độ B được đặt ở điểm đặt trọng tâm của quadrotor, trục B x hướng theo phía trước của quadrotor, trục B y vuông góc với trục B x và hướng sang phải của quadrotor, trục B z vuông góc với mặt phẳng B xy . 2.1.2. Động lực học của thiết bị bay loại bốn động cơ Khi nghiên cứu thiết bị bay thì lực đẩy và mô men tạo ra bởi tốc độ quay của cánh quạt có độ lớn tỉ lệ thuận với bình phương của tốc độ quay của cánh quạt. Theo Neuton_Euler có thể viết cho động học quay của hệ thiết bị bay [3,5] *J J J er r 3x ~ ~ ~ X= + +o _ i (1) Trong đó: τ vector cột của mô men xoắn dọc theo ba trục, J là ma trận quán tính đường chéo của 4 rotor, ω là vector cột với vận tốc góc, Jr là quán tính rotor, Ωr = Ω1 - Ω2 + Ω3 - Ω4 là tổng tốc độ rotor, e3 = [0 0 1] T mô tả định hướng rotor. Hệ động lực chuyển động so với hệ tọa độ mặt đất có thể viết [3]. mv mgeRT 3= -o (2) Trong đó: m là khối lượng của quadrotor, v là tốc độ di chuyển thể hiện qua vector cột, R là một ma trận quay mong muốn, T là vector cột của các lực. (T = [0 0 b(Ω1 2 + Ω2 2 + Ω3 2+ Ω 4 2)]T ); g là gia tốc trọng trường. Tín hiệu điều khiển cho bốn động cơ được miêu tả theo: U b U b U b U d 1 1 2 2 2 3 2 4 2 2 2 2 4 2 3 1 2 3 2 4 1 2 2 2 3 2 4 2 X X X X X X X X X X X X = + + + = - + = - = - + - + _ _ _ _ i i i i (3) Trong đó: U 1 , U 2 , U 3 , U 4 là các tín hiệu điều khiển từ động cơ. b và d là hệ số lực đẩy và kéo tương ứng. Tốc độ góc của chuyển động có thể viết [2, 3]: , , , , , cos cos cos sin cos sin sin cos sin sin sin cos I I I I I I I U I I I I I I l U I I I I U z g m U x m U y m U 1 x y z x r x y z x y r y z x y z 2 3 4 1 1 1 z i} i i z} z zi z i z i } z } z i } z } X X W = - - + = - - + = - + =- + = + = + p o o o p o o o p o o p p p d d d _ _ _ n n n i i i (4) Trong đó: Φ, θ và ψ là các góc cuộn, ngóc và góc nghiêng tương ứng; I x , I y , I z là mô men quán tính theo các trục x, y, và z Jr quán tính động cơ; Ω là vận tốc góc của rotor; l là chiều dài của cánh tay cánh quạt từ gốc của hệ tọa độ. 3. Thiết kế thuật toán điều khiển Các bộ điều khiển PID, bộ điều khiển toàn phương tuyến tính LQR, bộ điều khiển logic mờ, điều khiển bền vững và điều khiển phản hồi tuyến tính... được ứng dụng rộng rãi trong các nghiên cứu gần đây. Trong đó phổ biến nhất vẫn là sử dụng bộ ISSN 2354-0575 Khoa học & Công nghệ - Số 16/Tháng 12 - 2017 Journal of Science and Technology 27 điều khiển PID. Bộ điều khiển PID dựa trên sai số đo, thực sự đơn giản và dễ dàng áp dụng trong thực tế. Việc áp dụng tiêu chuẩn tối ưu khi lựa chọn 3 tham số Kp, Kd, Ki thường cho kết quả chấp nhận được. Sử dụng thuật điều khiển tự chỉnh cho chỉnh định các thông số K P , K D , K I giúp cho quá trình điều khiển mềm dẻo hơn, bởi vì quá trình chỉnh định các thông số K P , K D , K I được thực hiện theo hệ luật điều khiển mờ và hệ luật cho chỉnh định các thông số được xây dựng từ các kinh nghiệm của các chuyên gia điều khiển cũng như chuyên gia công nghệ trong lĩnh vực điều khiển thiết bị bay. 3.1. Thuật toán điều khiển tự chỉnh PID mờ Phương trình điều khiển PID cổ điển có dạng sau: ( ) ( ) ( ) ( )u t K e t K e t d K dt d e tp I t D0 x= + +# (5) Trong đó: K P , K I , K D là các hằng số tỷ lệ, tích phân và vi phân. e(t) là sai lệch điều khiển. 3.2. Chỉnh định các thông số Kp, Ki, Kd Việc chỉnh định các thông số K P , K D , K I sử dụng hệ luật mờ theo Mandani có dạng sau: if x is A and y is B then z is C (6) Với x, y, z là các biến và A, B, C là các giá trị ngôn ngữ, trong đó là phần điều kiện và là phần kết luận của luật. Tương ứng với đầu vào cho chỉnh định các thông số của luật (6) trong bộ điều khiển tự chỉnh PID mờ ta sử dụng đầu vào là sai lệch e và sự thay đổi của sai lệch ce thay cho x và y trong (6) và đầu ra là các hằng số K p , K I , K D . Các giá trị ngôn ngữ A, B, C trong (6) được lựa chọn là NB, NM, NS, ZO, PS, PM, PB tương đương với (NB) NegativeBig, (NM) Negative Medium, (NS) NegativeSmall, Zero (ZO), PositiveSmall (PS), PositiveMedium (PM), Positive Big (PB), xem Hình 2. NB NM NS ZE PS PM PB Hình 2. Các tập mờ cho đầu vào e(k) và c(k) Các thông số K p , K D , K I trong quá trình điều khiển thường thay đổi trong một khoảng Kpmin- Kpmax-, Kimin-Kimax, Kdmin- Kdmax. Việc xác định các giá trị cụ thể của K p , K D , K I trong khoảng đó được thực hiện theo luật mờ (7). Các luật mờ cho chỉnh định các thông số K p , K D , K I sẽ là một hệ luật xem Bảng 1 và Bảng 2 và tập mờ ở Hình 3 là các tập mờ cho chỉnh định các thông số K p , K D , K I . Bảng 1. Hệ luật cho chỉnh định K p , K I Error, e NB NM NS ZE PS PM PM C h g e E PB B B B B B B B PM S B B B B B S PS S S B B B S S ZE S S S B S S S NS S S B B B S S NMM S B B B B B S NB B B B B B B B Bảng 2. Hệ luật cho chỉnh định K D Error, e NB NM NS ZE PS PM PM C h g e E PB S S S S S S S PM B B S S S B B PS B B B S B B B ZE B B B B B B B NS B B B S B B B NMM B B S S S B B NB S S S S S S S Hình 3. Các tập mờ sử dụng trong chỉnh định các thông số Kp, Ki, Kd 3.3. Mô phỏng hệ thống điều khiển tự chỉnh PID Quá trình mô phỏng cho hệ thống điều khiển tự chỉnh các thông số Kp, Ki, Kd của bộ điều khiển PID được viết trên ngôn ngữ của Matlab dạng M-file với các thông số của thiết bị bay loại 4 đông cơ bao gồm: khối lượng thiết bị bay m = 2.35Kg, gia tốc trọng trường g = 9.81m/s2, quán tính cửa rotor theo trục x là Ix = 0.1676 kg.m2; quán tính cửa rotor theo trục y là Iy = 0.1686 kg.m2; quán tính cửa rotor theo trục z là Iz = 0.29743 kg.m2; l = 0.5 m; hệ số lực kéo b = 0.03N s2, hệ số lực đẩy d = 0.075N m s2. Trên các hình 4, 5, 6, 7 là các kết quả mô phỏng của thiết bị bay loại 4 động cơ. ISSN 2354-0575 Journal of Science and Technology28 Khoa học & Công nghệ - Số 16/Tháng 12 - 2017 Hình 4. Đáp ứng ra (xanh) theo trục X Hình 5. Đáp ứng ra (xanh) theo trục Y Hình 6. Đáp ứng ra (xanh) theo trục z Thông qua quá trình mô phỏng các đáp ứng ra tại theo vị trí của của các trục đáp ứng được yêu cầu đề ra. Trên Hình 7 ở chỗ gấp khúc của tín hiệu dẫn đường màu đỏ thì tín hiệu ra không bám sát quỹ đạo đã cho. Lý giải cho trường hợp này vì giả thiết là các góc quay (roll) và góc ngóc (pitch) là nhỏ vì thế ở thời điểm đó các góc quay và ngóc là lớn, nên quỹ đạo thực tế không bám chính xác vào tín hiệu dẫn đường. Hình 7. Mô phỏng quỹ đạo chuyển động trong không gian 3 chiều của thiết bị bay loại 4 động cơ ISSN 2354-0575 Khoa học & Công nghệ - Số 16/Tháng 12 - 2017 Journal of Science and Technology 29 Hình 8, 9, 10, 11. Các tín hiệu điều khiển cho các động cơ Trên các hình 8, 9, 10, 11 là các tín hiệu điều khiển U1, U2, U3, U4 cho các động cơ. 4. Kết luận Bài báo đã trình bày phương pháp kết hợp giữa điều khiển truyền thống với phương pháp điều khiển mờ sử dụng kiến thức chuyên gia để xây dựng hệ luật mờ cho tự chỉnh các thông số của bộ điều khiển PID. Việc xây dựng các bộ điều khiển kết hợp giữa điều khiển truyền thống và điều khiển hiện đại cho phép hệ thống điều khiển làm việc mềm dẻo hơn, kế thừa được các đặc tính tốt của phương pháp điều khiển truyền thống như tính thông dụng, ổn định, đã được áp dụng cho điều khiển nhiều quá trình công nghệ, áp dụng được cho nhiều loại đối tượng điều khiển khác nhau... và tính hiện đại của các phương pháp mới. Thông qua phương pháp điều khiển mới có thể đưa được các kinh nghiệm của các chuyên gia trong lĩnh vực điều khiển và lĩnh vực công nghệ vào hệ thống làm tăng tính mềm dẻo của hệ điều khiển cũng như nâng cao chất lượng điều khiển. Quá trình mô phỏng cho thấy hệ điều khiển luôn kiểm soát sai lệch và sự thay đổi của sai lệch điều khiển giữa quỹ đạo đẫn đường và và quỹ đạo thực tế, để có thể có được các thông số của bộ điều khiển PID hợp lý hơn. Lời cảm ơn Nghiên cứu này được hỗ trợ bởi Trung tâm Nghiên cứu ứng dụng Khoa học và Công nghệ, Trường Đại học Sư phạm Kỹ thuật Hưng Yên, với mã đề tài T2017-21-21. Tài liệu tham khảo [1]. Heba talla Mohamed Nabil ElKholy, Dynamic Modeling and Control of a Quadrotor using Linear and Nonlinear Approaches Msc Thesis, The Americain University in Cairo, 2014. [2]. C BALAS. - , Modelling and Linear Control of a Quadrotor, Msc Thesis, Cranfield University, 2007. ISSN 2354-0575 Journal of Science and Technology30 Khoa học & Công nghệ - Số 16/Tháng 12 - 2017 [3]. C. Nicol C.J.B. Macnab A. Ramirez-Serrano, ROBUST NEURAL NETWORK CONTROL OF A QUADROTOR HELICOPTER, Schulich School of Engineering, University of Calgary, 978-1-4244- 1643-1/08/$25©2008 IEEE. [4]. Bousbaine, Amar; Wu, Mian Hong; Poyi, Gwangtim Timothy, Modelling and Simulation of a Quad-rotor Helicopter, [5]. Jung J. W., Choi H. H., and Kim T. H., Fuzzy PD Speed Controller for Permanent Magnet Synchronous Motor, Journal of Power Electronics 11 (2011) 819-823. [6]. Qasim Muhammad, Attitude Control for a Quadrotor Helicopter, Msc Thesis, POLITECNICO DI MILANO. 2010. [7]. Iv ana Palunko and Rafael Fierro, Adaptive Control of a Quadrotor with Dynamic Changes in the Center of Gravity, Department of Electrical and Computer Engineering, University of New Mexico, Albuquer que NM, USA,978-3-902661-93-7/11/$20.00 © 2011 IFAC. CONTROL A QUADMOTOR USING A KIND OF FUZZY SELF - TUNING PID CONTROLLER Abstract: This paper proposes a Fuzzy tuning PID to control a quadrotor. This method is used for flight control that combines conventional control methods and intelligent control methods. The results of this paper based on simulations have been made in order to evaluate so that can be used as the basis for late experimental models. Keywords: Fuzzy control, Fuzzy set, Fuzzy Logic, PID, UAV.
File đính kèm:
 dieu_khien_thiet_bi_bay_loai_bon_dong_co_su_dung_thuat_toan.pdf
dieu_khien_thiet_bi_bay_loai_bon_dong_co_su_dung_thuat_toan.pdf

