Bài giảng Xử lý số tín hiệu - Đào Thị Thu Thủy
1.1 Tín hiệu, hệ thống và xử lý tín hiệu
1.2 Phân loại tín hiệu
1.3 Khái niệm tần số trong tín hiệu liên tục và tín
hiệu rời rạc thời gian
1.4 Biến đổi AD và DA6
1.1 Tín hiệu, hệ thống và xử lý tín hiệu
a. Khái niệm tín hiệu (signal)
Tín hiệu là biểu hiện vật lý của thông tin
9 Tín hiệu được biểu diễn một hàm theo một hay nhiều
biến số độc lập.
Ví dụ về tín hiệu:
9 Tín hiệu âm thanh, tiếng nói là sự thay đổi áp suất
không khí theo thời gian
9 Tín hiệu hình ảnh là hàm độ sáng theo 2 biến không
gian và thời gian
9 Tín hiệu điện là sự thay đổi điện áp, dòng điện theo thời
gian7
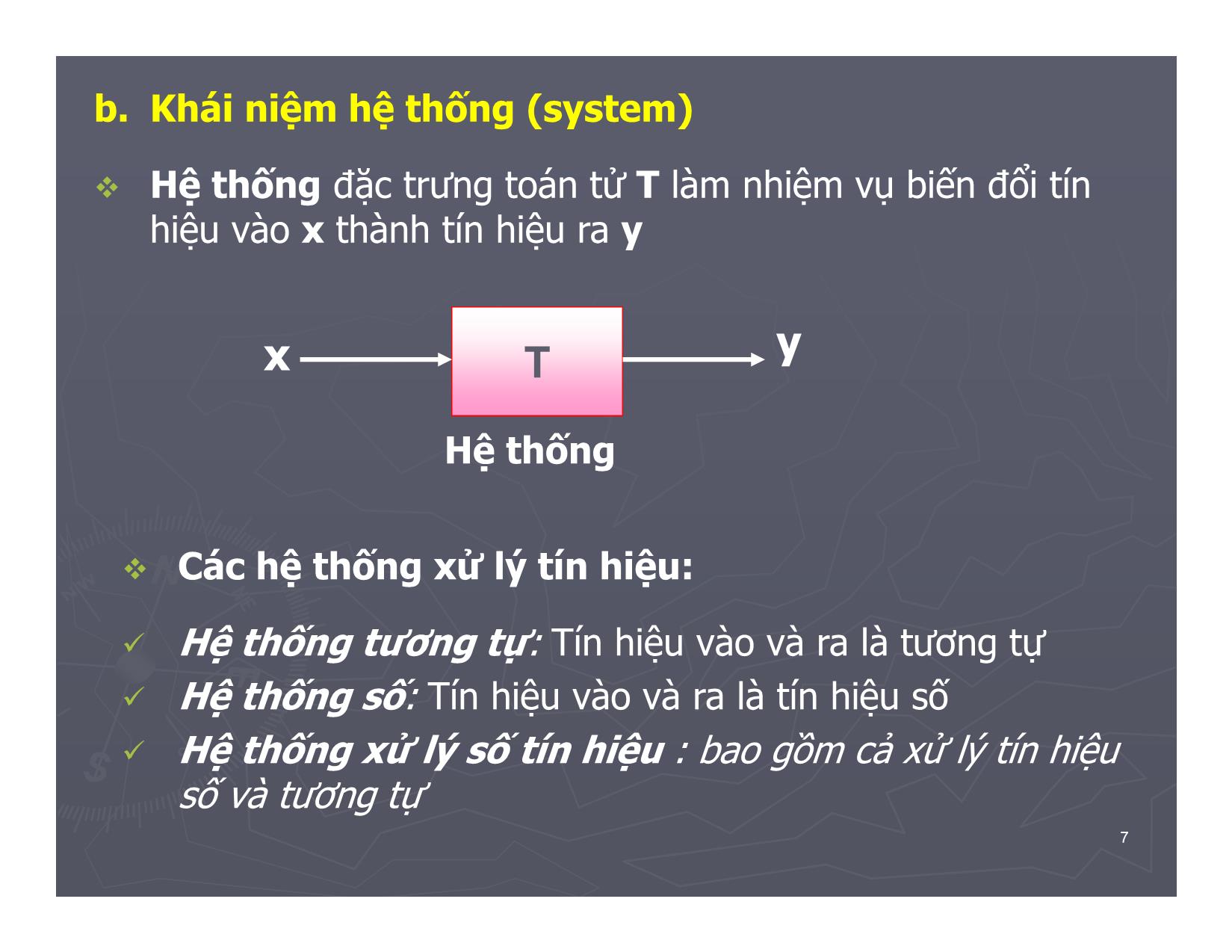
b. Khái niệm hệ thống (system)
Hệ thống đặc trưng toán tử T làm nhiệm vụ biến đổi tín
hiệu vào x thành tín hiệu ra y
x T y
Hệ thống
Các hệ thống xử lý tín hiệu:
9 Hệ thống tương tự: Tín hiệu vào và ra là tương tự
9 Hệ thống số: Tín hiệu vào và ra là tín hiệu số
9 Hệ thống xử lý số tín hiệu : bao gồm cả xử lý tín hiệu
số và tương t

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Xử lý số tín hiệu - Đào Thị Thu Thủy

xử lý
tiếp.
b. Lọc tiêu hủy
Là bộ lọc số thông thấp sau khi lấy mẫu quá mức
trước khi đưa tần số lấy mẫu giảm trở lại trị số
ban đầu, để bảo đảm là sự biệt danh không xuất
hiện trở lại. CNDT_DTTT 25
6.5 MẠCH KHÔI PHỤC TƯƠNG TỰ
►Mục đích của mạch khôi phục tương tự là
chuyển đổi các mẫu rời rạc x(nT) trở thành tín
hiệu tương tự xo(t).
►Dựa theo nguyên lý mạch lấy mẫu và giữ. Mỗi
mẫu được duy trì biên độ cho đến khi gặp mẫu
kế tiếp (mạch tái lập cầu thang) ta được tín
hiệu tương tự thô.
►Sau đó qua mạch hậu lọc (lọc thông thấp) có
tác dụng làm trơn tru dạng sóng tương tự thô.
CNDT_DTTT 26
CNDT_DTTT 27
Chương 7,8:
BIẾN ĐỔI FOURIER RỜI RẠC
BIẾN ĐỔI FOURIER NHANH
Giảng viên: Ths. Đào Thị Thu Thủy
Chương 7,8:
BIẾN ĐỔI FOURIER RỜI RẠC
BIẾN ĐỔI FOURIER NHANH
(BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG TRONG MIỀN TẦN SỐ
RỜI RẠC)
7.1 KHÁI NiỆM DFT
7.2 BIẾN ĐỔI FOURIER RỜI RẠC (DFT)
7.3 CÁC TÍNH CHẤT DFT
7.4 BiẾN ĐỔI FOURIER NHANH (FFT)
CNDT_DTTT 3
7.1 KHÁI NiỆM DFT
+∞
Biến đổi Fourier dãy x(n): X(ω )= ∑ x(n)e− jnω
n=−∞
X(ω) có các hạn chế khi xử lý trên thiết bị, máy tính:
► Tần số ω liên tục
► Độ dài x(n) là vô hạn: n biến thiên -∞ đến ∞
Khi xử lý X(Ω) trên thiết bị, máy tính cần:
► Rời rạc tần số ω -> ωK
► Độ dài x(n) hữu hạn là N: n = 0 ÷ N -1
⇒ Biến đổi Fourier của dãy có độ dài hữuhạntheotần
số rờirạc, gọitắtlàbiến đổiFourierrờirạc–DFT
(Discrete Fourier Transform)
7.2 BIẾN ĐỔI FOURIER RỜI RẠC - DFT
► DFT của x(n) có độ dài N định nghĩa:
2 π
⎧ N − 1 − j kn
⎪ ∑ x ( n )e N : 0 ≤ k ≤ N − 1
X ( k ) = ⎨ n = 0
⎪
⎩ 0 : k còn lại
N −1
2π ⎧ kn
− j ⎪ ∑ x(n)W N : 0 ≤ k ≤ N − 1
W = e N X (k ) = ⎨ n=0
N ⎪
⎩0 : k còn lại
► WN tuần hòan với độ dài N:
2π 2π
− j (r+mN ) − j r
(r+mN ) N N r
WN = e = e = WN
► X(k) biểu diễn dưới dạng modun & argument:
X(k) = X(k) e jϕ (k )
X(k) -phổ rời rạc biên độ
Trong đó:
ϕ(k) = arg[X(k)] -phổ rời rạc pha
2π
⎧ 1 N −1 j kn
⎪ ∑ X (k )e N : 0 ≤ n ≤ N − 1
► IDFT: x(n) = ⎨ N k = 0
⎪
⎩0 : n còn lại
► Cặp biến đổi Fourier rời rạc:
N −1
⎧ kn
⎪ X (k ) = ∑ x (n )W N : 0 ≤ k ≤ N − 1
⎪ n = 0
⎨ N −1
⎪ 1 − kn
x (n ) = ∑ X (k )W N : 0 ≤ n ≤ N − 1
⎩⎪ N k = 0
Ví dụ 7.1: Tìm DFT của dãy: x(n) = 1,2,3,4
{↑ }
3 2π
kn − j
X (k) = ∑ x(n)W4 1 4 2 3
n=0 W4 = e = − j;W4 = −1;W4 = j
3
0
X(0) = ∑ x(n)W4 = x(0) + x(1) + x(2) + x(3) = 10
n=0
3
n 1 2 3
X(1) = ∑ x(n)W4 = x(0) + x(1)W4 + x(2)W4 + x(3)W4 = −2 + j2
n=0
3
2n 2 4 6
X(2) = ∑ x(n)W4 = x(0) + x(1)W4 + x(2)W4 + x(3)W4 = −2
n=0
3
3n 3 6 9
X(3) = ∑ x(n)W4 = x(0) + x(1)W4 + x(2)W4 + x(3)W4 = −2 − j2
n=0
7.3 CÁC TÍNH CHẤT DFT
a) Tuyến tính
DFT DFT
► Nếu: x1(n)N ←⎯→⎯ X1(k)N x2(n)N ←⎯→⎯ X2(k)N
DFT
► Thì: a1x1(n)N + a2x2(n)N ←⎯→⎯ a1X1(k)N +a2X2(k)N
Nếu:L = N ≠ N = L Chọn:
x1 1 2 x2 N = max{N1, N2 }
b) Dịch vòng:
DFT
► Nếu: x(n)N ←⎯→⎯ X(k)N
DFT kn
► Thì: 0
x(n− n0 )N ←⎯→⎯ WN X(k)N gọi là dịch vòng của
~ x(n)N đi n0 đơn vị
Với: x(n− n0 )N = x(n− n0 )N rectN(n)
Ví dụ 7.2: Cho: x(n) = 1,2,3,4
{↑ }
a) Tìm dịch tuyến tính: x(n+3), x(n-2)
b)Tìm dịch vòng: x(n+3)4, x(n-2)4
x(n)
4
3
2
1 n
0 1 2 3
x(n+3) x(n-2)
4 4
3 3
a) 2 2
1 n 1 n
-3 -2 -1 0 0 1 2 3 4 5
x(n) x(n-1)4
b) 4 4
3 3
2 2
1
1 n n
0 1 2 3 0 1 2 3
N
x(n+1)4
4
x(n − 2)4 = 3,4,1,2
3 { ↑ }
2
1 n
x(n + 3)4 = { 4,1,2,3}
0 1 2 3 ↑
c) Chập vòng:
DFT DFT
► Nếu: x1(n)N ←⎯→⎯ X1(k)N x2(n)N ←⎯→⎯ X2(k)N
DFT
► Thì: x1(n)N ⊗x2(n)N ←⎯→⎯ X1(k)N X2(k)N
N−1
Chập vòng 2 dãy
Với: x1(n)N ⊗ x2(n)N = ∑x1(m)N x2(n−m)N
m=0 x1(n) & x2(n)
~
Và: x2 (n− m)N = x2 (n− m)N rectN (n) Dịch vòng dãy
x (-m) đi n đ/vị
Chập vòng có tính giao hóan: 2
x1(n)N ⊗ x2(n)N = x2(n)N ⊗ x1(n)N
Nếu:L = N ≠ N = L Chọn:
x1 1 2 x2 N = max{N1, N2 }
Ví dụ 7.3: Tìm chập vòng 2 dãy x1(n) = 2,3,4 x2 (n) = { 1,2,3,4}
{↑ } ↑
Chọn độ dài N: N1 = 3, N2 = 4 ⇒ N = max{N1, N2 } = 4
3
x3 (n)4 = x1 (n)4 ⊗ x2 (n)4 = ∑ x1 (m )4 x2 (n − m )4 : 0 ≤ n ≤ 3
m=0
Đổi biến n->m: x1(m) = { 2,3,4,0} x2 (m) = 1,2,3,4
↑ {↑ }
Xác định x (-m) : ~
2 4 x2 (−m)4 = x2 (−m)4 rect4(n) = 1,4,3,2
{↑ }
x2(m) x2(-m)
4 4
3 3
2 2
1 m 1 m
0 1 2 3 -3 -2 -1 0
~ ~
x2(−m) x2 (−m)4 = x2 (−m)rect4 (n)
4 4
3 3
2 2
1 1
m m
0 1 2 3
-3 -2 -1 0 1 2 3 4
Xác định x2(n-m) là dịch vòng của x2(-m) đi n đơn vị
n>0: dịch vòng sang phải, n<0: dịch vòng sang trái
x2(-m)4 x2(1-m)4
4 4
3 3
2 2
1 m 1 m
0 1 2 3 0 1 2 3
x2(2-m)4 x2(3-m)4
4 4
3 3
2 2
1 m 1 m
0 1 2 3 0 1 2 3
► Tìm biến đổi nghịch IDFT 10 điểm của
X(k) = 1 + 2δ(k) với 0 ≤ k ≤ 9
Nhân các mẫu 3
x1(m) & x2(n-m) x3 (n)4 = ∑ x1 (m)4 x2 (n − m)4 : 0 ≤ n ≤ 3
và cộng lại: m=0
3
n=0: x3 (0)4 = ∑ x1 (m )4 x2 (0 − m )4 = 26
m=0
3
n=1: x3 (1)4 = ∑ x1 (m )4 x2 (1 − m )4 = 23
m =0
3
n=2: x3 (2)4 = ∑ x1 (m )4 x2 (2 − m )4 = 16
m=0
3
n=3: x3 (3)4 = ∑ x1 (m )4 x2 (3 − m )4 = 25
m=0
Vậy: x3 (n)4 = x1 (n)4 ⊗ x2 (n)4 = { 26,23,16,25}
↑
7.4 BiẾN ĐỔI FOURIER NHANH FFT
7.4.1 KHÁI NiỆM BiẾN ĐỔI FOURIER NHANH FFT
Vào những nămthậpkỷ 60, khi công nghệ vi xử lý phát
triểnchưamạnh thì thờigianxử lý phép tóan DFT trên
máy tương đốichậm, do số phép nhân phứctương đối
lớn.
N −1
kn
DFT của x(n) có độ dài N: X (k) = ∑ x(n)W N : 0 ≤ k ≤ N − 1
n=0
Để tính X(k), với mỗi giá trị k cần có N phép nhân và (N-
1) phép cộng, vậy với N giá trị k thì cần có N2 phép nhân
và N(N-1) phép cộng.
Để khắcphụcvề mặttốc độ xử lý củaphéptínhDFT,
nhiềutácgiảđã đưaracácthuậttóanriêngdựatrên
DFT gọilàFFT (Fast Fourier Transform).
7.4.2 THUẬT TOÁN FFT CƠ SỐ 2
a. THUẬT TÓAN FFT CƠ SỐ 2 PHÂN THEO THỜI GIAN
► Giả thiết dãy x(n) có độ dài N=2M,nếu không có dạng lũy
thừa 2 thì thêm vài mẫu 0 vào sau dãy x(n).
► Thuật tóan dựatrênsự phân chia dãy vào x(n) thành các
dãy nhỏ,dobiến n biểuthị cho trụcthời gian nên gọilà
phân chia theo thời gian.
N −1 N −1 N −1
kn kn kn
X (k) = ∑ x(n)WN = ∑ x(n)WN + ∑ x(n)WN
n=0 n=0,2,4... n=1,3,5...
► Thay n=2r vớinchẵnvàn=2r+1 vớinlẽ:
( N / 2)−1 ( N / 2)−1
2kr k (2r +1)
X (k) = ∑ x(2r)W N + ∑ x(2r + 1)W N
r=0 r=0
2π 2π
j k 2r j kr
Do: k 2r N N / 2 kr
WN = e = e = WN / 2
( N / 2)−1 ( N / 2)−1
kr k kr
X (k) = ∑ x(2r)W N / 2 + W N . ∑ x(2r + 1)W N / 2
r=0 r=0
(N / 2)−1 (N / 2)−1
Đặt: kr kr
X0(k) = ∑ x(2r)WN / 2 X1(k) = ∑ x(2r +1)WN / 2
r=0 r=0
k
X (k) = X 0 (k) + WN .X1(k)
► X0(k) –DFTcủaN/2điểm ứng vớichỉ số nchẵn
► X1(k) –DFTcủaN/2điểm ứng vớichỉ số nlẽ
► Lấyvídụ minh họa cho x(n) vớiN=8
Phân chia DFT- N điểm -> 2 DFT- N/2 điểm;
X0(0)
x(0) X(0)
W0
X0(1)
x(2) DFT X(1)
n chẵn W1
N/2 X0(2)
x(4) X(2)
W2
điểm X0(3)
x(6) X(3)
W3
X1(0)
x(1) X(4)
W4
X1(1)
x(3) DFT X(5)
n lẽ W5
N/2 X1(2)
x(5) X(6)
W6
điểm X1(3)
x(7) X(7)
W7
► Qui ước cách tính X(k) theo lưu đồ:
- Nhánh ra của 1 nút bằng tổng các nhánh vào nút đó
-Giátrị mỗi nhánh bằng giá trị nút xuất phát nhân hệ số
► Sau đó đánh lạichỉ số theo thứ tự các mẫux(n),tiếptục
phân chia DFT củaN/2điểm thành 2 DFT củaN/4điểm
theo chỉ số nchẵnvàlẽ và cứ thế tiếptục phân chia cho
đến khi nào còn DFT 2 điểmthìdừng lại.
► Ví dụ X0(k) được phân chia:
( N / 2)−1 ( N / 2)−1
kr kr
X0(k) = ∑ x(2r)WN / 2 = ∑ g(r)WN / 2
r=0 r=0
( N / 2)−1 ( N / 2)−1
kr kr
= ∑ g(r)WN / 2 + ∑ g(r)WN / 2
r=0,2,4... r=1,3,5...
( N / 4)−1 ( N / 4)−1
kl k kl
= ∑ g(2l)WN / 4 +WN / 2 ∑ g(2l + 1)WN / 4
l=0 l=0
k
= X00(k) +WN / 2 .X01(k)
Phân chia DFT- N/2 điểm -> 2 DFT- N/4 điểmcủaX0(k)
X (0)
00 X (0)
x(0) DFT 0
0
X00(1) W N/2
x(4) N/4 X0(1)
1
W N/2
X01(0)
x(2) X0(2)
DFT 2
W N/2
X01(1)
x(6) N/4 X0(3)
3
W N/2
X (k) = X (k) + W k .X (k)
Phân chia X1(k) tương tự: 1 10 N / 2 11
X (0)
10 X (0)
x(1) DFT 1
0
X10(1) W N/2
x(5) N/4 X1(1)
1
W N/2
X11(0)
x(3) X1(2)
DFT 2
W N/2
X11(1)
x(7) N/4 X1(3)
3
W N/2
Lưu đồ DFT dãy x(n) sau 2 lần phân chia vớiN=8
X00(0)
x(0) DFT X(0)
0 W0
X00(1) W
x(4) N/4 X(1)
1
X (0) W2 W
x(2) 01 X(2)
DFT 4 2
X (1) W W
x(6) N/4 01 X(3)
W6 W3
X10(0)
x(1) DFT X(4)
W0 W4
X10(1)
x(5) N/4 X(5)
W2 W5
X11(0)
x(3) X(6)
DFT W4 W6
X11(1)
x(7) N/4 X(7)
W6 W7
x(0) X (0)
Lưu đồ DFT 00
W0 =1
2 điểm: N
x(4) N/2 X00(1)
WN =-1
Lưu đồ DFT dãy x(n) sau 3 lần phân chia vớiN=8
x(0) X(0)
W0 W0
x(4) X(1)
-1 W2 W1
x(2) X(2)
W4 W2
x(6) X(3)
-1 W6 W3
x(1) X(4)
W0 W4
x(5) X(5)
-1 W2 W5
x(3) X(6)
W4 W6
x(7) X(7)
-1 W6 W7
X (p) X (p)
m m+1 Xm(p) Xm+1(p)
r
W N
Wr
X (q) X (q) N
m m+1 Xm(q) X (q)
(r+N/2) r m+1
WN = - WN -1
Lưu đồ DFT dãy x(n) sau 3 lần phân chia vớiN=8
x(0) X(0)
x(4) X(1)
-1 W0
x(2) X(2)
W2 -1
x(6) X(3)
Đảo -1 -1
bít W0
x(1) X(4)
-1
W1
x(5) X(5)
-1 -1
W0 W2
x(3) X(6)
-1
W2 -1 W3
x(7) X(7)
-1 -1 -1
► Với N=2M -> M lần phân chia
► Số phép nhân = số phép cộng = NM/2=(N/2)log2N
Ví dụ : Hãy vẽ lưu đồ và tính FFT cơ số 2 phân theo t/g
x ( n ) = 1,2 ,3 ,4
{↑ }
x(0) X(0)
x(2) X(1)
-1 W0
x(1) X(2)
W1 -1
x(3) X(3)
-1 -1
k=0: X(0) = [x(0) + x(2)] + W0[x(1) + x(3)] = 10.
k=1: X(1) = [x(0) - x(2)] + W1[x(1) - x(3)] = - 2 +
j2.
k=2: X(2) = [x(0) + x(2)] - W0[x(1) + x(3)] = - 2.
k=3: X(3) = [x(0) - x(2)] - W1[x(1) - x(3)] = - 2 - j2.
Bảng mô tả qui luật đảobít:
Chæ soá Soá nhò phaân chöa Soá nhò phaân ñaûo Chæ soá
töï nhieân ñaûo (n2,n1,n0) (n0,n1,n2) ñaûo
0 0 0 0 0 0 0 0
1 0 0 1 1 0 0 4
2 0 1 0 0 1 0 2
3 0 1 1 1 1 0 6
4 1 0 0 0 0 1 1
5 1 0 1 1 0 1 5
6 1 1 0 0 1 1 3
7 1 1 1 1 1 1 7
b. THUẬT TÓAN FFT CƠ SỐ 2 PHÂN THEO TẦN SỐ
► Thuậttóandựatrênsự phân chia dãy ra X(k) thành các
dãy nhỏ,dobiến k biểuthị cho trụctầnsố nên gọilà
phân chia theo tầnsố.
N −1 ( N / 2)−1 N −1
kn kn kn
X (k) = ∑ x(n)WN = ∑ x(n)W N + ∑ x(n)W N
n=0 n=0 n= N / 2
( N / 2)−1 ( N / 2)−1
kn k (n+ N / 2)
= ∑ x(n)W N + ∑ x(n + N / 2)W N
n=0 n=0
( N / 2)−1 ( N / 2)−1
kn kN / 2 kn
= ∑ x(n)WN + WN ∑ x(n + N / 2)WN
n=0 n=0
( N / 2)−1
k kn
= ∑ []x(n) + (−1) x(n + N / 2) WN
n=0
► Với k chẵn, thay k=2r:
(N/2)− 1
rn
X(2r)=++∑ [] x(n) x(n N / 2) WN/2
n0=
► Với k lẽ, thay k=2r+1
( N / 2)−1
n rn
X (2r + 1) = ∑ {[]x(n) − x(n + N / 2) W N }W N / 2
n=0
► Đặt: g(n)= x(n)+ x(n+ N/2); h(n)= x(n)− x(n+ N/2)
( N / 2)−1 (N / 2)−1
rn n rn
X (2r) = ∑ g(n)WN / 2 X(2r +1) = ∑ [h(n)WN ]WN / 2
n=0 n=0
► X(2r) –DFTcủaN/2điểm ứng vớichỉ số k chẵn
► X(2r+1) –DFTcủaN/2điểm ứng vớichỉ số k lẽ
Phân chia DFT N=8 điểm->2DFTN/2=4điểm
g(0)
x(0) X(0)
g(1)
x(1) DFT X(2)
g(2) N/2 k chẵn
x(2) X(4)
g(3) điểm
x(3) X(6)
h(0) W0
x(4) X(1)
-1 1
h(1) W
x(5) DFT X(3)
-1 2
h(2) W N/2 k lẽ
x(6) X(5)
-1 3
h(3) W điểm
x(7) X(7)
-1
► Sau đó đánh lạichỉ số theo thứ tự các mẫu X(k), tiếptục
phân chia DFT củaN/2điểm thành 2 DFT củaN/4điểm
theo chỉ số kchẵnvàlẽ.Tiếptục phân chia cho đếnkhi
nào còn DFT 2 điểmthìdừng lại.
► Dữ liệuraX(k)đượcsắpxếptheothứ tựđảo bít, còn
dữ liệuvàođượcsắp theo thứ tự tự nhiên.
► Số phép nhân và phép cộng trong lưu đồ phân theo tần
số bằng vớisố phép nhân và cộng trong lưu đồ phân
theo thời gian.
Lưu đồ DFT dãy x(n) sau 3 lần phân chia vớiN=8
x(0) X(0)
x(1) X(4)
W0 -1
x(2) X(2)
-1 W2
x(3) X(6)
-1 -1 Đảo
W0 bít
x(4) X(1)
-1
W1
x(5) X(5)
-1 -1
W2 W0
x(6) X(3)
-1
W3 -1 W2
x(7) X(7)
-1 -1 -1
Ví dụ 4.4.2: Hãy vẽ lưu đồ và tính FFT cơ số 2 phân theo t/s
x ( n ) = 1,2 ,3 ,4
{↑ }
x(0) X(0)
x(1) X(2)
-1
0
x(2) W X(1)
-1 W1
x(3) X(3)
-1 -1
► k=0: X(0) = [x(0) + x(2)] + [x(1) + x(3)] = 10.
► k=2: X(2) = [x(0) + x(2)] - [x(1) + x(3)] = - 2.
► k=1: X(1) = [x(0) - x(2)] + W1[x(1) - x(3)] = - 2 +
j2.
► k=3: X(3) = [x(0) - x(2)] - W1[x(1) - x(3)] = - 2 - j2.
7.4.3 THUẬT TOÁN FFT VỚI N=N1N2
► Giả thiết độ dài dãy x(n) có thể phân tích N=N1N2,nếu
độ dài không thể biểudiễndướidạng trên thì thêm vài
mẫu 0 vào sau dãy x(n).
► Giả thiếtdữ liệuvàođượcsắpxếp vào trong mảng theo
thứ tự từng cộtvớisố cột N1 và số hàng N2:
n2 n1 01N1-1
0 x(0) x(N2)x[N2(N1-1)]
1 x(1) x(N2+1) x[N2(N2-1)+1]
N2-1 x(N2-1) x(2N2-1) x[N1N2-1]
► Lấyvídụ sắpxếp dãy x(n) với N=12, chọnN1=3 và N2=4
n2 n1 012
0 x(0) x(4) x(8)
1 x(1) x(5) x(9)
2 x(2) x(6) x(10)
3 x(3) x(7) x(11)
► Các chỉ số n của x(n), k củaX(k)xácđịnh:
0 ≤ n1 ≤ N1-1
► n=n1N2 +n2
0 ≤ n2 ≤ N2-1
0 ≤ k1 ≤ N1 -1
► k=k1 +k2N1
0 ≤ k2 ≤ N2 -1
► DFT N điểm dãy x(n) được phân tích:
N2 −1 N1−1
(k1+k2N1 )(n2 +n1N2 )
X(k) = X(k1 + k2 N1 ) = ∑∑x(n2 + n1N2 )WN
n2=0 n1=0
N2 −1 N1 −1
n2k1 n1k1N 2 n2k2 N1 n1k2 N1N 2
= ∑∑x(n2 + n1 N 2 )WN WN WN WN
n2=0 n1 =0
Do:WnkN11 2== W nk 11 ;W n 2 k 2 N 1 W n 2 k 2 ;W nk 12 NN 1 2 = 1
NNNNN12
N 2 −1 ⎪⎧⎡ N1 −1 ⎤ ⎪⎫
⇒ X (k) = x(n + n N )W n1k1 W n2k1 W n2k2
∑∑⎨⎢ 2 1 2 N1 ⎥ N ⎬ N 2
n2=0 ⎩⎪⎣ n1 =0 ⎦ ⎭⎪
N1 −1
F(n ,k ) = x(n + n N )W n1k1
2 1 ∑ 2 1 2 N1
► Đặt: n1 =0
n2k1
G(n2 ,k1 ) = F(n2 ,k1 ).WN
N 2 −1
X (k) = G(n ,k )W n2k2
∑ 2 1 N 2
n2=0
Các bướctiếnhànhthuật tóan:
► Sắpxếpdữ liệu vào theo thứ tự từng cột, mảng x
► Tính DFT theo từng hàng mảng x, được F(n2,k1)
n2k1
► Tính mảng hệ số WN
n2k1
► Nhân mảng F(n2,k1) với WN , được G(n2,k1)
► Tính DFT theo từng cộtmảng G(n2,k1), được X(k)
► Đọcdữ liệu ra theo thứ tự từng hàng X(k).
Ví dụ : Nêu các bước tính và vẽ lưu đồ thuật tóan FFT dãy
x(n) với N=N1N2=12, chọn N1=3 và N2=4
► Sắp xếp dữ liệu vào theo thứ tự từng cột như bảng:
n2 n1 012
0 x(0) x(4) x(8)
1 x(1) x(5) x(9)
2 x(2) x(6) x(10)
3 x(3) x(7) x(11)
► Tính DFT theo từng hàng mảng x, được F(n2,k1):
N1 −1
F (n ,k ) = x(n + n N )W n1k1
2 1 ∑ 2 1 2 N1
n1 =0
n2 k1 012
0 F(0,0) F(0,1) F(0,2)
1 F(1,0) F(1,1) F(1,2)
2 F(2,0) F(2,1) F(2,2)
3 F(3,0) F(3,1) F(3,2)
n2k1
► Tính mảng hệ số WN
n2 k1 012
0 0 0
0 WN WN WN
0 1 2
1 WN WN WN
0 2 4
2 WN WN WN
0 3 6
3 WN WN WN
► Nhân các phần tử mảng F(n2,k1) với các hệ số của
n2k1
mảng WN tương ứng, được G(n2,k1) :
nikj
Phầntử: G(ni,kj)=F(ni,kj). WN
n2 k1 012
0 G(0,0) G(0,1) G(0,2)
1 G(1,0) G(1,1) G(1,2)
2 G(2,0) G(2,1) G(2,2)
3 G(3,0) G(3,1) G(3,2)
► Tính DFT theo từng cột mảng G(n2,k1), được X(k):
N 2 −1
X (k) = X (k + N k ) = G(n ,k )W n2k2
1 1 2 ∑ 2 1 N 2
n2 =0
k2 k1 012
0 X(0) X(1) X(2)
1 X(3) X(4) X(5)
2 X(6) X(7) X(8)
3 X(9) X(10) X(11)
► Đọc dữ liệu ra theo thứ tự từng hàng X(k)
Lưu đồ FFT dãy x(n) N=N1N2,vớiN1=3, N2=4:
X(0)
x(0) DFT
DFT X(3)
x(4) N1
điểm N2
x(8) điểm X(6)
0
W X(9)
x(1) DFT
W1
x(5) N1 X(1)
W2
x(9) điểm DFT X(4)
0
W N2
x(2) X(7)
DFT W2 điểm
x(6) N X(10)
1 W4
x(10) điểm X(2)
W0
x(3) DFT X(5)
DFT 3
W N2
x(7) N1 X(8)
W6 điểm
x(11) điểm X(11)File đính kèm:
 bai_giang_xu_ly_so_tin_hieu_dao_thi_thu_thuy.pdf
bai_giang_xu_ly_so_tin_hieu_dao_thi_thu_thuy.pdf

