Bài giảng Toán rời rạc - Chương: Tìm kiếm trên đồ thị - Trần Vĩnh Đức
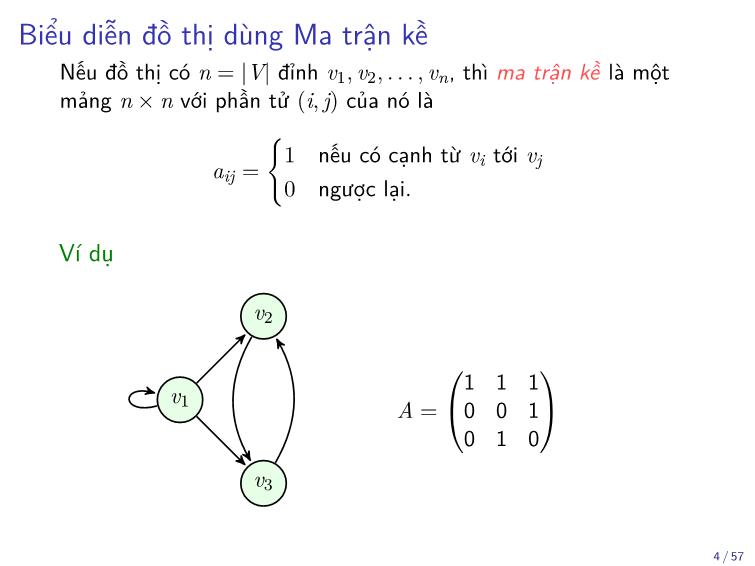
Dùng ma trận kề có hiệu quả?
▶ Có thể kiểm tra có cạnh nối giữa cặp đỉnh bất kỳ chỉ cần một
lần truy cập bộ nhớ.
▶ Tuy nhiên, không gian lưu trữ là O(n2)
5 / 57Biểu diễn đồ thị dùng danh sách kề
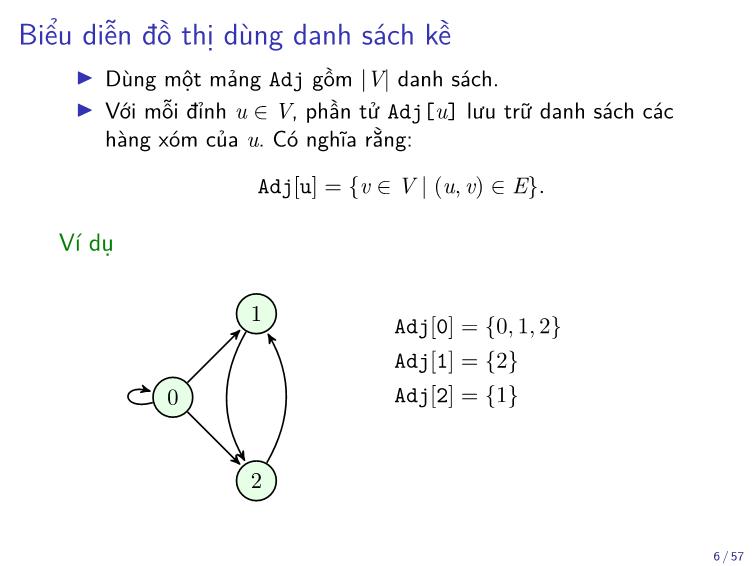
▶ Dùng một mảng Adj gồm jVj danh sách.
▶ Với mỗi đỉnh u 2 V, phần tử Adj[u] lưu trữ danh sách các
hàng xóm của u. Có nghĩa rằng:
Adj[u] = fv 2 V j (u; v) 2 Eg:
Ví dụ
Adj[0] = f0; 1; 2g
Adj[1] = f2g
Adj[2] = f1g

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5
Trang 6

Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương: Tìm kiếm trên đồ thị - Trần Vĩnh Đức", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương: Tìm kiếm trên đồ thị - Trần Vĩnh Đức

tor; they therefore lead to a node that has already been completely Xét vi là đỉnh đầu tiên trong C explored (that is, already postvisited). Tree được thăm theo DFS. Mọi đỉnh C D Cross khác trong chu trình sẽ đạt được từ vi. Vậy thì vi−1 → vi là back edge. Figure 3.7 has two forward edges, two back edges, and two cross edges. Can you spot them? 28 / 57 Ancestor and descendant relationships, as well as edge types, can be read off directly from pre and post numbers. Because of the depth-first exploration strategy, vertex u is an ancestor of vertex v exactly in those cases where u is discovered first and Bài tập 1. Hãy mô tả một thuật toán kiểm tra liệu đồ thị có hướng cho trước có chu trình hay không. 2. Hãy cài đặt thuật toán này. 29 / 57 Đồ thị phi chu trình và sắp xếp topo ▶ Đồ thị phi chu trình (DAG) cho phép sắp thứ tự các đỉnh sao cho: Có cạnh (u, v) nếu và chỉ nếu u đứng trước v. ▶ Cách sắp thứ tự các đỉnh này gọi là sắp xếp topo. ▶ DAG cho phép mô hình hiệu quả các bài toán liên quan đến quan hệ nhân quả, phân cấp, phụ thuộc thời gian. ▶ Ví dụ: Mỗi môn học có môn tiên quyết (môn cần học trước). Một cách lựa chọn thứ tự học các môn là một cách sắp topo. 30 / 57 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 90 3.3 Depth-first search in directed graphs Đồ thị phi chu trình (DAG) Figure 3.8 A directed acyclic graph with one source, two sinks, and four possible linearizations. A C E B D F Phi chu trình ⇐⇒ Không có Back Edge ⇐⇒ Sắp topo out of bed; you have to be out of bed, but not yet dressed, to take a shower; and so on). The question then is, what is a valid order in which to perform the tasks? Such constraints are conveniently represented by a directed graph in which each task is a node, andu to therev if u isis an a precondition edge from for31v / 57. In other words, before performing a task, all the tasks pointing to it must be completed. If this graph has a cycle, there is no hope: no ordering can possibly work. If on the other hand the graph is a dag, we would like if possible to linearize (or topologically sort) it, to order the vertices one after the other in such a way that each edge goes from an earlier vertex to a later vertex, so that all precedence constraints are satisfied. In Figure 3.8, for instance, one valid ordering is B, A, D, C , E , F . (Can you spot the other three?) What types of dags can be linearized? Simple: All of them. And once again depth- first search tells us exactly how to do it: simply perform tasks in decreasing or- der of their post numbers. After all, the only edges (u, v) in a graph for which post(u) <post(v) are back edges (recall the table of edge types on page 88)—and we have seen that a dag cannot have back edges. Therefore: Property In a dag, every edge leads to a vertex with a lower post number. This gives us a linear-time algorithm for ordering the nodes of a dag. And, to- gether with our earlier observations, it tells us that three rather different-sounding properties—acyclicity, linearizability, and the absence of back edges during a depth- first search—are in fact one and the same thing. Since a dag is linearized by decreasing post numbers, the vertex with the smallest post number comes last in this linearization, and it must be a sink—no outgoing edges. Symmetrically, the one with the highest post is a source, a node with no incoming edges. Property Every dag has at least one source and at least one sink. The guaranteed existence of a source suggests an alternative approach to lineariza- tion: P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 90 3.3 Depth-first search in directed graphs FigureBài 3.8 tậpA directed acyclic graph with one source, two sinks, and four possibleHãy linearizations. đưa ra mọi cách sắp topo cho đồ thị phi chu trình sau: A C E B D F out of bed; you have to be out of bed, but not yet dressed, to take a shower; and so on). The question then is, what is a valid order in which to perform the tasks? Such constraints are conveniently represented by a directed graph in which each task is a node, andu to therev if u isis an a precondition edge from for v. In other 32 / 57 words, before performing a task, all the tasks pointing to it must be completed. If this graph has a cycle, there is no hope: no ordering can possibly work. If on the other hand the graph is a dag, we would like if possible to linearize (or topologically sort) it, to order the vertices one after the other in such a way that each edge goes from an earlier vertex to a later vertex, so that all precedence constraints are satisfied. In Figure 3.8, for instance, one valid ordering is B, A, D, C , E , F . (Can you spot the other three?) What types of dags can be linearized? Simple: All of them. And once again depth- first search tells us exactly how to do it: simply perform tasks in decreasing or- der of their post numbers. After all, the only edges (u, v) in a graph for which post(u) <post(v) are back edges (recall the table of edge types on page 88)—and we have seen that a dag cannot have back edges. Therefore: Property In a dag, every edge leads to a vertex with a lower post number. This gives us a linear-time algorithm for ordering the nodes of a dag. And, to- gether with our earlier observations, it tells us that three rather different-sounding properties—acyclicity, linearizability, and the absence of back edges during a depth- first search—are in fact one and the same thing. Since a dag is linearized by decreasing post numbers, the vertex with the smallest post number comes last in this linearization, and it must be a sink—no outgoing edges. Symmetrically, the one with the highest post is a source, a node with no incoming edges. Property Every dag has at least one source and at least one sink. The guaranteed existence of a source suggests an alternative approach to lineariza- tion: Tính chất của DAG Mệnh đề Trong DAG, nếu (u, v) ∈ E thì post(u) > post(v). Vậy thì các đỉnh của DAG có thể sắp topo theo thứ tự giảm dần của post. 33 / 57 Bài tập Xét một DAG có pre và post như dưới đây. Hãy đưa ra một thứ tự topo cho các đỉnh. 1 6 0 : [1, 16] 1 : [17, 18] 0 8 2 : [2, 9] 3 : [3, 8] 4 : [19, 20] 7 4 5 : [4, 7] 6 : [11, 14] 7 : [10, 15] 5 2 8 : [12, 13] 9 : [5, 6] 9 3 34 / 57 Bài tập 1. Hãy mô tả một thuật toán sắp Topo cho một DAG. 2. Hãy cài đặt thuật toán này. 35 / 57 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 90 3.3 Depth-first search in directed graphs Đỉnh nguồn và đỉnh hút Figure 3.8 A directed acyclic graph with one source, two sinks, and four possible linearizations. A C E B D F Trong đồ thị có hướng, out of bed;▶ youĐỉnh have nguồn to be(source) out of bed, là đỉnh but không not yet có dressed, cạnh đi to vào. take a shower; and so on). The question then is, what is a valid order in which to perform the tasks? ▶ Đỉnh hút (sink) là đỉnh không có cạnh đi ra. Such constraints are conveniently represented by a directed graph in which each task is a node, andu to therev if u isis an a precondition edge from for v. In other words, before performing a task, all the tasks pointing to it must be completed. If this graph has a cycle, there is no hope: no ordering can possibly work. If on the other 36 / 57 hand the graph is a dag, we would like if possible to linearize (or topologically sort) it, to order the vertices one after the other in such a way that each edge goes from an earlier vertex to a later vertex, so that all precedence constraints are satisfied. In Figure 3.8, for instance, one valid ordering is B, A, D, C , E , F . (Can you spot the other three?) What types of dags can be linearized? Simple: All of them. And once again depth- first search tells us exactly how to do it: simply perform tasks in decreasing or- der of their post numbers. After all, the only edges (u, v) in a graph for which post(u) <post(v) are back edges (recall the table of edge types on page 88)—and we have seen that a dag cannot have back edges. Therefore: Property In a dag, every edge leads to a vertex with a lower post number. This gives us a linear-time algorithm for ordering the nodes of a dag. And, to- gether with our earlier observations, it tells us that three rather different-sounding properties—acyclicity, linearizability, and the absence of back edges during a depth- first search—are in fact one and the same thing. Since a dag is linearized by decreasing post numbers, the vertex with the smallest post number comes last in this linearization, and it must be a sink—no outgoing edges. Symmetrically, the one with the highest post is a source, a node with no incoming edges. Property Every dag has at least one source and at least one sink. The guaranteed existence of a source suggests an alternative approach to lineariza- tion: Tính chất của DAG Mệnh đề (Nhắc lại) Trong DAG, nếu (u, v) ∈ E thì post(u) > post(v). Vậy thì các đỉnh của DAG có thể sắp topo theo thứ tự giảm dần của post. Và khi đó, đỉnh có post nhỏ nhất sẽ nằm cuối danh sách, và vậy thì nó phải là đỉnh hút. Tương tự, đỉnh có post lớn nhất là đỉnh nguồn. 37 / 57 Mệnh đề Mọi DAG đều có ít nhất một đỉnh nguồn và ít nhất một đỉnh hút. Bài tập Hãy chứng minh mệnh đề trên. 38 / 57 Thuật toán sắp topo (thứ 2) ▶ Tìm một đỉnh nguồn, ghi ra nó, và xóa nó khỏi đồ thị. ▶ Lặp lại cho đến khi đồ thị trở thành rỗng. 39 / 57 Thuật toán sắp topo (thứ 2) ▶ Tìm một đỉnh nguồn, ghi ra nó, và xóa nó khỏi đồ thị. ▶ Lặp lại cho đến khi đồ thị trở thành rỗng. 40 / 57 Thuật toán sắp topo (thứ 2) ▶ Tìm một đỉnh nguồn, ghi ra nó, và xóa nó khỏi đồ thị. ▶ Lặp lại cho đến khi đồ thị trở thành rỗng. 41 / 57 Thuật toán sắp topo (thứ 2) ▶ Tìm một đỉnh nguồn, ghi ra nó, và xóa nó khỏi đồ thị. ▶ Lặp lại cho đến khi đồ thị trở thành rỗng. 42 / 57 Bài tập Chạy thuật toán sắp topo trên đồ thị sau: 1. Chỉ ra số pre và post của mỗi đỉnh. 2. Tìm các đỉnh nguồn và đỉnh hút của đồ thị. 3. Tìm thứ tự topo theo thuật toán. 4. Đồ thị này có bao nhiêu thứ tự topo? 43 / 57 Câu hỏi ▶ Tại sao thuật toán trước cho một thứ tự topo? ▶ Nếu đồ thị có chu trình thì thuật toán gặp vấn gì? ▶ Làm thế nào để cài đặt thuật toán này trong thời gian tuyến tính? 44 / 57 Nội dung Biểu diễn đồ thị Tìm kiếm theo chiều sâu trên đồ thị vô hướng Tìm kiếm theo chiều sâu trên đồ thị có hướng Thành phần liên thông mạnh Thành phần liên thông mạnh Định nghĩa Hai đỉnh u và v của một đồ thị có hướng là liên thông nếu có một đường đi từ u tới v và một đường đi từ v tới u. Quan hệ này phân hoạch tập đỉnh V thành các tập rời nhau và ta gọi các tập rời nhau này là các thành phần liên thông mạnh. 46 / 57 P1: OSO/OVY P2: OSO/OVY QC: OSO/OVY T1: OSO das23402 Ch03 GTBL020-Dasgupta-v10 August 10, 2006 19:18 Chapter 3 Algorithms 91 Find a source, output it, and delete it from the graph. Repeat until the graph is empty. Can you see why this generates a valid linearization for any dag? What happens if the graph has cycles? And, how can this algorithm be implemented in linear time? (Exercise 3.14.) 3.4 Strongly connected components 3.4.1 Defining connectivity for directed graphs Connectivity in undirected graphs is pretty straightforward: a graph that is not con- nected can be decomposed in a natural and obvious manner into several connected components (Figure 3.6 is a case in point). As we saw in Section 3.2.3, depth-first search does this handily, with each restart marking a new connected component. In directed graphs, connectivity is more subtle. In some primitive sense, the directed graph of Figure 3.9(a) is “connected”—it can’t be “pulled apart,” so to speak, with- out breaking edges. But this notion is hardly interesting or informative. The graph cannot be considered connected, because for instance there is no path from G to B or from F to A. The right way to define connectivity for directed graphs is this: Two nodes u and v of a directed graph are connected if there is a path from u to v and a path from v to u. ThànhFigure phần 3.9 (a) liên A directed thông graph mạnh and its strongly connected components. (b) The meta-graph. (a) (b) A B C D E F A B,E C,F G H G,H,I D J,K,L I J K L Hình: (a) Đồ thị có hướng và các thành phần liên thông mạnh. (b) Các thành phần liên thông mạnh tạo thành một DAG 47 / 57 Các thành phần liên thông mạnh trong đồ thị Mệnh đề Mọi đồ thị có hướng đều là một DAG của các thành phần liên thông mạnh. Vì nếu có chu trình đi qua một số thành phần liên thông mạnh thì các thành phần này phải được gộp chung lại thành một thành phần liên thông mạnh. 48 / 57 Một số tính chất Mệnh đề Nếu thủ tục con explore bắt đầu từ một đỉnh u, thì nó sẽ kết thúc khi mọi đỉnh có thể đến được từ u đã được thăm. 49 / 57 Một số tính chất Nếu ta gọi explore từ một đỉnh thuộc một thành phần liên thông mạnh hút, vậy thì ta sẽ nhận được đúng thành phần này. 50 / 57 Câu hỏi 1. Làm thế nào ta có thể tìm được một đỉnh mà ta chắc chắn nó thuộc vào thành phần liên thông mạnh hút? 2. Ta sẽ tiếp tục thế nào khi đã tìm được một thành phần liên thông mạnh? 51 / 57 Câu hỏi 1 Làm thế nào ta có thể tìm được một đỉnh mà ta chắc chắn nó thuộc vào thành phần liên thông mạnh hút? Xét GR là đồ thị ngược của G, tức là đồ thị GR đạt được từ G bằng cách đảo hướng các cạnh. Thành phần liên thông mạnh của G cũng là của GR. Tại sao? Và thành phần liên thông mạnh hút trong G sẽ là thành phần liên thông mạnh nguồn trong GR. Mệnh đề Đỉnh có số post lớn nhất theo DFS phải thuộc một thành phần liên thông mạnh nguồn. 52 / 57 Hình: Đồ thị G Hình: Đồ thị ngược GR của G 53 / 57 Câu hỏi 2 Ta sẽ tiếp tục thế nào khi đã tìm được một thành phần liên thông mạnh? Mệnh đề Nếu C và D là các thành phần liên thông mạnh, và có một cạnh từ một đỉnh trong C tới một đỉnh trong D, vậy thì số post lớn nhất trong C phải lớn hơn số post lớn nhất trong D. Khi ta tìm thấy một thành phần liên thông mạnh và xóa nó khỏi đồ thị G, vậy thì đỉnh với số post lớn nhất trong các đỉnh còn lại sẽ thuộc vào thành phần liên thông mạnh hút của đồ thị còn lại của G. 54 / 57 Thuật toán tìm thành phần liên thông mạnh 1. Chạy DFS trên đồ thị ngược GR của G. 2. Chạy thuật toán tìm thành phần liên thông (tương tự như của đồ thị vô hướng) trên đồ thị có hướng G; và trong khi chạy DFS, xử lý các đỉnh theo thức tự giảm dần theo số post của mỗi đỉnh (tìm được theo bước 1). 55 / 57 Bài tập Chạy thuật toán tìm thành phần liên thông mạnh trên đồ thị sau. 56 / 57 Bài tập Chạy thuật toán tìm thành phần liên thông mạnh trên đồ thị sau. 57 / 57
File đính kèm:
 bai_giang_toan_roi_rac_chuong_tim_kiem_tren_do_thi_tran_vinh.pdf
bai_giang_toan_roi_rac_chuong_tim_kiem_tren_do_thi_tran_vinh.pdf

