Giáo trình Phương pháp tính - Chương 2: Giải gần đúng phương trình đại số và siêu việt

nên:	 khi k ® ¥ 
vậy:	 khi k ® ¥ 
Nghĩa là :	
	Nếu phương trình vi phân gồm n+1 hệ số, một nghiệm riêng yk có thể được xác định từ n giá trị yk-1, yk-2,...,yn-1. Điều cho phép tính toán bằng cách 
truy hồi các nghiệm riêng của phương trình vi phân.
	Để tính nghiệm lớn nhất của đa thức, ta xuất phát từ các nghiệm riêng y1 = 0, y1 = 0,.., yn =1 để tính yn+1. Cách tính này được tiếp tục để tính yn+2 xuất phát từ y1 = 0, y2 = 0,..,yn+1 và tiếp tục cho đến khi yk+1/yk không biến đổi nữa. Trị số của yk+n được tính theo công thức truy hồi :
	(4)
Ví dụ: Tính nghiệm của đa thức Pn(x) = P3(x) = x3 - 10x2 + 31x - 30. 
Như vậy ao = 1, a1 = -10,a2 = 31 và a3 = -30.
Phương trình sai phân tương ứng là :
yk+3 -10yk+2 + 31yk+1 - 30yk = 0
Ta cho trước các giá trị y1 = 0; y2 = 0 và y3 = 1. Theo (4) ta tính được :
y4 = - (-10y3 + 31y2 - 30y1) = 10
y5 = - (-10y4 + 31y3 - 30y2) = 69
y6 = - (-10y5 + 31y5 - 30y3) = 410
y7 = - (-10y6 + 31y5 - 30y4) = 2261
y8 = - (-10y7 + 31y6 - 30y5) = 11970
y9 = - (-10y8 + 31y7 - 30y6) = 61909
y10 = - (-10y9 + 31y8 - 30y8) = 315850
y11 = - (-10y10 + 31y9 - 30y8) = 1598421
y12 = - (-10y11 + 31y10 - 30y9) = 8050130
y13 = - (-10y12 + 31y11 - 30y10) = 40425749
y14 = - (-10y13 + 31y12 - 30y11) = 202656090
y15 = - (-10y14 + 31y13 - 30y12) = 1014866581
y16 = - (-10y15 + 31y14 - 30y13) = 5079099490
y17 = - (-10y16 + 31y15 - 30y14) = 24409813589
y18 = - (-10y17 + 31y16 - 30y15) = 127092049130
y19 = - (-10y18 + 31y17 - 30y16) = 635589254740
Tỉ số các số yk+1/yk lập thành dãy :
	10 ; 6.9 ; 5.942 ; 5.5146 ; 5.2941 ; 5.172 ; 5.1018 ; 5.0607 ; 5.0363 ; 5.0218 ; 5.013 ; 5.0078 ; 5.0047 ; 5.0028 ; 5.0017 ; 5.001 
nghĩa là chúng sẽ hội tụ tới nghiệm lớn nhất là 5 của đa thức.
Chương trình 2-7
//phuong phap Bernoulli
#include 
#include 
#include 
#include 
#define max 50
void main()
 {
	float a[max],y[max];
	int k,j,i,n,l;
	float s,e1,e2,x0,x1,x;
	clrscr();
	printf("Cho bac cua da thuc can tim nghiem n = ");
	scanf("%d",&n);
	e1=1e-5;
	printf("Cho cac he so cua da thuc can tim nghiem\n");
	for (i=0;i<=n;i++)
	 {
	printf("a[%d] = ",i);
	scanf("%f",&a[i]);
	 }
	for (k=0;k<=n;k++)
	 a[k]=a[k]/a[0];
	 tt: x1=0;
	for (k=2;k<=n;k++)
	 y[k]=0;
	y[1]=1;
	l=0;
	do
	 {
	l=l+1;
	s=0;
	for (k=1;k<=n;k++)
	 s=s+y[k]*a[k];
	y[0]=-s;
	x=y[0]/y[1];
	e2=fabs(x1 - x);
	x1=x;
	for (k=n;k>=1;k--)
	y[k]=y[k-1];
	 }
	while((l=e1));
	if(e2>=e1)
	 {
	printf("Khong hoi tu");
	getch();
	exit(1);
	 }
	else
	 printf("Nghiem x = %.4f\n",x);
	n=n-1;
	if (n!=0)
	 {
	a[1]=a[1]+x;
	for (k=2;k<=n;k++)
	 a[k]=a[k]+x*a[k-1];
	goto tt;
	 }
	getch();
 }
Kết quả nghiệm của đa thức x3 - 10x2 + 31x - 30 là:5 ; 3 và 2
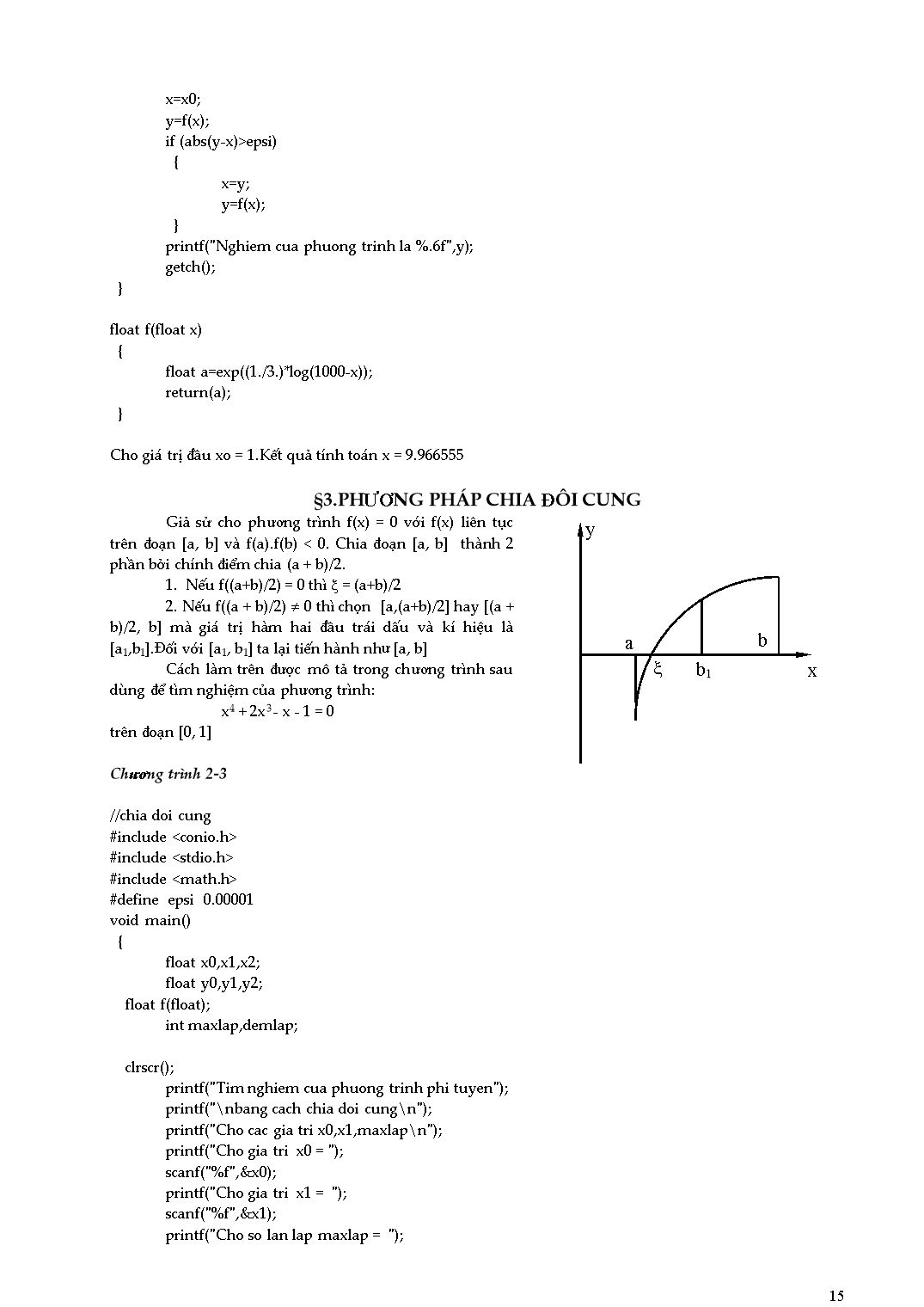
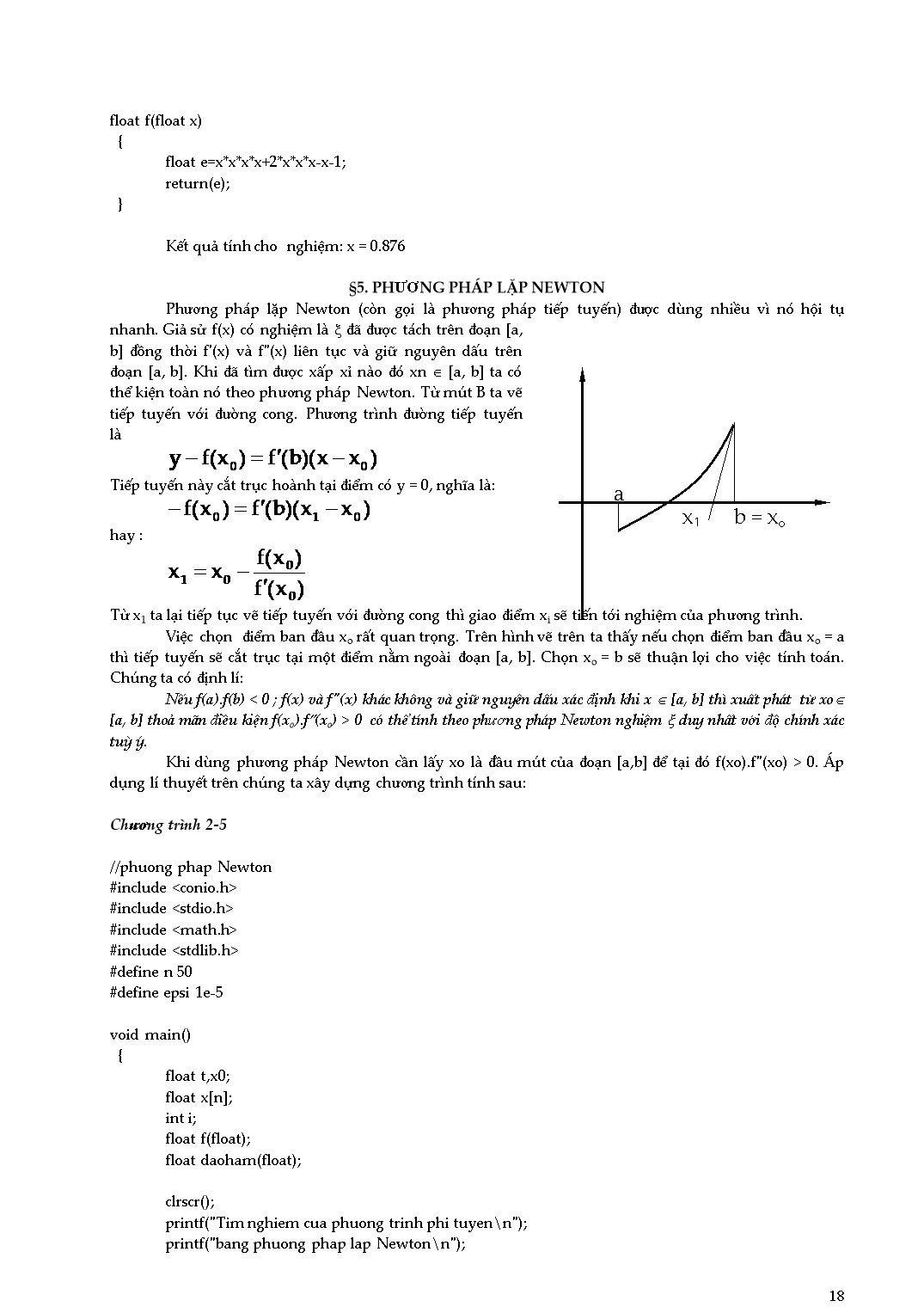
§8. PHƯƠNG PHÁP LẶP BIRGE - VIETTE 
	Các nghiệm thực, đơn giản của một đa thức Pn(x) được tính toán khi sử dụng phương pháp Newton	
	(1)
Để bắt đầu tính toán cần chọn một giá trị ban đầu xo. Chúng ta có thể chọn một giá trị xo nào đó, ví dụ :
và tính tiếp các giá trị sau :	
Tiếp theo có thể đánh giá Pn(xi) theo thuật toán Horner :
P0 = a0
	P1 = P0xi + a1	 	(2)
	P2 = P1xi + a2
	P3 = P2xi + a3
 	..................
	P(xi) = Pn = Pn-1xi + an
Mặt khác khi chia đa thức Pn(x) cho một nhị thức (x - xi) ta được :
Pn(x) = (x - xi)Pn-1(x) + bn	(3)
với bn = Pn(xi). Đa thức Pn-1(x) có dạng:
	Pn-1(x) = boxn-1 + b1xn-2 + p3xn-3 +..+ bn-2x + bn-1	(4)
Để xác định các hệ số của đa thức (4) ta thay (4) vào (3) và cân bằng các hệ số với đa thức cần tìm nghiệm Pn(x) mà các hệ số ai đã cho:
	(x - xi)( boxn-1 + b1xn-2+b3xn-3 +..+ bn-2x + bn-1 ) + bn
	= aoxn + a1xn-1 + a2xn-2 +...+ an-1x + a=	(5)
Từ (5) rút ra :
bo = ao
b1 = a1 + boxi	(6)
	b2 = a2 + b1xi
	......
	bk = ak + bk-1xi
	.......
	bn = an + bn-1xi = Pn(xi)
	Đạo hàm (3) ta được :
và:	(7)
	Như vậy với một giá trị xi nào đó theo (2) ta tính được Pn(xi) và kết hợp (6) với (7) tính được P¢n(xi). Thay các kết quả này vào (1) ta tính được giá trị xi+1. Quá trình được tiếp tục cho đến khi | xi+1 - xi | < e hay Pn(xi+1) » 0 nên a1 » xi+1 là một nghiệm của đa thức.
	Phép chia Pn(x) cho (x - a1) cho ta Pn-1(x) và một nghiệm mới khác được tìm theo cách trên khi chọn một giá trị xo mới hay chọn chính xo=a1. Khi bậc của đa thức giảm xuống còn bằng 2 ta dùng các công thức tìm nghiệm của tam thức để tìm các nghiệm còn lại.
Ví dụ: Tìm nghiệm của đa thức P3(x) = x3 - x2 -16x + 24 
ao = 1	a1 = -1	a2= -16	a3 = 24
Chọn xo = 3.5 ta có :
Po = ao = 1
P1 = a1 + pox0 = -1 + 3.5*1 = 2.5	
P2 = a2 + p1x0 = -16 + 3.5*2.5 = -7.25
P3 = a3 + p2x0 = 24 + 3.5*(-7.25) = - 1.375
b0 = a0 = 1;
b1 = a1 + box0 = -1 + 3.5*1 = 2.5	
b2 = a2 + b1x0 = -16 + 3.5*2.5 = -7.25
P2(3.5) = b0x2 + b1x + b2 = 13.75
Lặp lại bước tính trên cho x1 ta có:
Po = ao = 1
P1 = a1 + pox1 = -1 + 3.6*1 = 2.6	
P2 = a2 + p1x1 = -16 + 3.6*2.6 = -6.64
P3 = a3 + p2x1 = 24 + 3.6*(-6.64) = - 0.096
bo = ao = 1
b1 = a1 + box1 = -1 + 3.6*1 = 2.6	
b2 = a2 + p1x1 = -16 + 3.6*2.6 = -6.64
P2(3.6) = b0x2 + b1x + b2 = 15.68
Quá trình cứ thế tiếp tục cho đến khi sai số chấp nhận được. Chương trình dưới đây mô tả thuật tính trên.
Chương trình 2-8
//phuong phap Birge-Viette
#include 
#include 
#include 
#define max 20
void main()
 {
	float a[max],p[max],d[max],x[max];
	int k,j,i,n;
	float e1,e2,x0,x1;
	clrscr();
	printf("Cho bac cua da thuc n = ");
	scanf("%d",&n);
	e1=0.0001;
	printf("Cho cac he so cua da thuc can tim nghiem\n");
	for (i=0;i<=n;i++)
	 {
	printf("a[%d] = ",i);
	scanf("%f",&a[i]);
	 }
	x0=a[0];
	for (i=0;i<=n;i++)
	 a[i]=a[i]/x0;
	printf("Nghiem cua phuong trinh : \n");
	tt:x0=-a[n]/a[n-1];
	j=0;
	do
	 {
	j=j+1;
	p[1]=x0+a[1];
	d[1]=1.0;
	for (k=2;k<=n;k++)
	 {
	p[k]=p[k-1]*x0+a[k];
	d[k]=d[k-1]*x0+p[k-1];
	 }
	x1=x0-p[n]/d[n];
	e2=fabs(x1-x0);
	if (e2>e1)
	x0=x1;
	 }
	while((j=e1));
if (e2>=e1)
	 printf("Khong hoi tu");
	else
	 printf(" x = %.4f\n",x1);
	n=n-1;
	if (n!=0)
	 {
	for (k=1;k<=n;k++)
	 a[k]=p[k];
	goto tt;
	 }
	getch();
 }
	Dùng chương trình trên để tìm nghiệm của đa thức x4 + 2x3 - 13x2 - 14x + 24 ta được các nghiệm là:-4 ; 3 ; -2 và 1.
§9. PHƯƠNG PHÁP NGOẠI SUY AITKEN
	Xét phương pháp lặp :
	x = f(x)	(1)
với f(x) thoả mãn điều kiện hội tụ của phép lặp, nghĩa là với mọi xÎ [a, b] ta có:
| f’(x) | £ q < 1	(2)
Như vậy :
	xn+1 = f(xn)	(3)
	xn = f(xn-1)	(4)
Trừ (3) cho (4) và áp dụng định lí Lagrange cho vế phải với c Î [a, b] ta có :
	xn+1- xn = f(xn) - f(xn-1) = (xn - xn-1)f’(c)	(5)
Vì phép lặp (1) nên :
	| xn+1- xn | £ q | xn - xn-1 |	(6)
b = an - pb-2
Chúng ta nhận thấy rằng a được tính toán xuất phát từ cùng một công thức truy hồi như các hệ số bk và tương ứng với hệ số bn-1
	bn-1 = an-1 + sbn-2 - pbn-3 = a
Hệ số bn là :
	bn = an + sbn-1 - pbn-2 = sbn-1 + b
và cuối cùng :
	R1(x) = ax + b = b+-1(x - s) + bn
	Ngoài ra các hệ số bi phụ thuộc vào s và p và bây giờ chúng ta cần phải tìm các giá trị đặc biệt s* và p* để cho bn-1 và bn triệt tiêu. Khi đó r1(x)= 0 và nghiệm của tam thức x2 - s*x + p*x sẽ là nghiệm của đa thức Pn(x). Ta biết rằng bn-1 và bn là hàm của s và p :
	bn-1 = f(s, p)
	bn = g(s, p)
Việc tìm s* và p* đưa đến việc giải hệ phương trình phi tuyến:
Phương trình này có thể giải dễ dàng nhờ phương pháp Newton. Thật vậy với một phương trình phi tuyến ta có công thức lặp:	
xi+1 = xi - f(xi)/f'(xi) 
hay	f'(xi)(xi+1 - xi) = -f(xi)
Với một hệ có hai phương trình,công thức lặp trở thành:
	J(Xi)(Xi+1 - Xi) = -F(Xi)
với 	Xi = { si, pi}T và 	Xi+1 = { si+1, pi+1}T
Quan hệ : J(Xi)DX = -F(Xi) với DX = {si+1 - si,pi+1 - pi}T tương ứng với một hệ phương trình tuyến tính hai ẩn số Ds = si+1 - si và Dp = pi+1 - pi :
Theo công thức Cramer ta có :
Để dùng được công thức này ta cần tính được các đạo hàm ,,,. Các đạo hàm này được tính theo công thức truy hồi.
Do bo = ao nên 
b1 = a1 + sbo nên	
b2 = a2 + sb1- pbo nên 	
Mặt khác :	
nên: 	
b3 = a3 + sb2- pb1 nên:	
Nếu chúng ta đặt :
thì :	
co = bo	(2)
	c1 = b1 + sbo = b1 + sco
	c2 = b2 + sc1 - pco
	....................
	ck = bk + sck-1 - pck-2
	cn-1 = bn-1 + scn-2 - pcn-3
Như vậy các hệ số cũng được tính theo cách như các hệ số bk. Cuối cùng với f = bn-1 và g = bn ta được:	
	(3)
	(4)
	Sau khi phân tích xong Pn(x) ta tiếp tục phân tích Pn-2(x) theo phương pháp trên. Các bước tính toán gồm:
	- Chọn các giá trị ban đầu bất kì s0 và p0
	- Tính các giá trị bo,..,bn theo (1)
	- Tính các giá trị co,...,cn theo (2)
	- Tính Dso và Dpo theo (3) và (4)
	- Tính s1 = s0 + Dso và p1 = po+ Dpo
	- Lặp lại bước 1 cho đến khi pi+1 = pi = p và si+1 = si = s
	- Giải phương trình x2 - sx + p để tìm 2 nghiệm của đa thức
- Bắt đầu quá trình trên cho đa thức Pn-2(x)
Ví dụ: Tìm nghiệm của đa thức P4(x) = x4 - 1.1x3 + 2.3x2 + 0.5x2 + 3.3.
Với lần lặp ban đầu ta chọn s = -1 và p =1, nghĩa là tam thức có dạng: x2+x+1
	a0	a1	a2	a3	a4
	1	-1.1	2.3	0.5	3.3
 sbi	-1	2.1	-3.4	0.8
 -pbi-1	-1	2.1	-3.4
 bi	1	-2.1	3.4	-0.8 = bn-1	0.7=bn
 sbi	-1.0	3.1	-5.5
 -pbi-1	-1.0	3.1
	ci	1	-3.1	 5.5	-3.2
s* = -1 + 0.11 = -0.89
p* = 1 + 0.06 = 1.06
Tiếp tục lặp lần 2 với s1 = s* và p1 = p* ta có :
a0	a1	a2	a3	a4
	1	-1.1	2.3	0.5	3.3
 sbi	-0.89	1.77	-2.68	0.06
 -pbi-1	-1.06	2.11	-3.17
 bi	1	-1.99	3.01	-0.07 = bn-1	0.17=bn
 sbi	-0.89	2.56	-4.01
 -pbi-1	-1.0	 3.1
	ci	1	-2.88	4.51	-1.03
s* = -0.89 - 0.01 = -0.9
p* = 1.06 + 0.04 = 1.1
Như vậy: 	
P4(x) = (x2 + 0.9x + 1.1)(x2 + 2x + 3)
Chương trình sau áp dụng lí thuyết vừa nêu để tìm nghiệm của đa thức.
Chương trình 2-10
//phuong phap Bairstow
#include 
#include 
#include 
#include 
#define m 10
void main()
 {
	float a[m],b[m],c[m];
	int i,n,v;
	float s,e1,t,p,q,r,p1,q1;
	clrscr();
	printf("Cho bac cua da thuc n = ");
	scanf("%d",&n);
	printf("Cho cac he so cua da thuc can tim nghiem\n");
	for (i=n;i>=0;i--)
	 {
	printf("a[%d] = ",n-i);
	scanf("%f",&a[i]);
	 }
	printf("\n");
	e1=0.0001;
	if (n<=2)
	 if (n==1)
	{
	 printf("Nghiem cua he\n");
	 printf("%.8f",(a[0]/(-a[1])));
	 getch();
	 exit(1);
	}
	do
	 {
	v=0;
	p=1;
	q=-1;
	b[n]=a[n];
	c[n]=a[n];
	do
	 {
	b[n-1]=b[n]*p+a[n-1];
	c[n-1]=b[n-1]+b[n]*p;
	for (i=n-2;i>=0;i--)
	 {
	b[i]=b[i+2]*q+b[i+1]*p+a[i];
	c[i]=c[i+2]*q+c[i+1]*p+b[i];
	 }
	r=c[2]*c[2]-c[1]*c[3];
	p1=p-(b[1]*c[2]-b[0]*c[3])/r;
	q1=q-(b[0]*c[2]-b[1]*c[1])/r;
	if ((fabs(b[0])<e1)&&(fabs(b[1])<e1))
	 goto tt;
	v=v+1;
	p=p1;
	q=q1;
	 }
	while (v<=40);
	if(v>40)
	 {
	printf("Khong hoi tu sau 40 lan lap");
	getch();
	exit(1);
	 }
	tt:s=p1/2;
	t=p1*p1+4*q1;
	if(t<0)
	 {
	printf("Nghiem phuc\n");
	printf("%.8f+%.8fj\n",s,(sqrt(-t)/2));
	printf("%.8f-%.8fj\n",s,(sqrt(-t)/2));
	printf("\n");
	 }
	else
	 {
	printf("Nghiem thuc\n");
	printf("%.8f\n",(s+sqrt(t)/2));
	printf("%.8f\n",(s-sqrt(t)/2));
	printf("\n");
	 }
	for (i=2;i<=n;i++)
	 a[i-2]=b[i];
	 n=n-2;
	 }
	while ((n>2)&(r!=0.0));
	s=-a[1]/(2*a[2]);
	t=a[1]*a[1]-4*a[2]*a[0];
	if (t<0)
	 {
	printf("Nghiem phuc\n");
	printf("%.8f+%.8fj\n",s,(sqrt(-t)/(2*a[2])));
	printf("%.8f-%.8fj\n",s,(sqrt(-t)/(2*a[2])));
	printf("\n");
	 }
	else
	 {
	printf("Nghiem thuc\n");
	printf("%.8f\n",(s-sqrt(t)/(2*a[2])));
	printf("%.8f\n",(s-sqrt(t)/(2*a[2])));
	printf("\n");
	 }
	getch();
 }
	Dùng chương trình trên để xác định nghiệm của đa thức :
	x6 - 2x5 - 4x4 + 13x3 - 24x2 + 18x - 4 = 0
ta nhận được các nghiệm :
	x1 = 2.61903399
	x2 = -2.73205081
	x3 = 0.732050755
	x4 = 0.381966055
	x5 = 0.500011056 + i*1.3228881
	x6 = 0.500011056 - i*1.3228881
§11. HỆ PHƯƠNG TRÌNH PHI TUYẾN
	Phương pháp Newton có thể được tổng quát hoá để giải hệ phương trình phi tuyến dạng :
hay viết gọn hơn dưới dạng :
	F(X) = 0
Trong đó : 	
X = (x1,x2,x3,.....,xn)
	Với một phương trình một biến, công thức Newton là :
hay :	f'(xi).Dx = -f(xi)
với	Dx = xi+1 - xi
Đối với hệ,công thức lặp là :
 J(Xi)Dx = -F(Xi)
Trong đó J(Xi) là toán tử Jacobi. Nó là một ma trận bậc n ( n - tương ứng với số thành phần trong vectơ X) có dạng :
và	DX = Xi+1 - Xi
	Phương pháp Newton tuyến tính hoá hệ và như vậy với mỗi bước lặp cần giải một hệ phương trình tuyến tính (mà biến là Dxi) xác định bởi công thức lặp cho tới khi vectơ X(x1,x2,x3,.....,xn) gần với nghiệm.
	Dưới đây là chương trình giải hệ phương trình phi tuyến 
Ma trận đạo hàm riêng J(Xi) là :
	Ma trận này được chương trình đọc vào nhờ thủ tục doc.Trong thủ tục này,các hệ số a[i,5] là các hàm fi(x).Vectơ nghiệm ban đầu được chọn là { 0,-1,-1,1}T.Kết quả tính cho ta : x = {0.01328676,-1.94647929,-1.12499779,8.05819031 }T với độ chính xác 0.000001.Vectơ số dư r = { 0.00000536,-0.00000011,-0.00000001,-0.00000006}T.
Chương trình 2-11
//giai he pt phi tuyen
#include 
#include 
#include 
#include 
#define n 4
float a[n+1][n+2];
float x[n+1],y[n+1];
int i,j,k,l,z,r;
float e,s,t;
void main()
 {
	void doc();
 clrscr();
	printf("Cho cac gia tri nghiem ban dau\n");
	for (i=1;i<=n;i++)
	 {
	printf("x[%d] = ",i);
	scanf("%f",&x[i]);
	 }
	e=1e-6;
	z=30;
	for (r=1;r<=z;r++)
	 {
	doc();
	for (k=1;k<=n-1;k++)
	 {
	s=0 ;
	for (i=k;i<=n;i++)
	 {
	t=fabs(a[i][k]);
	if (s<=t)
	 {
	s=t;
	l=i;
	 }
	 }
	for (j=k;j<=n+1;j++)
	 {
	s=a[k][j];
	a[k][j]=a[l][j];
	a[l][j]=s;
	 }
	if (a[1][1]==0)
	 {
	printf("Cac phan tu duong cheo cua ma tran bang khong");
	getch();
	exit(1);
	 }
	else
	 {
	if (fabs(a[k][k]/a[1][1])<(1e-08))
	 {
	printf("Ma tran suy bien");
	goto mot;
	 }
	 }
	for (i=k+1;i<=n;i++)
	 {
	if (a[k][k]==0)
	 {
	printf("Cac phan tu duong cheo cua ma tran bang khong\n");
	goto mot;
	 }
	s=a[i][k]/a[k][k];
	a[i][k]=0;
	for (j=k+1;j<=n+1;j++)
	 a[i][j]=a[i][j]-s*a[k][j];
	 }
	y[n]=a[n][n+1]/a[n][n];
	for (i=n-1;i>=1;i--)
	 {
	s=a[i][n+1];
	for (j=i+1;j<=n;j++)
	 s=s-a[i][j]*y[j];
	if (a[i][i]==0)
	 {
	printf("Cac phan tu duong cheo cua ma tran bang khong\n");
	goto mot;
	 }
	y[i]=s/a[i][i];
	 }
	 }
	if (r!=1)
	 for (i=1;i<=n;i++)
	{
	 if (fabs(y[i])<e*fabs(x[i]))
	goto ba;
	}
	for (i=1;i<=n;i++)
	 x[i]=x[i]-y[i];
	printf("\n");
	 }
	printf("Khong hoi tu sau %d lan lap\n",z);
	goto mot;
	clrscr();
	ba:printf("Vec to nghiem\n");
	for (i=1;i<=n;i++)
	 printf("%.5f\n",(x[i]-y[i]));
	printf("\n");
	printf("Do chinh xac cua nghiem la %.5f: \n", e);
	printf("\n");
	printf("Vec to tri so du :\n");
	for (i=1;i<=n;i++)
	 printf("%.5f\n",(a[i][n+1]));
	mot:printf("\n");
	getch();
 }
void doc()
 {
	a[1][1]=3*x[1]*x[1]-3*x[2]*x[4];
	a[1][2]=-3*x[2]*x[2]-3*x[1]*x[4];
	a[1][3]=0;
	a[1][4]=-3*x[1]*x[2];
	a[1][5]=x[1]*x[1]*x[1]-x[2]*x[2]*x[2]-3*x[1]*x[2]*x[4]-8;
	a[2][1]=1;
	a[2][2]=1;
	a[2][3]=1;
	a[2][4]=1;
	a[2][5]=x[1]+x[2]+x[3]+x[4]-5;
	a[3][1]=-x[1]/sqrt(25-x[1]*x[1]);
	a[3][2]=0;
	a[3][3]=8;
	a[3][4]=0;
	a[3][5]=sqrt(25-x[1]*x[1])+8*x[3]+4;
	a[4][1]=2*x[2]*x[3];
	a[4][2]=2*x[1]*x[3];
	a[4][3]=2*x[1]*x[2];
	a[4][4]=-1;
	a[4][5]=2*x[1]*x[2]*x[3]-x[4]+8;
 }