Bài giảng Toán rời rạc - Chương: Đồ thị - Trần Vĩnh Đức
Đồ thị Hollywood
▶ Đỉnh: các diễn viên
▶ Diễn viên a nối với diễn viên b nếu
a và b đóng chung một bộ phim
▶ Số Bacon của diễn viên c là đường
đi ngắn nhất giữa c và Kevin
Bacon.
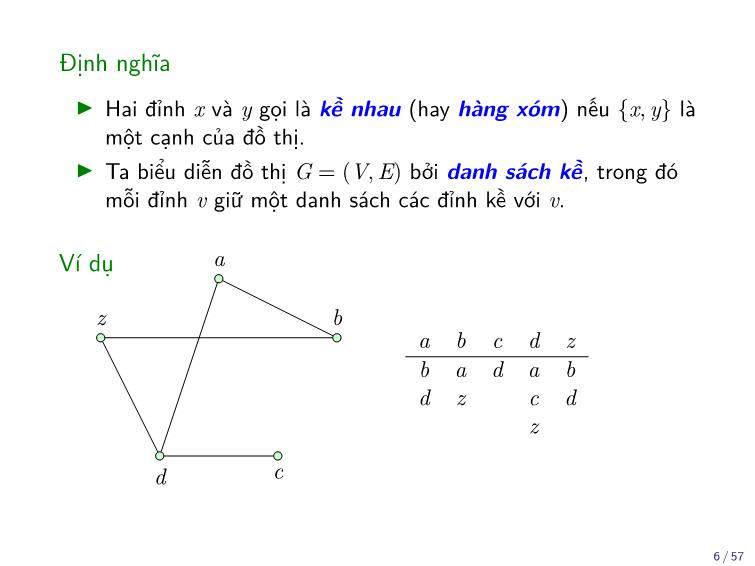
Định nghĩa
Ta ký hiệu x ∼ y nếu hai đỉnh x và y trong G có thể nối với nhau
bằng một đường đi. Có nghĩa rằng, tồn tại một đường đi
v1; v2; · · · ; vk
trong G với x = v1 và y = vk.

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương: Đồ thị - Trần Vĩnh Đức", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương: Đồ thị - Trần Vĩnh Đức

vertex
set partitioned into two subsets of m and n vertices, respectively with an edge between two
vertices if and only if one vertex is in the first subset and the other vertex is in the second subset.
The complete bipartite graphs K2,3, K3,3, K3,5, and K2,6 are displayed in Figure 9. ▲
K2,3 K3,3
K3,5 K2,6
FIGURE 9 Some Complete Bipartite Graphs.
Bipartite Graphs and Matchings
Bipartite graphs can be used to model many types of applications that involve matching the
elements of one set to elements of another, as Example 14 illustrates.
EXAMPLE 14 Job Assignments Suppose that there are m employees in a group and n different jobs that
need to be done, where m n. Each employee is trained to do one or more of these n jobs. We
would like to assign an employee≥ to each job. To help with this task, we can use a graph to model
employee capabilities. We represent each employee by a vertex and each job by a vertex. For
each employee, we include an edge from that employee to all jobs that the employee has been 22 / 57
trained to do. Note that the vertex set of this graph can be partitioned into two disjoint sets, the
set of employees and the set of jobs, and each edge connects an employee to a job. Consequently,
this graph is bipartite, where the bipartition is (E, J ) where E is the set of employees and J is
the set of jobs. We now consider two different scenarios.
First, suppose that a group has four employees: Alvarez, Berkowitz, Chen, and Davis;
and suppose that four jobs need to be done to complete Project 1: requirements, architecture,
implementation, and testing. Suppose that Alvarez has been trained to do requirements and
testing; Berkowitz has been trained to do architecture, implementation, and testing; Chen has
been trained to do requirements, architecture, and implementation; and Davis has only been
trained to do requirements. We model these employee capabilities using the bipartite graph in
Figure 10(a).
Second, suppose that a group has second group also has four employees: Washington, Xuan,
Ybarra, and Ziegler; and suppose that the same four jobs need to be done to complete Project 2 as
are needed to complete Project 1. Suppose that Washington has been trained to do architecture;
Xuan has been trained to do requirements, implementation, and testing;Ybarra has been trained
to do architecture; and Ziegler has been trained to do requirements, architecture and testing. We
model these employee capabilities using the bipartite graph in Figure 10(b).
To complete Project 1, we must assign an employee to each job so that every job has an
employee assigned to it, and so that no employee is assigned more than one job. We can do this
by assigning Alvarez to testing, Berkowitz to implementation, Chen to architecture, and Davis
to requirements, as shown in Figure 10(a) (where blue lines show this assignment of jobs).
To complete Project 2, we must also assign an employee to each job so that every job has
an employee assigned to it and no employee is assigned more than one job. However, this is
Câu hỏi
Đồ thị Km,n có bao nhiêu cạnh?
23 / 57
Bài tập
Hãy xây dựng một đồ thị với 5 đỉnh và 6 cạnh mà không chứa C3
(tam giác) nào.
24 / 57
Nội dung
Đồ thị và biểu diễn
Một số đồ thị đặc biệt
Đẳng cấu
Bậc
Đường đi và chu trình
Định nghĩa
Hai đồ thị G1 và G2 được gọi là đẳng cấu nếu có một song ánh α
từ tập đỉnh của G1 đến tập đỉnh của G2 sao cho {α(x), α(y)} là
một cạnh của G1 nếu và chỉ nếu {x, y} là một cạnh của G2.
Song ánh α được gọi là một đẳng cấu.
26 / 57
Ví dụ
Hai đồ thị sau đây đẳng cấu với nhau và đẳng cấu α định nghĩa
bởi:
α(a) = t, α(b) = v, α(c) = w, α(d) = u.
a b t
w
d c v u
27 / 57
Ví dụ
Hai đồ thị sau có đẳng cấu không?
a a
e b e b
d c d c
28 / 57
Bài tập
Hãy chứng minh rằng hai đồ thị sau không đẳng cấu.
29 / 57
Nội dung
Đồ thị và biểu diễn
Một số đồ thị đặc biệt
Đẳng cấu
Bậc
Đường đi và chu trình
Định nghĩa
Bậc của một đỉnh v trong đồ thị G = (V, E) là số cạnh của G
chứa v. Ta ký hiệu deg(v) là bậc của đỉnh v. Có nghĩa rằng
deg(v) = |Dv| với Dv = {e ∈ E | v ∈ e }.
Ví dụ a
z b đỉnh deg
a 2
b 2
c 1
d 3
z 2
d c
31 / 57
Định lý
Tổng các bậc deg(v), lấy trên mọi đỉnh v của đồ thị G = (V, E),
bằng hai lần số cạnh:
∑
deg(v) = 2|E|.
v∈V
Ví dụ
a
đỉnh thuộc vào cạnh
z b
a {a, b}, {a, d}
b {a, b}, {b, z}
c {c, d}
d {a, d}, {c, d}, {d, z}
z {b, z}, {d, z}
d c
32 / 57
Một đỉnh của đồ thị G là lẻ nếu bậc của nó là lẻ, và là chẵn nếu
bậc của nó là chẵn.
Hệ quả
Số đỉnh lẻ của đồ thị là số chẵn.
Chứng minh.
∑ ∑
deg(v) + deg(v) = 2|E|
∈ ∈
v Vlẻ v Vchẵn
33 / 57
Bậc và đẳng cấu
▶
Nếu α : V1 → V2 là một đẳng cấu giữa G1 và G2 và
α(v) = w, vậy
deg(v) = deg(w).
Tại sao?
▶
Nếu trong G1 có đỉnh x với deg(x) = δ0 và trong G2 không có
đỉnh nào có bậc δ0, vậy thì G1 và G2 không đẳng cấu.
34 / 57
Bài tập
Các dãy số sau đây có thể là các bậc của mọi đỉnh của đồ thị nào
đó không? Nếu có hãy vẽ một đồ thị như vậy.
1. 2, 2, 2, 3 3. 2, 2, 4, 4, 4
2. 1, 2, 2, 3, 4 4. 1, 2, 3, 4.
35 / 57
Bài tập
▶ Xét đồ thị G = (V, E), phần bù G của G là đồ thị có cùng
tập đỉnh là V và tập cạnh là tất cả các cặp đỉnh phân biệt
không kề nhau trong G.
▶ Giả sử G có n đỉnh và các bậc của nó là
d1, d2,..., dn.
Các bậc của G là gì?
36 / 57
Đồ thị chính quy
▶ Đồ thị mà trong đó mọi đỉnh đều có cùng bậc r được gọi là
chính quy. Khi đó r|V| = 2|E|.
▶
Đồ thị Kn là đồ thị chính quy bậc n − 1.
▶
Đồ thị vòng Cn là đồ thị chính quy bậc 2.
▶
Đồ thị Qn là đồ thị chính quy bậc mấy ?
37 / 57
a 0
e b 4 1
d c 3 2
Hình: Đồ thị đầy đủ K5 và đồ thị chu trình C5
38 / 57
Bài tập
Liệt kê các đồ thị chính quy bậc 4 (đôi một không đẳng cấu) với
bảy đỉnh.
39 / 57
Bài tập
Chứng minh rằng trong mọi đồ thị với ít nhất hai đỉnh luôn có hai
đỉnh cùng bậc.
40 / 57
Nội dung
Đồ thị và biểu diễn
Một số đồ thị đặc biệt
Đẳng cấu
Bậc
Đường đi và chu trình
Định nghĩa
Một hành trình trong đồ thị G là một dãy đỉnh
v1, v2,..., vk,
thỏa mãn vi và vi+1 kề nhau (với 1 ≤ i ≤ k − 1).
a
e b
d c
42 / 57
Định nghĩa
Hành trình mà trong đó mọi đỉnh đều khác nhau được gọi là
đường đi.
a
e b
d c
43 / 57
10.4 Connectivity 681
TABLE 1 The Number TABLE 2 The Number
Đồ thị cộng tác of Mathematicians of Actors with a Given
with a Given Erd˝os Bacon Number (as of
Number (as of early early 2011).
2006).
Bacon Number
Erd˝os Number Number of People
Number of People
0 1
0 1 1 2,367
1 504 2 242,407
2 6,593 3 785,389
3 33,605 4 200,602
4 83,642 5 14,048
5 87,760
▶ Đỉnh: các tác giả 6 1,277
6 40,014 7 114
▶ Đỉnh a nối b nếu hai tác giả a và b 7 11,591 8 16
8 3,146
viết chung bài báo. 9 819
▶ Số Erdös của nhà toán học m là 10 244
11 68
đường đi ngắn nhất giữa m và Paul 12 23
Erdös. 13 5
game where participants where challenged to find a sequence of movies leading from each actor
named to Kevin Bacon. We can find a number similar to a Bacon number using any actor as the
center of the acting universe. L
44 / 57
Connectedness in Undirected Graphs
When does a computer network have the property that every pair of computers can share infor-
mation, if messages can be sent through one or more intermediate computers? When a graph
is used to represent this computer network, where vertices represent the computers and edges
represent the communication links, this question becomes: When is there always a path between
two vertices in the graph?
DEFINITION 3 An undirected graph is called connected if there is a path between every pair of distinct
vertices of the graph. An undirected graph that is not connected is called disconnected.We
say that we disconnect a graph when we remove vertices or edges, or both, to produce a
disconnected subgraph.
Thus, any two computers in the network can communicate if and only if the graph of this network
is connected.
EXAMPLE 4 The graph G1 in Figure 2 is connected, because for every pair of distinct vertices there is a
path between them (the reader should verify this). However, the graph G2 in Figure 2 is not
connected. For instance, there is no path in G2 between vertices a and d. L
We will need the following theorem in Chapter 11.
10.4 Connectivity 681
TABLE 1 The Number TABLE 2 The Number
Đồ thị Hollywoodof Mathematicians of Actors with a Given
with a Given Erd˝os Bacon Number (as of
Number (as of early early 2011).
2006).
Bacon Number
Erd˝os Number Number of People
Number of People
0 1
0 1 1 2,367
1 504 2 242,407
2 6,593 3 785,389
▶ Đỉnh: các3 diễn viên33,605 4 200,602
▶ Diễn viên4 a nối với83,642 diễn viên b nếu 5 14,048
5 87,760
a và b đóng chung một bộ phim 6 1,277
6 40,014 7 114
▶
Số Bacon7 của diễn11,591 viên c là đường 8 16
đi ngắn nhất8 giữa 3,146c và Kevin
Bacon. 9 819
10 244
11 68
12 23
13 5
45 / 57
game where participants where challenged to find a sequence of movies leading from each actor
named to Kevin Bacon. We can find a number similar to a Bacon number using any actor as the
center of the acting universe. L
Connectedness in Undirected Graphs
When does a computer network have the property that every pair of computers can share infor-
mation, if messages can be sent through one or more intermediate computers? When a graph
is used to represent this computer network, where vertices represent the computers and edges
represent the communication links, this question becomes: When is there always a path between
two vertices in the graph?
DEFINITION 3 An undirected graph is called connected if there is a path between every pair of distinct
vertices of the graph. An undirected graph that is not connected is called disconnected.We
say that we disconnect a graph when we remove vertices or edges, or both, to produce a
disconnected subgraph.
Thus, any two computers in the network can communicate if and only if the graph of this network
is connected.
EXAMPLE 4 The graph G1 in Figure 2 is connected, because for every pair of distinct vertices there is a
path between them (the reader should verify this). However, the graph G2 in Figure 2 is not
connected. For instance, there is no path in G2 between vertices a and d. L
We will need the following theorem in Chapter 11.
Định nghĩa
Ta ký hiệu x ∼ y nếu hai đỉnh x và y trong G có thể nối với nhau
bằng một đường đi. Có nghĩa rằng, tồn tại một đường đi
v1, v2, ··· , vk
trong G với x = v1 và y = vk.
a
e b
d c
46 / 57
Dễ thấy, quan hệ ∼ là quan hệ tương đương trên tập đỉnh V của G.
Vậy thì V được phân hoạch thành các lớp tương đương rời nhau.
Hai đỉnh nằm trong cùng một lớp nếu giữa chúng có đường đi, và
trong hai lớp khác nhau nếu không có đường đi.
Ví dụ
a
Với đồ thị bên, ta có phân hoạch: f b
V = Vđỏ ∪ Vxanh e c
d
47 / 57
Định nghĩa
Giả sử G = (V, E) là một đồ thị và phân hoạch của V tương ứng
với quan hệ tương đương ∼ là
V = V1 ∪ V2 ∪ · · · ∪ Vr.
Ký hiệu Ei (với 1 ≤ i ≤ r) là các tập con của E bao gồm các cạnh
với đầu mút nằm trong Vi. Vậy thì các đồ thị Gi = (Vi, Ei) được
gọi là các thành phần liên thông của G.
Ta nói G liên thông nếu nó chỉ có một thành phần liên thông.
48 / 57
Ví dụ
Đồ thị dưới đây không liên thông. Nó có hai thành phần liên thông.
a
f b
e c
d
49 / 57
Bài tập
Tìm số thành phần liên thông của đồ thị với danh sách kề là
a b c d e f g h i j
f c b h c a b d a a
i g e g i c f f
j g j e
50 / 57
Bài tập
Đồ thị mô tả bữa tiệc của bà April có bao nhiêu thành phần liên
thông?
51 / 57
Định nghĩa
Một hành trình
v1, v2, ··· , vr+1
trong đó mọi đỉnh đều phân biệt ngoại trừ v1 = vr+1 được gọi là
một chu trình.
Vì nó có r đỉnh phân biệt và r cạnh nên ta cũng thường gọi nó là
r-chu trình, hay chu trình độ dài r.
a
e b
d c
52 / 57
Bài tập
▶ Hình dưới đây thể hiện các địa điểm thú vị trên đảo Wanda và
đường đi giữa chúng.
▶ Hãy tìm đường đi trên đảo để thăm mỗi địa điểm đúng một
lần và trở về vị trí xuất phát.
p q
s
r t
u
53 / 57
Bài tập
Hãy tìm cách để đi hết các con đường, mỗi đường đúng một lần.
Địa điểm bắt đầu và kết thúc có thể khác nhau.
p q
s
r t
u
54 / 57
Định nghĩa
▶ Chu trình chứa mọi đỉnh của đồ thị gọi là chu trình
Hamilton.
▶ Hành trình dùng mỗi cạnh đúng một lần gọi là hành trình
Euler.
55 / 57
Bài tập
Tìm chu trình Hamilton của đồ thị tạo bởi các đỉnh và cạnh của 10.7 Planar Graphs 719
khối lập phương.
FIGURE 2 The FIGURE 3 K4 Drawn FIGURE 4 The FIGURE 5 A Planar
Graph K4. with No Crossings. Graph Q3. Representation of Q3.
56 / 57
DEFINITION 1 A graph is called planar if it can be drawn in the plane without any edges crossing (where
a crossing of edges is the intersection of the lines or arcs representing them at a point other
than their common endpoint). Such a drawing is called a planar representation of the graph.
A graph may be planar even if it is usually drawn with crossings, because it may be possible
to draw it in a different way without crossings.
EXAMPLE 1 Is K4 (shown in Figure 2 with two edges crossing) planar?
Solution: K4 is planar because it can be drawn without crossings, as shown in Figure 3. L
EXAMPLE 2 Is Q3, shown in Figure 4, planar?
Solution: Q3 is planar, because it can be drawn without any edges crossing, as shown in
Figure 5. L
We can show that a graph is planar by displaying a planar representation. It is harder to
show that a graph is nonplanar. We will give an example to show how this can be done in an ad
hoc fashion. Later we will develop some general results that can be used to do this.
EXAMPLE 3 Is K3,3, shown in Figure 6, planar?
Solution: Any attempt to draw K3,3 in the plane with no edges crossing is doomed. We now
show why. In any planar representation of K3,3, the vertices v1 and v2 must be connected to both
v4 and v5. These four edges form a closed curve that splits the plane into two regions, R1 and
R2, as shown in Figure 7(a). The vertex v3 is in either R1 or R2. When v3 is in R2, the inside
of the closed curve, the edges between v3 and v4 and between v3 and v5 separate R2 into two
subregions, R21 and R22, as shown in Figure 7(b).
v1 v5 v1 v5
v 1 v 2 v 3
R21
R 2 R 1 v3 R 1
R22
v4 v2 v4 v2
v 4 v 5 v 6 (a) (b)
FIGURE 6 The Graph K3,3. FIGURE 7 Showing that K3,3 Is Nonplanar.
Bài tập
Năm tới, Dr Chunner và Dr Dodder định đi thăm đảo Mianda. Các
địa điểm hấp dẫn và đường đi nối giữa chúng được biểu diễn bởi
đồ thị có danh sách kề là
0 1 2 3 4 5 6 7 8
1 0 1 0 3 0 1 0 1
3 2 3 2 5 4 5 2 3
5 6 7 4 6 7 6 5
7 8 8 8 8 7
▶ Liệu họ có thể tìm đường đi trên đảo để thăm mỗi địa điểm
đúng một lần và trở về vị trí xuất phát?
▶ Liệu họ có thể tìm cách để đi hết các con đường, mỗi đường
đúng một lần; địa điểm bắt đầu và kết thúc có thể khác nhau?
57 / 57File đính kèm:
 bai_giang_toan_roi_rac_chuong_do_thi_tran_vinh_duc.pdf
bai_giang_toan_roi_rac_chuong_do_thi_tran_vinh_duc.pdf

