Bài giảng Nguyên lý máy - Chương II: Phân tích động học cơ cấu

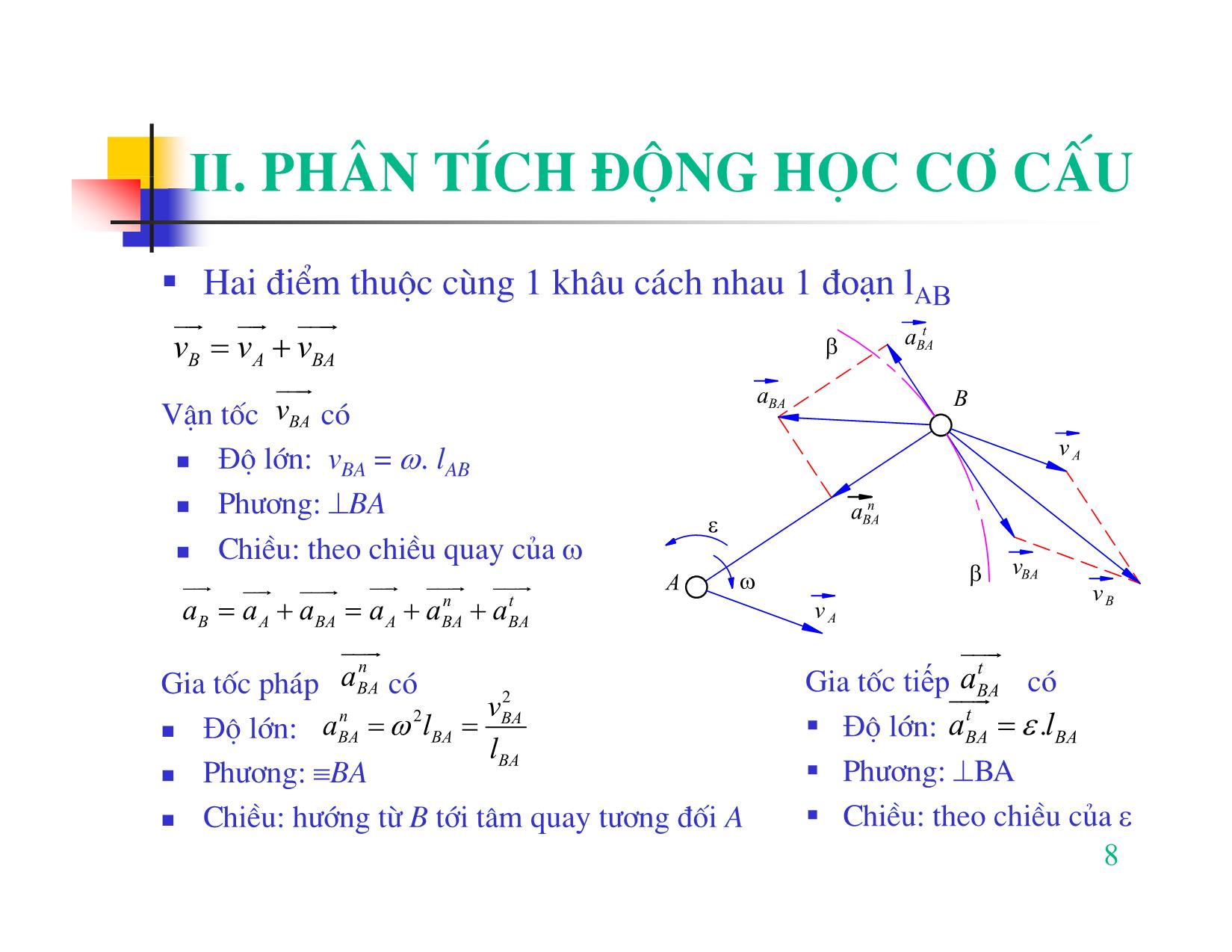
ột đoạn bằng chiều dμi
 thanh truyền BC, một mặt phải nằm trên quỹ đạo của C khi quay
 quanh D. Vậy ta lấy C lμ giao điểm của vòng tròn (D, CD) vμ vòng
 y
 tròn (B, BC). C
 B 2
ƒ Bμi toán quỹ đạo: 1 3
 ϕ1
Đểgiảibμitoánnμy, ta chỉ cần xác định A D
 x
 4 4
một loạt hoạ đồ vị trí nối tiếp nhau trong C'
phạm vi 1 chu kỳ động học của cơ cấu
 II. Phân tích động học cơ cấu
2.3. Các ph−ơng trỡnh cơ bản xác địịậnh vận tốc vμ 
gia tốc
 ƒ Khâu chuyygển động tịnh tiến
 „ Vận tốc góc ω của khâu bằng 0.
 „ Tất cả các điểm của khâu đều có cùng vận tốc vμ gia tốc:
 a C
 a
 vvvABC===... B
 aaa===... a
 ABC A C
 vC
 B
 v
 A B
 6
 v A
 II. Phân tích động học cơ cấu
 t
 a A
 a
ƒ Khâu quay quanh trục cố định A A
 Vận tốc của điểm A có α
 „ Độ lớn: vl= ω. n
 A OA a A
 ε v A
 „ Ph−ơng: ⊥ OA
 O ω
 „ Chiều: theo chiều quay của ω
 Gia tốc pháp của điểm A có
 2 Gia tốc tiếp của điểm A có
 n2 vA
 „ Độ lớn: a = ω .l =
 A OA ƒ alt = ε.
 lOA Độ lớn A OA
 „ Ph−ơng: ≡ OA ƒ Ph−ơng: ⊥ OA
 „ Chiều: h−ớng từ A tới tâm quay O ƒ Chiều: theo chiều của ε
 uur u urnt u ur
 Gia tốc toμn phần của điểm A aaaA = AA+ có
 42
 ƒ Độ lớn: alAOA= ω + ε t
 uur aA ε ⎛⎞ε
 ƒ aA hợp với OA một góc α có: tgαα==→=n 22 arctg ⎜⎟
 aA ω ⎝⎠ω
 7
 II. Phân tích động học cơ cấu
ƒ Haiđiểmthuộccùng 1 khâu cách nhau 1 đoạnlAB
 uuruuruuur t
 β aBA
 vvvBABA=+
 uuur aBA B
Vận tốc vBA có
 v A
 „ Độ lớn: vBA = ω. lAB
 „ Ph−ơng: ⊥BA a n
 ε BA
 „ Chiều: theo chiều quay của ω
 v
 A ω β BA
 uuruur uuur uur uuuntruuur v B
 aaaB =+A BA =+ aa A BA + a BA v A
 uuunr uuut r
Gia tốc phápaBA có Gia tốc tiếp aBA có
 2 uuur
 n 2 vBA t
„ Độ lớn: alBA==ω BA ƒ Độ lớn: alBABA= ε.
 lBA
„ Ph−ơng: ≡BA ƒ Ph−ơng: ⊥BA
„ Chiều: h−ớng từ B tới tâm quay t−ơng đối A ƒ Chiều: theo chiều của ε
 8
 II. Phân tích động học cơ cấu
„ Quan hệ vận tốc, gia tốc 2 điểm thuộc 2 khâu tạo thμnh khớp
 tr−ợt vμ trùng nhau tức thời
 Xét 2 điểm B1 vμ B2 thuộc 2 khâu tạo thμnh khớp tr−ợt trùng nhau tức thời tại
 thời điểm đang xét. Chuyển động của B2 gồm 2 chuyển động: chuyển động theo
 cùng với B1 vμ chuyển động t−ơng đối đối với B1
 ω1 =ω2 x
 Vận tốc điểm B2 đ−ợc xác định nh− sau:
 vBBB B
 uur uur uuuur B 21
 vvv=+ 2
 BBBB2121 2
 uuuur
 B1 ε = ε
 Vận tốc t−ơng đốiv song song với ph−ơng tr−ợt 1 2
 B21B 1
 x a k
 B 2 B 1
 a k
 B 2 B 1
 9
 II. Phân tích động học cơ cấu
„ Quan hệ vận tốc, gia tốc 2 điểm thuộc 2 khâu tạo thμnh khớp
 tr−ợt vμ trùng nhau tức thời
 x
 Gia tốc điểm B2 đ−ợc xác định nh− sau: ω1 =ω2
 uuur uur uuuurrk uuuur
 aaa=+ + a vB B
 B2 B 1 BB 21 BB 21 B 21
 uuuur 2
 Gia tốc t−ơng đốiar song song với ph−ơng tr−ợt 2
 B21B
 uuuur B1 ε = ε
 ak 1 2
 Gia tốc Côriôlit B21B có 1
 x a k
 k B 2 B 1
 „ Độ lớn: aB B = 2ω1vB B
 2 1 2 1 a k
 B 2 B 1
 „ Ph−ơng: ⊥ ω vμ 
 1 uuuur
 „ v 0
 Chiều: cùng ph−ơng chiều vớiBB21 quay đi 90 theo chiều quay của ω1
 10
 II. Phân tích động học cơ cấu
2.4. Phân tích độộgng họcbằng ph−ơng pppháp đồ giải
 2.4.1 Bμi toán vị trí
 N
 ộ
 ộ
 2.4.2 Bμi toán vận tốc
 i d
 u
 ng 2432.4.3 Bμi toán gia tốc 
 2.4.4 Một số ví dụ khác
 11
 II. Phân tích động học cơ cấu
2.4.1 Bμi toán vị trí
 Khi cơ cấu chuyển động, vị trí của các khâu luôn thay đổi nh−ng ở mỗi thời điểm, 
 vị trí của chúng hoμn toμn xác định 
 Xét cơ cấu 4 khâu bản lề phẳng (loại 2) 
 C
 B 2
 1 3
 ϕ1
 A D
 4 4
 12
 II. Phân tích động học cơ cấu
2.4.1 Bμi toán vị trí
 B−ớc 1: Chọn tỷ lệ xích hoạ đồ 
 y
 C
 B 2 lXY ⎛⎞m
 μl = ⎜⎟
 XYmm⎝⎠
 1 3
 ϕ
 1 Trong đó:
 A D
 lXY lμ chiều dμithực
 x
 của đoạn XY (m),
 4 4
 C' XY lμ chiều dμi biểu thị trên
 hoạ đồ cơ cấu (mm)
 B−ớc 2: Vẽ giá AD vμ quỹ đạo điểm B
 Điểm C do cách dựng hỡnh nên có 2 vị trí. trên khâu dẫn AB
 Đểtỡm vị trí thực của nó, ta phải dựa vμo
 tính liên tục khi chuyển động của các khâu B−ớc 3: C lμ giao điểm của vòng tròn 
 trong cơ cấu (D, CD) vμ vòng tròn (B, BC) 
 13
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán vận tốc
 Xác định vận tốc của C, E trên khâu 2 vμ ω2, ω3, trong 
 cơ cấu 4 khâu b ản lề phẳng 
 E
 2 C uur
 B Tỡm vB
 F Do B quay quanh điểm cố định A nên 
 1 3
 Độlớnộ lớn vlBAB= ω1.
 A D Ph−ơng: ⊥ AB
 ω1
 Chiều: theo chiều quay của ω1
 4 4
 14
 II. Phân tích động học cơ cấu
 2.4.2 Bμi toán vận tốc
 Dựng hoạ đồ vận tốc với 
 −1
 E vB ⎛⎞ms.
 μv = ⎜⎟
 2 C pbmm⎝⎠
 B Viết lại hệ pt trên d−ới dạng các 
 F
 c
 p=d
 1 3 vector biểu diễn 
 e uur uur uur
A D f pcpbbc=+
 ω1
 (⊥ AB,.ω1 lAB ) (⊥ BC ,?)
 b
 4 4 uur uuuruur
 uur pc=+ pd dc
 Tim vC r
 (0?0) (⊥ CD, ?)
 Xét điểm C có quan hệ với điểm B vμ D
 uuruuruuur Từ hoạ đồ vừa dựng ta đ−ợc: 
 vvCB=+ v CB uuruur
 vpcCv= μ .
 (⊥⊥AB,.ω1 lAB ) ( BC ,?) uuuruur
 uuruur uuur vbcCB= μ v .
 vvCD=+ v CD
 r 15
 ()0,?()⊥ CD
 II. Phân tích động học cơ cấu
 2.4.2 Bμi toán vận tốc
 uur
 Tỡm vE
 E uuruuruuur
 vvEB=+ v EB
 2 C
 B
 (⊥⊥AB,.ω1 lAB ) ( BE ,?)
 F
 c uuruur uuur
 3 p=d
 1 e vvEC=+ v EC
A D f ⊥⊥CD,.μ pc CE ,?
 ω1 ()()v
 Viết lại hệ pt trên d−ới dạng các 
 b
 4 4 vector biểu diễn 
 uur uur uur
 pepbbe=+
 (⊥ ABl,.ω1 AB ) (⊥ BE ,?)
 uur uur uur
 pepcce=+
 (⊥⊥CD,.μv pc) ( CE ,?)
 Từ hoạ đồ vừa dựng ta đ−ợc:
 uuruur
 vpeEv= μ . 16
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán vận tốc
Từ hoạ đồ vận tốc trên ta có đ−ợc các kết luận sau:
 Vậntốccógốc tại p vμ mút tạicác
 điểm b, c,.. đều biểu thị vận tốc tuyệt
 đối của các điểm B, C,..trêncơcấu. E
 2 C
 B
 Cực p biểu thị các điểm có vận tốc F
 c
 bằng 0 trên hoạ đồ vị trí. 3 p=d
 1 e
 A D f
 Vận tốc không có gốc tại p biểu thị ω1
 vận tốc t−ơng đối giữa các điểm (chú
 uuur b
 uur 4 4
 ý cách viết:bc t−ơng ứng vớivCB )
 17
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán vận tốc
Định lý đồng dạng thuận:
Hinh nối các ngọn vector biểu thỡ vận tốc
tuyệt đối của các điểm thuộc cùng một khâu
của hoạ đồ vận tốc đồng dạng thậhuận với hỡnh E
nối các điểm cùng tên t−ơng ứng trên hoạ đồ 2 C
 B
vị trí F
 c
 3 p=d
Nếu biết 2 điểm thuộ ccùng 1 khâu thỡ vận 1 e
tốc của điểm thứ 3 trên khâu đó bao giờ cũng A D f
 ω1
xác định đ−ợc nhờ định lý nμy
 b
 4 4
VD. 
Xác định vận tốc của điểm F trên đoạn BC: 
 18
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán vận tốc
 uur uur
Tỡm ω23, ω
Từ hoạ đồ vân tốc ta có thể xác định đ−ợc: 
 E
uur 2 C
ω2 B
 vbcμ . F
 CB v c
 Độ lớn: ω2 ==
 3 ppd=d
 llCB CB 1 e
 uuur
 Chiều theo chiều của v A D f
 CB ω1
uur
ω b
 3 4 4
 vdcCDμ v
 Độ lớn: ω3 ==
 llCD CD
 uuur
 Chiều theo chiều của vCD
 19
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán GIA tốc
 Xác định gia tốc của C, E trên khâu 2 vμ ε 2, ε 3, trong
 cơ cấu 4 khâu bản lề phẳng 
 E
 2 C uur
 B Tỡm aB
 F Do B quay quanh điểm cố định A nên 
 3
 1 uur uurnt uur
 aaaBBB= +
 A ω D n 2
 1 alBAB= ω1 . h−ớng từ B tới A, 
 uurt r
 4 4 aB = 0 do khâu AB quay đều 
 20
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán GIA tốc
 E
 uur π=d
 Tim a
 C 2 C
 B
 F
 1 3
 nCD
 A ω D c
 1 n
 EC f
 e
 4 4
 nCB b
 nEB
 Xét điểm C có các quan hệ với các điểm B vμ D
 uur u ur u unt uruuur
 aaC=++ B a CB a CB
 22
 ()()AB,.ωω12 lAB CB ,. l CB ()⊥ CB ,?
 uur uur uuurnt uuur
 aaC=+ D a CD + a CD
 r 2
 ()0,.,?()CDω3 lCD ()⊥ CD 21
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán GIA tốcE
 uur π=d
Tỡm aC
 2 C
 Dựng hoạ đồ vận tốc với B
 a F
 μ = B
 a πb 1 3
 nCD
 A ω D c
 1 n
 EC f
 e
 4 4
 nCB b
 nEB
 Viết lại hệ pt trên d−ới dạng các vector biểu diễn Từ hoạ đồ vừa dựng, ta đ−ợc: 
 uur uur uuuur uuuur
 acCa= μ .π
 ππcb=++ bnncCB CB
 22
 ()()AB,.ωω12 lAB CB ,. l CB ()⊥ CB ,?
 uur uuur uuuur uuuur
 πcd=+π dnCD + nc CD
 r
 0,.,?CDω 2 l⊥ CD
 () () 3 CD () 22
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán GIA tốc
 E
Tỡm ε2, ε3 π=d
 2 C
 B
 F
 1 3
 nCD
 A ω D c
 1 n
 EC f
 e
 4 4
 nCB b
 nEB
 t
 t
 ancCB CB.μ a
 ancCD CD.μ a
 ε 2 ==
 ε3 ==
 llCB CB
 llCD Cd
 uuut r
 uuurt
 đặt a CB tạ i điể m C ta sẽ cóđó đ−ợc 
 đặt a CD tại điểm C ta sẽ có đ−ợc 
 chiều của εr r
 2 chiều của ε3
 23
 II. Phân tích động học cơ cấu
2.4.2uur Bμi toán GIA tốc
 Tỡm a E
 E π=d
 2 C
 B
 F
 1 3
 nCD
 A ω D c
 1 n
 EC f
 e
 4 4
 nCB b
 Xét điểm E có các quan hệ với các điểm B vμ C nEB
 uur uur uuuntr uuur uur uur uuurnt uuur
 aaE=++ B a EB a EB aaE=++ C a EC a EC
 2 2
 2 ⎛⎞vEB uur ⎛⎞vEC
 (AB,.ω1 lAB ) ⎜⎟ EB ,(⊥ EB ,?) (πμπc,.a c) ⎜⎟ EC ,(⊥ EC ,?)
 ⎝⎠lEB ⎝⎠lEC
 24
 II. Phân tích động học cơ cấu
2.4.2uur Bμi toán GIA tốc
 Tỡm aE E
 π=d
 2 C
 B
 F
 1 3
 nCD
 A ω D c
 1 n
 EC f
 e
 4 4
 nCB b
 n
 ViếtlạihệpttrêndViết lại hệ pt trên d−ới dạng các vector biểu diễn EB
 uur uur uuuur uuuur uur u ur uuuur uuuur
 ππeb=++ bnneEB EB ππec=++ cnneEC EC
 2 2
 2 ⎛⎞vEB uur ⎛⎞vEC
 (AB,.ω1 lAB ) ⎜⎟ EB ,(⊥ EB ,?) (πμπc,.a c) ⎜⎟ EC ,(⊥ EC ,?)
 ⎝⎠lEB ⎝⎠lEC
 Từ hoạ đồ vừa dựng, ta đ−ợc: aeEa= μ .π
 25
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán GIA tốc
 E
 π=d
 2 C
 B
 F
 1 3
 nCD
 A ω D c
 1 n
 EC f
 e
 4 4
 nCB b
 n
 Từ hoạ đồ gia tốc ta có đ−ợc các kết luận sau: EB
 • Giatốccógốctạiπ vμ mút tại các điểm b, c,.. đều biểu thị gia tốc tuyệt đối của
 cácđiểmB,C,..trêncơcấu.
 • Cực π biểu thị các điểm có gia tốc bằng 0 trên hoạ đồ vị trí,
 • Gia tốc không có gốc tại π biểu thị gia tốc t−ơng đối giữa các điểm (chú ý cách
 uur uuur
 viết:bc t−ơng ứng vớia )
 CB 26
 II. Phân tích động học cơ cấu
2.4.2 Bμi toán GIA tốc
 E
 π=d Chứng minh
 2 C
 B
 nt22
 F aaaCB=+()() CB CB
 1 3
 22
 nCD 2
A D c =+()()llBC..ω22 BC ε
 ω1
 nEC
 f 42
 e =+l ωε
 4 4 n b BC 22
 CB T−ơng tự ta có: 
 nEB
 42
Định lý đồng dạng thuận: alEB= BE ω22+ε
Hỡnh nối các điểm thuộc cùng một khâu đồng
 al= ω 42+ε
dạng thuậ n với hỡnh nối các ngọn vector gia EC CE 22
 aEB aaEC CB 42
tốc (tuyệt đối) của các điểm đó trên hoạ đồ →===ω22 +ε
 lllBE CE BC
gia tốc be ce bc
 → ==
Nếu biết 2 điểmthuộc cùng 1 khâu thỡ vận tốc lllBE CE BC
của điểm thứ 3 trên khâu đó bao giờ cũng xác →Δbce~ Δ BCE
định đ−ợc 27
 II. Phân tích động học cơ cấu
2.4.3 Mộộụt số ví dụ khác
Xác định vận tốc và gia tốc của điểm D trên khâu 3 vμ ω3, ε3 của cơ cấu
culít. Cho tr−ớc các kích th−ớc của cơ cấu vμ ω1 = const = 1 (1/s).
 D
 uur uur
 Tỡm vv,
 2 BB12
 A B
 ω 1
4 1 Do B chuyển động tròn đối với A nên: 
 Độ lớn vvB = BAB= ω1. l
 3 12
 Ph−ơng: ⊥ AB
 Chiều: theo chiều quay của ω1
 ω = ω
4 2 3
 C
 28
 II. Phân tích động học cơ cấu
2.4.4 Mộộụt số ví dụ khác D
 uur
 Tỡm v
 B3
 2
 Xét điểm B3 có các quan hệ với A B
 ω 1
 các điểm B vμ C 4 1
 uur2 uur uuuur
 vv=+ v p =c
 BB32 BB 32
 3 // BC
 ()()⊥ ABl,,?ω1 AB CB
  b3
 uur uuruuur
 vv=+ v d
 BC33 BC
 vB B
 r 3 2
 0,?⊥ BC ω = ω
 () () 4 23
 b1 = b2
 Viết lạạệpi hệ pt trên d−ới dạạgng các C
 vector biểu diễn
 uuur uuur uuur Giảiph−ơng trỡnh theo ph−ơng pháp
 pbpbbb=+
 32 23 đồ giải ta xác định đ−ợc
 ⊥ ABl,,ω CB?
 ( 1 AB ) ( ) vpbBv= μ . 3
 uuur uur uuur 3
 pb33=+ pc cb
 r 29
 ()0,?()⊥ BC
 II. Phân tích động học cơ cấu
2.4.4 Mộộụt số ví dụ khác
 D
Tỡm ω3
 v
 B3 μv .pb3 2
 ω3 == A B
 ω 1
 llCB CB 4 1
 uur p =c
 v
 có chiều theo chiều của B3
 3 // BC
 uur b3
 Tỡm v
 D d
 vB B
 Dùng định lý đồng dạng thuận ta có: 3 2
 ω = ω
 4 2 3
 cd CD b1 = b2
 ΔΔ→=bcd~ BCD C
 cb3 CB
 ta xác định đ−ợc 
 vpdDv= μ .
 Hoặc dùng công thức: vl= ω .
 D 3 CD 30
 II. Phân tích động học cơ cấu
 2.4.4 Mộộụt số ví dụ khác
 uur uuur
Tỡm aa=
 BB12
uur uuur
aa==ω 2.l
 BB121 AB
h−ớng từ B tới A. (do B quay đều quanh A) 
 uuur
Tỡm a
 B3
Xét điểm B3 có các quan hệ với các điểm B2 vμ C
uuuruuur uuuur uuuur uuuruur uuuur uuuur
aa=+ akr + aaa=+ ant + a
 B3 B 2 BB 32 BB 32 B333 C BC BC
 uuuur r
 AB,,2,?ωω2 l⊥ v v CB 0,.,?BCω 2 l⊥ BC
 ()12AB() BB32 BB 32 ( ) ( ) ( 3 BC ) ( )
 uuuur
 Gia tốc Côriôlit ak
 BB32
 uuuur 0
 Chiều: Quay v 90 theo chiều quay của ω1
 BB32 31
 II. Phân tích động học cơ cấu
 2.4.4 Mộộụt số ví dụ khác D
 2
 A B
 ω 1
Viết lại hệ pt trên d−ới dạng các vector biểu diễn 4 1
 uuur uuur uuuruuur p =c
 ππbb=+ bkkb +
 32 2 3 // BC
 uuuur 3
 2 b
 AB,,2,?ωω l⊥ v v CB 3
 ()12AB() BB32 BB 32 ()
 uuur uur uuuur uuuuur d
 vB B
 πbc33=+π cnBC + nb BC 3 2
 ω2 = ω3
 r 2 4 b =b
 0,.,?BCω l⊥ BC 1 2
 () () 3 BC () C
 d b
 Từ hoạ đồ vừa dựng , ta xác định đ−ợc 3
 r
 aB B
 b =b 3 2
 ab= μ .π 12
 Ba3 3 π =c
 aB 
 k 2 t
 a nBC
 aB B B 3 C t
 3 2 aB C
 k 3
 BC
 // BC
 32
 II. Phân tích động học cơ cấu
 2.4.4 Mộộụt số ví dụ khác D
 2
Tỡm ε A B
 3 t ω1 1
 aBC 4
 3 p=cp =c
 ε3 =
 lBC
 uuuur 3 // BC
 t b
 đặt a BC tại điểm B ta sẽ có đ−ợc 3
 3 r
 chiều của ε d
 3 v
 B 3 B 2
 ω = ω
 4 2 3
 uur b1 =b2
Tỡm aD C
 d
Dùng địhlýđồđịnh lý đồng d ạng th thậuận t a có : b3
 a r
 B 3 B 2
 cd CD b12=b
 ΔΔ→=bcd~ BCD π =c
 cb CB aB 
 3 k 2 t
 a nBC
 aBBB B BCB 3 C t
 3 2 aB C
 ta xác định đ−ợc k 3
 BC
 ad= μ .π // BC
 Da 33
 II. Phân tích động học cơ cấu
2.5. Ph−ơng pháp giẢi tích
 Phân tích động học cơ cấu 4kbl
 C
 2
 Xét cơ cấu 4 khâu bản lề phẳng. B
 Biết kích th−ớc tất cả các khâu, 
 3
 Góc định vị ϕ1 của khâu dẫn 1, 1
 ϕ
 Vận tốc góc quay của khâu dẫn 1
 A D
 ω1 = const. 
 Xác định vị trí, vận tốc vμ gia tốc 
 củấủa các khâu thuộc cơ cấu. 4 4
 34
 II. Phân tích động học cơ cấu
2.5. Ph−ơng pháp giẢitích
 Xác định vị trí
 Ta có ph −ơng trỡnh vector 
 rr rr
 LL12+=+ LL 43(*) y
 L2 C
 Ta có thể viết ph−ơng trỡnh (*) d−ới dạng 2
 B ϕ L3
 ph−ơng trỡnh hỡnh chiếu 2
 L1
 3
 ⎧LL1122331cosϕϕϕ+−−= cos LL cos 0
 ⎨ 1
 LLsinϕϕϕ+− sin L sin = 0 ϕ
 ⎩ 112233 ϕ1 3
 A L4 D
 Giải hệ 2 ph−ơng trỡnh 2 ẩn
 x
 ta xác định đ−ợc ϕ2 vμ ϕ3
 4 4
 35
 II. Phân tích động học cơ cấu
2.5. Ph−ơng pháp giẢitích
 Xác định vận tốc
 Lấy đạo hμm hệ (1) theo thời gian, ta đ−ợc 
 ⎧−−LL11ωϕsin 1 2 ωϕ 2 sin 2 + L 33 ωϕ sin 3 = 0
 ⎨ (2)
 ⎩ LL11ωϕcos 1+−= 2 ωϕ 2 cos 2 L 33 ωϕ cos 3 0
 Hệ (2) có thể viết d−ới dạng ma trận 
 ⎡⎤−l2233sinϕϕ l sin ⎡⎤ω2 ⎡⎤l11sinϕ
 ⎢⎥.(3)⎢⎥= ω1 ⎢⎥
 ⎣⎦ll22cosϕϕ - l 33 cos⎣⎦ω3 ⎣⎦− 11 cos ϕ
 Hệ thức (3) có thể viết d−ới dạng tổng quát 
 [][]A . ω = ω1 []B
 Giải hệ 2 ph−ơng trỡỡnh 2 ẩn ta xác định đ−ợc ω2 vμ ω3
 36
 II. Phân tích động học cơ cấu
2.5. Ph−ơng pháp giẢitích
 Xác định gia tốc
 Lấy đạo hμm hệ (3) theo thời gian, ta đ−ợc 
 ⎡⎤⎡⎤−−ll2233sinϕϕ l sin⎡⎤εω22 ωϕωϕ 222333 cos l cos ⎡ ⎤⎡ω11l cosϕ 1⎤
 ⎢⎥⎢⎥..⎢⎥=− ⎢ ⎥ +⎢ ⎥
 ⎣⎦⎣⎦lll22cosϕ - l 33 cosϕωϕωϕωϕ⎣⎦εω33− 222333 sin l sin ⎣ ⎦⎣ 111 sin ⎦
 Giảihệ2 ph−ơng trỡnh 2 ẩn ta xác định đ−ợc ε2 vμ ε3
 Hệ thức (3) có thể viết d−ới dạng tổng quát 
 [][]A . ε = −[A&][ω]+ ω1 [B&]
 dA[ ] dB[ ]
 ⎡⎤A& ==, ⎡B& ⎤
 ⎣⎦ dt⎣⎦ dt
 37
 II. Phân tích động học cơ cấu
2.5. Ph−ơng pháp giẢi tích
 Phân tích động học cơ cấu tq-ct
 Cho cơ cấu tay quay con tr−ợt lệch 
 tâm với
 lAB, lBC, 
 ω1 = const vμ
 độ lệch tâm e. 
 Xác định xC, vC, aC?
 38
 II. Phân tích động học cơ cấu
 2.5. Ph−ơng pháp giẢi tích
Xác định vị trí
 Xác định vận tốc vμ gia tốc
 39