Bài giảng Nguyên lý máy - Chương 2: Phân tích động học cơ cấu phẳng - Nguyễn Chí Hưng
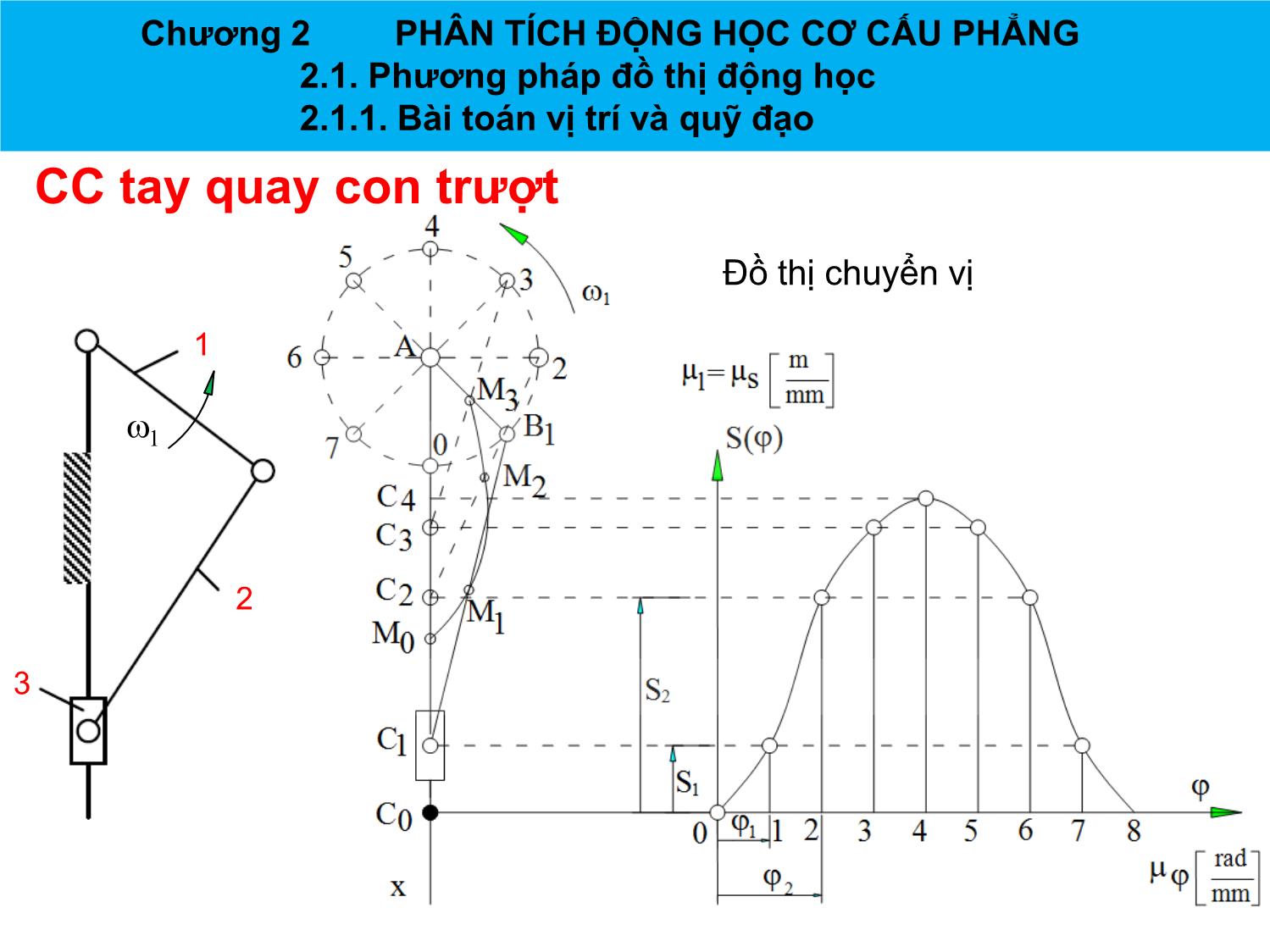
Các bước thực hiện
• Chọn tỷ xích của họa đồ là l
• Tính độ dài các đoạn biểu diễn tương ứng với kích thước các
khâu.
• Vẽ quỹ đạo của tâm khớp B thuộc khâu dẫn 1, đó là đường tròn
tâm A bán kính AB = lAB/l .
• Chia vòng tròn (A, AB) ra n phần bằng nhau bởi các điểm Bi (i = 0
n ). Trong ví dụ này, để đơn giản ta chọn n = 8.
Vẽ các vị trí ABi của tay quay.
• Gọi Ci là vị trí của con trượt 3 tương ứng với vị trí ABi của tay
quay. Ta có nhận xét:
Kích thước khâu 2 không đổi nên BiCi = BC
Ci nằm trên đường Ax.
Nối các đoạn BiCi, ta có họa đồ chuyển vị của cơ cấu.

Trang 1
Trang 2

Trang 3

Trang 4
Trang 5

Trang 6

Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Nguyên lý máy - Chương 2: Phân tích động học cơ cấu phẳng - Nguyễn Chí Hưng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nguyên lý máy - Chương 2: Phân tích động học cơ cấu phẳng - Nguyễn Chí Hưng

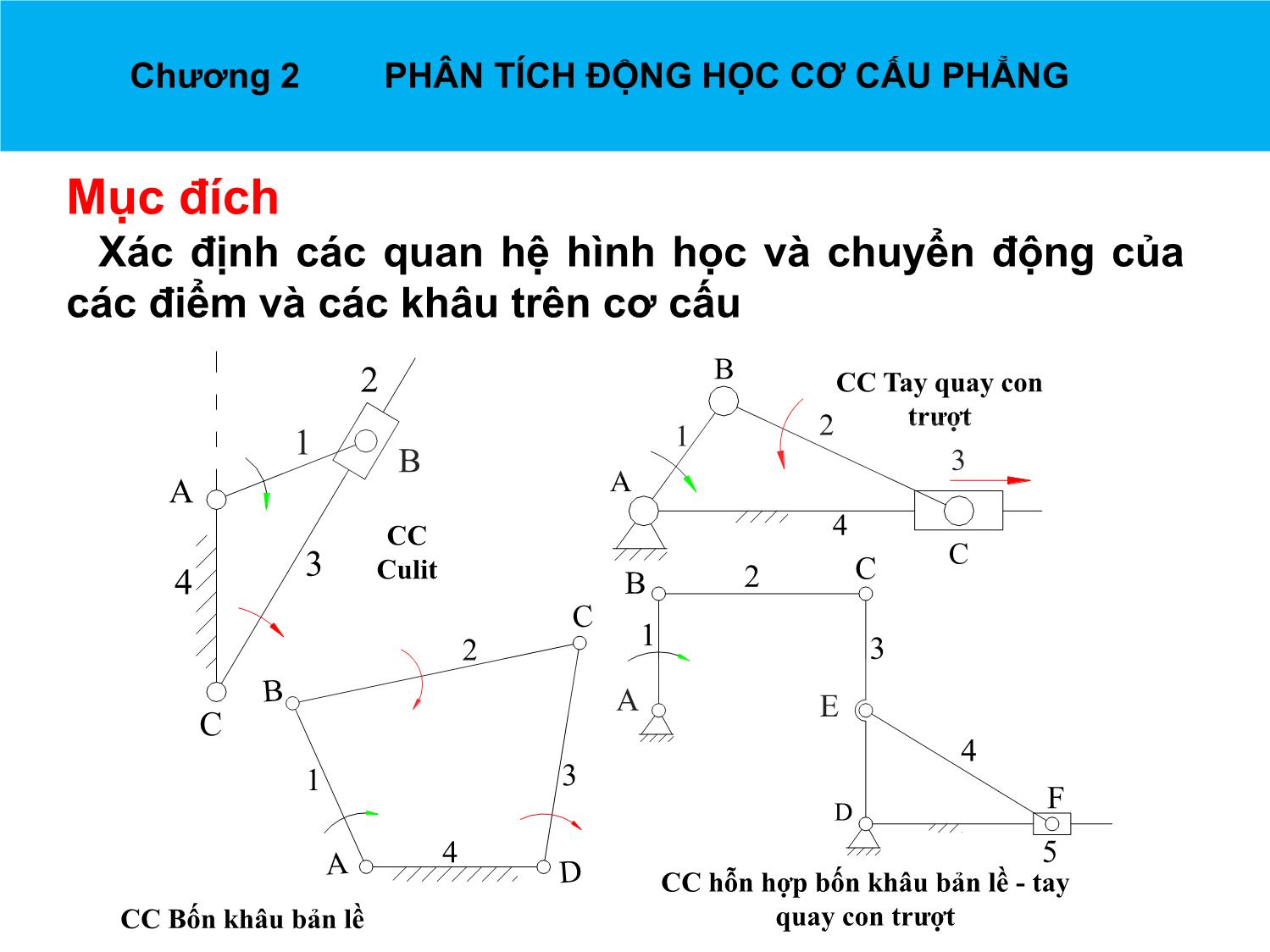
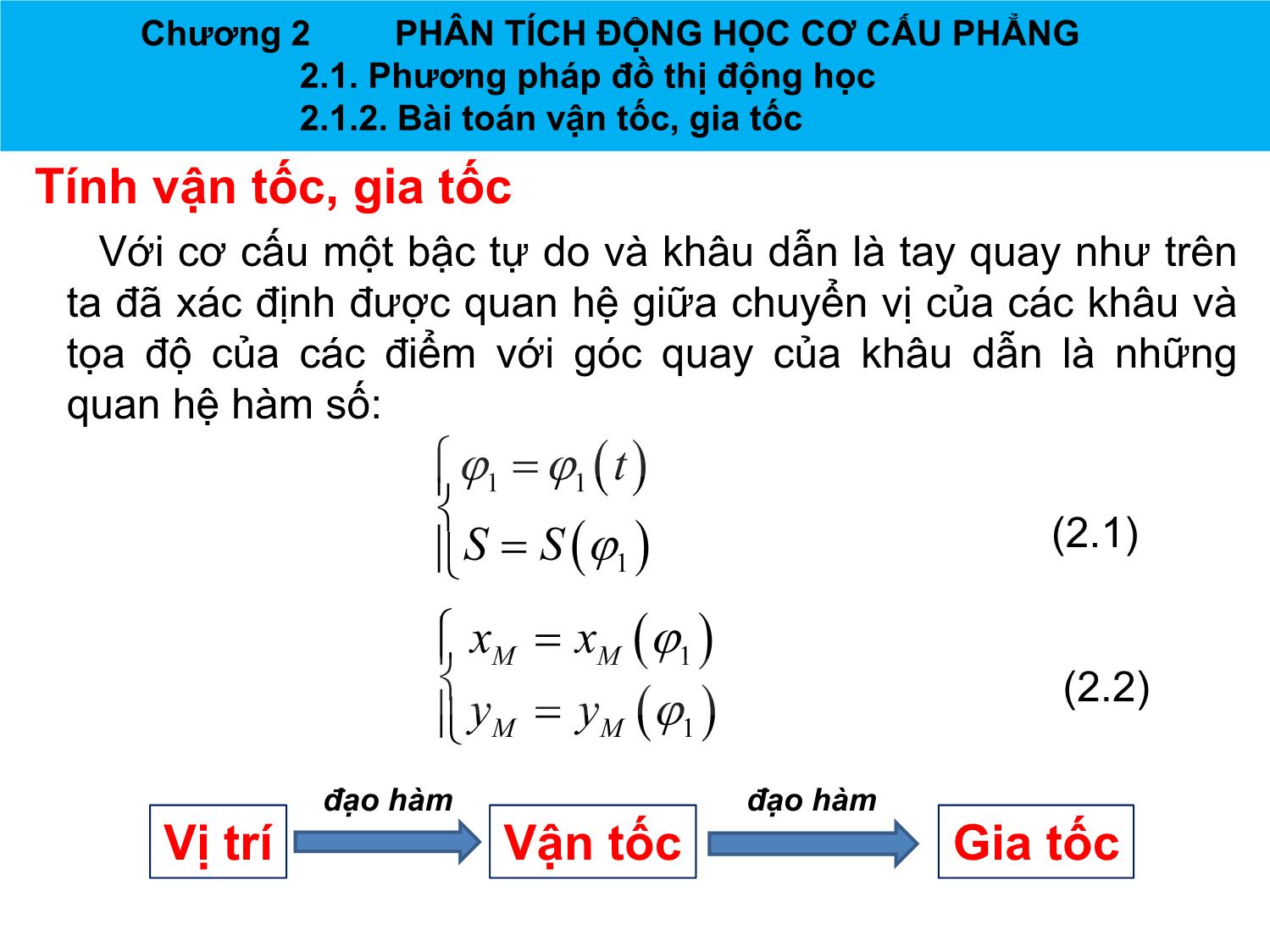
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG GV: TS. Nguyễn Chí Hưng BM: Cơ sở thiết kế máy và robot Email: hungnc-sme@mail.hut.edu.vn Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG Mục đích Xác định các quan hệ hình học và chuyển động của các điểm và các khâu trên cơ cấu 2 B CC Tay quay con trượt 1 1 2 B 3 A A CC 4 3 C 4 Culit B 2 C C 2 1 3 B A E C 4 1 3 D F A 4 5 D CC hỗn hợp bốn khâu bản lề - tay CC Bốn khâu bản lề quay con trượt Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG Phương pháp • Phương pháp đồ thị động học. • Phương pháp họa đồ véc tơ. • Phương pháp giải tích. Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo CC tay quay con trượt Đồ thị chuyển vị 1 w1 2 3 Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo Các bước thực hiện • Chọn tỷ xích của họa đồ là l • Tính độ dài các đoạn biểu diễn tương ứng với kích thước các khâu. • Vẽ quỹ đạo của tâm khớp B thuộc khâu dẫn 1, đó là đường tròn tâm A bán kính AB = lAB/l . • Chia vòng tròn (A, AB) ra n phần bằng nhau bởi các điểm Bi (i = 0 n ). Trong ví dụ này, để đơn giản ta chọn n = 8. Vẽ các vị trí ABi của tay quay. • Gọi Ci là vị trí của con trượt 3 tương ứng với vị trí ABi của tay quay. Ta có nhận xét: . Kích thước khâu 2 không đổi nên BiCi = BC . Ci nằm trên đường Ax. Nối các đoạn BiCi, ta có họa đồ chuyển vị của cơ cấu. Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo Tìm quỹ đạo của các điểm trên cơ cấu • Giả sử ta cần xác định quỹ đạo của điểm M là trung điểm của BC thuộc khâu 2. • Trên họa đồ chuyển vị, đánh dấu các vị trí Mi (i = 0 n). Nối các điểm Mi bằng một đường cong mềm quỹ đạo của điểm M. Đồ thị chuyển vị • Giả sử ta lập đồ thị S( ) biểu diễn quan hệ giữa chuyển vị S của con trượt 3 và góc quay của khâu dẫn 1. • Chọn vị trí ABo (Bo nằm trên đường thẳng Ax) làm chuẩn thì góc quay của tay quay là i = BiABo. • Đoạn CoCi chính là đoạn biểu diễn cho c.vị của con trượt tương ứng với góc quay i. Chuyển vị thực của con trượt là Si = l.CoCi. • Biểu diễn các cặp giá trị ( i,Si) trên hệ tọa độ SO , với các tỷ xích trên các trục là S và được đồ thị chuyển vị của con trượt 3. Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.2. Bài toán vận tốc, gia tốc Tính vận tốc, gia tốc Với cơ cấu một bậc tự do và khâu dẫn là tay quay như trên ta đã xác định được quan hệ giữa chuyển vị của các khâu và tọa độ của các điểm với góc quay của khâu dẫn là những quan hệ hàm số: 11 t (2.1) SS 1 xxMM 1 (2.2) yyMM 1 đạo hàm đạo hàm Vị trí Vận tốc Gia tốc Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.2. Bài toán vận tốc, gia tốc 2.1.2.1. Biểu thức tính Biểu thức vận tốc dx dx d dx v MMM ..1 w xM 1 dS dSd 1 dS dt d 11 dt d v .. w (2.3) 1 dy dy d dy dt d 11 dt d v MMM ..1 w yM 1 dt d 11 dt d Biểu thức gia tốc dSddS22 d dS dS dS a 22 w1... 1 w 1 dt dt dt dt d 1 d 1 d 1 d22 xdd dx dx dx d x a MMMMM w... w xM 22 1 1 1 dt dt dt dt d 1 d 1 d 1 (2.4) d22 ydd dy dy dy d y a MMMMM w... w yM 22 1 1 1 dt dt dt dt d 1 d 1 d 1 Trong trường hợp khâu dẫn quay đều ω1 = const, ε = 0 thu gọn ? Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.2. Bài toán vận tốc, gia tốc 2.1.2.2. Đạo hàm đồ thị Từ việc dựng hình cơ cấu xác định quỹ đạo ta dựng đồ thị quan hệ vị trí các khâu và tọa độ các điểm đối với vị trí khâu dẫn. Đạo hàm đồ thị này tìm vận tốc, gia tốc của các khâu và các điểm cần tìm. Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.1. Cách giải hệ phương trình véc tơ bằng hoạ đồ véc tơ Hệ phương trình véc tơ m m12 m mn () a ''' m m12 m mn () b ' Các véc tơ: m,, m11 m chung gốc ' Các véc tơ: m,, mnn m chung ngọn Từ đó ta thấy nếu trong phương trình (a) biết hoàn toàn các m, m ,..., m m véc tơ 1 2 (n 1) còn véc tơ n biết phương; trong phương trình (b) biết hoàn toàn các véc tơ m''', m ,..., m 1 2 (n 1) còn véc tơ m' biết phương. n Ta có thể dùng hoạ đồ véc tơ để giải tìm véc tơ m Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ vận tốc Hai điểm A, B trên cùng khâu VA Trong đó B vv, V ABlà vận tốc tuyệt đối các B điểm B, A VBA w vBA là vận tốc tương đối của B khi quay quanh điểm A, vBA BA, chiều theo chiều quay A VA của w,vlBA w. AB vB v A v BA Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ vận tốc Hai điểm Bi và Bk trùng nhau tức thời trên hai khâu i và k (i, k nối với nhau bằng khớp tịnh tiến) i r Trong đó V Bi Bk vv, BBiklà vận tốc tuyệt đối các điểm trên hai khâu r k v là vận tốc trong chuyển động B i Bk tương đối của Bi với Bk, Bi Bk // phương tịnh tiến giữa khâu i và khâu k. k= i wk= wi r vBB v v i k BiBk Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định vận tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định vận tốc Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ gia tốc của các điểm Khi hai điểm A, B trên cùng khâu Trong đó aA aa, B t ABlà gia tốc tuyệt đối các aBA điểm A,B. n aBA aBA là gia tốc trong chuyển aBA a B động tương đối của B quanh A n w aBA hướng từ B → A, là A a A thành phần gia tốc pháp tuyến (hướng tâm); nt a a a a a a n 2 B A BA A BA BA alBA w AB Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ gia tốc của các điểm Hai điểm Bi và Bk trùng nhau tức thời trên hai khâu i và k i Trong đó r r a VB B aa, Bi Bk i k BBkilà gia tốc tuyệt đối các điểm A,B. avk 2.w BBBBi k i k k là gia tốc Cô-ri-ô-lít trong chuyển k động tương đối của Bk và Bi. Do B B a r k i k BiBk w v nên av 2.w . và BBik BBBBi k i k chiều là chiều của v r quay đi 900 BBik k= i theo chiều quay của ω. = wk wi r aBB là gia tốc trong chuyển động kr ik a a a a tương đối của Bi với Bk BBBBBBi k i k i k Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc Kết luận Phân tích động học bằng phương pháp tâm vận tốc tức thời C V B B 13 2 3 V 1 A13 4 P 13 A D Hình 2-12 Phân tích động học bằng phương pháp tâm vận tốc tức thời Ví dụ phân tích động học bằng phương pháp tâm vận tốc tức thời Ví dụ phân tích động học bằng phương pháp tâm vận tốc tức thời Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.1. Bài toán vị trí Phương trình lược đồ động Phương trình vectơ của lược đồ động Cơ cấu bốn khâu phẳng toàn khớp thấp có dạng một tứ giác. Nếu biểu diễn các cạnh của đa giác lược đồ động này bằng các vectơ nối tiếp nhau ta sẽ được một chuỗi vectơ khép kín. Gọi là vectơ thứ i của chuỗi, y ta có phương trình vectơ sau: 4 4 l 3 l 0 le 0 (2.5) 2 i ii e2 i 1 i 1 l 2 e - vector đơn vị chỉ phương 1 e i e 3 1 li - chiều dài vector li 1 Phương trình hình chiếu l 4 4 ex l 3 l cos 0 no i i i 1 x 4 (2.6) e4 4 eo l sin 0 i i O eo x i 1 Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.1. Bài toán vị trí y Tọa độ các đỉnh của đa giác lược đồ động y j 2,(2.16) Các đỉnh của đa giác lược đồ động được ký 2 y1, j hiệu bằng các số 0, 1, 2, 3 theo quy ước sau: l Đỉnh số i là gốc của véctơ . Như vậy đỉnh số y 0 0 bao giờ cũng ứng với khớp bản lề nối 0, j khâu dẫn với giá. no y 3 Gọi x0, y0 là tọa độ của đỉnh số không trong 3, j hệ tọa độ gắn liền với giá. Tọa độ của đỉnh O x j e x j x j x j số k của đa giác lược đồ động khi đó sẽ 0, o 1, 2, 3, x Hình 2-19 bằng: k xki x0i l cos i 1 (k 0,1, 2, 3) k yki y0i l sin i 1 Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.2. Bài toán vận tốc Phương trình vận tốc Phương trình vectơ vận tốc 33 d dlii de Đạo hàm (2.5): li e i e i l i 0 dtii 11 dt dt 3 dl de d i ii (w l n l e ) 0 (2.6) Với li và nniw i i ta có: i i i i i dt dt dt i 1 Phương trình hình chiếu vận tốc 3 3 (w l n l e ) e 0 x e0 i i i i i 0 (lli cos i w i i sin i ) 0 i 1 i 1 (2.6) (2.7) 3 3 (w l n l e ) n 0 (lli sin i w i i cos i ) 0 x n0 i i i i i 0 i 1 i 1 Từ (2.7) lii,w (giải bài toán vận tốc) Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.3. Bài toán gia tốc Phương trình gia tốc Nội dung của bài tính gia tốc là cho trước kích thước động các khâu, vị trí khâu dẫn, vận tốc góc và gia tốc góc của khâu dẫn, cần phải xác định gia tốc của tất cả các khâu của cơ cấu. Gia tốc của một khâu coi như xác định khi ta biết: - Hoặc gia tốc góc của nó và gia tốc dài của một điểm bất kỳ trên nó. - Hoặc gia tốc dài của hai điểm trên khâu Để giải bài tính gia tốc trước hết phải giải xong bài tính vị trí và vận tốc, do đó khi giải bài tính gia tốc tất cả các đại lượng lli,,, w i i i đều đã biết. Phương trình vectơ gia tốc d 3 Lấy đạo hàm theo t các hạng (2.8) (wil i n i l i e i ) 0 thức vế trái của (2.6) ta được: dt i 1 Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.3. Bài toán gia tốc Phương trình gia tốc Đặt d dl w , i l idt i dt i dn i w e dt ii 3 2 (2.9) (2.8) ( wiiil e iii l n 2 w iii l n l ii e ) 0 i 1 Với w2le là véctơ gia tốc pháp tuyến hướng tâm i i i iln i i là véctơ gia tốc tiếp tuyến 2wiln i i là véctơ gia tốc gia tốc Côriôlít leii là véctơ gia tốc tương đối giữa hai điểm khác khâu và hiện thời trùng nhau Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.3. Bài toán gia tốc Phương trình gia tốc Sau khi giải bài tính vị trí và bài tính vận tốc thì các đại lượng sau đây trong phương trình (2.7) đã biết: - Các véctơ enii, - Các đại lượng wii, l Trong sáu đại lượng còn lại có mặt trong phương trình (2.9) chỉ có ba đại lượng khác không, trong đó đã ii,li ( 1, 2, 3) 1 cho. Do đó phương trình (2.9) chỉ có hai ẩn và như vậy có nghiệm xác định. Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.3. Phương pháp véc tơ – giải tích 2.3.3. Bài toán gia tốc Phương trình hình chiếu của gia tốc 3 2 x e0 ( wiil cos iii l sin i 2 w ii l sin ii l cos i ) 0( a ) i 1 (2.9) 3 2 x n0 ( wiil sin iii l cos i 2 w ii l cos ii l sin i ) 0( b ) i 1 (2.10) Sau khi giải hệ phương trình (2.10) ta xác định được giá trị của hai đại lượng và giá trị của đã cho trong giả thiết lii, ta có thể suy ra trong mỗi khâu gia tốc dài của hai điểm hoặc gia tốc góc của nó và gia tốc dài của một điểm thuộc nó, tức là bài tính gia tốc đã giải xong. Bài tập chương 2 Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập lAB=lAC 3 C Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Bài 3: Tính vận tốc và gia tốc điểm F trong cơ cấu máy sàng lắc nếu tay quay quay đều với vận tốc góc w1 = 20rad/s tại vị trí AB và CD thẳng đứng, BC nằm ngang. Cho biết kích thước các khâu: Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập Ví dụ và bài tập
File đính kèm:
 bai_giang_nguyen_ly_may_chuong_2_phan_tich_dong_hoc_co_cau_p.pdf
bai_giang_nguyen_ly_may_chuong_2_phan_tich_dong_hoc_co_cau_p.pdf

