Bài giảng Kỹ thuật truyền thông - Chương 4: Mã hóa nguồn
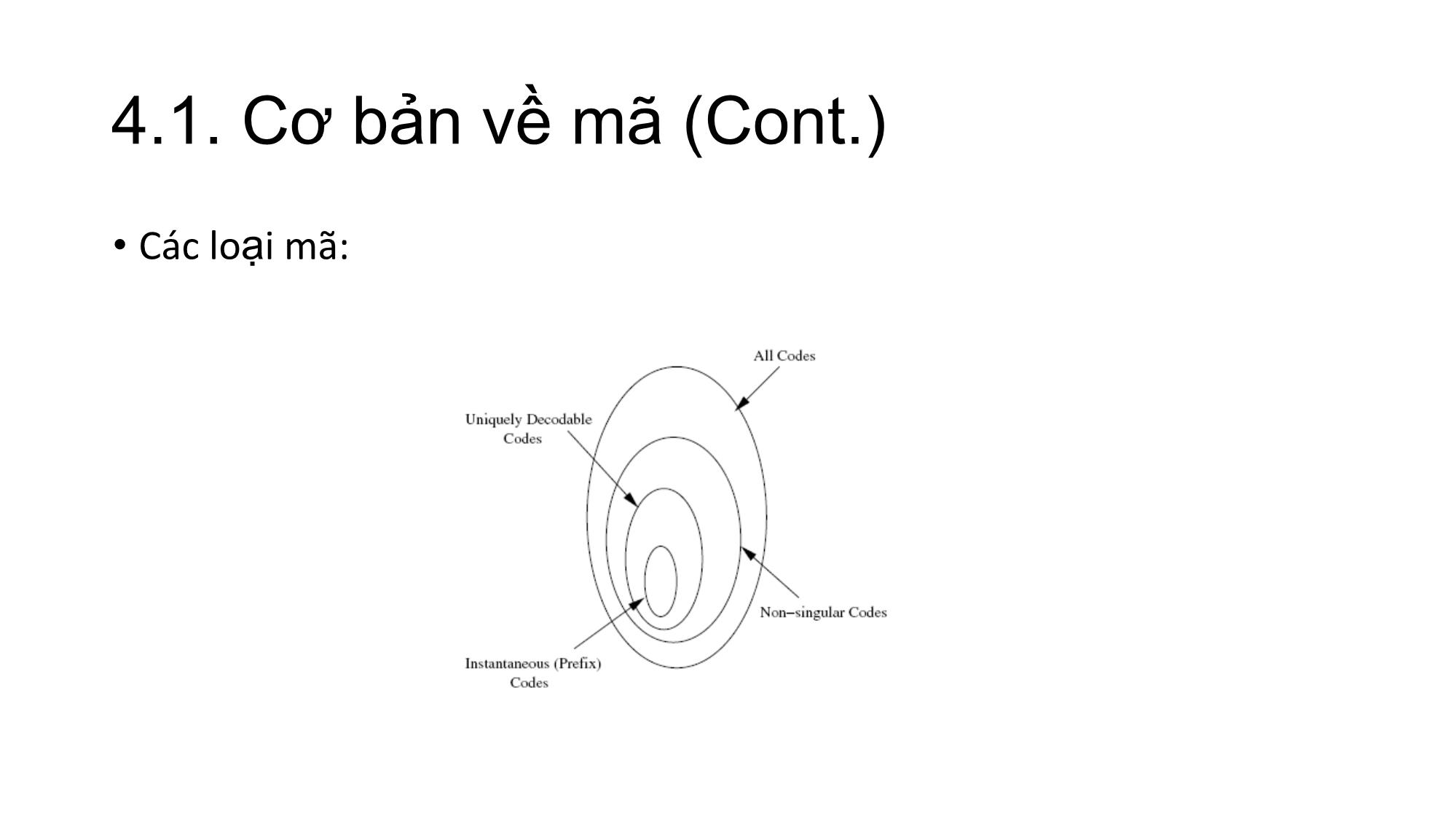
Cơ bản về mã hóa
• Tại một thời điểm, nguồn tạo ra một ký hiệu từ bảng ký hiệu của
nguồn
• Thông thường, bảng chữ là hữu hạn
• S = {s1, s2, , sq} Ở đây q là ||S|| hoặc sô ký hiệu của nguồn S
• Mã hóa: Sử dụng một tập hữu hạn các ký hiệu mã để biểu diễn các
ký hiệu của nguồn
• Có thể biểu diễn tập ký hiệu mã bởi tập X = {x1, x2, ,xr}. Ví dụ với mã BCD, X
= (0,1), r=2
• r là ||X|| hay số ký hiệu mã khác nhau
• được gọi là cơ số của mã
• r = 2 : mã nhị phân
• r ≠ 2: mã r trị

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kỹ thuật truyền thông - Chương 4: Mã hóa nguồn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật truyền thông - Chương 4: Mã hóa nguồn

• Example:
• Original Source :
4.6.2. Mã số học - Thuật toán mã hóa
Bản tin rỗng sẽ được coi tương ứng với một điểm bất kỳ trong đoạn
[0,1). Điểm đầu I(0) = 0, điểm cuối U(0) = 0.
Với bản tin dài n, thuật toán mã hóa bản tin sẽ lần lượt tìm điểm đầu,
điểm cuối cho bản tin dài n = 1, 2,.. là I(n), U(n). Công thức tính lần
lượt các điểm này như sau:
I(n) = I(n-1) + {U(n-1) – I(n-1)} F(sn-1)
U(n) = I(n-1) + {U(n-1) – I(n-1)} F(sn)
Với ánh xạ S ={si: i=1,..,q} = {1,..,q}. Tin sn là tin nằm ở cuối bản tin. F(sn-1) là hàm
phân bố xác suất của tin ở trước tin sn trong tập tin của nguồn.
Chứng minh được I(n) >= I(n-1) và U(n) <= U(n-1). Đoạn của bản tin dài hơn nằm
trong đoạn của bản tin ngắn hơn
4.6.2. Mã số học - Thuật toán mã hóa
Sau khi xác định điểm đầu điểm cuối của đoạn chứa bản tin, điểm biểu
diễn bản tin được chọn là điểm có giá trị là phân số nhị phân bé nhất trong
đoạn đó. Phần phân số nhị phân của điểm này sẽ được lấy làm mã mã
hóa bản tin.
Điểm biểu diễn bản tin nằm trong các đoạn biểu diễn các bản tin rút
gọn còn 1, 2, 3, .., n tính từ đầu bản tin.
Với mã số học r trị thì chọn điểm biểu diễn từ mã là điểm có giá trị bằng
phân số r phân ngắn nhất trong đoạn và phần phân số này là mã của bản
tin.
Mã số học cho độ dài trung bình của từ mã Hr(S) <= L <= Hr(S) + 2/n. N
độ dài bản tin.
4.6.2.Mã số học - thuật toán mã hóa
Ví dụ: Nguồn S = {a,b,c} có P(S) = {0.7, 0.1, 0.2} và bản
tin m = acb
Hàm phân bố xác suất F(si):
si = a -> x = 1
si = b -> x = 2
si = c -> x = 3
4.6.2.Mã số học - thuật toán mã hóa
Khi chưa mã hóa (bản tin rỗng) bản tin sẽ là điểm bất kỳ trong đoạn [0,1) hay I(0) =0 và U(0) =1
Với ký hiệu đầu, bản tin là a:
I(1) = I(0) + [U(0) - I(0)]F(si = rỗng) = 0 + (1 -0)0 = 0
U(1)= I(0) + [u(0) – I(0)]F(si=a) = 0 + (1 – 0) 0.7 = 0.7
Với ký hiệu thứ hai, bản tin là ac:
I(2) = I(1) + [U(1) – I(1)] F(b) = 0 + (0.7 – 0) 0.8 = 0.56
U(2) = I(1) + [U(1) – I(1)]F(c) = 0 + (0.7 -0) 1= 0.7
Với ký hiệu thứ ba, bản tin là acb:
I(3) = I(2) + [U(2) – I(2)] F(a) = 0.56 + (0.7 – 0.56)0.7 = 0.658
U(3) = I(2) + {U(2) – I(2)} F(b) = 0.56 + (0.7 -0.56) 0.8 = 0.672
Chọn điểm biểu diễn bản tin là 0,6640625 có giá trị nhị phân 0.1010101 có số chữ số nhị phân ngắn
nhất trong đoạn [0.658, 0.672]. Mã của bản tin sẽ là 1010101.
4.6.2. Mã số học - Thuật toán giải mã
Mã của bản tin là chuỗi nhị phân nằm trong đoạn biểu diễn
bản tin con dài 1,2,.., n tin của bản tin (tính từ đầu bản tin)
Bắt đầu từ đầu chuối mã nhận được chúng ta sẽ xác định
đoạn chứa điểm có giá trị bằng phân số ứng với chuỗi mã nhị
phân dài 1, 2,.. chữ số nhị phân. Khi đoạn chứa chuỗi mã nhị
phân nằm trong đoạn chứa bản tin con dài n = 1,2,.. ta tách ra
được bản tin dàicon n của bản tin.
Liên tiếp tìm các tin cho đến khi hết tin của bản tin.
Mã số học không cần truyền bảng mã đến nơi nhận.
4.6.2. Mã số học - Thuật toán giải mã
Ví dụ: Với nguồn S = (a,b,c) với P(S) = (0.7, 0.1, 0.2) và bản tin m = acb
được mã hóa 1010101.
Với cách mã hóa số học bản tin a nằm trong đoạn [ 0, 0.7], ac nằm trong
đoạn [0.56, 0.7] , acb nằm trong đoạn [0.658, 0.672].
Chuỗi mã nhận được là 101010
Ký hiệu mã đầu 1 ứng với giá trị 0.1 nhị phân, nằm trong đoạn [0.100..,
0.111..] nhị phân hay [0.5,1] chưa cho phép xác định tin đầu tiên vì đây là
khoảng chứa ký hiệu đầu có thể là a hoặc b hoặc c.
Thêm ký hiệu 10 ứng với giá trị 0.10 nhị phân, nằm trong đoạn [0.1000..,
0.10111..] nhị phân hay [0.5, 0.75], ký hiệu đầu có thể là a hoặc b
4.6.2. Mã số học - Thuật toán giải mã
Thêm ký hiệu tiếp 101 ứng với giá trị 0.101 nhị phân, nằm trong khoảng [0.10100..,
0.10111..] hay [0.625, 0.75], ký hiệu đầu vẫn có thể a hoặc b
Thêm ký hiệu tiếp 1010 ứng với giá trị 0.1010, nằm trong khoảng [0.101000..,
0.101011..] hay [0.625, 0.6875]. Đoạn này nằm trong đoạn của tin đầu là a, [0, 0.7]
và trong đoạn của tin thứ hai là c, [0.56, 0.7]. Vậy tin đầu của bản tin là a và tin thứ
hai là c.
Tiếp tục 10101 ứng với đoạn [0.65625, 0.6875], 101010 ứng với đoạn [0.65625,
0.67185] không nằm trong đoạn [0.658, 0.672] nên không giải mã được.
Mã 1010101 ứng với đoan [0.6640625, 0.671875] nằm trong đoạn [0.658, 0.672]
ứng với bản tin acb. Vậy bản tin là acb.
So với mã Huffman, bản tin acb có 6 ký tự. Tuy nhiên nếu phải mở rộng nguồn thì
mã số học có hiệu suất mã khá tốt so với Huffman
4.7. Mã hóa nguồn với mã có độ dài cố
định
•
4.7. Mã hóa nguồn với từ mã có độ dài
cố định (Cont.)
•
4.8. Mã hóa theo loạt dài (Run-length
coding)
• Mã hóa theo loạt dài (RLC) là cách đơn giản và hiệu quả để nén dữ
liệu khi một tin xuất hiện liên tiếp nhau trong bản tin.
• Mã này là thích hợp cho một số loại dữ liệu ảnh, nhưng không luôn tích hợp
cho văn bản vì rất hiếm khi một ký tự văn bản xuất hiện 2 lần liên tiếp nhau.
• Để nén một chuỗi tin giống nhau, mã hóa theo loạt dài đơn giản thay
chuỗi này bằng 1 tin của chuỗi và tiếp theo là số lần lặp tin này của
chuỗi
• Bên giải mã, cần phân biệt mã của số lần lặp và tiến hành phục hồi
lại chuỗi tin
4.9. Mã Lempel Ziv
• Mã hóa theo từ điển:
• Tạo một danh sách các từ và số thứ tự xuất hiện của từ này trong dạng văn
bản của bản tin. Danh sách này được gọi là từ điển
• Chuyển văn bản của bản tin thành chuỗi các chỉ thị chỉ ra điểm vào của từ
trong từ điển. Bản tin chuyển thành chuỗi các chỉ số.
• Khi giải mã từ chuỗi chỉ số là các điểm vào của từ trong từ điển phục hồi lại
các từ của bản tin.
• Mã này phù hợp cho bản tin chuyển về được dạng văn bản.
• Mã Lempel-Ziv là mã theo từ điển và có nhiều biến dạng. Chúng ta chỉ quan
tâm đến hai biến dạng LZ77 và LZ78.
4.9.1. LZ77
• Xây dựng từ theo luật:
• Mỗi “từ mới” là một “từ cũ” thêm một ký tự tiếp theo trong văn bản
• Mỗi từ được biểu diễn bởi một bộ ba (m,n,c)
• n (n >1) là số ký hiệu của chuỗi tìm được trùng với một chuỗi đã xuất hiện trước
nó (“từ cũ”.
• c là ký hiệu tiếp theo chuỗi tìm được.
• m là số vị trí cần phải quay ngược lại để tìm thấy điểm đầu của chuỗi đã tìm được.
• Bộ ba đầu tiên là (0,0,c). C là ký tự nguồn đầu tiên. Từ đầu tiên là từ rỗng nằn ở vị
trí 0 trong văn bản.
. Văn bản được chuyển thành chuỗi các bộ ba ứng với các từ tìm được.
. Quá trình giải mã:
• Bắt đầu từ bộ ba đầu tiên, dần dần phục hồi lại các từ theo chuỗi các bộ ba nhận
được.
4.9.1. LZ77
• Văn b: the_fat_cat_sat_on_the_mat.
• Chuỗi các bộ ba:
• Bắt đầu từ đầu bản tin : (0,0,t), (0,0,h), (0,0,e),(0,0,_), (0,0,f), (0,0,a), (0,0,t),
(0,0,_),(0,0,c), (4,3,s),(4,3,o), (0,0,n), (0,0,_), (19,4,m), (11,2,.)
• Giải mã:
• (0,0,t)->t, (0,0,h)->h (th), .. (0,0,c)->c(the_fat_c),
(4,3,s) (the_fat_cat_s).
4.9.1. LZ78
• Từ rỗng coi là từ nằm ở vị trí 0 trong từ điển.
• Từ có ví trí 1 tìm được là từ có 1 ký hiệu là ký hiệu đầu của văn bản. Từ
này là từ cũ (rỗng lấy thêm một ký tự đầu của văn bản). Từ nảy được tách
ra khỏi văn bản.
• Tiếp tục tìm các từ có thứ tự tìm được tiếp theo dựa vào nguyên tắc “từ
mới” là chuối ký hiệu của “từ cũ” và lấy thêm 1 ký hiệu tiếp theo trong
văn bản. Từ này được tách khỏi văn bản. Tiếp tục như vậy cho đến khi
hết văn bản.
• Mỗi từ được biểu diễn bởi một cặp (i,c)
• i là số thứ tự tìm thấy từ
• c là ký tự lấy thêm
• Văn bản là chuỗi các cặp (i,c)
4.9.2. LZ78
• Text: the_fat_cat_sat_on_the_mat.
4.10. Mã nguồn liên tục
•
4.10. Mã nguồn liên tục
Mã hóa nguồn cho nguồn liên tục là mã hóa bản tin được
nguồn tạo ra với số ký hiệu mã phải sử dụng là tối thiểu
Mã nguồn tối ưu có độ dài trung bình từ mã L = Hr(S) cho số
ký hiệu mã phải sử dụng để mã hóa bản tin là tối thiểu
Nguồn liên tục được coi là có số tin tạo ra trông 1 đơn vị thời
gian bằng số mẫu của nguồn rời rạc tương đương (Ts =
1/(2Fmax))
Lượng tin trung bình của mỗi mẫu sẽ là Hr(S) nên số ký hiệu
mã để mã hóa mỗi mẫu sẽ là L >= Hr(S). Lmin = Hr(s)
4.10. Mã nguồn liên tục
Mã hóa nguồn cho nguồn liên tục có thể có các phương pháp:
Mã hóa theo thời gian là mã hóa bản tin được biểu diễn
theo thời gian
Mã hóa theo tần số là mã hóa bản tin được biểu diễn theo
tần số
Mã hóa mô hình nguồn là tìm mô hình toán học cho nguồn
và mã hóa các tham số của mô hình
4.10.1. Mã nguồn liên tục theo thời gian
Mã hóa bản tin là chuyển bản tin thành chuỗi các từ mã hay thành
chuỗi ký hiệu mã Mã hóa nguồn cần thực hiện hai nhiệm vụ:
Chuyển đổi bản tin tạo ra từ tương tự sang số (ADC)
Giảm số ký hiệu mã đến tối thiểu (hay nén dữ liệu).
ADC bao gồm 3 thao tác kế tiếp
Lấy mẫu
Lượng tử hóa
mã hóa (thường là mã nhị phân)
4.10. Mã nguồn liên tục theo thời gian
• Hai nhiệm vụ của mã hóa nguồn cho nguồn liên tục có thể thực hiện song
song hoặc theo thứ tự:
• Nén trước khi ADC (nén tương tự):
• Nén biên độ.
Luật nén A: giả sử biên độ x có 0<= |x| <=1. X’ = sign(x){A|x|/(1+lnA)}, khi |x| <=1/A và
x’ = sign(x){(1 + ln(A|x|)/(1+lnA)}, khi 1/A < |x| <=1.
• Nén tần số
Tần số Mel: m = 2595lg(1 + f/700). Với f là tần số đo bằng Hz.
• Song song (nén và các thao tác của ADC xen nhau): Ví dụ PCM kết hợp nén và mã
hóa Delta.
• Lấy mẫu
• Tính giá trị Delta (đạo hàm rời rạc) để nén chênh lệch biên độ trung bình giữa hai mẫu liên
tiếp.
• Lượng tử hóa Delta (cùng sai số nhưng delta sẽ giảm số giá trị lượng tử)
• ADC trước khi nén:
• Đây là thuật toán nén nguồn rời rạc.
4.10. Mã nguồn liên tục theo thời gian
• Với nguồn ảnh thì mỗi ảnh được chia thành các điểm ảnh (Pixel) theo lưới chia
tạo thành bởi các đường song song với hai cạnh của ảnh và cách nhau dưới góc
nhìn nhỏ hơn hoặc bằng góc phân biêt.
• Thông tin của ảnh là thông tin từ từng điểm của ảnh. Việc đọc thông tin từ các
điểm ảnh là thực hiện đọc từng dòng từ trái qua phải và lần lượt từ dòng trên
xuống dưới.
• Với ảnh động thì sau khi đọc hết thông tin của 1 ảnh sẽ quay lại đọc từ phần tử
góc trên bên trái của ảnh mới
• Thông tin của ảnh là rời rạc theo thời gian nhưng liên tục theo mức. Trong
trường hợp số hóa thì thông tin của mỗi điểm ảnh sẽ được lượng tử hóa
thường là 256 mức (1 byte)
• Thông tin của 1 điểm ảnh thường bao gồm 1 thông tin về độ chói (Britgh) với
lưới chia theo góc phân biệt 2 phut và 3 thông tin màu với lưới chia theo góc
phân biệt 5 phút.
4.10. Mã nguồn liên tục theo thời gian
• Việc nén thông tin của 1 ảnh còn gọi là nén ảnh tĩnh thường là tìm
cách mã hóa để tạo ra chuỗi điểm ảnh có thông tin giống nhau liên
tiếp và áp dụng mã RLC
• Việc nén ảnh động thường là truyền thông tin 1 ânh đầu và sau đó
tìm các thông tin thay đổi của ảnh sau so với ảnh trước và chỉ truyền
các thông tin sai khác của ảnh sau.
4• ..10.1 PCM
4.10.1. PCM
Để giảm số bit dùng mã hóa PCM áp dụng thêm một luật
nén:
Nén biên độ trước PCM làm cho dải động Xmax – Xmin
giảm dẫn đến số mức lượng tử M = (Xmax – Xmin)/
Vref +1 giảm số bit mã hóa mỗi mẫu n = log2(M)
giảm
Tính giá trị Delta = mẫu(i) – mẫu(i-1). Delta là đạo hàm
rời rạc của bản tin nên dải động của Delta sẽ bé hơn
4• .10. .1. Mã hóa delta
4.10.2. Mã hóa theo tần số
Mã hóa nguồn liên tục theo tần số sẽ mã hóa phổ bản tin được tạo
ra.
Thông thường các giải pháp mã hóa tần số là mã hóa tham số
ước lượng tham số của phổ rồi mã hóa nó
Do nguồn nói chung có mô hình là quá trình ngẫu nhiên ergodic nên
tham số biến thiên chậm lấy mẫu thưa hơn và dải động nhỏ
Hai kỹ thuật hay được sử dụng là mã hóa theo dải băng tần con và
mã hóa theo các thành phần cơ bản (ví dụ mã hóa formant)
4.10.2. Mã hóa theo dải băng tần con
Mã hóa theo băng tần con dựa vào khái niệm băng tần tới hạn (Critical
Band) của các cơ quan cảm nhận: cơ quan cảm nhận không phân biêt
được độ cao của từng tần sô riêng mà theo từng dải tần số == Băng tới
hạn
Ví dụ tai người phân biệt các băng tần số (giống như sử dụng bộ lọc thông
dải) có tần số trung tâm và độ rộng của băng tăng dần theo tần số
.
4.10.2. Mã hóa theo dải băng tần con
Dải tần số tai người nghe tốt sẽ có 24 băng tới hạn,
mỗi băng gọi là 1 Bark (hay tính theo độ đo Bark)
Mã hóa theo dải băng tần con sẽ sử dụng một hệ
thống các mạch lọc thông dải có tham số tương ứng
với tham số của các băng tới hạn. Các đầu ra của các
mạch lọc là biên độ trung bình của tín hiệu của mỗi
Băng con.
Bên giải mã sẽ sử dụng hệ thống mạch lọc giống bên
mã hóa với đầu vào là nhiễu trắng. Hệ số truyền đạt
của các mạch lọc này là đầu ra của các bộ lọc mã
hóa. MP3 là loại mã này cho âm thanh.
4.10.2. Mã hóa theo formant
Hình bên là khái niệm formant trong phổ
Hình dưới là phổ đồ (spectograme) của đoạn âm thanh
4.10.2. Mã hóa theo mô hình nguồn
Phương pháp mã hóa theo mô hình nguồn là phương pháp tìm mô hình toán học
cho nguồn từ bản tin được tạo ra
Phương pháp mã hóa theo mô hình nguồn được ứng dụng nhiều trong thực tế xử lý
âm thanh là mã hóa dự đoán tuyến tính (Linear Predictive Coding).
Phương pháp mã hóa dự đoán tuyến tính coi mỗi mẫu tín được tạo ra s[n] là tổ hợp
tuyến tính của các mẫu tạo ra trước nó s[n – k]
Ở đây ak là các hệ số cần tìm của bộ dự đoán cấp p, e[n] là sai số dự đoán mẫu
s[n], p Nếu dự đoán đúng thì sai số e[n] =0. Hay phương trình trên khi e[n] = 0 là
phương trình sai phân của 1 nguồn tạo ra các mẫu tin s[n]
4.10.2. Mã hóa theo mô hình nguồn
Phương trình trên có thể coi là phương trình sai phân của 1 hệ tuyến tính bất
biến với đầu vào là e[n] và đầu ra s[n]. Hàm truyền của hệ trong không gian z:
Đây là mô hình của hệ chỉ có các điểm cực hay hệ tự hồi quy
(AutoRegressive)
Để hệ trên trở thành mô hình nguồn ta cần tìm các hệ số ak sao cho e[n] -> 0
(đạt giá trị cực tiểu)
4.10.2. Mã hóa theo mô hình nguồn
Chọn các ak để cực tiểu hóa e[n] có thể đạt được bằng cách cực tiểu hóa năng
lượng sai số khi chọn các ak theo phương trình
Đạo hàm phương trình trên theo từng hệ số ak và tìm giá trị ak cho phương trình
đạo hàm bằng 0 sẽ là hệ p phương trình với các hệ số ak cho năng lượng tối thiểu
cho phép giải ra các hệ số ak và sai số dự đoán e[n]
Kết quả là tập hệ số ak của mô hình nguồn và sai số dự đoán e[n] tối thiểu tìm được
là đầu vào của mô hình. Đây là các tham số trong mã hóa mô hình nguồn.
Bên giải mã sẽ là hệ tự hồi quy với tập hệ số ak và đầu vào là e[n].
Bài tập
Bài 4: Giả sử nguồn tin chỉ tao một bản tin có nội dung là ‘công nghệ
thông tin’ viết ở dạng tiếng Việt không dấu, không phân biệt chữ
thường chữ hoa và không có dấu cách giữa các từ. Mỗi ký tự trong
bản tin là 1 tin được tạo ra từ nguồn. Xác suất xuất hiện của mỗi tin
là tần suất xuất hiện của nó trong bản tin.
a. Hãy mã hóa bản tin trên theo mã Huffman với cơ số mã r = 4.
b. Tính hiệu suất của mã
c. Cần mở rông nguồn bao nhiêu lần ở hiệu suất mã đạt ít nhất 98%
Bài 5: Hãy mã hóa bản tin ở câu 4 bằng mã LZ77 và bằng mã LZ78File đính kèm:
 bai_giang_ky_thuat_truyen_thong_chuong_4_ma_hoa_nguon.pdf
bai_giang_ky_thuat_truyen_thong_chuong_4_ma_hoa_nguon.pdf

