Bài giảng Giải tích II - Chương 1: Mở đầu, giới hạn, liên tục - Nguyễn Văn Quang

 GIẢI TÍCH II 
 Trường Đại học Công nghệ 
 Đại học Quốc gia Hà nội 
Giảng viên: TS. Nguyễn Văn Quang 
E-mail: nvquang.imech@gmail.com 
 Đánh giá kiểm tra: 
  A: Điểm thành phần (40%) 
 o Điểm chuyên cần, điểm bài tập: 10% 
 o Điểm thi giữa kỳ: 30% 
  B: Điểm thi cuối kỳ (60%) 
  Điểm kết thúc môn học = A*0.4 + B*0.6 
 TS. Nguyễn Văn Quang 
02-Feb-21 2 
 Đại học Công nghệ - ĐHQGHN 
 Tài liệu: 
 1. Nguyễn Đình Trí. Toán học cao cấp, tập 3. 
 NXB Giáo dục, 2006. 
 2. Nguyễn Thủy Thanh. Bài tập giải tích, tập 
 1,2,3. NXB Giáo dục, 2002. 
 3. Trần Đức Long. Bài tập Giải tích, tập 1,2,3. 
 NXB ĐHQGHN, 2005. 
 4. Nguyễn Thừa Hợp. Giải tích, tập 1,2,3. NXB 
 ĐHQGHN, 2004. 
 5. James Stewart. Calculus, 7th Edition, 2010. 
 TS. Nguyễn Văn Quang 
02-Feb-21 3 
 Đại học Công nghệ - ĐHQGHN 
 Nội dung: 
 • Chương 1: Mở đầu, giới hạn, liên tục 
 • Chương 2: Đạo hàm, vi phân 
 • Chương 3: Tích phân bội hai 
 • Chương 4: Tích phân bội ba 
 • Chương 5: Tích phân đường 
 • Chương 6: Tích phân mặt 
 • Chương 7: Phương trình vi phân 
 TS. Nguyễn Văn Quang 
02-Feb-21 4 
 Đại học Công nghệ - ĐHQGHN 
 1. Hàm hai biến 
 2. Mặt bậc hai 
 3. Giới hạn 
 4. Liên tục 
 TS. Nguyễn Văn Quang 
02-Feb-21 5 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa 
 Cho DR  2 . Hàm hai biến là một ánh xạ: 
 f: D R
 (,)(,)x y f x y
 Ký hiệu: f f( x , y ).
 được gọi là miền xác định của . 
 Miền giá trị của : E { a R |  ( x , y ) D : a f ( x , y )}
 Nếu cho bởi biểu thức đại số: Miền xác định là tập hợp tất cả 
 các giá trị của và , sao cho biểu thức có nghĩa. 
 Miền giá trị là tập hợp tất cả các số thực mà hàm có thể nhận được. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 6 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Hàm hai biến: 
 + + 1
 , = 
 − 
 Miền xác định: D {}( x , y ) R2 | x y 1 0, x y
 3 2 1
 f (3,2) 6
 32 
 TS. Nguyễn Văn Quang 
 02-Feb-21 7 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Phương trình tổng quát mặt bậc hai trong hệ tọa độ Descartes là: 
 Ax2 By 2 Cz 2 22 Dxy 2 Exz Fyz Gx Hy Kz L 0
 Từ Đại số tuyến tính, để vẽ mặt bậc hai: 
 1) Đưa dạng toàn phương (màu đỏ) về dạng chính tắc bằng biến đổi 
 trực giao. 
 2) Tìm phép biến đổi, xác định trục tọa độ mới. 
 3) Vẽ hình. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 8 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 2 2
 Xét đồ thị của hàm số: = + 
 2 2
 Tập hợp tất cả các điểm ( , ) của miền xác định , sao cho: 
 , = được gọi là đường mức, trong đó là hằng số cho trước. 
 k = 0 
 k = 1 
 k = 2 
 k = 3 
 k = 4 
 TS. Nguyễn Văn Quang 
 02-Feb-21 9 
 Đại học Công nghệ - ĐHQGHN 
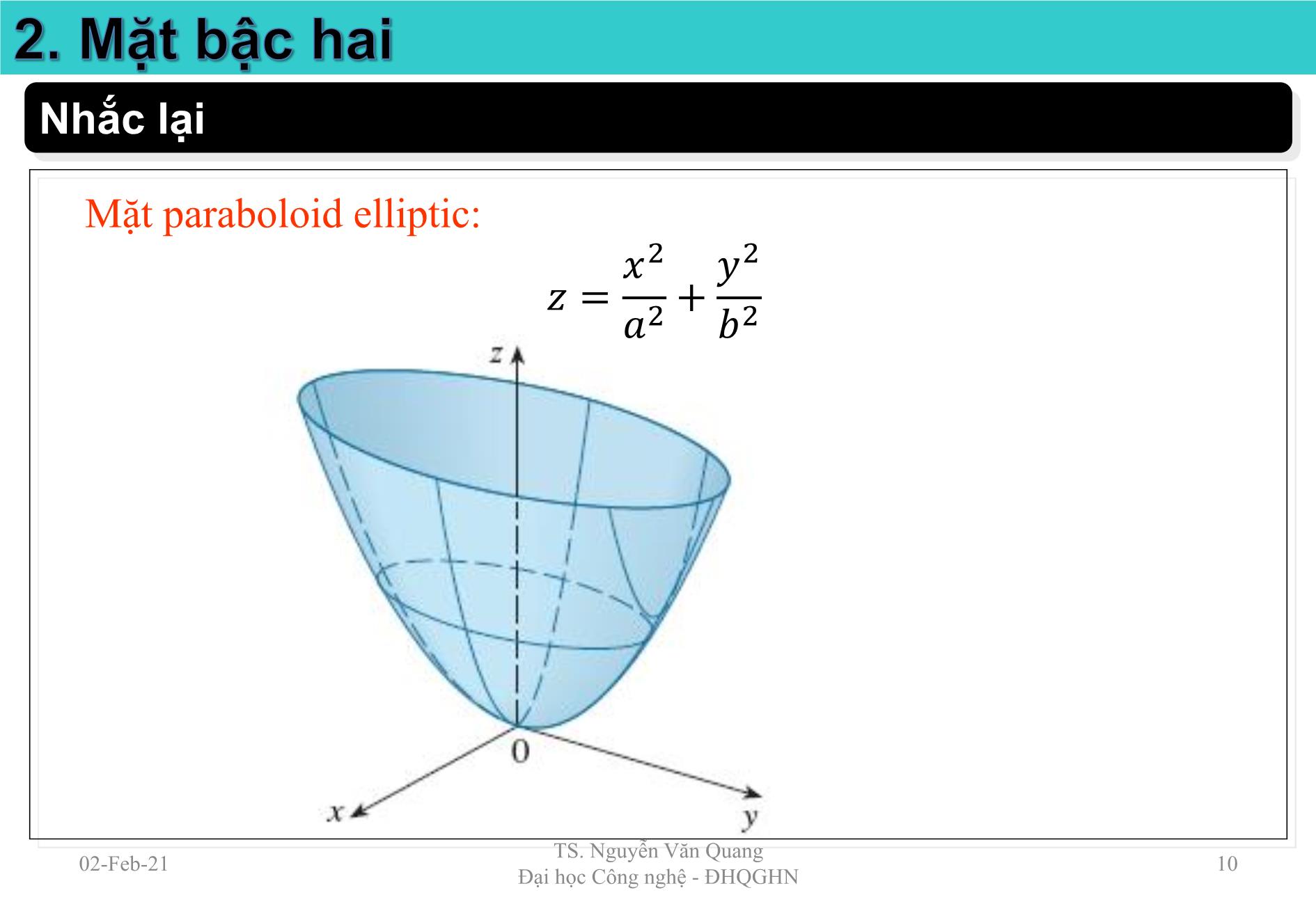
Nhắc lại 
 Mặt paraboloid elliptic: 
 2 2
 = + 
 2 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 10 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt paraboloid elliptic: = ( − 1)2+( − 3)2+4 
 TS. Nguyễn Văn Quang 
 02-Feb-21 11 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt paraboloid elliptic: = 2 + 2 
 TS. Nguyễn Văn Quang 
 02-Feb-21 12 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt ellipsoid: 
 2 2 2
 + + = 1 
 2 2 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 13 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt nón hai phía: 
 2 2 2
 + = 
 2 2 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 14 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Xét đồ thị của hàm số: 2 + 2 = 1. 
 Ta thấy với mọi , đường mức luôn là đường tròn bán kính bằng 1. 
 k = 2 
 k = 1 
 k = 0 
 k = -1 
 k = -2 
 TS. Nguyễn Văn Quang 
 02-Feb-21 15 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt trụ: trong phương trình thiếu hoặc , hoặc , hoặc . 
 2 2
 + = 1 
 2 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 16 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt trụ: 2 + 2 = 4 
 TS. Nguyễn Văn Quang 
 02-Feb-21 17 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt trụ: = 2 
 z 
 x 
 TS. Nguyễn Văn Quang 
 02-Feb-21 18 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt trụ: = 2 
 TS. Nguyễn Văn Quang 
 02-Feb-21 19 
 Đại học Công nghệ - ĐHQGHN 
Nhắc lại 
 Mặt trụ: = 2 − 2 
 TS. Nguyễn Văn Quang 
 02-Feb-21 20 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Cho 2 hàm số , , ( , ) hãy xét các giá trị của nó khi ( , ) tiến 
 tới (0, 0). 
 sin⁡( 2 + 2)
 , = 
 2 + 2
 2 − 2
 , = 
 2 + 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 21 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 sin⁡( 2 + 2)
 , = 
 2 + 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 22 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 2 − 2
 , = 
 2 + 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 23 
 Đại học Công nghệ - ĐHQGHN 
Nhận xét 
 • , , , đều không xác định tại (0,0). 
 • Khi , dần đến (0,0): các giá trị của ( , ) dần tới 1, các giá 
 trị của ( , ) không tiến tới bất kỳ một giá trị nào. 
 • Dự đoán: 
 sin⁡( 2+ 2)
 lim = 1. 
 ( , )→(0,0) 2+ 2
 2− 2
 lim không tồn tại. 
 ( , )→(0,0) 2+ 2
 TS. Nguyễn Văn Quang 
 02-Feb-21 24 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa giới hạn kép 
 2
 Cho hàm hai biến = , , 0( 0, 0) ∈ 푅 sao cho 0 là điểm tụ 
 của . 
  Ta nói giới hạn của hàm khi ( , ) dần đến điểm 0 bằng , nếu: 
 x,,, y D  x y f x y  a
 n n fnn 00 n n 
 Ký hiệu của giới hạn (kép): limf ( x , y ) a
 (,)(,)x y x00 y
 22
    0,  0:(,)xyDxyf ,(,)(,),( xy0 0 xx 0 ) ( yy 0 ) 
 Khi đó: f(,). x y a 
 limf ( x , y ) a
 Ký hiệu khác của giới hạn (kép): xx 0
 yy 0
 TS. Nguyễn Văn Quang 
 02-Feb-21 25 
 Đại học Công nghệ - ĐHQGHN 
Tính chất của giới hạn 
 1. lim [f ( x , y ) g ( x , y )] lim f lim g
 (,)(,)(,)(,)(,)(,)xyab xyab xyab 
 2. lim [f ( x , y ) g ( x , y )] lim f  lim g
 (,)(,)(,)(,)(,)(,)xyab xyab xyab 
 limf ( x , y )
 f(,) x y
 3. lim (,)(,)x y a b , neu limg 0
 (,)(,)(,)(,)x y a bg( x , y ) lim g ( x , y ) x y a b
 (,)(,)x y a b
 4. Neu f ( x , y ) g ( x , y ) h ( x , y ) va
 limf lim h M , thì lim g M .
 (,)(,)(,)(,)(,)(,)xyab xyab xyab 
 TS. Nguyễn Văn Quang 
 02-Feb-21 26 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn nếu tồn tại hoặc chứng minh không tồn tại: 
 1
 I lim x y sin
 (xy , ) (0,0) x
 11
 0 |f ( x , y ) | x y sin | x | y sin | x | y
 xx
 0 
 1
 lim xy sin 0.
 (xy , ) (0,0) x
 TS. Nguyễn Văn Quang 
 02-Feb-21 27 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn nếu tồn tại, hoặc chứng tỏ giới hạn không tồn tại: 
 3xy2
 I lim
 (xy , ) (0,0) xy22 
 3x22 y x
 0 |f ( x , y ) | 3| y |, vì 1.
 x2 y 2 x 2 y 2
 0 
 3xy2
 lim 0.
 (xy , ) (0,0) xy22 
 TS. Nguyễn Văn Quang 
 02-Feb-21 28 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn: 
 lim 
 ( , )→(0,0) 2 + 2
 Dọc theo trục : y 
 0
 lim = lim = 0 
 ( , )→(0,0) 2 + 2 ( , )→(0,0) 2
 Dọc theo trục = : 
 2 1 x 
 lim = lim = 
 ( , )→(0,0) 2 + 2 ( , )→(0,0) 2 2 2
 Do đó: không tồn tại giới hạn (kép). 
 TS. Nguyễn Văn Quang 
 02-Feb-21 29 
 Đại học Công nghệ - ĐHQGHN 
Chú ý 
 Nếu ( , ) tiến tới ( , )⁡theo ít nhất 2 cách khác nhau, mà giá trị 
 hàm ( , ) dần tới các giới hạn khác nhau thì: 
 lim ( , ) 
 ( , )→( , )
 không tồn tại. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 30 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn (nếu có) hoặc chứng tỏ không tồn tại: 
 xy22 2
 I lim
 (xy , ) (0,0) xy22 
 1 n 1
 Chọn dãy (xy nn , ) ,0  (0,0) . Khi đó: f( xnn , y ) f ,0 1
 n n
 1 n 
 Chọn dãy thứ hai ( xynn , ) 0,  (0,0)
 n
 1
 Khi đó f( xnn , y ) f 0, 2.
 n
 Vậy tồn tại hai dãy dần đến (0,0) nhưng giá trị của tại những điểm 
 đó tiến đến hai số khác nhau, suy ra không tồn tại giới hạn đã cho. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 31 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn (nếu có) hoặc chứng tỏ không tồn tại: 
 xy
 I lim
 (xy , ) (0,0) xy22 
 Chọn = , khi đó: 
 , = , = 
 1 + 2
 , là một đại lượng phụ thuộc vào , mà thay đổi nên không 
 tồn tại giới hạn. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 32 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn (nếu có) hoặc chứng tỏ không tồn tại: 
 xy3
 I lim
 (xy , ) (0,0) xy26 
 1 n 1
 Chọn dãy (xy nn , ) ,0  (0,0) . Khi đó: f( xnn , y ) f ,0 0.
 n n
 11 n 
 Chọn dãy thứ hai (xynn , ) ,  (0,0)
 n3 n
 1 1 1
 Khi đó f(,),. xnn y f 
 n3 n 2
 Vậy tồn tại hai dãy dần đến (0,0) nhưng giá trị của tại những điểm 
 đó tiến đến hai số khác nhau, suy ra không tồn tại giới hạn đã cho. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 33 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn (nếu có) hoặc chứng tỏ không tồn tại: 
 xy22
 I lim
 (xy , ) (0,0) x2 y 2 () x y 2
 1 n 1
 Chọn dãy (xy nn , ) ,0  (0,0) . Khi đó: f( xnn , y ) f ,0 0.
 n n
 11 n 
 Chọn dãy thứ hai (xynn , ) ,  (0,0)
 nn
 11
 Khi đó f( xnn , y ) f , 1.
 nn
 Vậy tồn tại hai dãy dần đến (0,0) nhưng giá trị của f tại những điểm đó 
 tiến đến hai số khác nhau, suy ra không tồn tại giới hạn đã cho. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 34 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn (nếu có) hoặc chứng tỏ không tồn tại: 
 xy
 I lim
 (xy , ) (0,0)11 3 xy
 Đặt 푡 = , khi đó ( , ) → (0,0) thì 푡 → 0: 
 푡
 = lim = −3 
 푡→0 1 − 3 1 + 푡
 TS. Nguyễn Văn Quang 
 02-Feb-21 35 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm giới hạn (nếu có) hoặc chứng tỏ không tồn tại: 
 xy2 
 I lim
 (xy , ) (0,0) xy2 93 
 Đặt 푡 = 2 + , khi đó ( , ) → (0,0) thì 푡 → 0: 
 푡
 = lim = 6 
 푡→0 푡 + 9 − 3
 TS. Nguyễn Văn Quang 
 02-Feb-21 36 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa 
 Hàm số ( , ) được gọi là liên tục tại ( 0, 0), nếu: 
 lim ( , ) = ( 0, 0) 
 ( , )→( 0, 0)
 Hàm được gọi là liên tục trên miền nếu nó liên tục tại mọi điểm trên 
 miền . 
 Tổng, hiệu, tích của hai hàm liên tục là hàm liên tục. 
 Thương của hai hàm liên tục là hàm liên tục (nếu hàm ở mẫu khác 0). 
 Hàm hợp của hai hàm liên tục là hàm liên tục (tại những điểm thích 
 hợp). 
 TS. Nguyễn Văn Quang 
 02-Feb-21 37 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa 
 Các hàm sau đây được gọi là hàm sơ cấp cơ bản: 
 1) Hàm mũ; 2) Hàm lũy thừa; 3) Hàm lượng giác; 4) Hàm lượng 
 giác ngược; 5) Hàm logarit; 6) Hàm hằng. 
 Hàm thu được từ các hàm sơ cấp cơ bản bằng hữu hạn các phép 
 toán: cộng, trừ, nhân, chia, lấy hàm hợp được gọi là hàm sơ cấp. 
 Các phép toán: cộng, trừ, nhân, chia, lấy hàm hợp các hàm sơ cấp 
 là hàm sơ cấp. 
 Định lý 
 Hàm sơ cấp liên tục trên tập xác định. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 38 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Khảo sát tính liên tục của hàm sau 푅2: 
 sin(xy33 )
 , (xy , ) (0,0)
 f(,) x y xy22 
 0, (xy , ) (0,0)
 sin(x33 y ) sin t sin(x3 y 3 ) sin( x 3 y 3 ) x 3 y 3
  t 0 1 
 xy33 t x2 y 2 x 3 y 3 x 2 y 2
 xy33 
 0 |xy | | |
 22 limf ( x , y ) 1.0 0 f (0,0)
 xy (xy , ) (0,0)
 Suy ra liên tục tại (0,0). Vậy hàm đã cho liên tục trên 푅2. 
 TS. Nguyễn Văn Quang 
 02-Feb-21 39 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tìm tất cả các giá trị của để hàm số liên tục tại điểm (0,0): 
 xy22 
 , (xy , ) (0,0)
 f(,) x y xy22 
 a, ( x , y ) (0,0)
 Ta có lim f ( x , y ) không tồn tại. 
 (xy , ) (0,0)
 Vậy hàm không liên tục tại (0,0). Không tồn tại . 
 TS. Nguyễn Văn Quang 
 02-Feb-21 40 
 Đại học Công nghệ - ĐHQGHN