Bài giảng Cơ sở truyền số liệu - Chương 1: Lý thuyết xếp hàng và ứng dụng
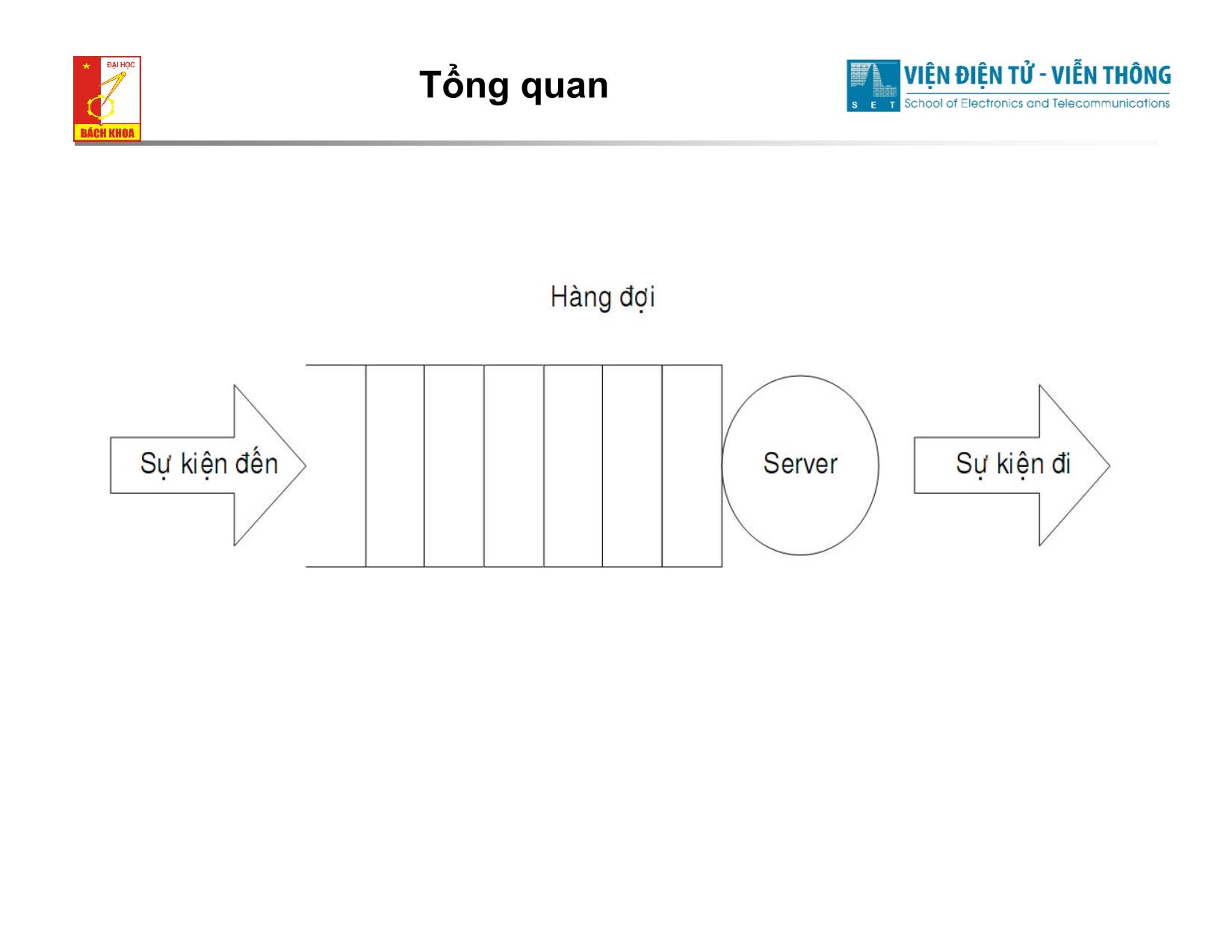
Trong các hệ thống dịch vụ, chủ thể phục vụ (server)
lần lượt phục vụ các đối tượng sử dụng dịch vụ. Số
lượng chủ thể có thể nhiều hơn 1
• Ví dụ:
– Các hệ thống điện thoại: khi số lượng lớn khách hàng
quay số để kết nối đến một trong những đường ra hữu
hạn của tổng đài.
– Trong mạng máy tính: khi mà gói tin được chuyển từ
nguồn tới đích và đi qua một số lượng các nút trung
gian. Hệ thống hàng đợi xuất hiện tại mỗi nút ở quá
trình lưu tạm thông tin tại bộ đệm.

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cơ sở truyền số liệu - Chương 1: Lý thuyết xếp hàng và ứng dụng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cơ sở truyền số liệu - Chương 1: Lý thuyết xếp hàng và ứng dụng

ào không (yêu
cầu dịch vụ, mức độ ưu tiên...)?
• Miêu tả của tiến trình đến (phân bố khoảng thời
gian đến)
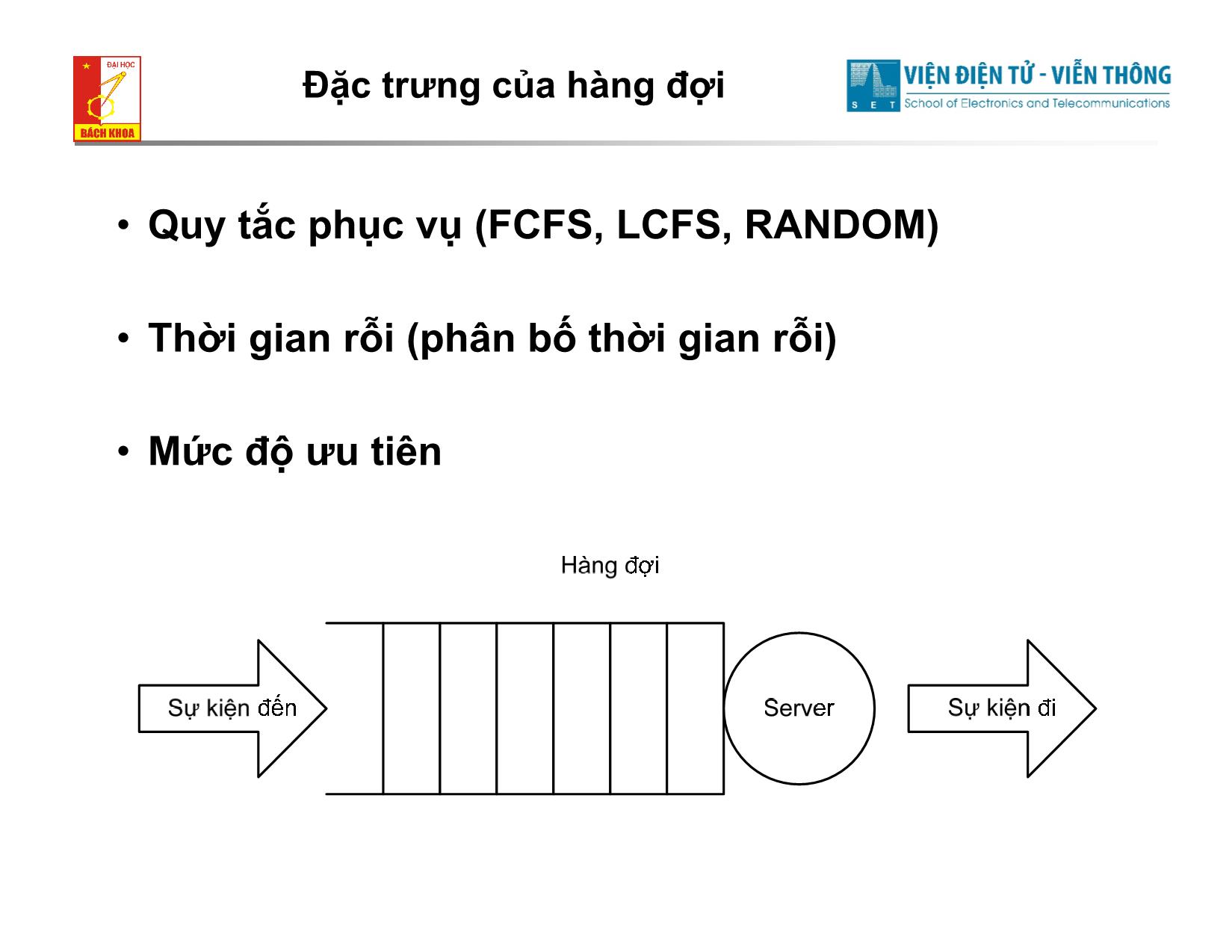
Đặc trưng của hàng đợi
• Quy tắc phục vụ (FCFS, LCFS, RANDOM)
• Thời gian rỗi (phân bố thời gian rỗi)
• Mức độ ưu tiên
Phân tích hệ thống hàng đợi
• Phân tích giải tích
• Quá trình mô phỏng
• Cả hai phương pháp trên
Kết quả phân tích
(về phía khách hàng)
• Thời gian xếp hàng (trễ hàng đợi)
• Tổng trễ (bao gồm trễ hàng đợi và trễ phục vụ )
• Số lượng khách hàng trong hàng đợi
• Số lượng khách hàng trong hệ thống (gồm khách
hàng chờ và khách hàng đang được phục vụ )
• Xác suất nghẽn mạng (khi kích thước bộ đệm hữu
hạn)
Kết quả phân tích
về phía hệ người phục vụ
• Khả năng sử dụng server
• Khả năng sử dụng bộ đệm
• Lợi ích thu được (thông số dịch vụ và các xem xét
về kinh tế)
• Lợi ích bị mất (thông số dịch vụ và các xem xét về
kinh tế)
Phân tích hàng đợi
λ - tốc độ đến trung bình , thời gian đến trung bình -1/λ
µ - tốc độ phục vụ trung bình, thời gian phục vụ trung bình 1/µ
Với kích thước của bộ đệm là vô hạn, quy tắc phục vụ là FCFS
Phân tích hàng đợi
t
Phân tích hàng đợi
• Sự kiện A: có 1 sự đến trong Δt
• Sự kiện B: không có sự đến nào trong Δt
• Sự kiện C: có nhiều hơn 1 sự đến trong Δt
• Giả sử rằng Δt →0. Như vậy ta sẽ có:
Pr{A}= λ ∆t
Pr{B}= 1- λ ∆t
Giả thiết Pr{C}= 0
• Số lượng sự kiện đến tuân theo phân bố Poisson
Phân tích hàng đợi
• Định nghĩa luật phân bố Poisson*
e λλn
P(N=n)= (n=0,1,2,...)
n!
• Đồng thời, khoảng thời gian đến (được tính giữa hai
sự đến liên tiếp) tuân theo luật phân bố mũ* với
tham số λ
(*) Trong MS Excel có hàm POISSON và hàm
a(t) = λe-λt
EXPONDIST
Phân tích hàng đợi
Phân tích hàng đợi
• Sự kiện A: có 1 sự kiện đi trong ∆t
• Sự kiện B: không có sự kiện đi nào trong ∆t
• Sự kiện C: có nhiều hơn 1 sự kiện đi trong ∆t
• Giả sử ∆t →0. Như vậy ta sẽ có:
Pr{A}= µΔt
Pr{B}= 1- µΔt
• D là sự kiện của 1 hoặc nhiều sự đến AND với sự kiện
của 1 hoặc nhiều sự đi trong khoảng Δt. Giả sử Pr{D}=0
Phân tích hàng đợi
• Định nghĩa pN(t) là xác xuất mà hệ thống có N
khách hàng tại thời điểm t
•Khi đó có:
p0(t+∆t )= p0(t)(1-λ∆t)+p1(t)µ∆t, N=0
pN(t+∆t )= pN(t)(1-λ ∆t-µ∆t)+pN-1(t)λ∆t+ pN+1(t)µ∆t,
N>0
Ở thời điểm t+∆t có N khách hành nếu ở t có N khách hàng và
không có sự đến/ sự đi...
Phân tích hàng đợi
•Từ đó suy ra:
dp (t)
0 = λp (t)+ μp (t), N = 0
dt 0 1
dp (t)
N = (λ+ μ)p (t)+ λp (t)+ μp (t), N > 0
dt N N 1 N+1
Phân tích hàng đợi
• Ở điều kiện ổn định, khi t→∞, ta có
dp (t)
0 = 0, N = 0
dt
dp (t)
N = 0, N > 0
dt
•Hay: p0(t)=p0, với N=0
pN(t)=pN, với N>0
Tức là xác xuất hệ thống rơi vào một trạng thái
nào đó không phụ thuộc thời gian nữa...
Phân tích hàng đợi
•Hệ phương trình vi phân trở thành (đặt ρ=λ /µ < 1):
p1=ρp0
N+1
pN+1(t)=(1+ρ)pN- ρpN-1=ρpN=ρ p0, N>0
• Theo điều kiện phân bố chuẩn:
pi(t)=1,t 0
i
•Suy ra:
i
pi = ρ (1-ρ ), i=0,1,
Số lượng khách hàng trung bình
• Xét trong một khoảng thời gian đủ lớn, số lượng khách
hàng lưu trong hệ thống được tính theo công thức:
i ρ
E[N]=ipi =iρ (1 ρ)=
i=0 i=0 1 ρ
* Để chứng minh, tách thành 2 tổng rồi thay thế
i+1 sang i để rút gọn...
Số lượng trung bình
• Số lượng khách hàng lưu trong hàng đợi được tính bằng:
ρ ρ ρ2
E[NQ ]=(i 1)pi =ipi pi = (1 p0 )= ρ=
i=1 i=1 i=1 1 ρ 1 ρ 1 ρ
* Tổng xuất phát từ i = 1, nghĩa là công thức chỉ
đúng khi có ít nhất một khách hàng trong hệ thống
Thời gian trung bình
• Thời gian một khách hàng lưu lại trong hệ thống bao
gồm:
•Thời gian chờ xếp hàng
•Thời gian phục vụ
Thời gian trung bình
• Giả thiết:
•Hệ thống ở trạng thái ổn định tức λ ≤ μ
•Quy tắc phục vụ là FCFS
Thời gian trung bình
• Tổng thời gian lưu trong hệ thống:
k 1 k+1 1
EW = pk + pk = pk =
k=0 μ k=0 μ k=0 μ μ(1 ρ)
Thời gian trung bình
• Tổng thời chờ trong hàng đợi:
k ρ
E W Q = p k =
k = 0 μ μ( 1 ρ)
1 1 1 ρ
EW = EW = =
Q μ μ(1 ρ) μ μ(1 ρ)
Xác suất để khách hàng phải đợi
• Sự kiện một khách hàng đến phải đợi chính là khi trong
hệ thống có ít nhất 1 khách hàng:
Pwait = 1 – p0 = ρ
• Đây cũng chính là xác suất hệ thống ở trạng thái bận Pbusy
Tiến trình điểm và tính chất Markov
• Tính dừng (stationary-time). Diễn tiến của các sự kiện trong một
khoảng thời gian không phụ thuộc vào thời điểm bắt đầu quan sát.
Xác suất có k cuộc gọi đến trong khoảng thời gian [t1, t1+t2] là độc
lập với t1, nghĩa là với mọi t, k ta có:
p (Nt1+t2 Nt1 )=k = p (Nt1+t2+t Nt1+t )=k
• Tính độc lập (independence) hay còn gọi là tính không nhớ. Trạng
thái tiếp theo chỉ phụ thuộc vào trạng thái hiện tại, nhưng độc lập
với việc nó đã có được như thế nào. Đây chính là đặc tính của tiến
trình Markov
p (Nt2 Nt1)=k|Nt1 Nt0=n =p (Nt2 Nt1)=k
Tiến trình điểm và tính chất Markov
• Tính đều đặn (regularity). Xác suất xảy ra với nhiều hơn một sự
kiện ở cùng một thời điểm bằng không:
p (N t+ Δt N t ) 2 = o Δt ; khi : Δt 0, o( Δt ) 0
• Một ví dụ điển hình của tiến trình điểm là tiến trình tuân theo luật
Poisson. Xác suất để có k sự kiện trong khoảng thời gian T:
λT k e λT
p(k) =
k!
•Phân bố chuẩn: p(k) = 1
k = 0
•Kỳ vọng:
E(k) = kp(k) = λT
k=0
Đính lý Little
Tính trung bình, số lượng khách hàng nằm trong hệ thống
được tính bằng tích của tốc độ đến và thời gian phục vụ
• Ký hiệu:
•N(t): số lượng khách hàng nằm trong hệ thống tại thời điểm t
•: số lượng khách hàng đến hệ thống khoảng thời gian (0,t)
α t
•: số lượng khách hàng rời khỏi hệ thống trong (0,t)
βt
•: thời gian chiếm dùng của khách hàng i
T i
Đính lý Little
• Đẳng thức sau đây đúng vì 2 vế đều biểu diễn diện tích phần màu
xanh: t α t
N t = T
i
0 i = 1
α
• Tương đương với: t
T
1 t α i
N t = t i= 1 dpcm
t 0 t α t
Quá trình sinh tử
• Trong đó λ i , μ i là tốc độ sự kiện đến và đi xét tại trạng thái i
• Với một hệ thống dừng và ổn định thì tổng các dòng đi vào một
trạng thái bằng tổng các dòng đi ra
Các mô hình hàng đợi: ký hiệu
kendal
• Ký hiệu tổng quát cho một hệ thống hàng đợi:
A/S/c/B/R/SD
• A: mô tả tiến trình đến, thường quan tâm đến khoảng thời gian giữa
hai lần đến liên tiếp:
•M: Tiến trình mũ (là tiến trình Markov hay tiến trình không
nhớ). Tức trạng thái tiếp theo chỉ phụ thuộc vào trạng thái hiện
tại, nhưng độc lập với việc nó đã có được như thế nào
•Er: Tiến trình Erlang bậc r
•Hr: Tiến trình siêu số mũ bậc r
•D: Tiến trình tất định (deterministic)
Các mô hình hàng đợi: ký hiệu
kendal
• S: mô tả tiến trình phục vụ, thường quan tâm đến khoảng thời
gian cần thiết để phục vụ mỗi sự đến. Cũng có thể tuân theo 1 số
luật như đối với tiến trình đến
• c: Số lượng server
• B: Kích thước bộ đệm. Đôi khi kí hiệu này bao gồm cả sự kiện
đang được phục vụ
• R: Số nguồn phát ra sự kiện. Nếu các nguồn là tiến trình Markov
thì tổng hợp của chúng cũng là 1 tiến trình Markov với:
λ= ∑ λ i
• SD: Quy tắc phục vụ
• Ví dụ : M/M/c/∞
Hàng đợi M/M/1/∞
• Tiến trình đến và tiến trình phục vụ có thuộc tính Markov. Thời
gian giữa hai lần đến và thời gian phục vụ tuân theo phân bố mũ
• Hệ thống có 1 server, dung lượng đệm là vô hạn
• Mật độ lưu lượng: ρ= λ
μ
ρ
• Số lượng khách hàng trung bình trong hệ thống: L=
1 ρ
• Số lượng khách hàng trung bình trong server:
Ls = P N 1 =1 P N = 0 =1 1 ρ = ρ
Hàng đợi M/M/1/∞
• Số lượng khách hàng trung bình trong hàng đợi:
2
ρ ρ
L =L− L = − ρ=
q s
1 − ρ 1 − ρ
• Thời gian trung bình lưu trong hệ thống của mỗi khách hàng:
L ρ 1
W = = =
λ λ 1 ρ μ λ 1 ρ
• Thời gian phục vụ trung bình cho mỗi khách hàng: Ws = =
2 μ λ
• Thời gian đợi trung bình: ρ
Wq =W Ws =
λ 1 ρ
Hàng đợi M/M/1/∞
• Ví dụ: một luồng gói đến một thiết bị chuyển mạch gói
với tốc độ trung bình là 180 packets/minute. Chiều dài
gói trung bình là 1000 byte. Tốc độ của dòng số đầu ra là
20000byte/s. Giả thiết dung lượng đệm là đủ lớn. Hãy
tính thời gian trễ trung bình tại hệ thống, số bản tin trung
bình trong mỗi hệ thống, chiều dài hàng đợi và thời gian
đợi trung bình.
Hàng đợi M/M/1/∞
λ= 240 =4
• Tốc độ đến: 60
500
• Thời gian phục vụ trung bình: μ= =5
100
λ 4
ρ= = =0.8
• Mật độ lưu lượng: μ 5
ρ 0.8
• Số bản tin trong hệ thống L: = =4
1− ρ 1− 0.8
L 4
• Thời gian trong hệ thống: = =1
λ 4
2
• Chiều dài hàng đợi: ρ 0,8.0,8
= =3,2
1− ρ 1− 0,8
• Thời gian đợi trung bình: ρ2 L 3,2
= q = =0,8
λ(1 ρ) λ 4
Hàng đợi M/M/1/K
λp0 =μp1 ;n 1,...,K 1
λpn 1+μpn+1 =(λ+μ)pn
λpK 1 =μpK;n=K
* K đã bao gồm khách hàng đang được phục vụ
Hàng đợi M/M/1/K
n
• Do đó: pn =ρ p0;n 0,K
K
• Mặt khác, cũng có:
∑ pn=1
n= 0
• Nên:
1 1 ρ
p = =
0 K 1 ρK+1
ρn
n=0
và:
1 − ρ n
pn = × ρ
1 − ρ K+ 1
Hàng đợi M/M/1/K
• Xác suất để một yêu cầu bị từ chối:
1− ρ K
Ploss =pK= × ρ
1− ρ K+ 1
• Số sự kiện trung bình lưu trong hệ thống:
K K
1 − ρ n
N= ∑ npn= K+ 1 × ∑ nρ
n= 1 1− ρ n= 1
• Để ý:
K K+ 1 K 1 (K+1)ρK+KρK+1
n 1− ρ f'(ρ) nρn 1=
f ρ = ∑ ρ = 2
n= 0 1− ρ n=1 (1 ρ)
• Cuối cùng:
K 1
N (K 1)
1 1 K 1
Hàng đợi M/M/1/K
• Khi : thì: p = p và: 1
ρ 1 n 0 pn =
K K+1
• Mặt khác, cũng có:
∑ pn=1
n= 0
• Suy ra:
K K
N npn
n 1 2
• Số sự kiện trung bình trong hàng đợi:
K K K
Nq =(n 1)pn =npn pn =N (1 p0 )
• Hay: n=1 n=1 n=1
1 ρ (K+1)ρK+1
N = +
q 1 ρ 1 ρK+1
Hàng đợi M/M/1/K
• Thời gian đợi trung bình được tính:
1 1 1 1 k
E Wq = E N kpk = kpk
μ1 pk μ1 pk 2
• Thời gian lưu trong hệ thống trung bình:
E N k
E W = =
λ 2λ
Hàng đợi M/G/1/∞
• Tiến trình đến Markov, tham số λ
• Tiến trình phục vụ là bất kỳ
• Chiều dài hàng đợi không giới hạn
• Số sự kiện trung bình trong hệ thống:
2 2 2 2 2 2
2ρ ρ +λ σy ρ +λ σy
E N = =ρ+ 1
2 1 ρ 2 1 ρ
1
2 y=
• Trong đó σ y là phương sai của biến ngẫu nhiên
μ
• Thời gian trung bình lưu lại trong hệ thống:
2
1 ρ+ λμσ y N
E W = + = E 2
μ 2μ 1 ρ λ
Trang web môn học
• https://sites.google.com/site/fetphamvantien/home
/fund-data-net
• Bài tập dài và hướng dẫn đã được tải lên
Hàng đợi M/D/1/∞
• Tiến trình đến Markov, tham số λ
2
• Tiến trình phục vụ là bất biến, tức σ y = 0
• Từ (1) và (2) trong hàng đợi M/G/1 suy ra số sự kiện :
2 ρ 2 ρ
E N D = E N |σy =0 =
2 1 ρ
• Số sự kiện trung bình trong hàng đợi:
ρ 2
E N = E N ρ =
q D 2 1 ρ
• Thời gian trung bình lưu lại trong hệ thống:
E N 2 ρ
E W = =
D λ 2μ 1 ρ
Hàng đợi M/D/1/∞
• Thời gian đợi trung bình:
1 ρ
E Wq = E W =
D μ 2μ 1 ρ
Hàng đợi M/M/c/∞
• Tốc độ đến của các sự kiện là λ
• Tốc độ phục vụ của các server là μ i với i = 1, 2,...,c. Để đơn
giản, giả thiết
μ1 = μ 2 = μ 3=...= μ c = μ
λ
• Mật độ lưu lượng : ρ=
• Giả thiết thứ tự phục vụ của cáccμ server là từ 1, 2, 3,...,c
• Trong sơ đồ sinh-tử ?
HàngHàng đợ đợi M/M/c/0i M/M/c/∞
• Hệ phương trình cân bằng chuyển đổi trạng thái:
λp0 = μp1
λpn 1 +(n+1)μμn+1 = (λ+ nμμ)n ;n 1,...,c 1
λpn 1 + cμμn+1 = (λ+ cμμ)n ;n > c 1
p = 1
n
n=0
Hàng đợi M/M/c/∞
λ
• Đặt a= =cρ
μ
• Xác suất để có n sự kiện trong hệ thống
1
p = a n p với n < c
n n! 0
c
a n− c
p = ρ p với n >= c
n c! 0
• Tương tự như hàng đợi M/M/1/∞ ta có:
c 1 c
n 1 a 1
p 0 = [ a + ]
n= 0 n! c! ( 1 ρ)
Hàng đợi M/M/c/∞
• Xác suất để một yêu cầu phải đợi (công thức Erlang C):
c 1 c
p0 a
p{Wq > 0} = p{N>=c} = pq = 1 p =
n c! (1 ρ)
n=0
• Hay:
c c 1 c
a n 1 a 1
pq = [ a + ]
c!(1 ρ) n=0 n! c!(1 ρ)
Hàng đợi M/M/c/∞
• Chiều dài hàng đợi trung bình:
ρ
E Nq = n c pn = pq
n=c 1 ρ
• Số yêu cầu đang được phục vụ trung bình:
c λ
E Ns = npn + cpn = = a
n=0 n=c+1 μ
• Xác suất để thời gian đợi không lớn hơn giá trị t là:
μ c a t
P W q t= 1 p q e
Hàng đợi M/M/c/∞
• Thời gian đợi trung bình:
1 1 1
E W = E N = p
q λ q cμ 1 ρ q
• Số yêu cầu trung bình trong hệ thống:
ρ
E N = E N +E N = p +a
q s 1 ρ q
• Thời gian lưu lại trung bình trong hệ thống:
1
E W = E N
λ
Hàng đợi M/M/c/0
• Tốc độ đến của các sự kiện là λ
• Tốc độ phục vụ của các server là μ i với i = 1, 2,...,c. Để đơn
giản, giả thiết
μ1 = μ 2 = μ 3=...= μ c = μ
• Giả thiết thứ tự phục vụ của các server là từ 1, 2, 3,...,c
• Sơ đồ quá trình sinh-tử ?
Hàng đợi M/M/c/0
• Hệ phương trình cân bằng chuyển đổi trạng thái:
λp0 = μp1 ;n 1,...,c 1
λpn 1 +(n+1)μμn+1 = (λ+ nμμ)n
λpc 1 = cμμc ;
c
p = 1
n
n=0
Hàng đợi M/M/c/0
λ
• Đặt a= =cρ
μ
• Xác suất để có n sự kiện trong hệ thống
1
p = a n p với n <= c
n n! 0
• Xác suất để một yêu cầu nào đó đến bị từ chối
c c i
ρ ρ − 1
pc = [ ∑ ]
c! i= 0 i!
Đây chính là công thức Erlange B
Công thức Erlang
• Công thức Erlang C cho biết xác suất để một yêu cầu đến phải chờ
trong hàng đợi:
c c 1 c
a n 1 a 1
p q = [ a + ]
c! ( 1 ρ) n= 0 n! c! ( 1 ρ)
• Xác suất để một yêu cầu phải chờ trong khoảng thời gian t trước
khi được phục vụ:
μ(c a)t
P W q t= 1 p q e
• Công thức Erlang B cho biết xác suất một yêu cầu đến bị từ chối
phục vụ ngay:
c c i
ρ ρ 1
p c = [ ]
c! i= 0 i!
Cường độ lưu lượng
• Lưu lượng phát sinh từ một người dùng (thời gian chiếm dùng H)
Au = λu .H
• Lưu lượng phát sinh tổng cộng từ nhiều nguồn tổng hợp lại:
A= λ.H
• Lưu lượng mang (không vượt quá số kênh) là giá trị lưu lượng
Ac
thực tế được phục vụ
• Lưu lượng tổn thất là hiệu số giữa lưu lượng phát sinh và lưu lượng
mang
Al = A Ac
• Đơn vị đo lưu lượng là Erlang, thường tính theo giờ
Cường độ lưu lượng
• Ví dụ: một người dùng có tốc độ phát sinh cuộc gọi là 3 cuộc/giờ,
thời gian chiếm kênh trung bình là 10 phút. Vậy tải phát sinh từ
người dùng này là (30x10)/60 = 0,5Er
• Nếu có 100 người dùng như vậy thì lưu lượng phát sinh tổng cộng
?
A= λ.H =100x0,5= 50Er
Bậc phục vụ (GoS)
• Hệ thống không hàng đợi (M/M/c/0) (blocked calls cleared):
•Cuộc nối bị từ chối khi tất cả các kênh phục vụ đều bận
•GoS được đánh giá qua công thức Erlang B
A c c A i
p(blocking ) = [ ] 1
c! i= 0 i!
Grade of Service (GoS)
Bậc phục vụ (GoS)
• Hệ thống có hàng đợi M/M/c/∞ (blocked calls delayed)
•GoS được tính bằng xác suất một cuộc gọi phải chờ lâu hơn một
khoảng thời gian chờ nào đó
•Sử dụng công thưc Erlang C để đánh giá
Ac
p(delay > 0 )=
c 1 1
Ac + c!(1 A / c) An
n=0 n!
c A
t
p(delay > t) = p(delay > 0 )e H
CBườậcng ph độục vlụư u(GoS) lượ ng
• Ví dụ: Cho hệ thống trễ có tốc độ cuộc gọi là 10 cuộc/giờ, thời gian
chiếm kênh mỗi cuộc là 4 phút, số kênh phục vụ là 3. Tính lưu
lượng phát sinh. Xác suất để một để một cuộc gọi phải vào hàng
đợi, xác suất để được phục vụ ngay là bao nhiêu ?
sssdsds
ĐS: 4/9
Bậc phục vụ (GoS)
ĐS: 4/9
ĐS: 4/9
Tham khảo (Erlang C)
ĐS: 4/9
Tham khảo (Erlang B)
ĐS: 4/9File đính kèm:
 bai_giang_co_so_truyen_so_lieu_chuong_1_ly_thuyet_xep_hang_v.pdf
bai_giang_co_so_truyen_so_lieu_chuong_1_ly_thuyet_xep_hang_v.pdf

