Xác định trường nhiệt độ trong kết cấu bê tông khối lớn thời kỳ đầu mới đổ

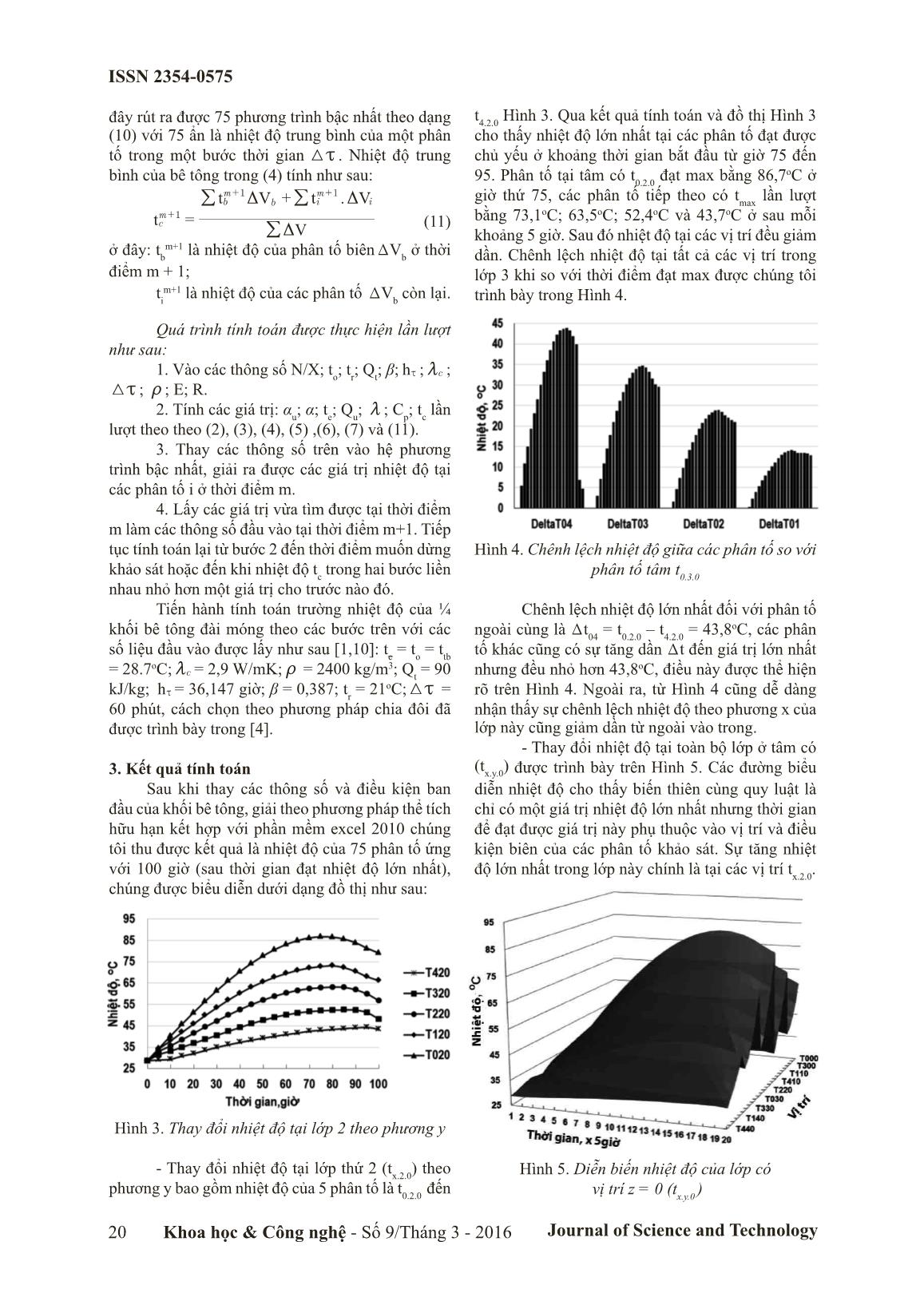
vậy sự phụ thuộc của hệ số dẫn nhiệt bê tông vào độ 
tuổi của bê tông trong quá trình đông cứng là chủ 
yếu và nó được biêu diễn bằng biểu thức:
 ma = cm (1,33 – 0,33.α) (6)
Trong đó:
ma : hệ số dẫn nhiệt của bê tông tại giá trị α 
(W/mK)
cm : hệ số dẫn nhiệt của bê tông khi đóng rắn 
hoàn toàn, W/mK
α: hệ số mức độ thủy hóa của xi măng. 
e. Nhiệt dung riêng
Khi các cốt liệu của bê tông nhận nhiệt do 
phản ứng thủy hóa sinh ra sẽ làm cho nhiệt dung 
riêng thay đổi. Tất nhiên, lượng nhiệt do thủy hóa 
sinh ra thay đổi theo thời gian và nó cũng là nguyên 
nhân làm cho giá trị nhiệt dung riêng C
p
 (kJ/kg.K) 
của bê tông thay đổi. Theo [6], giá trị nhiệt dung 
riêng của bê tông sau khi tính toán, thí nghiệm và 
biến đổi, các tác giả cũng đưa ra được biểu thức tính 
toán C
p
 của bê tông theo thời gian như sau:
C
pα
 = 1300(1,5 – 0,5α) (7)
Như vậy, các thông số nhiệt vật lý của bê 
tông khi đóng rắn đều thay đổi theo thời gian đông 
kết và được tính thông qua hệ số mức độ thủy hóa 
xi măng.
2.2. Mô hình vật lý của đối tượng nghiên cứu
 Để tiện tính toán và so sánh, chúng tôi sử 
dụng bê tông khối lớn dạng hình hộp được trình bày 
trong [1]. Khối bê tông đài móng có kích thước các 
cạnh lần lượt là 4,6#4,6#4m. Đây là khối mẫu 
được thi công để tiến hành thí nghiệm theo dõi diễn 
biến nhiệt độ và ứng suất trong khối bê tông, phục 
vụ thiết kế biện pháp thi công đài móng công trình 
Keangnam Hà Nội Landmark Tower. Chiều cao 
khối bê tông thí nghiệm (4m) đúng bằng chiều dày 
lớn nhất của đài móng.
Cấp phối bê tông của khối mẫu (Bảng 1) 
giống như cấp phối bê tông được thiết kế cho phần 
đài móng công trình sẽ thi công.
Bảng 1. Cấp phối bê tông (kg/m3)
Cát Đá Nước Phụ da N/X
829 1007 167 5,12 0,375
Điều kiện môi trường khi đổ xem như ít thay 
đổi và nhiệt độ của không khí được lấy bằng nhiệt 
độ trung bình t
tb
 (oC) của không khí. Để cho đơn 
giản xét hệ số trao đổi nhiệt đối lưu h (W/m2K) của 
không khí cũng không đổi ở tất cả các mặt tiếp xúc. 
Mặt đáy tiếp xúc với nền đất có nhiệt độ không đổi 
tn = ttb.
2.3. Mô hình toán học của đối tượng nghiên cứu
Quá trình truyền nhiệt trong khối bê tông 
dạng hình hộp ở đây có dạng phương trình vi phân 
sau viết cho một phân tố vô cùng nhỏ (coi hệ số dẫn 
nhiệt thay đổi theo mọi hướng là như nhau):
C
t
x
t
y
t
z
t
qv2
2
2
2
2
2
2
2
2
2
2
2
2
2t x m= + + +d n (8)
Điều kiện đơn trị:
x = 0, t = t
o
;x > 0, ;t h t2
2
xm D
- = (9)
Một cách tổng quát, đây là bài toán dẫn nhiệt 
không ổn định, có nguồn trong và các thông số nhiệt 
vật lý thay đổi hay còn gọi là bài toán dẫn nhiệt 
không ổn định phi tuyến [2]. Vì vậy, nếu sử dụng 
giải tích sẽ gặp nhiều khó khăn và ở đây chúng tôi 
sử dụng phương pháp gần đúng thường được dùng 
để giải quyết các bài toán truyền nhiệt phức tạp đó 
là phương pháp thể tích hữu hạn.
ISSN 2354-0575
Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 Journal of Science and Technology 19
2.4. Phương pháp thể tích hữu hạn tính toán 
trường nhiệt độ của khối bê tông
a. Cơ sở lý thuyết
Nội dung và cách sử dụng phương pháp này 
đã được trình bày kỹ trong [3,4], trong phạm vi bài 
báo này chúng tôi chỉ giới thiệu sơ lược về phương 
pháp thể tích hữu hạn như sau: Dựa trên nguyên tắc 
cân bằng nhiệt cho một phân tố thể tích V3 (Hình 
1) ta sẽ có “Tổng năng lượng phân tố nhận được tại 
nút thứ i bằng độ tăng nội năng của phân tố”.
 2 
1 
 4 
5 
6 
3 
i 
R1 
R2 
R3 
R4 
R5 
R6 
Hình 1. Cân bằng năng lượng cho phân tố i
.V F Cq R
t t t t
i
m
in
n
m
i
m
in i
i
m
i
m
n
1
1 1 1
1
6
xD D
+
-
=
-+
+ + +
=
/
 (10)
trong đó:
q
i
(m+1) (W/m3): năng suất sinh nhiệt thể tích 
của phân tố i ở thời điểm (m+1)
V3 (m3): thể tích của phân tố
F
in
 (m2): diện tích mặt thứ n của phân tố
R
t t
in
n
m
i
m
n
1 1
1
6 -+ +
=
/ (w): tổng năng lượng của các 
nút xung quanh phân tố ở thời điểm (m+1).
C
t t
i
i
m
i
m1
xD
-+ (w): độ tăng nội năng của phân 
tố sau khoảng thời gian 3x .
3x (s): bước thời gian tính.
R
in
 (K.m2/W): nhiệt trở thành phần của các 
nút xung quanh.
Nếu chia thể tích của khối bê tông thành n 
phân tố có thể tích V3 , viết phương trình cân bằng 
năng lượng cho n phân tố này dưới dạng (10) ta sẽ 
thu được n phương trình bậc nhất là n nhiệt độ trung 
bình của n phân tố V3 ở một thời điểm. Tính toán 
cho toàn bộ khoảng thời gian khảo sát ta sẽ thu được 
toàn bộ diễn biến thay đổi nhiệt độ của đối tượng 
theo thời gian.
b. Xác định phân bố nhiệt độ của khối bê 
tông đài móng
Do tính đối xứng, chúng tôi chỉ tính cho ¼ 
thể tích của khối bê tông có kích thước 2,3m#2,3m
#2,0m được đặt trên trục tọa độ như Hình 2.
x 
z 
0 
1 
2 
3 
4 
1 
2 
3 
4 
1 
2 
3 
4 
2,3m 
2m 
2,3m 
y 
∆y 
∆y/2 
∆z 
∆z/2 
∆x ∆x/2 
Hình 2. Sơ đồ chia phần tử của ¼ khối bê tông
Chia thể tích trên thành các phân tố có kích 
thước và thứ tự như sau: 
- Theo phương y: có 05 lớp được đánh số từ 
0 đến 4 bao gồm 03 lớp có Ty = 0,5m và 2 lớp tại 
đỉnh và đáyTy
đ
 =Ty/2 = 0,25m; 
- Theo phương x, z: có 05 lớp cũng được 
đánh số từ 0 đến 04 gồm 3 lớp cóTx =Tz = 0,575m 
và 2 lớp tại hai biên Txb =Tzb = Tx/2 =Tz/2 = 
0,2875m. 
Như vậy, ta sẽ có 05#05#05 = 125 phân 
tố của ¼ khối bê tông cần xác định nhiệt độ. Các 
phân tố này được ký hiệuT
x.y.z
 và chia kích thước 
như sau: 
- Phân tố tại đỉnh và đáy (08 phân tố):
TV
0.4.0
 =TV
4.4.0
 = TV
4.0.0
 = TV
0.0.0
 = TV
0.0.4
 = 
TV
0.4.4
 = TV
4.4.4
 =TV
4.0.4
 = 0,25#0,2875#0,2875 
= 0,0207 m3.
- Phân tố tại các lớp cạnh biên (36 phân tố) 
gồm: 24 phân tố có thể tích = 0,575#0,25#0,2875 
= 0,0413 m3 (i = 1÷3): TV
0.4.i
 = TV
0.0.i
 = TV
i.0.0
= TV
i.4.4
 = TV
i.4.0
 = TV
i.0.4
 = TV
4.0.i
 = TV
4.4.i
 ; 12 
phân tố có thể tích = 0,5#0,2585#0,2875 = 0,0335 
m3 (i = 1÷3): TV
0.i.0
 = TV
0.i.4
 = TV
4.i.0
 = TV
4.i.4
- Phân tố nằm trong của các lớp biên (54 
phân tố) gồm các phân tố có thể tích = 0,575#0,5
#0,2875 = 0,0827 m3 (i = 1÷3, n = 1÷3): TV
0.i.n
 = 
TV
4.i.n
 = TV
i.n.0
 = TV
i.n.4
 = TV
i.0.n
 = TV
i.4.n
.
- Phân tố nằm giữa (27 phân tố) gồm các 
phân tố có TV = 0,575#0,5#0,575 = 0,1653 m3 
(i = 1÷3, n = 1÷3, s = 1÷3):TV
i.n.s
Vì tính chất đối xứng nên một cách gần 
đúng, coi nhiệt độ ứng với các phân tố bằng nhau 
như sau: t
1.0.0
 = t
0.0.1
; t
1.1.0
 = t
0.1.0
 nên chúng tôi chỉ 
xác định nhiệt độ theo hướng x và hướng y. Do đó, 
tại một tiết diện theo phương y sẽ có 15 phân tố ứng 
với 1 lớp và tổng cộng sẽ có 15#5 = 75 phân tố. Từ 
ISSN 2354-0575
Journal of Science and Technology20 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016
đây rút ra được 75 phương trình bậc nhất theo dạng 
(10) với 75 ẩn là nhiệt độ trung bình của một phân 
tố trong một bước thời gian 3x . Nhiệt độ trung 
bình của bê tông trong (4) tính như sau:
.
t
V
t V t V
c
m
b
m
b i
m
i
1
1 1
D
D D
=
+
+
+ +
/
//
 (11)
ở đây: t
b
m+1 là nhiệt độ của phân tố biênTV
b
 ở thời 
điểm m + 1;
t
i
m+1 là nhiệt độ của các phân tố TV
b
 còn lại.
Quá trình tính toán được thực hiện lần lượt 
như sau:
1. Vào các thông số N/X; t
o
; t
r
; Qt; β; hx ; cm ; 
3x ; t ; E; R.
2. Tính các giá trị: αu; α; te; Qu; m ; Cp; tc lần 
lượt theo theo (2), (3), (4), (5) ,(6), (7) và (11).
3. Thay các thông số trên vào hệ phương 
trình bậc nhất, giải ra được các giá trị nhiệt độ tại 
các phân tố i ở thời điểm m.
4. Lấy các giá trị vừa tìm được tại thời điểm 
m làm các thông số đầu vào tại thời điểm m+1. Tiếp 
tục tính toán lại từ bước 2 đến thời điểm muốn dừng 
khảo sát hoặc đến khi nhiệt độ t
c
 trong hai bước liền 
nhau nhỏ hơn một giá trị cho trước nào đó.
Tiến hành tính toán trường nhiệt độ của ¼ 
khối bê tông đài móng theo các bước trên với các 
số liệu đầu vào được lấy như sau [1,10]: t
c
 = t
o
 = t
tb
= 28.7oC; cm = 2,9 W/mK; t = 2400 kg/m3; Qt = 90 
kJ/kg; hx = 36,147 giờ; β = 0,387; tr = 21oC;3x = 
60 phút, cách chọn theo phương pháp chia đôi đã 
được trình bày trong [4]. 
3. Kết quả tính toán
Sau khi thay các thông số và điều kiện ban 
đầu của khối bê tông, giải theo phương pháp thể tích 
hữu hạn kết hợp với phần mềm excel 2010 chúng 
tôi thu được kết quả là nhiệt độ của 75 phân tố ứng 
với 100 giờ (sau thời gian đạt nhiệt độ lớn nhất), 
chúng được biểu diễn dưới dạng đồ thị như sau:
Hình 3. Thay đổi nhiệt độ tại lớp 2 theo phương y
- Thay đổi nhiệt độ tại lớp thứ 2 (t
x.2.0
) theo 
phương y bao gồm nhiệt độ của 5 phân tố là t
0.2.0 
 đến 
t
4.2.0
 Hình 3. Qua kết quả tính toán và đồ thị Hình 3 
cho thấy nhiệt độ lớn nhất tại các phân tố đạt được 
chủ yếu ở khoảng thời gian bắt đầu từ giờ 75 đến 
95. Phân tố tại tâm có t
0.2.0
 đạt max bằng 86,7oC ở 
giờ thứ 75, các phân tố tiếp theo có t
max
 lần lượt 
bằng 73,1oC; 63,5oC; 52,4oC và 43,7oC ở sau mỗi 
khoảng 5 giờ. Sau đó nhiệt độ tại các vị trí đều giảm 
dần. Chênh lệch nhiệt độ tại tất cả các vị trí trong 
lớp 3 khi so với thời điểm đạt max được chúng tôi 
trình bày trong Hình 4.
Hình 4. Chênh lệch nhiệt độ giữa các phân tố so với 
phân tố tâm t
0.3.0
Chênh lệch nhiệt độ lớn nhất đối với phân tố 
ngoài cùng là Tt04 = t0.2.0 – t4.2.0 = 43,8oC, các phân 
tố khác cũng có sự tăng dần Tt đến giá trị lớn nhất 
nhưng đều nhỏ hơn 43,8oC, điều này được thể hiện 
rõ trên Hình 4. Ngoài ra, từ Hình 4 cũng dễ dàng 
nhận thấy sự chênh lệch nhiệt độ theo phương x của 
lớp này cũng giảm dần từ ngoài vào trong.
- Thay đổi nhiệt độ tại toàn bộ lớp ở tâm có 
(t
x.y.0
) được trình bày trên Hình 5. Các đường biểu 
diễn nhiệt độ cho thấy biến thiên cùng quy luật là 
chỉ có một giá trị nhiệt độ lớn nhất nhưng thời gian 
để đạt được giá trị này phụ thuộc vào vị trí và điều 
kiện biên của các phân tố khảo sát. Sự tăng nhiệt 
độ lớn nhất trong lớp này chính là tại các vị trí t
x.2.0
.
Hình 5. Diễn biến nhiệt độ của lớp có
 vị trí z = 0 (t
x.y.0 
)
ISSN 2354-0575
Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 Journal of Science and Technology 21
Tại lớp có tọa độ z = 1 (t
x.y.1
), sự gia tăng 
nhiệt độ có mức độ chậm hơn Hình 6. Độ chênh 
nhiệt độ giữa phân tố trong cùng và ngoài cùng khi 
nhiệt độ tại tâm đạt lớn nhất t
0.2.1 max
 = 73,1oC bằng 
Tt
04
 = t
0.2.1
 – t
4.2.1
 = 73,1 – 54,8 = 18,3oC.
Hình 6. Diễn biến nhiệt độ của lớp có vị trí z =1(t
x.y.1
)
Kết quả tính toán cho các lớp còn lại cũng 
được chúng tôi biểu diễn lần lượt trên Hình 7, Hình 
8 và Hình 9.
Hình 7. Diễn biến nhiệt độ của lớp có vị trí z =2(t
x.y.2
)
Sự gia tăng nhiệt độ lớn nhất vẫn ghi nhận ở 
phân tố có t
x.2.2
 và đạt max = 63,2oC ở giờ 85 nhưng 
độ chênh với vị trí ngoài cùng đã giảm đi so với 
lớp z = 1, cụ thể Tt
04
 = t
0.2.2
 – t
4.2.2
 = 63,2 – 47,4 = 
15,8oC.
Hình 8. Diễn biến nhiệt độ của lớp có vị trí z=3(t
x.y.3
)
Hình 9. Diễn biến nhiệt độ của lớp có vị trí z=4(t
x.y.4
)
Từ Hình 8, Hình 9 cho thấy càng ra ngoài 
biên, các phân tố chịu ảnh hưởng của điều kiện biên 
càng lớn làm cho sự tăng nhiệt độ tại mỗi môi phân 
giảm đi cả về tốc độ lẫn giá trị. Nếu như ở lớp có 
z=3 (t
x.y.3
) có nhiệt độ lớn nhất là t
0.2.3
 = 52,3oC ở giờ 
85 thì nhiệt độ lớn nhất ở lớp có z = 4 (t
x.y.4
) t
max
 = 
t
0.2.4
 = 35,3oC đạt được sau 90 giờ.
Như vậy, toàn bộ diễn biến nhiệt độ của ¼ 
khối bê tông đài móng đã được chúng tôi biểu diễn 
sau 100 giờ tính toán. 
So với kết quả tính toán của tác giả [1] 
cho thấy sau 85 giờ tại tâm có nhiệt độ lớn nhất 
là 90,4oC và tại biên là 43oC, độ chênh nhiệt độ 
lúc này bằng 47,4oC. Trong khi theo tính toán của 
chúng tôi, nhiệt độ lớn nhất tại tâm là 86,7oC sau 75 
giờ và nhiệt độ tại biên 42,9oC, độ chênh nhiệt độ 
là 43,8oC. Như vậy, về nhiệt độ lớn nhất sai lệch là 
4,1% và độ chênh nhiệt độ sai lệch 7,6%. Đặc biệt 
là thời gian đạt max theo tính toán của chúng tôi 
sớm hơn so với [1] là 10 giờ bằng 11,8%. Mặt khác 
theo báo cáo số liệu thực nghiệm cũng trong [1] cho 
thấy thời gian đạt max về nhiệt độ tại tâm là 79 giờ, 
tính toán của [1] là 85 giờ và chúng tôi dự đoán là 
75 giờ (sai lệch 5,06%).
4. Kết luận
Phương pháp tính toán trường nhiệt độ của 
khối bê tông đài móng khi xét đến sự thay đổi các 
hệ số nhiệt dung riêng, hệ số dẫn nhiệt và nguồn 
sinh nhiệt phụ thuộc vào hệ số mức độ thủy hóa do 
chúng tôi trình bày đã cho thấy tính phù hợp với 
quá trình hóa cứng của bê tông. Điều này trước đây 
rất ít tác giả đề cập đến khi tính toán. Kết quả cho 
thấy sự hợp lý về mặt giá trị và nhất là thời điểm đạt 
lớn nhất của nhiệt độ tâm khối bê tông. Qua đó, nó 
cho phép dự đoán một cách chính xác hơn diễn biến 
nhiệt độ trong khối bê tông để từ đó có biện pháp 
giảm thiểu sự ảnh hưởng của nhiệt độ đến kết cấu 
bê tông trong thời kỳ đầu mới đổ.
ISSN 2354-0575
Journal of Science and Technology22 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016
Tài liệu tham khảo
[1]. Hồ Ngọc Khoa, Nghiên cứu sự biến dạng các lớp bên trong của cấu kiện bê tông, thi công theo 
phương pháp toàn khối, trong thời gian đầu đóng rắn, Đề tài NCKH cấp trường, Trường Đại học 
Xây dựng, 2011.
[2]. Đặng Quốc Phú, Trần Thế Sơn, Trần Văn Phú, Truyền nhiệt, NXB Giáo dục, 2004.
[3]. Trương Minh Thắng, Nghiên cứu quy luật truyền nhiệt truyền chất trong bê tông kết rắn, 
LVTHS, Trường Đại học Bách khoa Hà Nội, 2007.
[4]. Trương Minh Thắng, Nguyễn Thị Thùy Dung, Xác định trường nhiệt độ của dầm bê tông dạng 
hình hộp trong điều kiện khí hậu Việt Nam, Tạp chí Khoa học & Công nghệ, Trường Đại học SPKT 
Hưng Yên, số 5/tháng 3- 2015. 
[5]. Tiêu chuẩn xây dựng Việt Nam TCXDVN 305:2004 “Bê tông khối lớn – Quy phạm thi công và 
nghiệm thu”, 03/09/2007
[6]. G. Deshutter và L. Taerwe, Specific Heat and Thermal Diffusivity of Hardening Conctete, 
Magazine of Concrete Research, 1995, 47, No. 172, Sept., 203-208.
[7]. Freisleben Hansen an, P., and Pedersen, E.J., “Maturity Computer for Controlling Curing and 
Hardening of Concrete”, Nordisk Betong Vol. 1, No 19, pp 21-25, 1977.
[8]. Mills, R.H., Factors Influencing Cessation of Hydration in Water-cured Cement Pastes, Special 
Report No. 90, Proceedings of the Symposium on the Structure of Portland Cement Paste and 
Concrete, Highway Research Board, Washington, D C., 406-424, 1996.
[9]. Schindler, A.K, Concrete Hydration, Temperature Evelopment and Setting at Early Ages, PhD 
dissertation, University of Texas at Austin. 2002.
[10]. Zhi Ge, Predicting Temperature and Strength Development of the Field Concrete, PhD 
dissertation, Iowa State University Ames, Iowa, 2005.
PREDICTING THE EARLY AGE TEMPERATURE RESPONSE OF MASS CONCRETE
Abstract:
The paper introduces the results of predicting temperatures profiles of the mass concrete at early 
age with variation of specific heat capacity, heat conduction and heat of hydration That all depend on 
the degree of hydration.
Keywords: Massive concrete, hydration of cement, temperaturesprofile.