Về đặc trưng cấu trúc tinh thể và trạng thái nền của một số vật liệu trong tính toán lý thuyết
Trong khoa học vật liệu, việc tính toán hoặc đo đạc các đặc trưng cơ bản của cấu trúc một vật liệu
mới đóng vai trò cơ bản trong xâu chuỗi phát triển công nghệ nano. Lý thuyết phiếm hàm mật độ là một
công cụ đắc lực, hiệu quả ngày nay đã được áp dụng vô cùng rộng rãi trong các nghiên cứu cơ bản và công
nghệ hiện đại. Trong báo cáo này chúng tôi giới thiệu phương pháp xác định một số đặc trưng cơ bản của
vật liệu thông qua tính tổng năng lượng của một số tinh thể sử dụng lý thuyết phiếm hàm mật độ. Tổng năng
lượng được tính toán cho các biến thiên hằng số mạng khác nhau. Đối với hệ có hai tham số biến thiên,
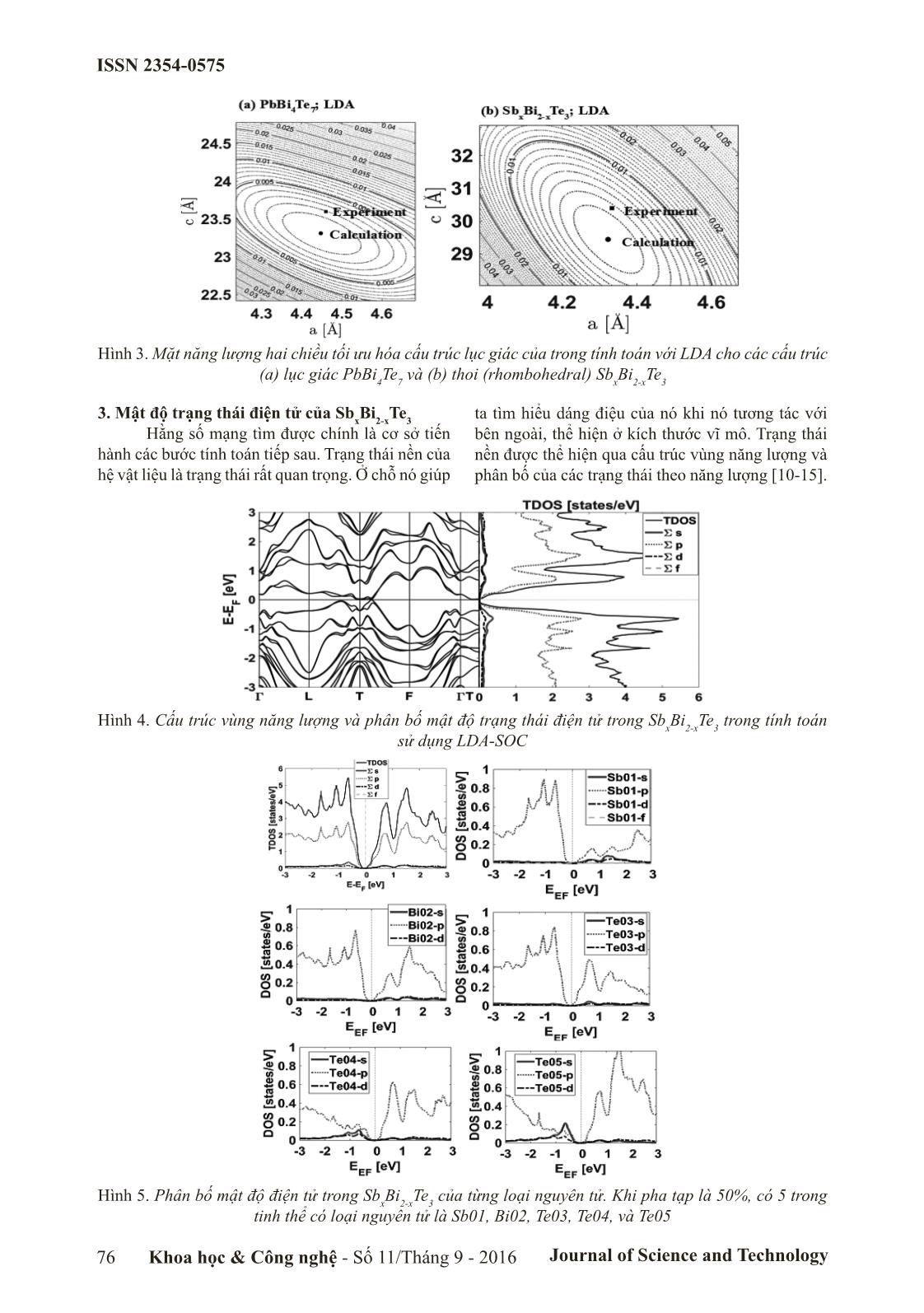
năng lượng thu được là một mặt hai chiều, rời rạc. Phương pháp nội suy cho ta mặt năng lượng trơn. Kết
quả thu được có thể sử dụng để tính toán cho các nghiên cứu về sau nhờ phân tích tác dụng của các nhân
tố bên ngoài lên cấu trúc mạng tinh thể. Khuynh hướng ảnh hưởng của các phương pháp xấp xỉ cũng được
thảo luận trong các tính toán. Chúng tôi cũng tính đến tương tác spin-quỹ đạo để mô tả các điện tử tương
đối tính và thực hiện tính toán cấu trúc điện tử của hợp chất trộn mới SbxBi2-xTe3 và tiến hành thảo luận tính
chất vận chuyển của nó và chỉ ra các khả năng của tác dụng việc thay thế nguyên tố.

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6
Tóm tắt nội dung tài liệu: Về đặc trưng cấu trúc tinh thể và trạng thái nền của một số vật liệu trong tính toán lý thuyết

g quát (generalized gradient approximation) hay GGA [5]. Cả hai cách xấp xỉ đều cho phép tính năng lượng trao đổi tương quan. Bên cạnh đó để mô tả các tính chất đặc trưng của hệ vật chất (như tính chất từ, quang phổ,) chính xác hơn, người ta còn đưa thêm các bổ chính gần đúng tinh tế hơn phù hợp với từng đối tượng, như tương tác spin quỹ đạo, Hubbard, vào Halmintonian. Để thực hiện giải (6), khi phiếm hàm năng lượng trao đổi đã biết, quỹ đạo ψ được phân tích vào không gian các hàm định nghĩa φ trực giao chuẩn hóa gọi là hệ cơ sở. Việc lựa chọn hệ cơ sở φ đưa đến những phương pháp tính toán khác nhau. Có hai phương pháp mà về nguyên tắc không cần đến các tham số thực nghiệm là phương pháp giả thế (pseudopotential method) và phương pháp điện tử toàn phần (all electron method) mà điển hình và nổi tiếng là phương pháp thế toàn phần sóng phẳng gia tăng. Phương pháp giả thế cho tốc độ tính toán nhanh và yêu cầu thiết bị tính toán đơn giản hơn so với phương pháp điện tử toàn phần. Ngược lại, phương pháp điện tử toàn phần cho phép tính toán chính xác, đặc biệt là những bài toán liên quan đến phân cực của lớp điện tử bên trong lớp hóa trị. Một lựa chọn tối ưu là tùy từng trường hợp và yêu cầu cụ thể của bài toán. 2. Tối ưu hóa cấu trúc tinh thể của một số hợp chất Trong hệ vật liệu, biểu thức tổng năng lượng (3) cho phép ta xác định trạng thái tồn tại của hệ. Bằng cách giải (6), sau đó thực hiện tính (3) ta sẽ thu được tổng năng lượng của hệ. Đây cũng là nguyên tắc cơ bản xác trạng thái tồn tại của hệ. Đối với bài toán ba chiều, việc thực hiện tính toán dựa trên đối xứng của tinh thể: đối xứng tịnh tiến cho phép thao tác công việc trên một ô mạng cơ sở, các đối xứng còn lại cho phép làm việc trong không gian không gian mạng đạo rút gọn Brillouin, vùng IBZ. Hình 1. Minh họa tối ưu hóa hằng số cấu trúc của các tinh thể lập phương khối (a) Si, (b) Ge, (c) Fe, (d) Pd ISSN 2354-0575 Khoa học & Công nghệ - Số 11/Tháng 9 - 2016 Journal of Science and Technology 75 Đối với những vật liệu tinh thể lập phương, bài toán xác định hằng số mạng chỉ đơn giản bằng cách thay đổi các hằng số mạng duy nhất, chẳng hạn tham số a, để tính tổng năng lượng theo các biến thiên này. Thời gian tính toán thông thường phụ thuộc vào kích thước của ô mạng. Tổng năng lượng thu được sẽ có dạng đường cong lõm. Điểm cực trị cho ta nhiều thông tin về cấu trúc mạng như hằng số mạng, mô dun khối,... Hình 1, chúng tôi thực hiện tính toán và biểu diễn tổng năng lượng của hệ tinh thể tính cho ô mạng cơ sở của các tinh thể lập phương Si, Ge, Fe và Pd. Lưu ý rằng hai vật liệu trước là bán dẫn phi từ, hai vật liệu sau là kim loại từ. Kết quả này thể hiện tính chính xác của lý thuyết phiếm hàm mật độ với sai khác cỡ vài %. Trong các tính toán này đã được thực hiện với gần đúng GGA. Trong sơ đồ xấp xỉ này các kết quả đều cho thấy có sự lệch về phía thể tích lớn hơn, nghĩa là hằng số mạng tính toán lớn hơn. Tuy nhiên với hệ lập phương, với điều kiện đối xứng tịnh tiến được giữ, ta chỉ cần biến thiên một biến số là hằng số đặc trưng a. Theo đó cả ba chiều đều thay đổi. Kết quả là ta có đường cong và dễ dàng dùng các phương pháp gần đúng khác nhau để tính hằng số mạng tinh thể. Đặc biệt là đối với việc tìm đồng thời cả mô đun khối ta phải dùng các phương trình trạng thái. Kết quả tính toán ở đây đã được sử dụng phương trình trạng thái Murhaghan [6]. ' ' / ' E V E V B B V B V V B V B 1 1 B 0 0 0 0 0 0 0 0 ' 0 = + - - - _ _ _i i i> H (6) Với E là năng lượng hệ, V là thể tích, B là modun khối. Chỉ số ‘0’ chỉ các đại lượng tương ứng ở trạng thái cân bằng (điểm cực trị năng lượng). Kết quả tìm được các hệ số cho ta biết hằng số mạng tương ứng đã chỉ ra trên Hình 1. Hình 2. Cấu trúc tinh thể PbBi4Te7 và hệ giả định thoi Sb x Bi 2-x Te3 Đối với hệ không phải lập phương, để tiến hành công việc ta phải biến thiên hằng số mạng theo các hướng khác nhau khả dĩ rồi tính tổng năng lượng đối với từng giá trị khả dĩ này. Với hệ lục giác (Hexagonal) hoặc hệ thoi (Rhombohedral), ta có hai hằng số cần biến thiên là a (in-plane) và c (cross- plane). Kết quả là ta thu được mặt năng lượng với các giá trị khác nhau của a và c. Trên Hình 2 chúng tôi trình bày kết quả tính toán với hai hệ lục giác PbBi 4 Te7 và hệ giả định thoi SbxBi2-xTe3. Đây là hai hợp chất đóng vai trò rất quan trọng trong khoa học và công nghệ nhiệt điện và topological insulator, lĩnh vực đang được thảo luận rất sôi nổi ngày nay do những tính chất kỳ lạ và đẹp đẽ của chúng, và với hứa hẹn mang lại nhiều lợi ích cho công nghệ tương lai [7-8]. Kết quả tính toán cho thấy mặt cong năng lượng có dạng lõm. Tuy nhiên để tìm được mặt này chính xác, độ chia phải nhỏ, nghĩa là khối lượng tính toán tăng lên. Để giảm khối lượng tính toán và đồng thời đạt được kết quả tương đối chính xác, chúng tôi đã sử dụng xấp xỉ spline hai chiều để làm trơn mặt năng lượng. Cực trị của mặt này nằm ở tâm (đánh dấu tròn đen) cho ta biết giá trị của hằng số mạng tính toán (Calculation) trên Hình 3. Để so sánh với thực nghiệm, điểm ô vuông được đánh dấu (Experiment) để so sánh. Các giá trị tìm được là rất phù hợp với kết quả thực nghiệm. Độ sai lệch đối với PbBi 4 Te7 là: δa = 1 - a a expr theor = 0.2% và δ c = 1 - a a expr theor = 1.2%. Giá trị lệch về phía nhỏ hơn thể hiện khuynh hướng thường thấy trong tác dụng của LDA trong bài toán tối ưu hằng số mạng. Đối với hợp chất giả định SbxBi2-xTe3, chúng tôi thiết lập hệ dựa vào sự thay thế của nguyên tử Sb trong tinh thể Bi 2 Te3. Kết quả này cho phép xác định hằng số mạng thực tế khi thực nghiệm tổng hợp được. Trên hình vẽ 3, điểm thực nghiệm (Experiment) được đo đạc đối với BiSbTe3 ở dạng dung dịch rắn (solid solution). Kết quả tính toán như sau: a BST = 4.32 Å, c BST = 29.45 Å các số liệu thực nghiệm tương ứng là a exp = 4.33 Å, c exp = 30.39 Å [9]. Ta có thể nhận thấy độ lệch so với công bố thực khá nhỏ: δ a = -0.2% và δ c = -3.1%. Giá trị nhỏ hơn trong tính toán thể hiện khuynh hướng của gần đúng LDA. ISSN 2354-0575 Journal of Science and Technology76 Khoa học & Công nghệ - Số 11/Tháng 9 - 2016 Hình 3. Mặt năng lượng hai chiều tối ưu hóa cấu trúc lục giác của trong tính toán với LDA cho các cấu trúc (a) lục giác PbBi4Te7 và (b) thoi (rhombohedral) SbxBi2-xTe3 3. Mật độ trạng thái điện tử của SbxBi2-xTe3 Hằng số mạng tìm được chính là cơ sở tiến hành các bước tính toán tiếp sau. Trạng thái nền của hệ vật liệu là trạng thái rất quan trọng. Ở chỗ nó giúp ta tìm hiểu dáng điệu của nó khi nó tương tác với bên ngoài, thể hiện ở kích thước vĩ mô. Trạng thái nền được thể hiện qua cấu trúc vùng năng lượng và phân bố của các trạng thái theo năng lượng [10-15]. Hình 4. Cấu trúc vùng năng lượng và phân bố mật độ trạng thái điện tử trong Sb x Bi 2-x Te3 trong tính toán sử dụng LDA-SOC Hình 5. Phân bố mật độ điện tử trong Sb x Bi 2-x Te3 của từng loại nguyên tử. Khi pha tạp là 50%, có 5 trong tinh thể có loại nguyên tử là Sb01, Bi02, Te03, Te04, và Te05 ISSN 2354-0575 Khoa học & Công nghệ - Số 11/Tháng 9 - 2016 Journal of Science and Technology 77 Trên hình vẽ 4, chúng tôi biểu diễn kết quả tính toán cấu trúc vùng năng lượng và mật độ trạng thái của SbxBi2-xTe3 trong gần đúng LDA-SOC. Ta biết rằng, đối với vật liệu tạo thành từ các nguyên tố nặng toán tử Halmitonian cần được bổ sung phần tương đối tính mô tả các điện tử gần hạt nhân, với số hạng mô tả tương tác spin quỹ đạo (Spin-orbital coupling, SOC). Hiệu ứng này do đó được đưa vào trong tính toán thể hiện trên Hình 4. Khi tính toán bao gồm SOC, các cực trị của vùng năng lượng gần mực Fermi có sự thay đổi đáng kể. Các cực trị chính dời khỏi các vị trí đối xứng cao làm cho độ suy biến tăng lên đáng kể (do tính đối xứng của tinh thể). Điều này có ý nghĩa to lớn, bởi vì nếu ta tìm được sự thay thế thích hợp, ta có thể tối ưu hóa độ suy biến đến cực đại. Sự việc này sẽ làm tăng đáng kể tính dẫn điện của bán dẫn này mà không làm giảm suất điện động nhiệt điện, khi xét khía cạnh tính chất nhiệt điện của hợp chất này. Việc tính toán cụ thể các hệ số này và tìm ra nhân tố quyết định trong việc thay thế này là một hướng phát triển tương lai của báo cáo này. Lưu ý rằng độ dốc của DOS gần mức Fermi thể hiện tính chất vận chuyển của hệ tinh thể: Độ dốc càng lớn thì suất điện động nhiệt điện càng lớn và hệ số phẩm chất điện tính (power factor) càng cao. Tính chất này dẫn tới khả năng doping tạo bán dẫn loại p-type sẽ tốt hơn [16-17]. Khi đó đóng góp cho các tính chất vận chuyển chủ yếu đến từ trạng thái p của các nguyên tố Sb, Bi và của cả Te. Nhưng khi ta thực hiện n-doping, thì ta sẽ thu được sự đóng góp chủ yếu của các Te còn lại, nhưng độ dốc của DOS trong trường hợp lại giảm đi chút ít. Cần phải nói thêm rằng, khi chúng ta tính đến SOC, tuy dáng điệu của các band (band topology) ở gần mức Fermi cho kết quả hợp lý, nhưng cấu trúc vùng lại bị kéo xích lại gần nhau giữa vùng dẫn và vùng hóa trị. Kết quả là ta có sự thu nhỏ của vùng cấm khá nhiều. Vấn đề này có thể được giải quyết bằng cách đưa vào tương tác che chắn (screened exchange) [18-19]. Chúng tôi sẽ cập nhật tính toán phức tạp này và đồng thời sẽ tiến hành các đo đạc thực nghiệm trong tương lai để so sánh. Kết quả sẽ được công bố trong một công trình khác, 4. Kết luận Trong báo cáo này chúng tôi đã giới thiệu sơ bộ về lý thuyết phiếm hàm mật độ, và áp dụng tính toán thu lại các kết quả cho các cấu trúc lập phương để minh họa sự phù hợp. Chúng tôi tiến hành nghiên cứu hai hệ lục giác điển hình mới là PbBi 4 Te7 và SbxBi2-xTe3.Chúng tôi áp dụng lý thuyết tính tổng năng lượng cho hai hợp chất quan trọng này bằng cách biến thiên hằng số mạng theo hai hướng in- plane và cross-plane. Kết quả mặt năng lượng hai chiều cho phép xác định các thông số mạng. Để nghiên cứu cấu trúc vùng điện tử của hợp chất giả định SbxBi2-xTe3, chúng tôi đã sử dụng tương tác spin quỹ đạo để mô tả và thu được bằng chứng về những lợi ích của SbxBi2-xTe3 khi được thực hiện p-doping trong tính chất nhiệt điện. Kết quả báo cáo gợi mở cho những nghiên cứu thực nghiệm về hợp chất này, và tính toán mở rộng phát triển trong nghiên cứu vật liệu thực tế khi áp dụng những phương pháp tính toán chính xác hơn, và xa hơn. Lời cảm ơn Nghiên cứu này được tài trợ bởi Quỹ Phát triển khoa học và công nghệ Quốc gia (NAFOSTED) trong đề tài mã số 103.01-2015.11. Tài liệu tham khảo [1]. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev. B 136, 864 (1964). [2]. W. Koch, M. C. Holthausen, A Chemist’s Guide to Density Functional Theory, 001 Wiley-VCH Verlag GmbH, ISBNs: 3-527-30372-3, 30 (2001). [3]. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev. 140, A1133 (1965). [4]. L. Hedin, B. I. Lundqvist, Explicit Local Exchange-correlation Potentials, J. Phys. C: Solid State Phys. 4, 2064 (1971); U. von Barth, L. Hedin, J. Phys. C 5, 1629 (1972). [5]. J. P. Perdew, K. Burke, M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77, 3865 (1996); Phys. Rev. Lett. 78, 1396 (1997). [6]. Murnaghan, F. D. The Compressibility of Media under Extreme Pressures. Proc. N. A. S. 30, 244–247 (1944). [7]. G. J. Snyder and E. S. Toberer, Complex Thermoelectric Materials, Natural Materials 7, 105 (2008). [8]. R. Venkatasubramanian, E. Siivola, T. Colpitts, and B. O’Quinn, Thin-film Thermoelectric Devices with High Room-temperature Figures of Merit, Nature 413, 597 (2001). [9]. M. K. Jacobsen, R. S. Kumar, A. L. Cornelius, S. V. Sinogeiken, and M. F. Nicol, AIP Conf. Proc. 955, 171 (2007). ISSN 2354-0575 Journal of Science and Technology78 Khoa học & Công nghệ - Số 11/Tháng 9 - 2016 [10]. E. Wimmer, H. Krakauer, M. Weinert, and A. J. Freeman, Full-potential Self-consistent Linearized-augmented-plane-wave Method for Calculating the Electronic Structure of Molecules and Surfaces: O2 Molecule, Phys. Rev. B 24, 864 (1981). [11]. P. Giannozzi et al. QUANTUM ESPRESSO: A Modular and Open-source Software Project for Quantum Simulations of Materials. J. Phys. Condens. matter 395502, (2009). [12]. S. J. Youn and A. J. Freeman, First-principles Electronic Structure and its Relation to Thermoelectric Properties of Bi2Te3, Phys. Rev. B 63, 085112 (2001). [13]. Tran Van Quang, Miyoung Kim, The Thermoelectric Transport Properties of Bi2Te3 under the Substitutions of Rare Earths, KPS meeting, DG-40*, p37, Peongchang, 24-26/10/2012 [14]. M. Kim, A. J. Freeman, and C. B. Geller, Screened Exchange LDA Determination of the Ground and Excited State Properties of Thermoelectrics: Bi2Te3, Phys. Rev. B 72, 035205, (2005); S. J. Youn and A. J. Freeman, Phys. Rev. B 63, 085112 (2001). [15]. Tran Van Quang, Hanjo Lim, and Miyoung Kim, Temperature and Carrier-concentration Dependences of the Thermoelectric Properties of Bismuth Selenide Dioxide Compounds, JKPS 61, 1728 (2012); ISSN: 0374-4884 (print version); ISSN: 1976-8524 (electronic version) [16]. G. D. Mahan and J. O. Sofo, The Best Thermoelectric, Proc. Natl. Acad. Sci. U.S.A. 93, 7436 (1996). [17]. Tran Van Quang, Miyoung Kim, Spin Orbit Coupling and Correlation Effect on the Structural Optimization of Telluride Alloys; First-principles Approach, KOMAG, 2012. [18]. M. S. Park, J. H. Song, J. E. Medvedeva, M. Kim, I. G. Kim, and A. J. Freeman, Phys. Rev. B 81, 155211 (2010). [19]. M. Kim, A. J. Freeman, and C. B. Geller, Phys. Rev. B 72, 035205 (2005). DETERMINATION OF STRUCTURAL AND GROUND STATE PROPERTIES OF SOME MATERIALS USING DENSITY FUNCTIONAL THEORY Abstract: Structural optimization is potentially important to determine the chareristic of a new material, especially in nano-material science. Density functional theory, which have been applied extensively in recent years, emerges as an efficient method to study real materials applied in many desciplines of nano science and technology. In this report, we introduce biefly the theory and its application in the structural optimization by estimating the total energy of some materials. For the cubic structure materials, with a fit model, we find a curve to figure out the optimal point. For the system with two variations of lattice parameters, we compute total energies for obtaining a surface. Smooth surface is obtained by 2D spline fitting method. A discussion of the effect of approximations used in each case is given. The electronic structure calculation of Sb x Bi 2-x Te3 is performed to clarify some aspects of its transport property and the effect of elecment substitution Sb-Bi, in which the spin-orbital coupling for relativistic-effect description has been included. Keywords:
File đính kèm:
 ve_dac_trung_cau_truc_tinh_the_va_trang_thai_nen_cua_mot_so.pdf
ve_dac_trung_cau_truc_tinh_the_va_trang_thai_nen_cua_mot_so.pdf

