Tính toán và mô phỏng số hiệu quả giảm dao động xoắn cho trục máy khi sử dụng bộ hấp thụ động lực DVA

iên cứu này, mô hình trục gồm một lò xo có độ 
cứng xoắn là k
s
 (Nm), và một đĩa có mô men quán 
tính khối lượng là Jr , trục máy quay đều với vận tốc 
góc Ω
0
 (s-1) và chịu cản môi trường có hệ số cản là 
c
s
 (kgm2s-2).
Hình 1. Mô hình trục máy có lắp bộ hấp thụ dao 
động DVA
ISSN 2354-0575
Journal of Science and Technology28 Khoa học & Công nghệ - Số 15/Tháng 9 - 2017
Bộ hấp thụ dao động DVA bao gồm một 
rotor (lắp với phần ngõng trục thông qua moay ơ) 
và một đĩa bị động. Rotor và đĩa bị động được liên 
kết với nhau thông qua n bộ lò xo - giảm chấn. Bán 
kính quán tính và mô men quán tính khối lượng của 
rotor và đĩa bị động lần lượt là ρr , Jr , ρa , Ja. 
Độ cứng của mỗi lò xo là k
a
 (N/m), hệ số 
cản nhớt của mỗi giảm chấn là c
a
 (Ns/m). Góc quay 
của rotor là φr (rad), góc quay tương đối giữa đĩa bị 
động và rotor là φ
a
 (rad). Góc xoắn θ(t) giữa hai đầu 
ngõng trục được xác định θ(t) = φ
r
(t)-Ω
0
(t), rad. Hệ 
phương trình vi phân mô tả dao động xoắn của hệ 
được biểu diễn như sau:
Mq Cq Kq F+ + =p o (1) 
trong đó véc tơ tọa độ suy rộng, ma trận khối lượng, 
ma trận cản, ma trận độ cứng, véc tơ lực kích động 
lần lượt được biểu diễn như sau:
q a Ti {= " , M 1 22
2
2
nh
nh
nh
nh
=
+= G
n
C
0
0
0
s
2pa nmX
= = G
K
n0
0s
s
2
2 2 2a nc
X
X
= > H ( )mM tF 0r r
T
2t
= * 4
Hình 2. Mô hình bộ hấp thụ dao động DVA
Mục đích của các nghiên cứu [3], [4], [5], [7] 
là với những thông số thiết kế đầu vào đã xác định, 
bao gồm các thông số μ, η, γ và λ, yêu cầu xác định 
hai thông số tối ưu α và tỉ số cản nhớt ξ dưới dạng 
giải tích phụ thuộc vào các thông số đã biết, nhằm 
mục đích giảm dao động xoắn cho trục đạt hiệu quả 
cao nhất. Thông số tối ưu α giúp người thiết kế, chế 
tạo có thể chọn được lò xo tối ưu, tỉ số cản nhớt ξ 
tối ưu cho phép chọn dầu giảm chấn phù hợp nhất. 
Các kết quả nghiên cứu trong [3], [4], [5], [7] được 
liệt kê trong Bảng 1.
Bảng 1. Các tham số tối ưu của bộ hấp thụ dao động theo các phương pháp khác nhau
Kích động (Phương pháp) αopt ξopt
Kích động điều hòa 
(Hai điểm cố định) n 12c nh
h
+_ i ( )n2 1
3
2
2
2m
ch
nh
n
+
Kích động ngẫu nhiên
(Cực tiểu mô men bậc hai) ( )
( )
n
n
2
2
1
2
2
2
c nh
h nh
+
+
( ) ( )
( )
n2 1 2
2 4 3
2
2
2 2
2
m
ch
nh nh
n nh
+ +
+
Kích động ngẫu nhiên
(Cực đại độ cản tương đương) ( )n 1 2c nh
h
+ n2
2
m
ch n
Kích động va chạm
(Cực tiểu hóa năng lượng) ( )
( )
n
n
2 1
2 2
2
2
c nh
h nh
+
-
( ) ( )
( )
n1 2 2
4 3
2 2 2
2 2 2 4
nh m nh
ch n nh n h
+ -
+ -
2. Tính toán, mô phỏng số hiệu quả giảm dao 
động xoắn cho trục máy
Để thuận tiện trong mô phỏng số và tính toán 
hiệu quả giảm dao động theo các phương pháp giải 
tích, tác giả ký hiệu DVA-FPM, DVA-MQT, DVA-
MEVR và DVA-MKE lần lượt là thiết kế DVA với 
các nghiệm tối ưu được xác định theo phương pháp 
hai điểm cố định, phương pháp cực tiểu mô men 
bậc hai, phương pháp cực đại độ cản tương đương 
và phương pháp cực tiểu hóa năng lượng (Bảng 1). 
Gọi E là phần năng lượng truyền từ trục (hệ chính) 
sang bộ hấp thụ động lực DVA [1], [6], năng lượng 
E được xác định như sau:
( ) ( )E t tai {= o p (2) 
Để có thể phân tích và đánh giá hiệu quả 
giảm dao động của các thiết kế DVA theo từng 
phương pháp, tiêu chuẩn tính toán và các kích động 
khác nhau, tác giả sử dụng công thức trong [1], [6]:
]
] ]
. %H
i
i i
100
[
[ [
k
k l
2
2 2
i
i i
=
-
3
33
t
t t
/
//
 (3) 
trong đó:
H là hiệu quả giảm dao động khi kết cấu có 
lắp DVA, %; kit là đường bao đáp ứng của kết cấu 
khi chưa lắp DVA, rad; lit là đường bao đáp ứng 
của kết cấu khi lắp DVA, rad.
ISSN 2354-0575
Khoa học & Công nghệ - Số 15/Tháng 9 - 2017 Journal of Science and Technology 29
• Số liệu mô phỏng:
Trục có độ cứng xoắn k
s
 = k1 = 1.125.10
5 
kgm2/s2 và chịu cản môi trường có hệ số cản nhớt 
c
s 
= c1 = 22.5 kgm
2/s. Mô men quán tính khối lượng 
của trục Jr = I1 = 1.125.10
-1 kgm2. Trục có bán kính 
quán tính ρr = 0.15 m. [2]
Các số liệu thiết kế đã biết (được chọn trước 
và yêu cầu kỹ thuật của quy trình thiết kế và lắp 
ráp) của bộ hấp thụ DVA bao gồm: Số lò xo-cản 
nhớt sử dụng: n = 4; Bán kính quán tính của đĩa 
DVA: ρ
a
 = 0.15m; Khoảng cách lắp ráp lò xo: e1 = 
0.075m; Khoảng cách lắp bộ cản nhớt: e2 = 0.12m; 
Khối lượng đĩa DVA: m
a
 = 0.2 kg; Mô men quán 
tính khối lượng của đĩa DVA: J
a
 = 4.5.10-3 kgm2
Với bộ số liệu trên, các đại lượng không thứ 
nguyên được xác định như sau: μ = 4%; η = 1; γ=0.5 
và λ = 0.8. Các giá trị tối ưu của tỷ số α và tỷ số cản 
nhớt ξ xác định theo các phương pháp trên được mô 
tả trong Bảng 2.
Bảng 2. Dữ liệu số của các tham số tối ưu
Thiết kế tối ưu αopt ξopt
DVA-FPM 0.961 0.093
DVA-MQT 0.971 0.076
DVA-MEVR 0.980 0.078
DVA-MKE 0.951 0.076
• Mô phỏng số đáp ứng dao động xoắn 
của trục khi chịu kích động điều hòa
Khi trục máy chịu kích động điều hòa thì 
thiết kế tối ưu phù hợp là DVA-FPM. [3], [5]. Mô 
men kích động điều hòa có dạng: M = M
0
sin(ωt) 
với biên độ của kích động M
0
 = 200 Nm. Để thấy 
được hiệu quả giảm dao động xoắn, mô phỏng được 
thực hiện trong trường hợp hệ chính không cản và 
có cản (c
s
 = 22.5 kgm2/s [2]). Với các số liệu mô 
phỏng trên, hệ sẽ xảy ra cộng hưởng tại các tần số ω 
của kích động lần lượt là 887.41, 980.58 và 1083.52 
s-1. Trong các tính toán và mô phỏng sau đây tác giả 
thực hiện với tần số của kích động là ω = 1000 s-1 
(hệ làm việc trong vùng cộng hưởng). Các đáp ứng 
của hệ chính khi lắp bộ hấp thụ dao động DVA-
FPM khi hệ làm việc trong vùng cộng hưởng được 
thể hiện trên các Hình 3 và Hình 4.
Hình 3 mô tả hiệu quả giảm dao động xoắn 
của trục máy khi lắp bộ hấp thụ dao động DVA-
FPM. Khi hệ chịu kích động tuần hoàn với tần số 
của kích động là ω = 1000s-1 (vùng tần số cộng 
hưởng), kết quả tính toán hiệu quả giảm dao động 
xoắn theo công thức (3) được liệt kê trong Bảng 3.
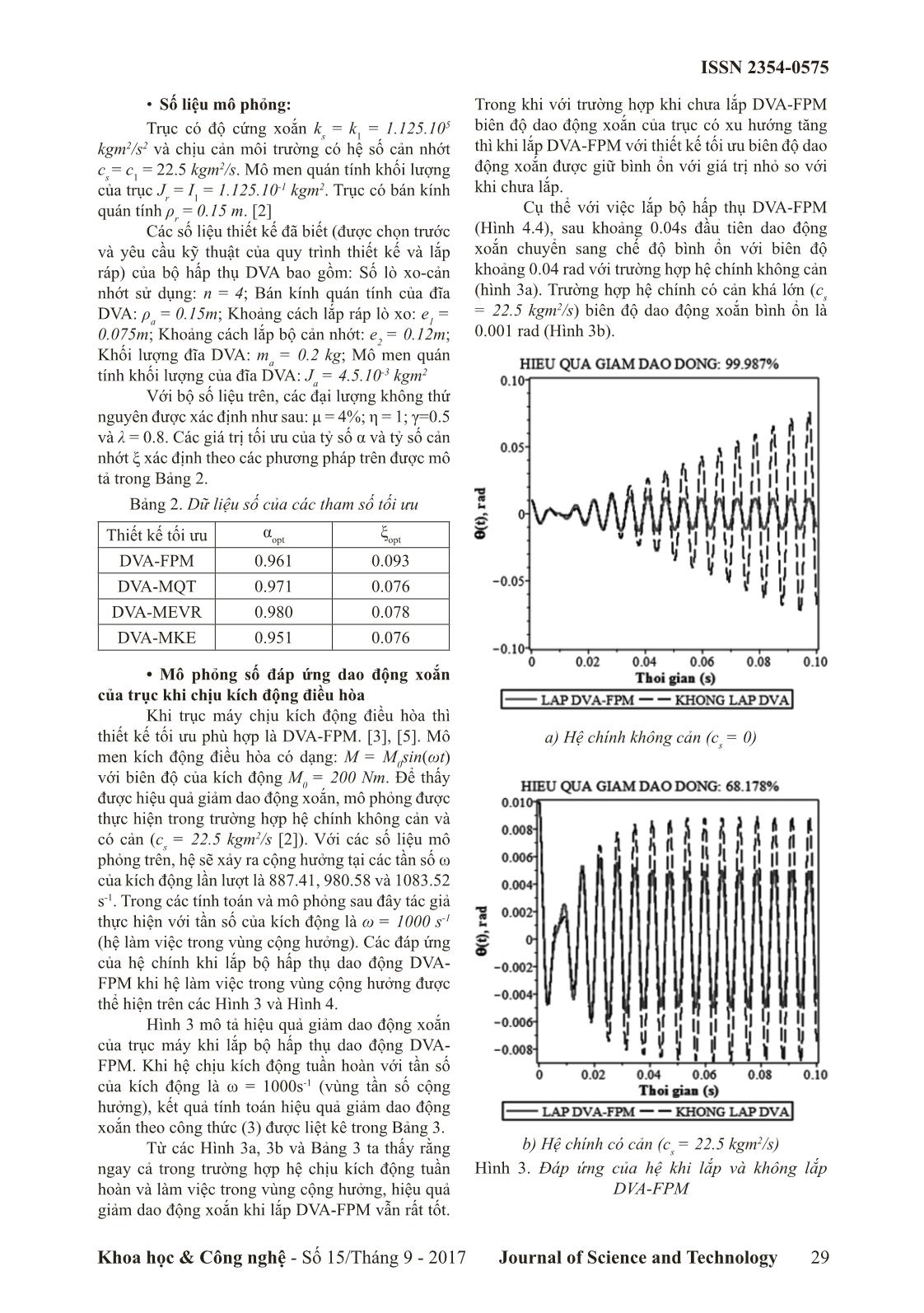
Từ các Hình 3a, 3b và Bảng 3 ta thấy rằng 
ngay cả trong trường hợp hệ chịu kích động tuần 
hoàn và làm việc trong vùng cộng hưởng, hiệu quả 
giảm dao động xoắn khi lắp DVA-FPM vẫn rất tốt. 
Trong khi với trường hợp khi chưa lắp DVA-FPM 
biên độ dao động xoắn của trục có xu hướng tăng 
thì khi lắp DVA-FPM với thiết kế tối ưu biên độ dao 
động xoắn được giữ bình ổn với giá trị nhỏ so với 
khi chưa lắp. 
Cụ thể với việc lắp bộ hấp thụ DVA-FPM 
(Hình 4.4), sau khoảng 0.04s đầu tiên dao động 
xoắn chuyển sang chế độ bình ổn với biên độ 
khoảng 0.04 rad với trường hợp hệ chính không cản 
(hình 3a). Trường hợp hệ chính có cản khá lớn (c
s
= 22.5 kgm2/s) biên độ dao động xoắn bình ổn là 
0.001 rad (Hình 3b).
a) Hệ chính không cản (c
s
 = 0)
b) Hệ chính có cản (c
s
 = 22.5 kgm2/s)
Hình 3. Đáp ứng của hệ khi lắp và không lắp 
DVA-FPM
ISSN 2354-0575
Journal of Science and Technology30 Khoa học & Công nghệ - Số 15/Tháng 9 - 2017
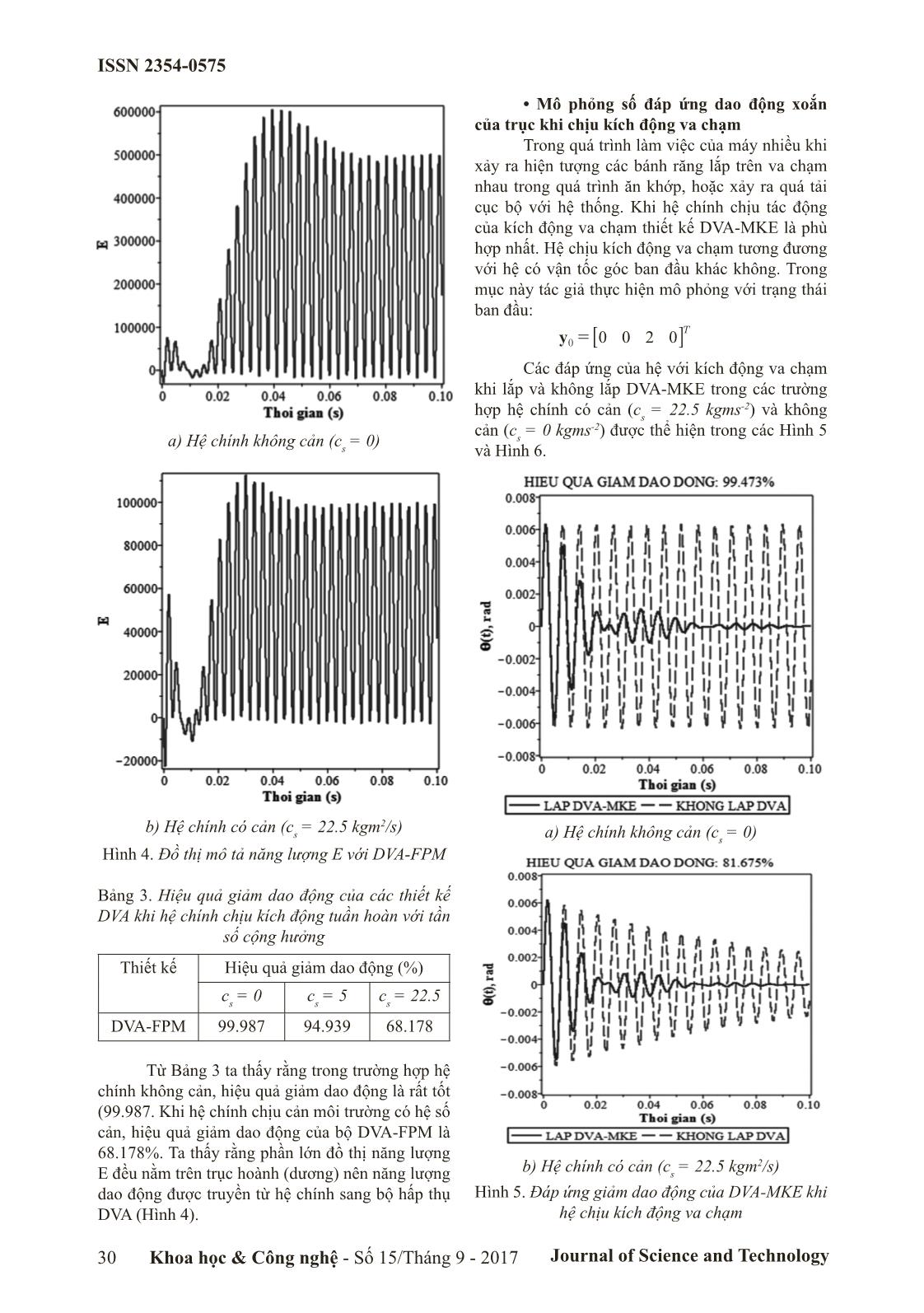
a) Hệ chính không cản (c
s
 = 0)
b) Hệ chính có cản (c
s
 = 22.5 kgm2/s)
Hình 4. Đồ thị mô tả năng lượng E với DVA-FPM
Bảng 3. Hiệu quả giảm dao động của các thiết kế 
DVA khi hệ chính chịu kích động tuần hoàn với tần 
số cộng hưởng
Thiết kế Hiệu quả giảm dao động (%)
c
s
 = 0 c
s
 = 5 c
s
 = 22.5
DVA-FPM 99.987 94.939 68.178
Từ Bảng 3 ta thấy rằng trong trường hợp hệ 
chính không cản, hiệu quả giảm dao động là rất tốt 
(99.987. Khi hệ chính chịu cản môi trường có hệ số 
cản, hiệu quả giảm dao động của bộ DVA-FPM là 
68.178%. Ta thấy rằng phần lớn đồ thị năng lượng 
E đều nằm trên trục hoành (dương) nên năng lượng 
dao động được truyền từ hệ chính sang bộ hấp thụ 
DVA (Hình 4).
• Mô phỏng số đáp ứng dao động xoắn 
của trục khi chịu kích động va chạm
Trong quá trình làm việc của máy nhiều khi 
xảy ra hiện tượng các bánh răng lắp trên va chạm 
nhau trong quá trình ăn khớp, hoặc xảy ra quá tải 
cục bộ với hệ thống. Khi hệ chính chịu tác động 
của kích động va chạm thiết kế DVA-MKE là phù 
hợp nhất. Hệ chịu kích động va chạm tương đương 
với hệ có vận tốc góc ban đầu khác không. Trong 
mục này tác giả thực hiện mô phỏng với trạng thái 
ban đầu:
Các đáp ứng của hệ với kích động va chạm 
khi lắp và không lắp DVA-MKE trong các trường 
hợp hệ chính có cản (c
s
 = 22.5 kgms-2) và không 
cản (c
s
 = 0 kgms-2) được thể hiện trong các Hình 5 
và Hình 6.
a) Hệ chính không cản (c
s
 = 0)
b) Hệ chính có cản (c
s
 = 22.5 kgm2/s)
Hình 5. Đáp ứng giảm dao động của DVA-MKE khi 
hệ chịu kích động va chạm
y 0 0 2 0 T0 = 7 A
ISSN 2354-0575
Khoa học & Công nghệ - Số 15/Tháng 9 - 2017 Journal of Science and Technology 31
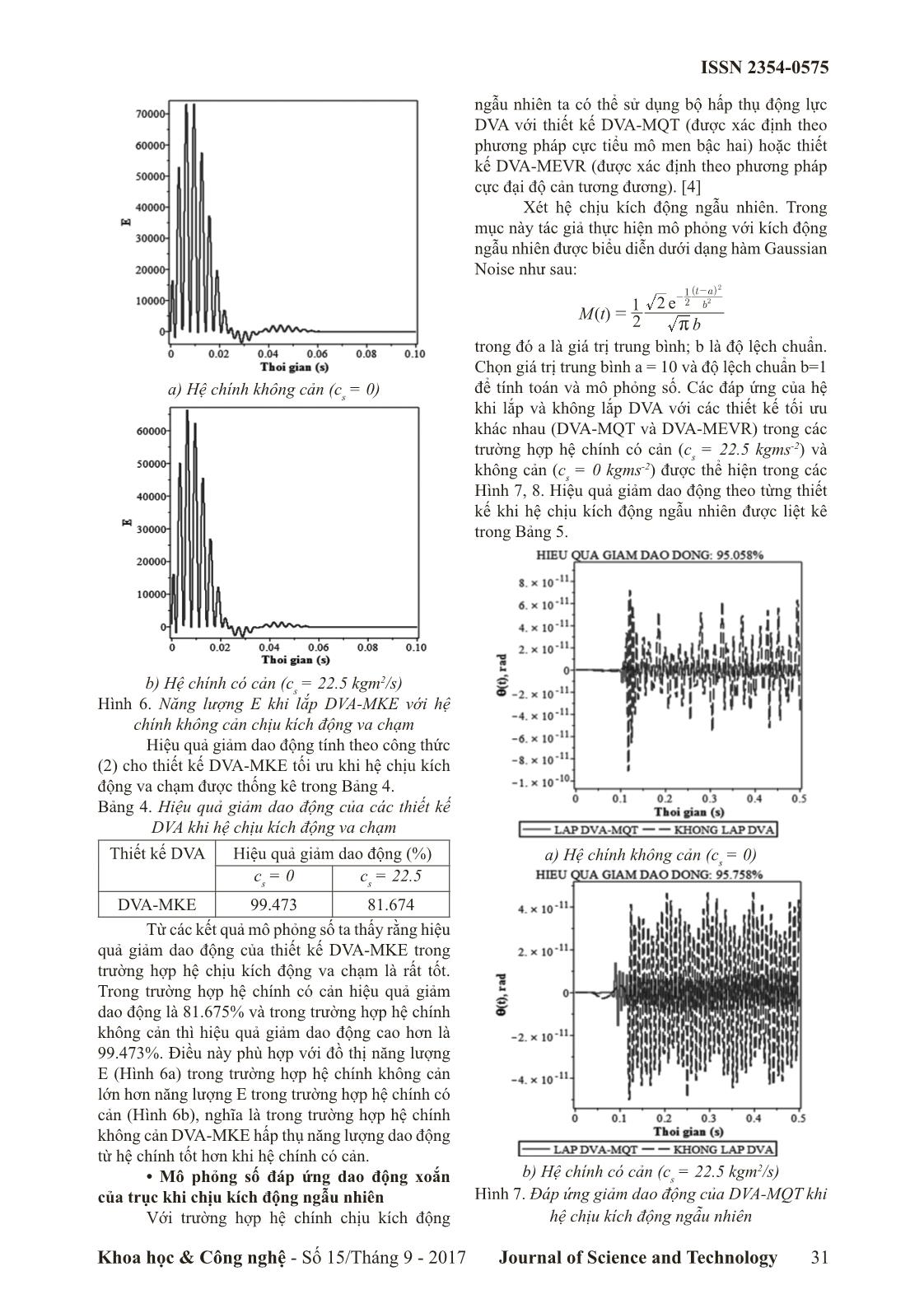
a) Hệ chính không cản (c
s
 = 0)
b) Hệ chính có cản (c
s
 = 22.5 kgm2/s)
Hình 6. Năng lượng E khi lắp DVA-MKE với hệ 
chính không cản chịu kích động va chạm
Hiệu quả giảm dao động tính theo công thức 
(2) cho thiết kế DVA-MKE tối ưu khi hệ chịu kích 
động va chạm được thống kê trong Bảng 4.
Bảng 4. Hiệu quả giảm dao động của các thiết kế 
DVA khi hệ chịu kích động va chạm
Thiết kế DVA Hiệu quả giảm dao động (%)
c
s
 = 0 c
s
 = 22.5
DVA-MKE 99.473 81.674
Từ các kết quả mô phỏng số ta thấy rằng hiệu 
quả giảm dao động của thiết kế DVA-MKE trong 
trường hợp hệ chịu kích động va chạm là rất tốt. 
Trong trường hợp hệ chính có cản hiệu quả giảm 
dao động là 81.675% và trong trường hợp hệ chính 
không cản thì hiệu quả giảm dao động cao hơn là 
99.473%. Điều này phù hợp với đồ thị năng lượng 
E (Hình 6a) trong trường hợp hệ chính không cản 
lớn hơn năng lượng E trong trường hợp hệ chính có 
cản (Hình 6b), nghĩa là trong trường hợp hệ chính 
không cản DVA-MKE hấp thụ năng lượng dao động 
từ hệ chính tốt hơn khi hệ chính có cản.
• Mô phỏng số đáp ứng dao động xoắn 
của trục khi chịu kích động ngẫu nhiên
Với trường hợp hệ chính chịu kích động 
ngẫu nhiên ta có thể sử dụng bộ hấp thụ động lực 
DVA với thiết kế DVA-MQT (được xác định theo 
phương pháp cực tiểu mô men bậc hai) hoặc thiết 
kế DVA-MEVR (được xác định theo phương pháp 
cực đại độ cản tương đương). [4] 
Xét hệ chịu kích động ngẫu nhiên. Trong 
mục này tác giả thực hiện mô phỏng với kích động 
ngẫu nhiên được biểu diễn dưới dạng hàm Gaussian 
Noise như sau:
( )M t b2
1 2 e
( )
b
t a
2
1
2
2
r
=
-
-
trong đó a là giá trị trung bình; b là độ lệch chuẩn. 
Chọn giá trị trung bình a = 10 và độ lệch chuẩn b=1 
để tính toán và mô phỏng số. Các đáp ứng của hệ 
khi lắp và không lắp DVA với các thiết kế tối ưu 
khác nhau (DVA-MQT và DVA-MEVR) trong các 
trường hợp hệ chính có cản (c
s
 = 22.5 kgms-2) và 
không cản (c
s
 = 0 kgms-2) được thể hiện trong các 
Hình 7, 8. Hiệu quả giảm dao động theo từng thiết 
kế khi hệ chịu kích động ngẫu nhiên được liệt kê 
trong Bảng 5.
a) Hệ chính không cản (c
s
 = 0)
b) Hệ chính có cản (c
s
 = 22.5 kgm2/s)
Hình 7. Đáp ứng giảm dao động của DVA-MQT khi 
hệ chịu kích động ngẫu nhiên
ISSN 2354-0575
Journal of Science and Technology32 Khoa học & Công nghệ - Số 15/Tháng 9 - 2017
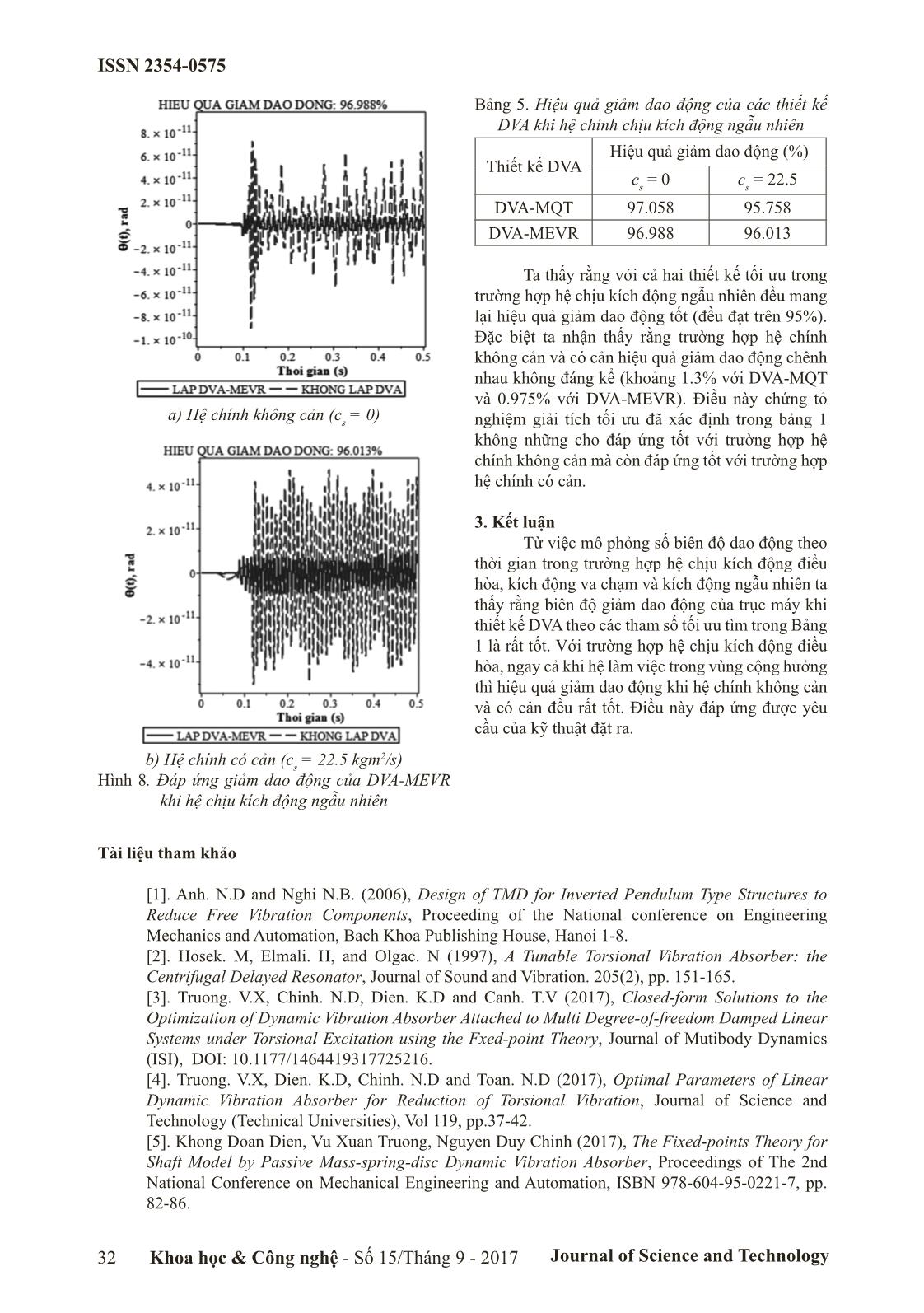
a) Hệ chính không cản (c
s
 = 0)
b) Hệ chính có cản (c
s
 = 22.5 kgm2/s)
Hình 8. Đáp ứng giảm dao động của DVA-MEVR 
khi hệ chịu kích động ngẫu nhiên
Bảng 5. Hiệu quả giảm dao động của các thiết kế 
DVA khi hệ chính chịu kích động ngẫu nhiên
Thiết kế DVA
Hiệu quả giảm dao động (%)
c
s
 = 0 c
s
 = 22.5
DVA-MQT 97.058 95.758
DVA-MEVR 96.988 96.013
Ta thấy rằng với cả hai thiết kế tối ưu trong 
trường hợp hệ chịu kích động ngẫu nhiên đều mang 
lại hiệu quả giảm dao động tốt (đều đạt trên 95%). 
Đặc biệt ta nhận thấy rằng trường hợp hệ chính 
không cản và có cản hiệu quả giảm dao động chênh 
nhau không đáng kể (khoảng 1.3% với DVA-MQT 
và 0.975% với DVA-MEVR). Điều này chứng tỏ 
nghiệm giải tích tối ưu đã xác định trong bảng 1 
không những cho đáp ứng tốt với trường hợp hệ 
chính không cản mà còn đáp ứng tốt với trường hợp 
hệ chính có cản.
3. Kết luận
Từ việc mô phỏng số biên độ dao động theo 
thời gian trong trường hợp hệ chịu kích động điều 
hòa, kích động va chạm và kích động ngẫu nhiên ta 
thấy rằng biên độ giảm dao động của trục máy khi 
thiết kế DVA theo các tham số tối ưu tìm trong Bảng 
1 là rất tốt. Với trường hợp hệ chịu kích động điều 
hòa, ngay cả khi hệ làm việc trong vùng cộng hưởng 
thì hiệu quả giảm dao động khi hệ chính không cản 
và có cản đều rất tốt. Điều này đáp ứng được yêu 
cầu của kỹ thuật đặt ra.
Tài liệu tham khảo
[1]. Anh. N.D and Nghi N.B. (2006), Design of TMD for Inverted Pendulum Type Structures to 
Reduce Free Vibration Components, Proceeding of the National conference on Engineering 
Mechanics and Automation, Bach Khoa Publishing House, Hanoi 1-8.
[2]. Hosek. M, Elmali. H, and Olgac. N (1997), A Tunable Torsional Vibration Absorber: the 
Centrifugal Delayed Resonator, Journal of Sound and Vibration. 205(2), pp. 151-165.
[3]. Truong. V.X, Chinh. N.D, Dien. K.D and Canh. T.V (2017), Closed-form Solutions to the 
Optimization of Dynamic Vibration Absorber Attached to Multi Degree-of-freedom Damped Linear 
Systems under Torsional Excitation using the Fxed-point Theory, Journal of Mutibody Dynamics 
(ISI), DOI: 10.1177/1464419317725216.
[4]. Truong. V.X, Dien. K.D, Chinh. N.D and Toan. N.D (2017), Optimal Parameters of Linear 
Dynamic Vibration Absorber for Reduction of Torsional Vibration, Journal of Science and 
Technology (Technical Universities), Vol 119, pp.37-42.
[5]. Khong Doan Dien, Vu Xuan Truong, Nguyen Duy Chinh (2017), The Fixed-points Theory for 
Shaft Model by Passive Mass-spring-disc Dynamic Vibration Absorber, Proceedings of The 2nd 
National Conference on Mechanical Engineering and Automation, ISBN 978-604-95-0221-7, pp. 
82-86.
ISSN 2354-0575
Khoa học & Công nghệ - Số 15/Tháng 9 - 2017 Journal of Science and Technology 33
[6]. Nguyễn Đông Anh, Nguyễn Bá Nghị (2006), Tính toán hệ TMD cho cơ hệ một bậc tự do nhằm 
giảm thành phần dao động tần số riêng, Luận văn Thạc sĩ, Đại học Bách khoa Hà Nội.
[7]. Nguyễn Duy Chinh, Vũ Xuân Trường, Khổng Doãn Điền (2017), Nghiên cứu thiết kế tối ưu bộ 
DVA giảm dao động xoắn cho trục máy theo phương pháp cực tiểu động năng của hệ, Tạp chí Kết 
cấu và Công nghệ Xây dựng, Hội Kết cấu và Công nghệ Xây dựng Việt Nam, Vol. 2.
A NUMERICAL STUDY ON THE VIBRATION OF THE SHAFT 
WITH TORSIONAL EXCITATION
Abtract:
The shaft is one of the most important parts of rotating machineries. Rotation of the shaft is 
commonly affected by torsional disturbances, which consequently excite the torsional vibration in the shaft. 
Such vibration causes fatigue damage and decreases overall performance of the shaft. One of the effective 
techniques to supress the harmful effect of torsional vibration is to use dynamic vibration absorbers (DVAs). 
This paper presents a numerical method for determining the vibration of a shaft subjected to harmonic, 
impact and random torsional excitations. 
Keywords: Torsional vibration, dynamic vibration absorber, harmonic excitation, impact excitation, 
random excitation.