Thiết kế mô phỏng bộ điều chế và giải điều chế vị trí xung hỗn loạn đa biểu tượng

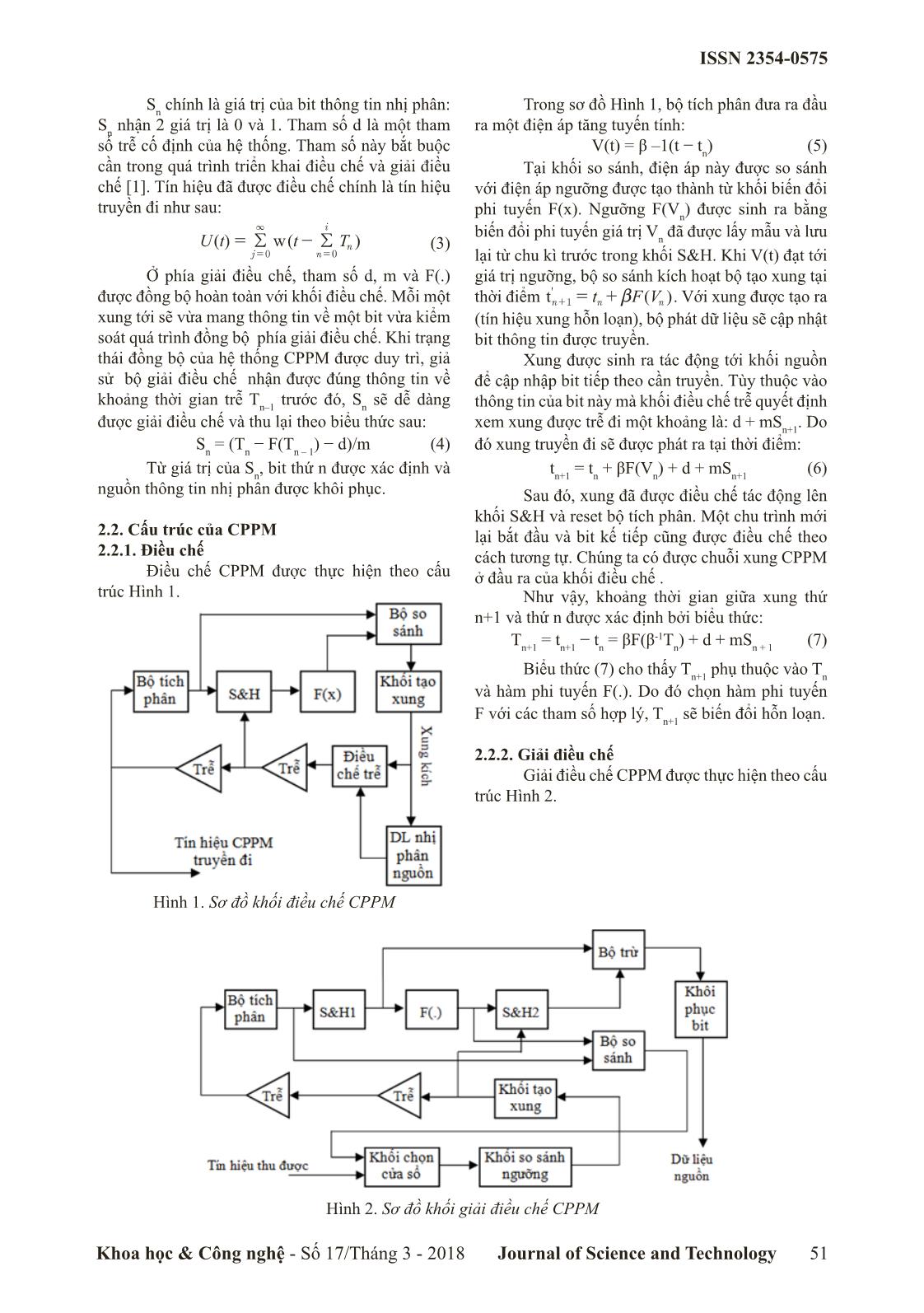
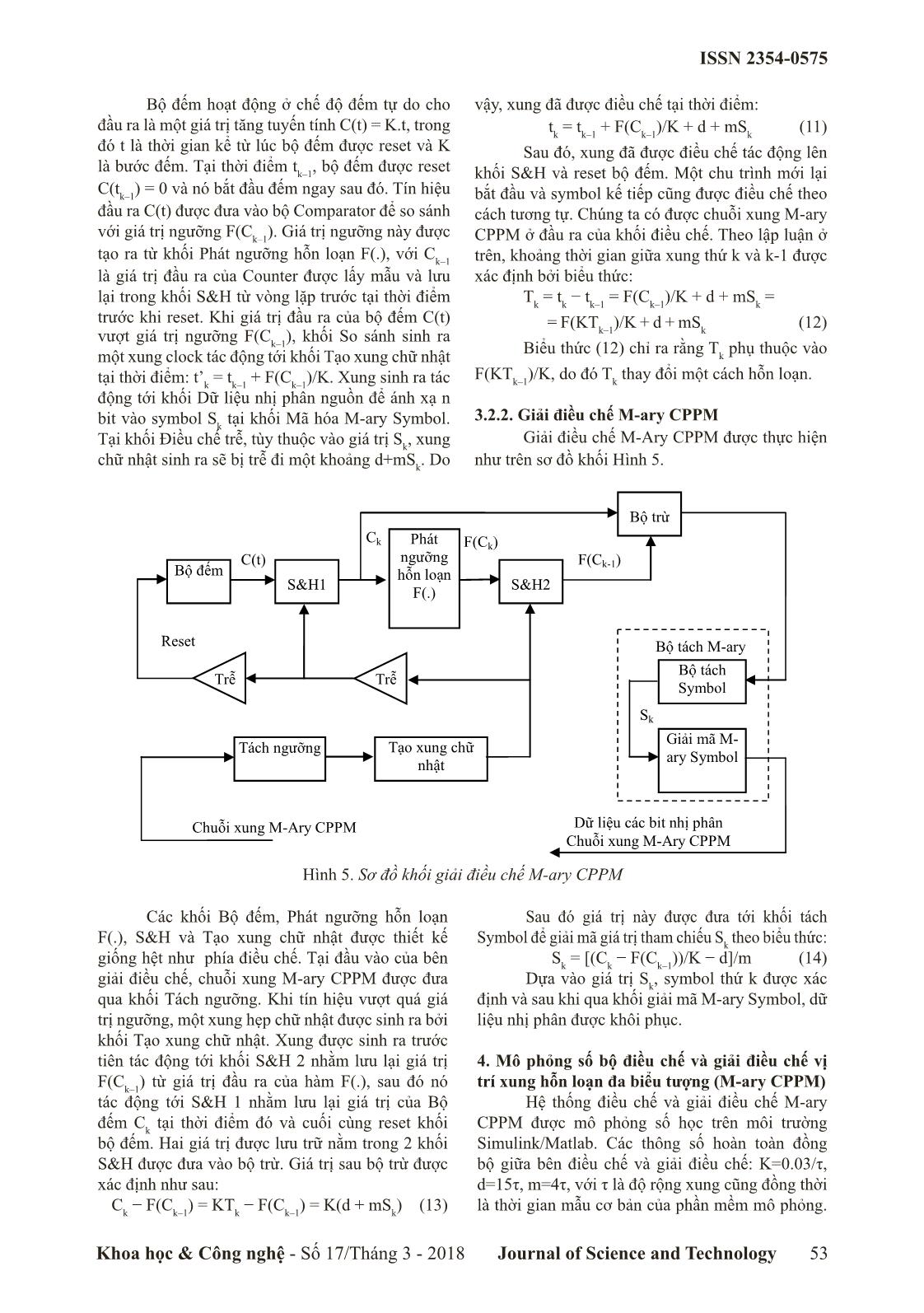
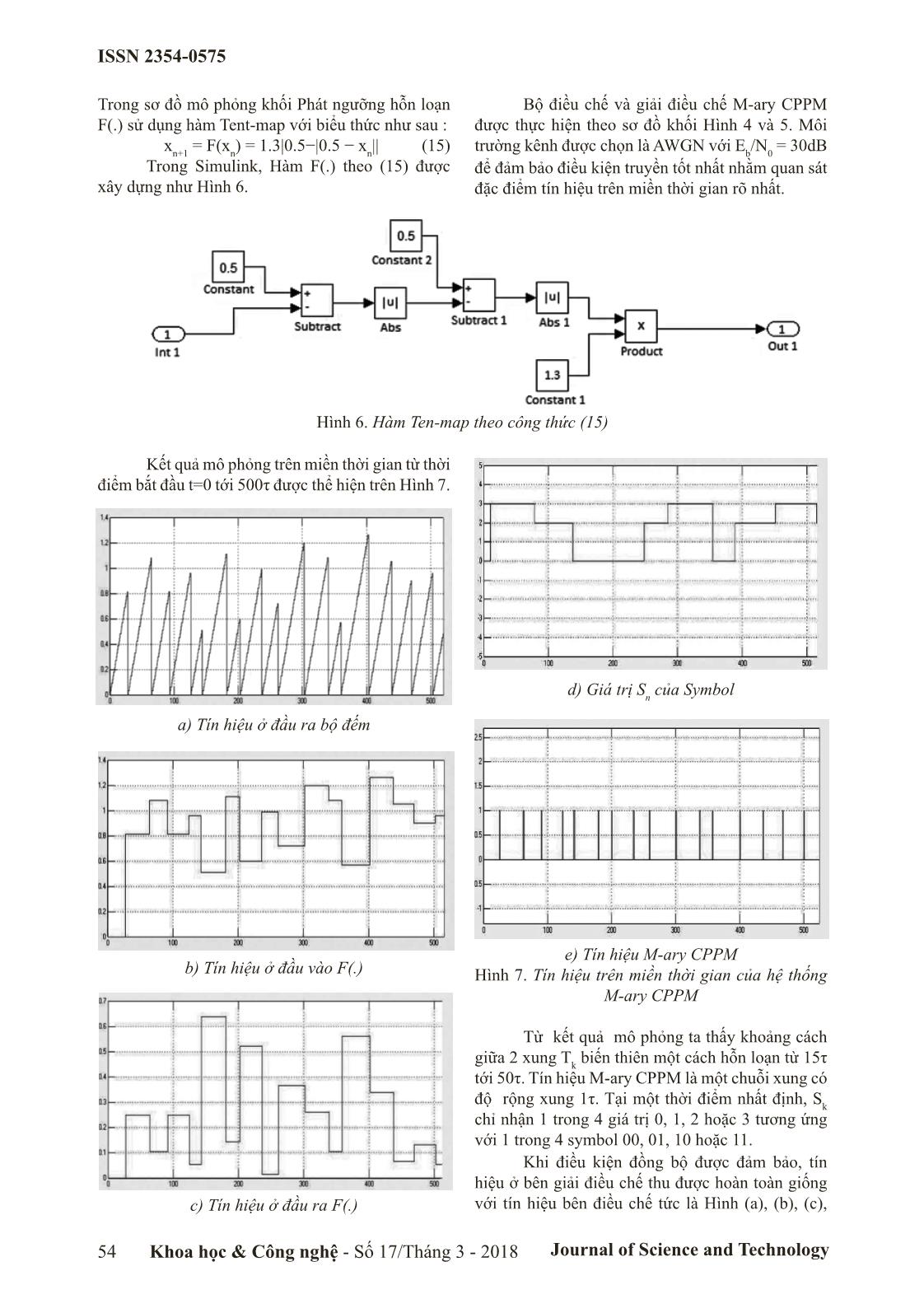
ị phân được khôi phục. Sau đó, xung đã được điều chế tác động lên 
 khối S&H và reset bộ tích phân. Một chu trình mới 
2.2. Cấu trúc của CPPM lại bắt đầu và bit kế tiếp cũng được điều chế theo 
2.2.1. Điều chế cách tương tự. Chúng ta có được chuỗi xung CPPM 
 Điều chế CPPM được thực hiện theo cấu ở đầu ra của khối điều chế . 
trúc Hình 1. Như vậy, khoảng thời gian giữa xung thứ 
 n+1 và thứ n được xác định bởi biểu thức: 
 -1
 Tn+1 = tn+1 − tn = βF(β Tn) + d + mSn + 1 (7)
 Biểu thức (7) cho thấy Tn+1 phụ thuộc vào Tn 
 và hàm phi tuyến F(.). Do đó chọn hàm phi tuyến 
 F với các tham số hợp lý, Tn+1 sẽ biến đổi hỗn loạn.
 2.2.2. Giải điều chế
 Giải điều chế CPPM được thực hiện theo cấu 
 trúc Hình 2.
 Hình 1. Sơ đồ khối điều chế CPPM
 Hình 2. Sơ đồ khối giải điều chế CPPM
Khoa học & Công nghệ - Số 17/Tháng 3 - 2018 Journal of Science and Technology 51
ISSN 2354-0575
 Trong sơ đồ Hình 2, các khối tích phân, với Tk là khoảng thời gian giữa xung thứ k và xung 
F(.), S&H và khối tạo xung được thiết kế giống hệt thứ k-1.
như phía điều chế. Tại đầu vào của bên giải điều 
chế, chuỗi xung CPPM được đưa qua khối so sánh 
ngưỡng. Khi tín hiệu vượt quá giá trị ngưỡng, một 
xung hẹp chữ nhật được sinh ra bởi khối này. Xung 
được sinh ra trước tiên tác động tới khối S&H 2 
nhằm lưu lại giá trị F(Vn) từ giá trị đầu ra của hàm 
F(.), sau đó nó tác động tới S&H 1 nhằm lưu lại giá 
trị của bộ tích phân lúc đó Vn+1 và cuối cùng reset 
bộ tích phân. Hai giá trị được lưu trữ nằm trong 
2 khối S&H được đưa vào bộ trừ. Giá trị sau bộ 
trừ nếu nhỏ hơn giá trị tham chiếu β(d+m/2) thì bit Hình 3. Tín hiệu M-ary CPPM
nhận được là 0, nếu lớn hơn giá trị tham chiếu thì 
bit nhận được là 1. Giá trị Tk là kết quả của hàm phi tuyến 
 Một phần quan trọng trong cơ chế này chính Tk=F(Tk-1) bằng cách chọn hàm phi tuyến F(.) với 
là khối chọn cửa sổ. Một khi bên giải điều chế thu các giá trị tham số thích hợp, Tk sẽ thay đổi một 
được 2 xung liên tiếp đúng, nó hoàn hoàn có thể dự cách hỗn loạn và như một giá trị ngẫu nhiên. Hình 
đoán được thời điểm sớm nhất mà xung tiếp theo 3 biểu diễn khoảng thời gian Tk trong trường hợp 
có thể đến. Điều đó có nghĩa là ta hoàn toàn có thể điều chế M mức.
đóng đầu vào của khối giải điều chế này cho tới Ở phía điều chế, thông tin nhị phân được 
trước thời điểm sớm nhất đó. Theo như sơ đồ thì điều chế lên tín hiệu sóng mang hỗn loạn nhờ cơ 
cửa sổ này sẽ được điều khiển bởi đầu ra của khối chế trễ như sau: 
so sánh. Cửa sổ này sẽ mở tại thời điểm: T = F(T ) + d + mS (10)
 ' k k – 1 k
 t(nn+1 =+tFb Vn ) (8)
 Trong đó Sk là giá trị tương ứng của symbol 
3. Điều chế vị trí xung hỗn loạn đa biểu tượng thứ k. Dữ liệu nguồn được nhóm thành từng nhóm 
(M-ary CPPM) nhiều bit và được ánh xạ tới các symbol tương ứng. 
 Dải giá trị của Sk tùy thuộc vào số bit trên mỗi 
 Khi sử dụng CPPM, với một tỉ số Eb/N0 đủ 
lớn thì hệ thống hoàn toàn đạt được BER tới 10-4. So symbol của phương pháp điều chế. Giả sử chúng ta 
với các hệ thống thông tin truyền thống thì không điều chế n bits/symbol, tương đương chúng ta sẽ có 
 M=2n symbols và S thay đổi từ 0 tới M−1.
cao hơn nhưng nếu so với các phương pháp điều k
chế khác trong truyền thông hỗn loạn thì đây rõ ràng 
là một điểm rất đáng chú ý. Tuy vậy, hệ thống lại có 3.2. Cấu trúc của M-ary CPPM
nhược điểm là tốc độ truyền thông tin chậm do mỗi 3.2.1. Điều chế M-ary CPPM
một xung nhận được chỉ giải mã được 1 bit. Rõ ràng Điều chế M-ary CPPM được thực hiện như 
đây là điều không hiệu quả về mặt truyền tin. trên sơ đồ khối Hình 4.
 Để giải quyết vấn đề này người ta đã phát Bộ so 
triển một phương pháp mới có tên gọi là M-ary sánh 
 C(t) 
 F(C ) 
CPPM. Đây là sự kết hợp của CPPM và điều chế đa Ck k
biểu tượng sẽ mang lại các ưu điểm: tiêu thụ năng Phát ngưỡng 
 Bộ đếm Clock
lượng thấp, tránh được hiệu ứng fading đa đường, ít S&H hỗn loạn F(.) 
gây ảnh hưởng tới các hệ thống khác, có tính riêng 
tư và bảo mật rất cao.
3.1. Nguyên lý của M-ary CPPM Bộ điều chế M-
 Giả thiết tín hiệu M-ary CPPM là một chuỗi ary CPPM 
xung chữ nhật hỗn loạn được minh họa như trên Điều chế Tạo xung 
Hình 3 và tuân theo biểu thức sau: Trễ trễ chữ nhật 
 3
 St()=-/ Au()ttkk--ut()t - x (9) S 
 k = 0 7A k n bits 
trong đó: u(t)=1 khi t ≥ 0 và u(t)=0 khi t < 0 là hàm Tín hiệu M-ary Mã hóa M- DL nhị 
bước nhảy đơn vị; A và τ lần lượt là biên độ và độ CPPM ary phân 
rộng của xung chữ nhật. Xung thứ k được sinh ra Symbol nguồn 
tại thời điểm:
 k
 ttkk=+0 / k = 0 T Hình 4. Sơ đồ khối điều chế M-ary CPPM
52 Khoa học & Công nghệ - Số 17/Tháng 3 - 2018 Journal of Science and Technology
 ISSN 2354-0575
 Bộ đếm hoạt động ở chế độ đếm tự do cho vậy, xung đã được điều chế tại thời điểm:
đầu ra là một giá trị tăng tuyến tính C(t) = K.t, trong 
 tk = tk–1 + F(Ck–1)/K + d + mSk (11)
đó t là thời gian kể từ lúc bộ đếm được reset và K Sau đó, xung đã được điều chế tác động lên 
là bước đếm. Tại thời điểm t , bộ đếm được reset 
 k–1 khối S&H và reset bộ đếm. Một chu trình mới lại 
C(tk–1) = 0 và nó bắt đầu đếm ngay sau đó. Tín hiệu bắt đầu và symbol kế tiếp cũng được điều chế theo 
đầu ra C(t) được đưa vào bộ Comparator để so sánh cách tương tự. Chúng ta có được chuỗi xung M-ary 
với giá trị ngưỡng F(Ck–1). Giá trị ngưỡng này được CPPM ở đầu ra của khối điều chế. Theo lập luận ở 
tạo ra từ khối Phát ngưỡng hỗn loạn F(.), với Ck–1 trên, khoảng thời gian giữa xung thứ k và k-1 được 
là giá trị đầu ra của Counter được lấy mẫu và lưu xác định bởi biểu thức:
lại trong khối S&H từ vòng lặp trước tại thời điểm Tk = tk − tk–1 = F(Ck–1)/K + d + mSk = 
trước khi reset. Khi giá trị đầu ra của bộ đếm C(t) = F(KT )/K + d + mS (12)
vượt giá trị ngưỡng F(C ), khối So sánh sinh ra k–1 k
 k–1 Biểu thức (12) chỉ ra rằng T phụ thuộc vào 
một xung clock tác động tới khối Tạo xung chữ nhật k
 F(KT )/K, do đó T thay đổi một cách hỗn loạn.
tại thời điểm: t’k = tk–1 + F(Ck–1)/K. Xung sinh ra tác k–1 k
động tới khối Dữ liệu nhị phân nguồn để ánh xạ n 
 3.2.2. Giải điều chế M-ary CPPM
bit vào symbol Sk tại khối Mã hóa M-ary Symbol. 
 Giải điều chế M-Ary CPPM được thực hiện 
Tại khối Điều chế trễ, tùy thuộc vào giá trị Sk, xung 
chữ nhật sinh ra sẽ bị trễ đi một khoảng d+mSk. Do như trên sơ đồ khối Hình 5.
 Bộ trừ 
 C 
 k Phát F(Ck) 
 C(t) ngưỡng F(Ck-1) 
 Bộ đếm hỗn loạn 
 S&H1 S&H2 
 F(.) 
 Reset Bộ tách M-ary 
 Bộ tách 
 Trễ Trễ 
 Symbol 
 Sk 
 Giải mã M-
 Tách ngưỡng Tạo xung chữ 
 ary Symbol 
 nhật 
 Chuỗi xung M-Ary CPPM Dữ liệu các bit nhị phân 
 Chuỗi xung M-Ary CPPM 
 Hình 5. Sơ đồ khối giải điều chế M-ary CPPM
 Các khối Bộ đếm, Phát ngưỡng hỗn loạn Sau đó giá trị này được đưa tới khối tách 
F(.), S&H và Tạo xung chữ nhật được thiết kế Symbol để giải mã giá trị tham chiếu Sk theo biểu thức:
giống hệt như phía điều chế. Tại đầu vào của bên Sk = [(Ck − F(Ck–1))/K − d]/m (14)
giải điều chế, chuỗi xung M-ary CPPM được đưa Dựa vào giá trị Sk, symbol thứ k được xác 
qua khối Tách ngưỡng. Khi tín hiệu vượt quá giá định và sau khi qua khối giải mã M-ary Symbol, dữ 
trị ngưỡng, một xung hẹp chữ nhật được sinh ra bởi liệu nhị phân được khôi phục.
khối Tạo xung chữ nhật. Xung được sinh ra trước 
tiên tác động tới khối S&H 2 nhằm lưu lại giá trị 4. Mô phỏng số bộ điều chế và giải điều chế vị 
F(Ck–1) từ giá trị đầu ra của hàm F(.), sau đó nó trí xung hỗn loạn đa biểu tượng (M-ary CPPM)
tác động tới S&H 1 nhằm lưu lại giá trị của Bộ Hệ thống điều chế và giải điều chế M-ary 
đếm Ck tại thời điểm đó và cuối cùng reset khối CPPM được mô phỏng số học trên môi trường 
bộ đếm. Hai giá trị được lưu trữ nằm trong 2 khối Simulink/Matlab. Các thông số hoàn toàn đồng 
S&H được đưa vào bộ trừ. Giá trị sau bộ trừ được bộ giữa bên điều chế và giải điều chế: K=0.03/τ, 
xác định như sau: d=15τ, m=4τ, với τ là độ rộng xung cũng đồng thời 
 Ck − F(Ck–1) = KTk − F(Ck–1) = K(d + mSk) (13) là thời gian mẫu cơ bản của phần mềm mô phỏng. 
Khoa học & Công nghệ - Số 17/Tháng 3 - 2018 Journal of Science and Technology 53
ISSN 2354-0575
Trong sơ đồ mô phỏng khối Phát ngưỡng hỗn loạn Bộ điều chế và giải điều chế M-ary CPPM 
F(.) sử dụng hàm Tent-map với biểu thức như sau : được thực hiện theo sơ đồ khối Hình 4 và 5. Môi 
 xn+1 = F(xn) = 1.3|0.5−|0.5 − xn|| (15) trường kênh được chọn là AWGN với Eb/N0 = 30dB 
 Trong Simulink, Hàm F(.) theo (15) được để đảm bảo điều kiện truyền tốt nhất nhằm quan sát 
xây dựng như Hình 6. đặc điểm tín hiệu trên miền thời gian rõ nhất.
 Hình 6. Hàm Ten-map theo công thức (15)
 Kết quả mô phỏng trên miền thời gian từ thời 
điểm bắt đầu t=0 tới 500τ được thể hiện trên Hình 7.
 d) Giá trị Sn của Symbol
 a) Tín hiệu ở đầu ra bộ đếm
 e) Tín hiệu M-ary CPPM
 b) Tín hiệu ở đầu vào F(.) Hình 7. Tín hiệu trên miền thời gian của hệ thống 
 M-ary CPPM
 Từ kết quả mô phỏng ta thấy khoảng cách 
 giữa 2 xung Tk biến thiên một cách hỗn loạn từ 15τ 
 tới 50τ. Tín hiệu M-ary CPPM là một chuỗi xung có 
 độ rộng xung 1τ. Tại một thời điểm nhất định, Sk 
 chỉ nhận 1 trong 4 giá trị 0, 1, 2 hoặc 3 tương ứng 
 với 1 trong 4 symbol 00, 01, 10 hoặc 11.
 Khi điều kiện đồng bộ được đảm bảo, tín 
 hiệu ở bên giải điều chế thu được hoàn toàn giống 
 c) Tín hiệu ở đầu ra F(.) với tín hiệu bên điều chế tức là Hình (a), (b), (c), 
54 Khoa học & Công nghệ - Số 17/Tháng 3 - 2018 Journal of Science and Technology
 ISSN 2354-0575
(d) và (e) cũng đồng thời mô tả tín hiệu trên miền Bảng 1 thể hiện sự so sánh tốc độ truyền 
thời gian ở các khối trong giải điều chế. Điều này 2,4,8,16 CPPM trong quá trình mô phỏng trên 
chứng tỏ điều chế M-ary CPPM là hoàn toàn hợp lí 10000 mẫu thời gian trên cùng một tỉ số Eb/N0. Kết 
và khả thi. quả cho thấy M-ary CPPM tuy đạt tốc độ xung thấp 
 Để đánh giá hiệu quả của giải pháp trên ta hơn một chút so với CPPM nhưng lại có tốc độ 
xem xét tỉ số lỗi của 2,4,8,16-ary CPPM qua tính bit truyền cao hơn đáng kể so với CPPM. Kết quả 
toán mô phỏng số. Trong hệ thống, ở phía đầu thu trên là vô cùng quan trọng và đã chứng minh được 
tín hiệu nhận được là tổng của tín hiệu chuỗi xung M-ary CPPM cải tiến được đáng kể tốc độ bit so 
M-ary CPPM truyền đi và nhiễu trắng AWGN. với CPPM.
Căn cứ vào sự so sánh mức tín hiệu nhận được với 
mức ngưỡng, máy thu sẽ quyết định đó là xung chữ 5. Kết luận
nhật hay không. Bảng 1 thống kê tốc độ truyền của Hỗn loạn là một lĩnh vực khoa học đầy tiềm 
M-ary CPPM được thực hiện với trên 10000 mẫu năng đang được nghiên cứu ứng dụng mạnh mẽ 
thời gian mô phỏng. trong truyền thông. Việc kết hợp với đa biểu tượng 
Bảng 1. Tốc độ truyền của M-ary CPPM trên 10000 thành phương pháp điều chế M-ary CPPM giúp cải 
 mẫu thời gian mô phỏng thiện tốc độ bit đáng kể so với phương pháp CPPM. 
 Cải tiến này cùng với các đặc tính của phương 
 M Số xung đã truyền Số bit đã truyền pháp như tính bảo mật cao, hoạt động tốt trong môi 
 2 3587 3587 trường nhiễu và méo, đạt được tỉ số lỗi bit ở mức 
 chấp nhận được so với các phương pháp điều chế 
 4 3225 6450 thông thường đã làm M-ary CPPM trở thành một 
 8 3166 9498 phương pháp có khả năng ứng dụng cao vào truyền 
 thông hỗn loạn, đặc biệt trong truyền thông băng 
 16 3112 12448
 siêu rộng.
Tai liêu tham khao
 [1]. Hoàng Mạnh Thắng, Vũ Văn Yêm, Nguyễn Tiến Dũng. Ứng dụng động học phi tuyến và hỗn 
 loạn trong truyền thông, NXB Bách khoa, 2012.
 [2]. S. H. Strogat. Nonlinear Dynamics And Chaos: With Applications To Physics, Biology, Chemistry, 
 And Engineering.: Westview Press, 2001.
 [3]. E. N. Lorenz, Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 1963, vol. 
 20, pp. 131-140.
 [4]. Z. Jákó and G. Kolumbán, Carrier generation for chaotic communication by fourth- order analog 
 phase-lock loop. In International Symposium on Nonlinear Theory and its Applications (NOLTA’98), 
 Crans-Montana, Switzerland, 1998, pp. 827-830.
 [5]. H. Dedieu and M. J. Ogorzalek, Nonlinear approach to signal coding and compression. In 
 European Conference on Circuit Theory and Design (ECCTD’99), Stresa-Italy, 1999, pp. 58-61.
 [6]. B. Chen and G. W. Wornell, Efficient channel coding for analog sources using chaotic systems. 
 In IEEE GLOBECOM, London-UK, 1996.
 [7]. D. R. Frey, Chaotic digital encoding: An approach to secure communication. IEEE Transactions 
 on Circuits and Systems II, 1993, vol. 40, no. 10, pp. 660-666.
 [8]. P. Stavroulakis. Chaos Applications in Telecommunications: CRC Press, 2005.
 [9]. F. C. M. Lau and C. K. Tse. Chaos-Based Digital Communication Systems: Operating Principles, 
 Analysis Methods, and Performance Evaluation: Springer, 2003.
 [10]. M. P. Kennedy and G. Kolumbán, Special issue on noncoherent chaotic communications. IEEE 
 Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, vol. 47, no. 
 12, pp. 1661–1662.
 [11]. A. Abel and W. Schwarz, Chaos communications-principles, schemes, and system analysis. 
 Proceedings of the IEEE, 2002, vol. 90, no. 5, pp. 691–710.
 [12]. H. Dedieu, M. P. Kennedy, and M. Hasler, Chaos shift keying: Modulation and demodulation 
 of a chaotic carrier using self-synchronizing Chua’s circuit. IEEE Transactions on Circuits and 
 Systems II, 1993, vol. 40, no. 10, pp. 634–642.
 [13]. G. Kolumbán, M. P. Kennedy, and L. O. Chua, The role of synchronization in digital 
Khoa học & Công nghệ - Số 17/Tháng 3 - 2018 Journal of Science and Technology 55
ISSN 2354-0575
 communications-Part II: Chaotic modulation and chaotic synchronization. IEEE Transactions on 
 Circuits and Systems I, 1998, vol. 45, no. 4, pp. 1129–1140.
 [14]. M. Sushchik, L.S. Tsimring, and A. R. Volkovskii, Performance analysis of correlation-based 
 communication schemes utilizing chaos. IEEE Transactions on Circuits and Systems I, 2000, vol. 
 47, no. 12, pp. 1684–1691.
 [15]. S. Boccaletti and et al., The synchronization of chaotic systems, I. Procaccia, Ed.Florence, 
 Italy: Elsevier Science, February 2002.
 DESIGN DEMONSTRATION M-ary
 CHAOTIC PULSE POSITION MODULATOR AND DEMODULATOR
Abstract:
 Chaotic phenomena have been known since the late 19th century but have only really received a 
strong research interest by the scientific community in recent years with a series of publications in which 
the field electronics and communications. Over the past two decades, research applications in this field 
have been dominated by three main directions: security, application in spread spectrum information and 
digital modulation/demodulation. This paper presents the design solution for simulating the number of 
application-specific pulses/pulse-position modulation emulation modulators used in multi-directional 
application in Ultra Wide Band communications. Simulation results will show improvement of the bit error 
rate over the interference channel, improving the security and feasibility of the solution.
Keywords: Chaotic, CPPM, UWB, Modulation.
56 Khoa học & Công nghệ - Số 17/Tháng 3 - 2018 Journal of Science and Technology