Simulation of reconfiguration system using matlab - Simulink environment
Reconfiguration strategy of solar energy has been a challenging task in the energy optimization field, in which the intention is to minimize losses and increase efficiency of the photovoltaic
(PV) system under non-homogeneous solar irradiation based on irradiance equalization. The reconfiguration system (RS) proposed includes: irradiance equalization algorithms which is effective in
the calculation to find an optimal configuration; dynamic electrical scheme (DES) switching matrix
which is controlled to obtain the optimal configuration for PV array. Recently, publications have
focused on bringing out the algorithms with the aim to select the optimal connection configuration
and control DES switching matrix. However, to our knowledge, there has been no published work
using Matlab-simulink to simulate the RS operation. The simulation enables researchers to perform
experiments and evaluate reconfiguration algorithms effectively before deploying in reality. In the
paper, we present a study on simulation of RS operation using Matlab-simulink environment. The
results show that, with RS, the effectiveness of the PV array performance can rise by 10-50%.

Trang 1

Trang 2
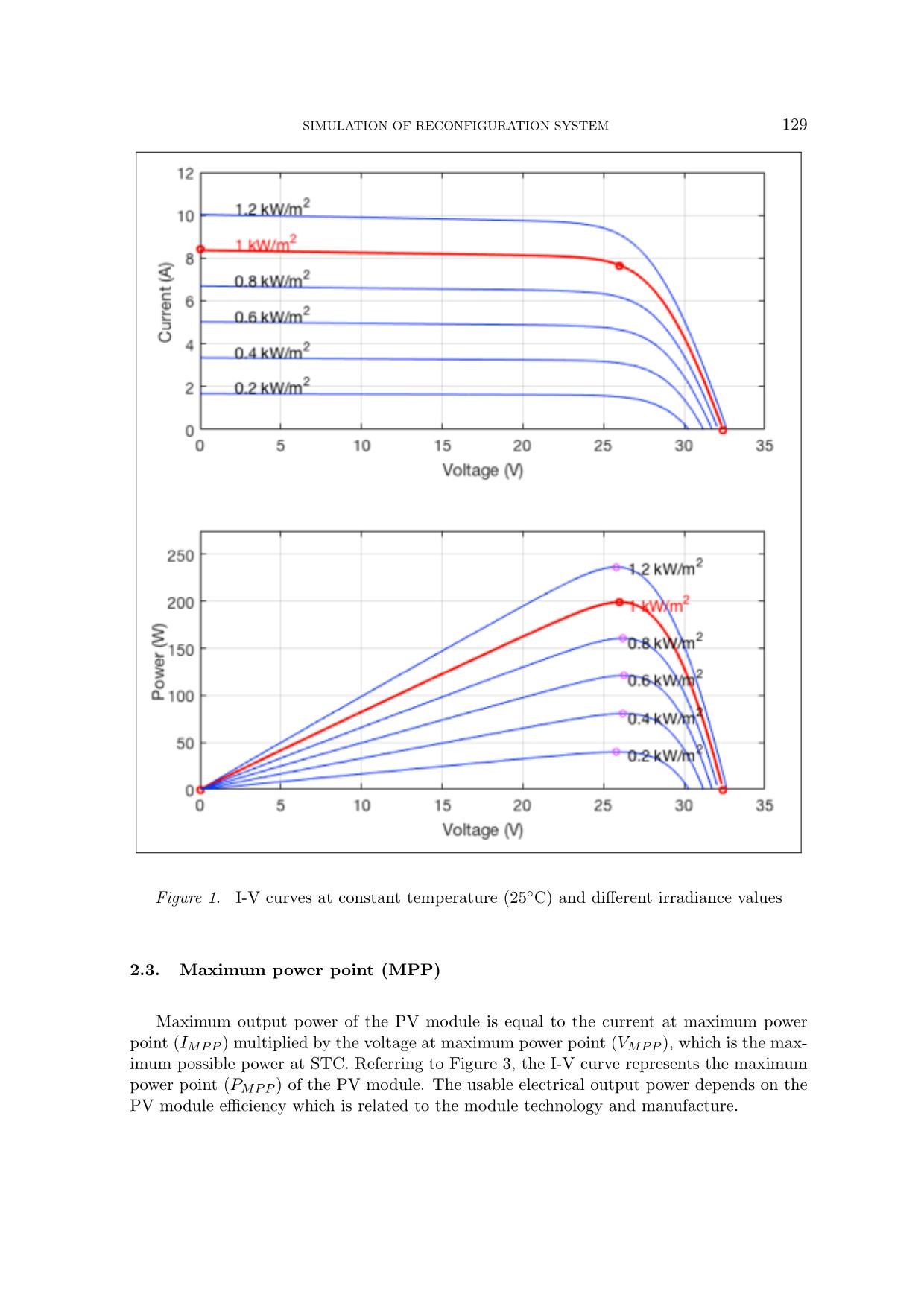
Trang 3
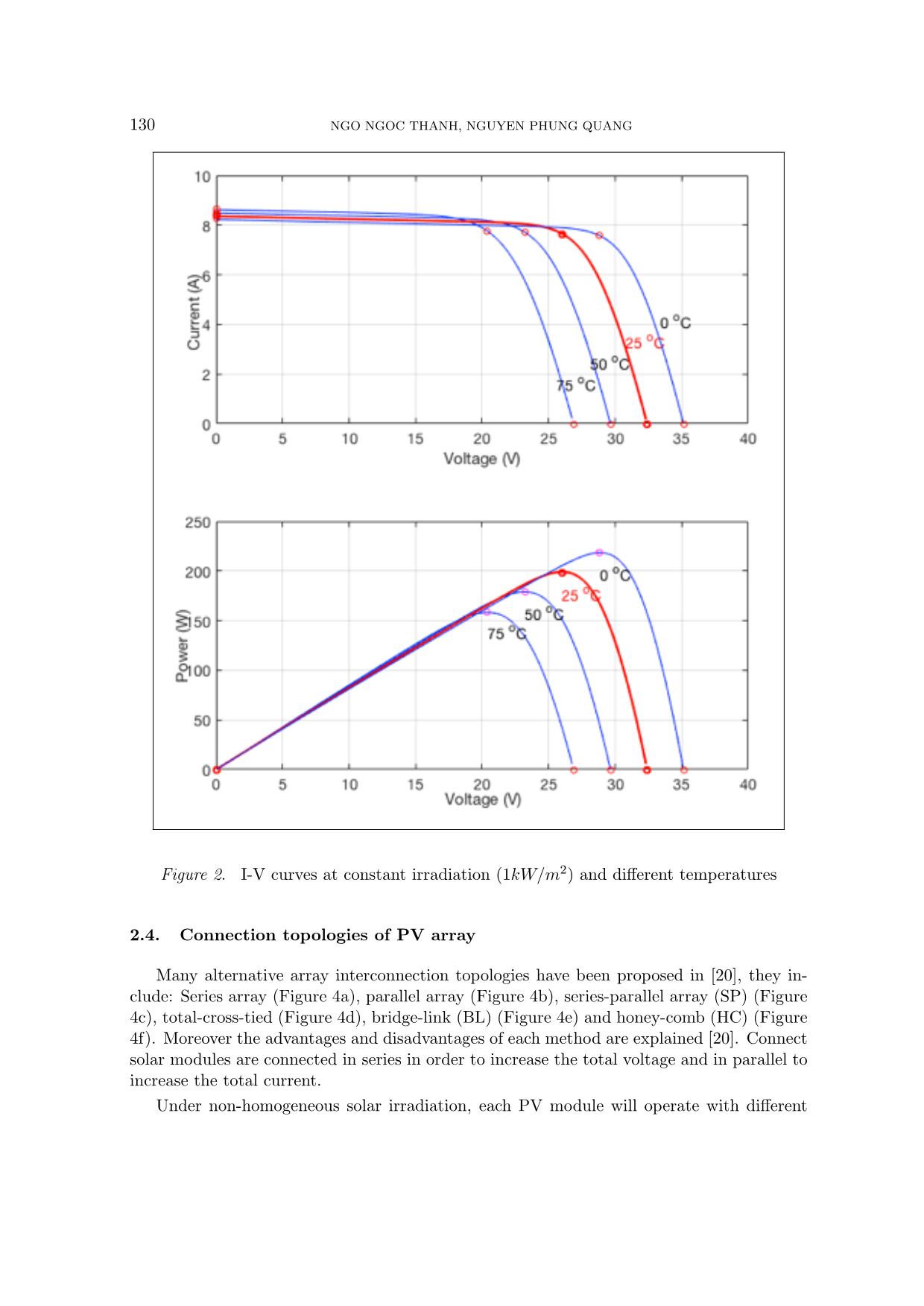
Trang 4
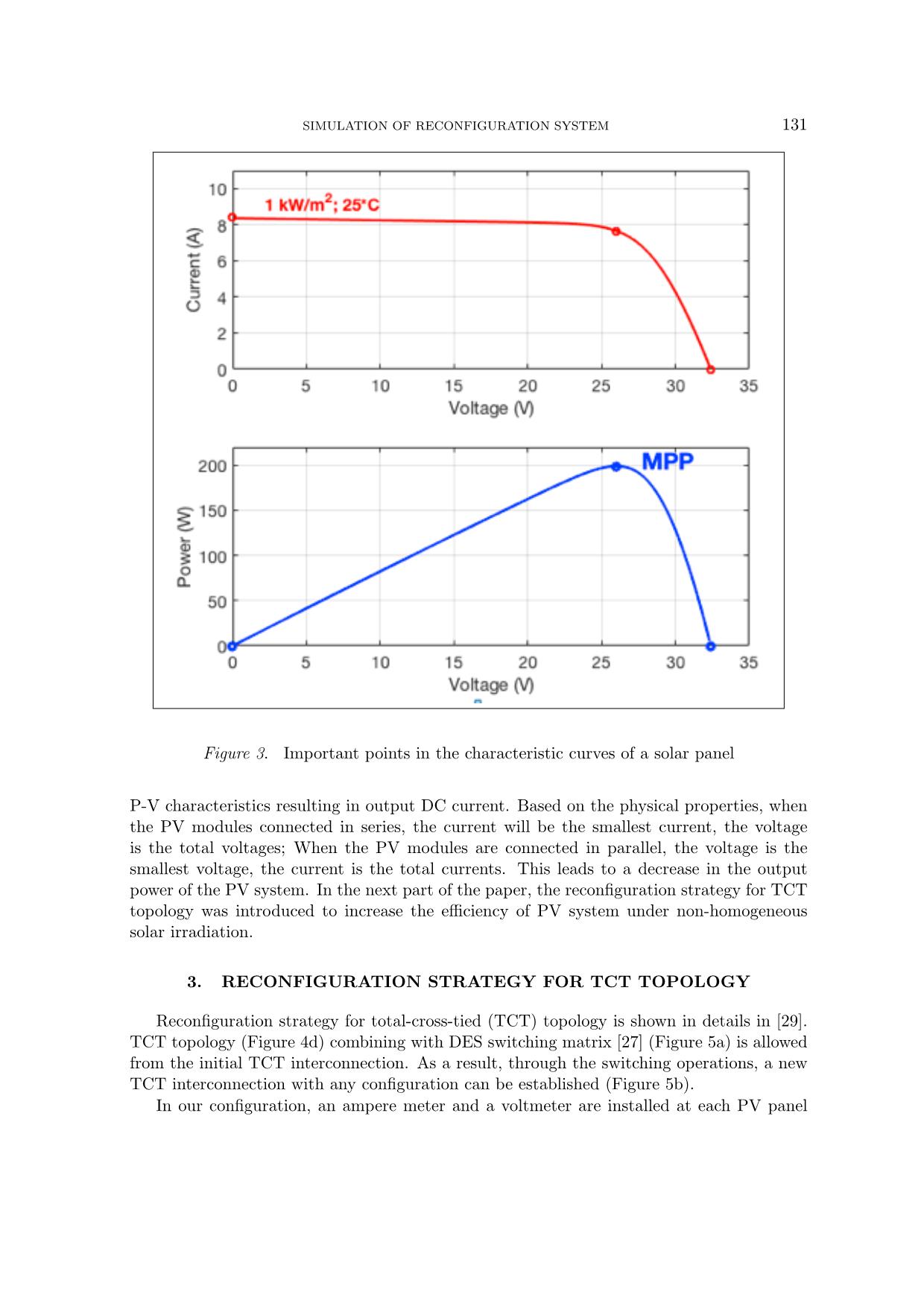
Trang 5

Trang 6

Trang 7
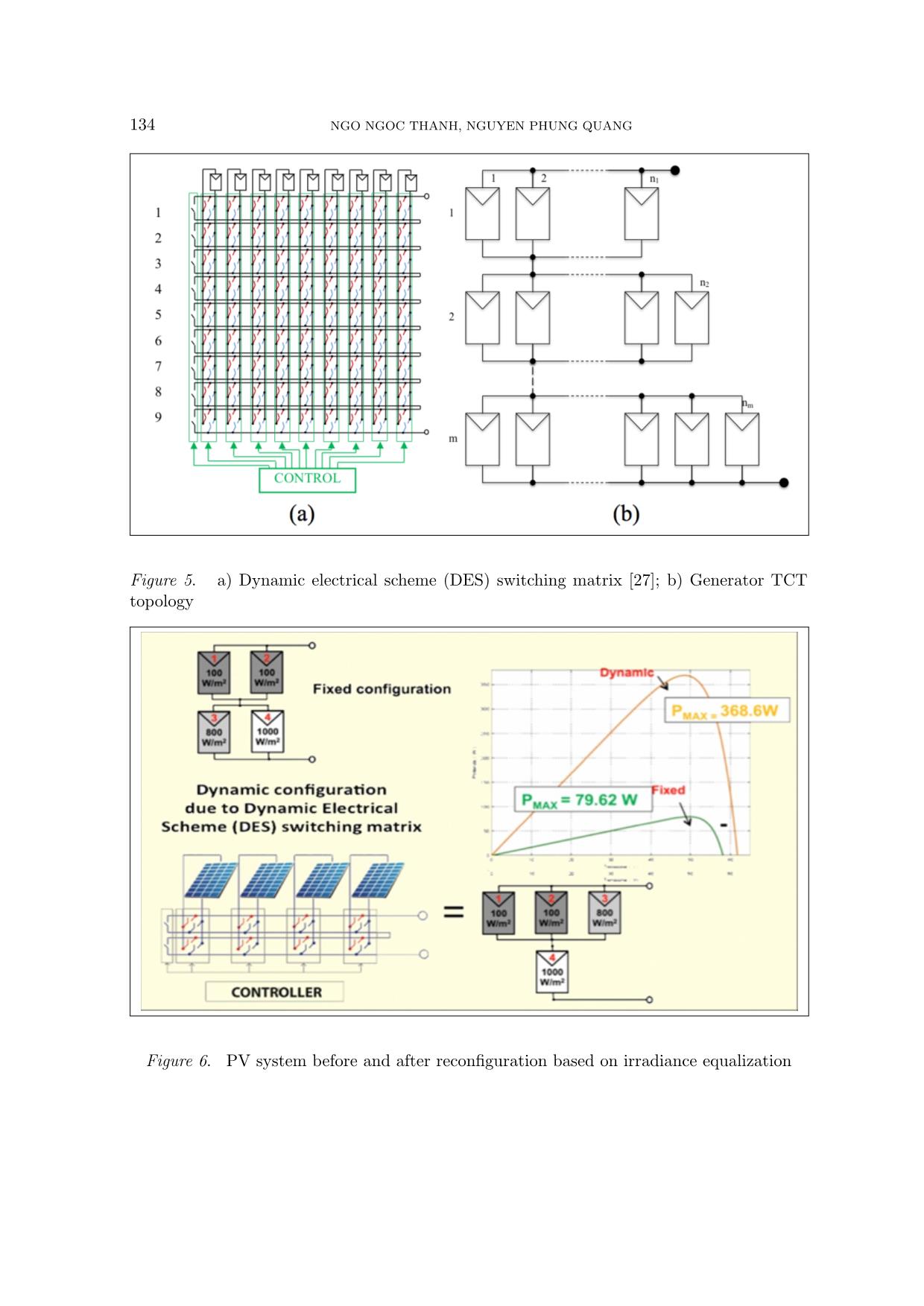
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Simulation of reconfiguration system using matlab - Simulink environment

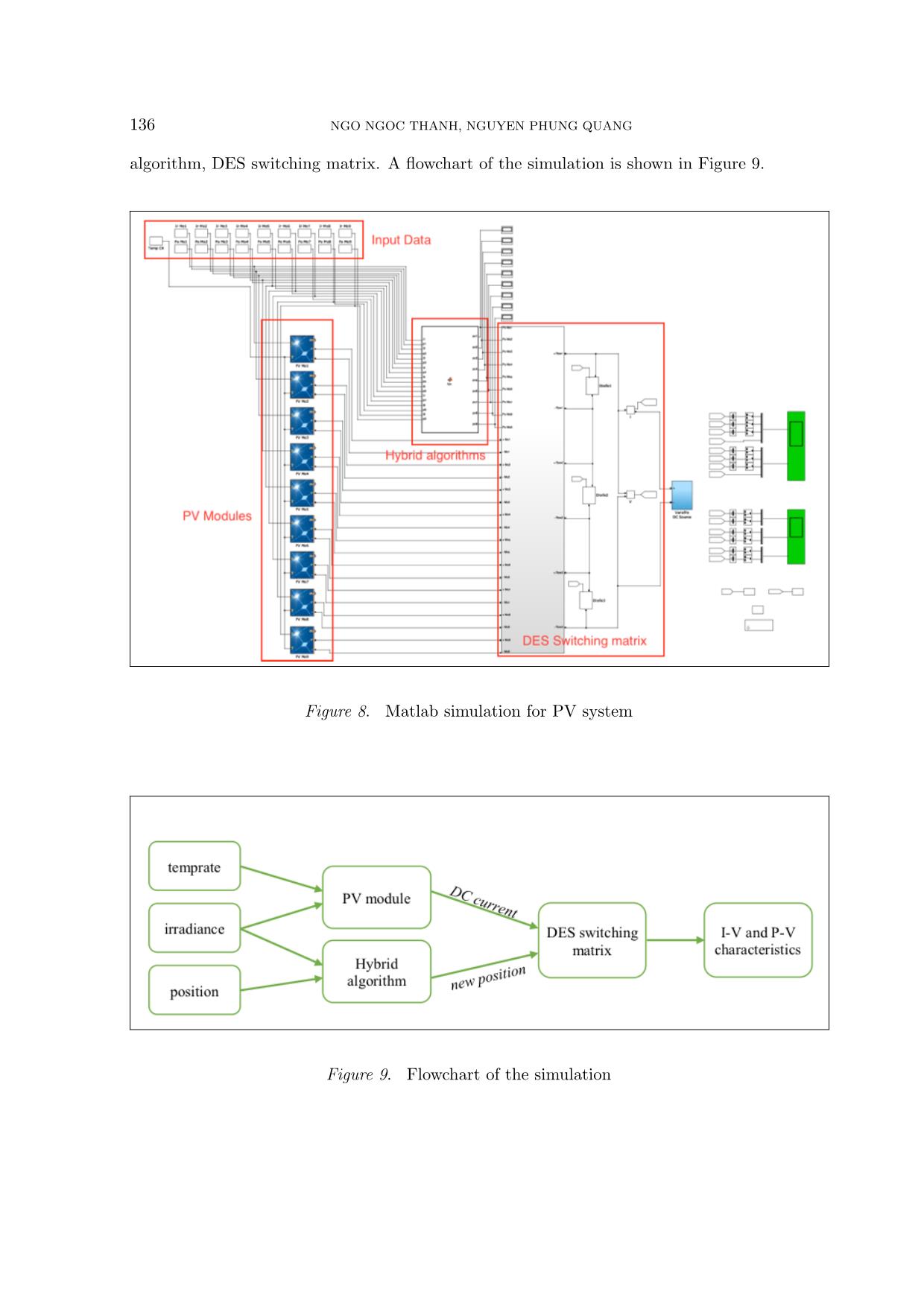
initial configuration, the P-V characteristic is green line with peak power at Pmax = 79.60W. By using the DES switching matrix and Controller, the PV system reconfiguration to optimal configuration by changing position of module 3 from row 2 to row 1. Then, the P-V characteristic of PV system is red line with peak power increase to Pmax = 368.6W . In order to find out the optimal configuration for PV array, we use a hybrid algorithm which is published in [22, 29]. Dynamic programming (DP) [29] is used for Subset Sum problem in “Knapsack problems”. DP technique assesses for each panel the power able to be supplied and inserts it into a dynamic array, which gives rise to the connections between panels. With an intelligent method, DP select panels with total irradiation that are equalization and then arrange them in a separated row. However, DP offers the best result in almost all cases, but in some special situations DP does not bring good results. Smart choice (SC) [22] proposed to overcome the special case of DP. Finally, SC combined with DP in order to create a hybrid algorithm and obtain better results as compared to established methods for irradiance equalization. Diagram of hybrid algorithm is shown in Figure 7. In the paper, we use Matlab-simulink environment to simulate the operation of RS for optimal PV array configuration. Simulation is executed on PV system including 9 PV mo- dules operating under non-homogeneous solar irradiance. Based on the irradiation received 134 NGO NGOC THANH, NGUYEN PHUNG QUANG Figure 5. a) Dynamic electrical scheme (DES) switching matrix [27]; b) Generator TCT topology Figure 6. PV system before and after reconfiguration based on irradiance equalization SIMULATION OF RECONFIGURATION SYSTEM 135 Figure 7. Hybrid algorithm from the PV modules, irradiance equalization algorithms as proposed can be used to find the optimal configuration. Consequently, the controller controlling DES switching matrix reconfiguration PV system from initial configuration to optimal configuration, PV system will operate at maximum power. 4. MATLAB SIMULATION There have been several publications using Matlab-Simulink to simulate PV module operation under non-homogeneous solar irradiance [1, 5, 8, 9, 17, 24, 28] which mainly focus on the simulation of PV module operation, thereby graphing features I-V and P-V. In this part, we mainly focus on simulation of RS to verify behavior of the system. Hence, we do not focus on how to simulate PV module under non-homogeneous solar radiation, we use the result of “partial shading of a PV module” in [21] for simulating PV module operation. Matlab simulation (Figure 8) includes four main parts: input data; PV modules, hybrid 136 NGO NGOC THANH, NGUYEN PHUNG QUANG algorithm, DES switching matrix. A flowchart of the simulation is shown in Figure 9. Figure 8. Matlab simulation for PV system Figure 9. Flowchart of the simulation SIMULATION OF RECONFIGURATION SYSTEM 137 4.1. PV module It is the result of PV module simulation under conditions of non-homogeneous irradiance at [21], the PV module with the input data being irradiance (W/m2) and temperature (◦C); and the output data being DC current (+ and -). The model parameter is selected as in the standard PV module data-sheet parameter: ISC , VOC , rated current IR at MPP and rated voltage VR at MPP under standard test conditions (1kW/m 2, 25◦C) (Figure 10). Figure 10. Parameters of PV module Figure 11. Schematic design of DES switching matrix When the PV system operates under conditions of non-homogeneous solar irradiance, depending on the irradiance level received, each PV module brings forward a different DC current. In this simulation, we focus on the PV system working at non-homogeneous irradi- ance, hence we chose the ideal condition for PV modules is 25◦C. 138 NGO NGOC THANH, NGUYEN PHUNG QUANG Figure 12. DES switching matrix Figure 13. Input data for simulation SIMULATION OF RECONFIGURATION SYSTEM 139 4.2. Hybrid algorithm In this section, we modelize hybrid algorithm in a Matlab function block. The main aim of the hybrid algorithm is to seek the optimal connection configuration of the system to archive the best performance. The hybrid algorithm is shown in Figure 7. The input data of the hybrid algorithm are irradiances and positions of each PV module. The result is the optimal configuration: new position of each PV module on each parallel connection in TCT topology. 4.3. DES switching matrix Figure 11 demonstrates a schematic design of the DES switching matrix designed for 9 PV modules. Each PV module is connected into three rows via switches. It can change the Figure 14. PV system before reconfiguration (a-c) and after reconfiguration with RS (b-d) 140 NGO NGOC THANH, NGUYEN PHUNG QUANG position of the connection between the rows. Switching from row x to row y can be done by opening switch at row x and closing switch at row y. For example, PV module want to connect to row 1: switches in row 2 and 3 are open, switch in row 1 is close. Through opening/closing the switches in DES, PV system can change the configuration from the initial TCT topology to any TCT topology with up to three rows. Figure 12 is an illustration of the basis of schematic design in Matlab-simulink environ- ment with the input data for each PV module as: DC current and the new position after the reconfiguration. DES switching matrix is restructured within three circuits connected in parallel to ensure the input assumptions for the inverters. Based on the new position of each PV module, the controller is able to control ideal switches for the corresponding connection configuration. The result of the DES switching matrix is DC currents of the PV system. 4.4. Result of simulation Simulation with 9 PV modules is connected as shown in Figure 14a. At the initial configuration, the PV modules received different irradiance. Hence, total irradiation in the parallel circuit is different. The I-V and P-V characteristics of the system before the reconfiguration with Pmax = 791.1W is demonstrated in Figure 14c. With PV system as seen in Figure 14a (input data of Matlab simulation show in Figure 13), the hybrid algorithm provides an optimal PV configuration. Then, DES switching matrix used the result of hybrid algorithm to change the connection of PV system from initial configuration to the optimal configuration (Figure 14b with irradiance equalization on each row of PV system). The position of PV modules 7, 4, 6, 3 has changed. After using the reconfiguration system, P-V characteristics (Figure 14d) have been improved markedly with Pmax = 1079W (performance increases by 29%). 5. CONCLUSIONS A Matlab/Simulink software has been developed to simulate the behavior of PV modules with different configurations under non-homogeneous of solar irradiance. The effect of the reconfiguration system on PV characteristics under partially shaded conditions has been modelized in the study. Additionally, an experimental measurement has been performed and validity of the simulation software has been verified. The results show that the software is a promising tool for further research on the effectiveness of reconfiguration algorithms in solar power plant. REFERENCES [1] “Pv module simulink models,” ECEN 2060 Renewable Sources and Efficient Electrical Energy Systems. [Online]. Available: [online]Available:∼ecen2060/materials/ simulink/PV/PV module model.pdf [2] “Electricity from sunlight: an introduction to photovoltaics,” Choice: Current Reviews for Aca- demic Libraries, vol. 48, no. 5, pp. 933–933, 2011. [3] “Trends in photovoltaic applications. survey report of selected iea countries between 1992 and 2012,” Report, 2013. SIMULATION OF RECONFIGURATION SYSTEM 141 [4] M. Alahmada, M. A. Chaabanb, S. kit Laua, J. Shic, and J. Neald, “An adaptive utility in- teractive photovoltaic system based on a flexible switch matrix to optimize performance in real-time,” Solar Energy, vol. 86, p. 951963, 2012. [5] B. A. Alsayid, S. Y. Alsadi, J. S. Jallad, and M. H. Dradi, “Partial shading of pv system simulation with experimental results,” Smart Grid and Renewable Energy, vol. 4, pp. 429–435, 2013. [6] M. Balato, L. Costanzo, and M. Vitelli, “Maximum power point tracking techniques,” Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 1–26, 2016. [7] F. Belhachata and C. Larbesb, “Modeling, analysis and comparison of solar photovoltaic array configurations under partial shading conditions,” Solar Energy, vol. 120, p. 399418, 2015. [8] N. Belhaouas, M. A. Cheikh, A. Malek, and C. Larbes, “Matlab-simulink of photovoltaic system based on a two-diode model simulator with shaded solar cells,” Revue des Energies Renouvelables, vol. 16, pp. 65–73, 2013. [9] U. S. Bhadoria and R. Narvey, “Modeling and simulation of pv arrays under psc (partial shading conditions),” International Journal of Electronic and Electrical Engineering, vol. 7, pp. 423–430, 2014. [10] P.-C. Chena, P.-Y. Chena, Y.-H. Liua, J.-H. Chena, and Y.-F. Luob, “A comparative study on maximum power point tracking techniques for photovoltaic generation systems operating under fast changing environments,” Solar Energy, vol. 119, p. 261276, 2015. [11] C. Delinea, A. Dobosa, S. Janzoua, J. Meydbrayb, and M. Donovanb, “A simplified model of uniform shading in large photovoltaic arrays,” Solar Energy, vol. 96, p. Pages 274282, 2013. [12] M. Z. S. El-Dein, M. Kazerani, and M. M. A. Salama, “Optimal photovoltaic array reconfigura- tion to reduce partial shading losses,” IEEE Transactions on Sustainable Energy, vol. 4, no. 1, p. 9, 2012. [13] N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli, Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic systems, 2012. [14] M. C. A. Garcia, W. Herrmann, W. Bohmer, and B. Proisy, “Thermal and electrical effects cau- sed by outdoor hot-spot testing in associations of photovoltaic cells,” Progress in Photovoltaics, vol. 11, no. 5, pp. 293–307, 2003. [15] N. Gokmena, E. Karatepea, F. Ugranlia, and S. Silvestreb, “Voltage band based global mppt controller for photovoltaic systems,” Solar Energy, vol. 98, Part C, p. 322334, 2013. [16] S. GS, D. V. P, M. G, P. D, and M. A, “A review of ir thermography applied to pv systems,” Environment and Electrical Engineering (EEEIC), 2012 Eleventh international conference, 2012. [17] C. Keles, B. B. Alagoz, M. Akcin, A. Kaygusuz, and A. Karabiber, “A photovoltaic system model for matlab/simulink simulations,” 4th International Conference on Power Engineering, 2013. [18] A. Kouchaki, H. Iman-Eini, and B. Asaei, “A new maximum power point tracking strategy for pv arrays under uniform and non-uniform insolation conditions,” Solar Energy, vol. 91, p. 221232, 2013. 142 NGO NGOC THANH, NGUYEN PHUNG QUANG [19] Y.-H. Liua, J.-H. Chena, and J.-W. Huangb, “Global maximum power point tracking algorithm for pv systems operating under partially shaded conditions using the segmentation search met- hod,” Solar Energy, vol. 103, p. 350363, 2014. [20] D. L. Manna, V. L. Vigni, E. R. Sanseverino, V. D. Dio, and P. Romano, “Reconfigurable elec- trical interconnection strategies for photovoltaic arrays: A review,” Renewable and Sustainable Energy Reviews, 2014. [21] MathWorks, “Partial shading of a pv module,” /examples/partial-shading-of-a-pv-module.html. [22] T. N. Ngoc, Q. N. Phung, L. N. Tung, E. R. Sanseverino, P. Romano, and F. Viola, “Increa- sing efficiency of photovoltaic systems under non-homogeneous solar irradiation using improved dynamic programming methods,” Solar Energy, vol. 150, pp. 325–334, 2017. [23] D. Nguyen and B. Lehman, “An adaptive solar photovoltaic array using model-based reconfiguration algorithm,” Ieee Transactions on Industrial Electronics, vol. 55, no. 7, pp. 2644–2654, 2008. [Online]. Available: 〈GotoISI〉://WOS:000257582900010 [24] X. H. Nguyen, “Matlab/simulink based modeling to study effect of partial shadow on solar photovoltaic array,” Environmental Systems Research, 2015. [25] H. Obane, K. Okajima, T. Oozeki, and T. Ishii, “Pv system with reconnection to improve output under nonuniform illumination,” IEEE Journal of Photovoltaics, vol. 2, no. 3, pp. 341–347, 2012. [26] G. V. Quesada, J. J. N. Vera, F. G. Gispert, and R. Pique, “Irradiance equalization method for output power optimization in plant oriented grid-connected pv generators,” Power Electronics and Applications, 2005 European Conference on, pp. 10, P.10, 2005. [27] P. Romano, R. Candela, M. Cardinale, V. L. Vigni, D. Musso, and E. R. Sanseverino, “Opti- mization of photovoltaic energy production through an efficient switching matrix,” Journal of Sustainable Development of Energy, Water and Environment Systems, vol. 1, no. 3, pp. 227–236, 2013. [28] S. Said, A. Massoud, M. Benammar, and S. Ahmed, “A matlab/simulink-based photovoltaic array model employing simpowersystems toolbox,” Journal of Energy and Power Engineering, vol. 6, pp. 1965–1975, 2012. [29] E. R. Sanseverino, N. N. Thanh, M. Cardinale, V. L. Vigni, D. Musso, P. Romano, and F. Viola, “Dynamic programming and munkres algorithm for optimal photovoltaic arrays reconfiguration,” Solar Energy, vol. 122, p. Pages 347358, 12/2015. [30] S. Silvestre, A. Boronat, and A. Chouder, “Study of bypass diodes configuration on pv modules,” Applied Energy, vol. 86, no. 9, pp. 1632–1640, 2009. [31] J. Storey, P. Wilson, and D. Bagnall, “Improved optimization strategy for irradiance equalization in dynamic photovoltaic arrays,” Power Electronics, IEEE Transactions on, vol. 28, no. 6, p. 11, 2012. [32] Uezato, M. Veerachary, and T. Senjyu, “Voltage-based maximum power point tracking control of pv system,” IEEE Transactions on Aerospace and Electronic Systems, vol. 38, no. 1, pp. 262 – 270, Jan 2002. SIMULATION OF RECONFIGURATION SYSTEM 143 [33] G. Velasco, F. Guinjoan, and R. Pique, “Electrical pv array reconfiguration strategy for energy extraction improvement in grid-connected pv systems,” Ieee Transactions on Industrial Electronics, vol. 56, no. 11, pp. 4319–4331, 2009. [Online]. Available: 〈GotoISI〉://WOS:000270720100003 [34] A. Woytea, J. Nijsa, and R. Belmans, “Partial shadowing of photovoltaic arrays with different system configurations: literature review and field test results,” Solar Energy, vol. 74, p. 17, 2003. [35] F. Zhang, J. Maddy, G. Premier, and A. Guwy, “Novel current sensing photovoltaic maximum power point tracking based on sliding mode control strategy,” Solar Energy, vol. 118, p. 8086, 2015. [36] J. Zhaoa, X. Zhoub, Y. Mab, and W. Liub, “A novel maximum power point tracking stra- tegy based on optimal voltage control for photovoltaic systems under variable environmental conditions,” Solar Energy, vol. 122, p. 640649, 2015. Received on February 03, 2017 Revised on September 12, 2018
File đính kèm:
 simulation_of_reconfiguration_system_using_matlab_simulink_e.pdf
simulation_of_reconfiguration_system_using_matlab_simulink_e.pdf

