Quintic B-spline collocation method for numerical solution of the Generalized Benjamin-Bona-MahonyBurgers equation

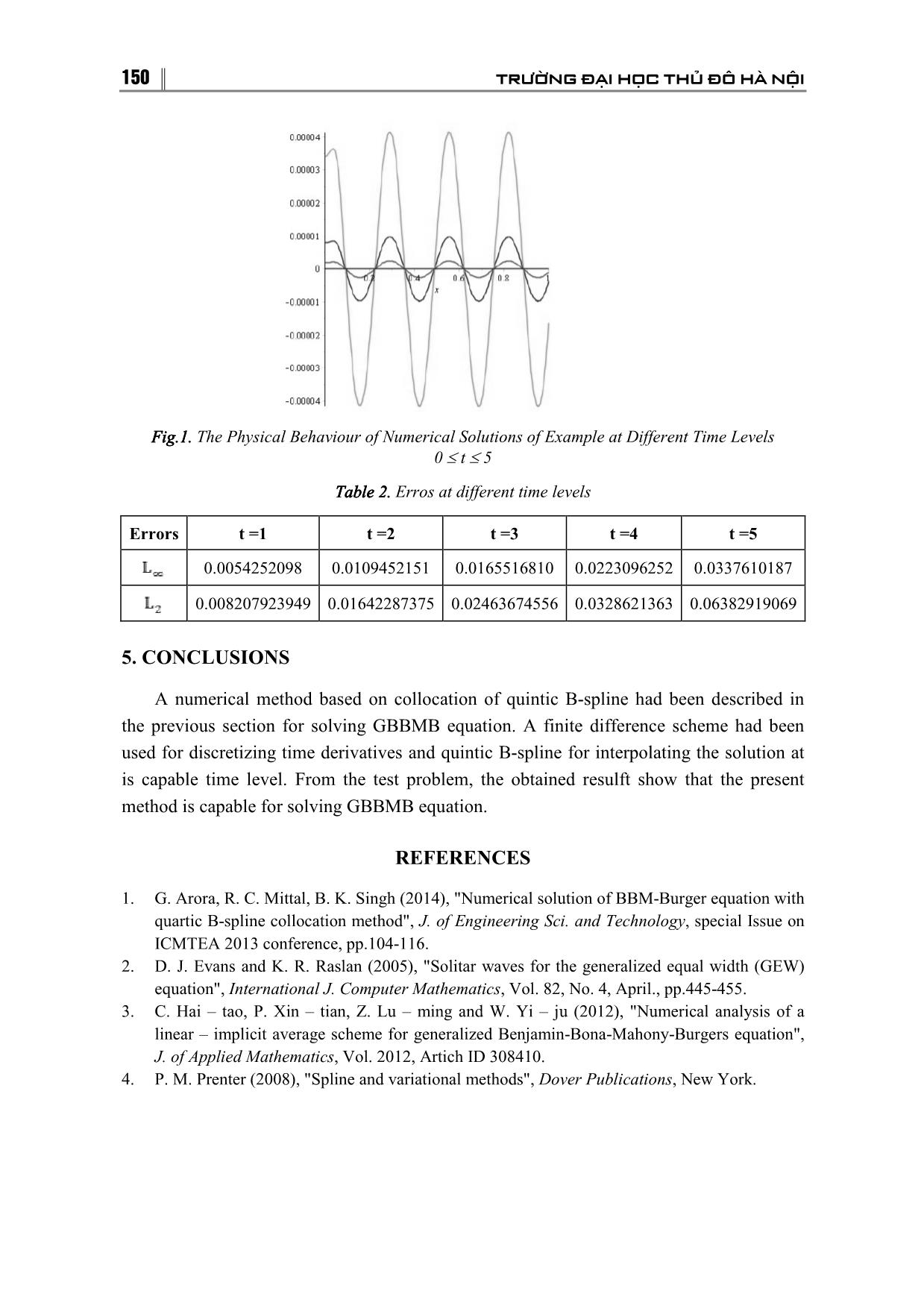
144 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
 QUINTIC BBSPLINESPLINE COLLOCATION METHOD FOR NUMERICAL 
 SOLUTION OF THE GENERALIZED BENJAMINBENJAMINBONABONABONAMAHONYMAHONYMAHONY
 BURGERS EQUATION 
 1( 1) 2 
 Nguyen Van Tuan , Nguyen Duc Thuyet
 1Hanoi Metropolitan University 
 2Vinh Phuc Vocational College 
 AAbbAbstractAb stractstract: In this paper, numerical solutions of the Generalized BenjaminBonaMahony
 Burgers (GBBMB) equation are obtained by collocation of quintic Bsplinesbased 
 method. Applying the VonNeumann stability analysis, the proposed method is shown to 
 be unconditionally stable. The numerical result shows that the present method is a 
 successful numerical technique for solving the GBBMB equation. 
 KeywordsKeywords: GBBMB equation; quintic Bspline; collocation method; finite difference. 
1. INTRODUCTION 
 In this paper we consider the solution of the GBBMB equation: 
 (1) 
 with the initial condition: 
 (2) 
and the boundary condition: 
 (3) 
where are constants, is an integer. 
 GBBMB equations play a dominant role in many branches of science and engineering. 
In the past several years, many different methods have been used to solution of the 
GBBMB equation and some their cases, see [1, 3, 5]. 
 The paper is used quintic Bspline collocation method for equation (1). 
(1) Nhn bài ngày 15.7.2016; gi phn bin và duyt ñăng ngày 15.9.2016 
 Liên h tác gi: Nguyn Văn Tun; Email: nvtuan@daihocthudo.edu.vn 
TẠP CHÍ KHOA HỌC −−− SỐ 8/2016 145 
2. QUINTIC B – SPLINE COLLOCATION METHOD 
 The interval is partitioned in to a mesh of uniform length by the 
knots such that: 
 Our numerical study for GBBMB equation using the collocation method with quintic 
 Bspline is to find an approximate solution to exact solution in the form: 
 (4) 
 are the quintic Bspline basis functions at knots, given by [4]. 
 The value of and its derivatives may be tabulated as in Table 1. 
 Table 1. and at the node points 
 x 
 0 1 26 66 26 1 0 
 0 0 0 
 0 0 
 Using the finite difference method, from the equation (1), we have: 
 (5) 
146 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
 The nolinear term in Eq. (5) can be approximated by using the following 
 formulas which obtainted by applying the Taylor expansion 
 So Eq. (5) can be rewritten as 
 (6) 
 Using the value given in Table 1, Eq. (6) can be calculated at the knots so 
that at Eq. (6) reduces to 
 (7) 
 Where: 
 At Eq. (7) 
becames 
 (8) 
 Where: 
TẠP CHÍ KHOA HỌC −−− SỐ 8/2016 147 
 The system (8) consists of equations in the knowns 
 To get a solution to this system, we need four additional constraints. These constraints 
 are obtained from the boundary conditions (3) and can be used to eliminate from the 
 system (8). Then, we get the matrix system equation: 
 (9) 
where the matrix are pentadiagonal matrices and is 
the dimensional colum vector. The algorithm is then used to solve the system (8). 
We apply first the intial condition: 
 (10) 
then we need that the approximately solution is satisfied folowing conditions: 
 (11) 
 Eliminating and from the system (11), we get: 
where is the pentadiagonal matrix given by: 
  54 60 6 0 0 0 ... 0 
  
 101 135 105
  1 0 0 ... 0 
  4 2 4 
  1 26 66 26 1 0 ... 0 
  
  ... ... ... 
 A =
  
  ... ... ... 
  0 ... 0 1 26 66 26 1 
  
 105 135 101
  0 ... 0 0 1 
  4 2 4 
  
  0 ... 0 0 0 6 60 54 
and 
148 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
3. STABILITY ANALYSIS 
 To apply the VonNeumann stability for the system (7), we must first linearize this 
 system. 
 We have: 
 (12) 
 where is the mode number and is the element size. 
 Being applicable to only linear schemes the nonlinear term is linearized by 
taking as a locallyconstant value The linearized form of proposed scheme is given as 
 (13) 
 Where: 
TẠP CHÍ KHOA HỌC −−− SỐ 8/2016 149 
 Substitretion of into Eq. (13) leads to: 
 (14) 
 Simplifying Eq. (14), we get 
 Where: 
 It is clear that 
 Therefore, the linearized numerical scheme for the GBBMB equation is 
 unconditionally stable. 
4. NUMERICAL EXAMPLE 
 We now obtain the numerical solution of the GBBMB equation for a problem. To 
show the efficiency of the present method for our problem in comparison with the exact 
solution, we report and using formula 
 where is numerical solution and denotes exact solution. 
 Example . Consider the GBBMB equation with . The exact of Eq. (1) 
is given in [7] 
 where and represent the amplitude and veloeity of a single solitary 
 wave initially centered at 
 We choose the following parameters 
 . 
150 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
 Fig.1. The Physical Behaviour of Numerical Solutions of Example at Different Time Levels 
 0 ≤ t ≤ 5 
 Table 2. Erros at different time levels 
 Errors t =1 t =2 t =3 t =4 t =5 
 0.0054252098 0.0109452151 0.0165516810 0.0223096252 0.0337610187 
 0.008207923949 0.01642287375 0.02463674556 0.0328621363 0.06382919069 
5. CONCLUSIONS 
 A numerical method based on collocation of quintic Bspline had been described in 
the previous section for solving GBBMB equation. A finite difference scheme had been 
used for discretizing time derivatives and quintic Bspline for interpolating the solution at 
is capable time level. From the test problem, the obtained resulft show that the present 
method is capable for solving GBBMB equation. 
 REFERENCES 
1. G. Arora, R. C. Mittal, B. K. Singh (2014), "Numerical solution of BBMBurger equation with 
 quartic Bspline collocation method", J. of Engineering Sci. and Technology , special Issue on 
 ICMTEA 2013 conference, pp.104116. 
 2. D. J. Evans and K. R. Raslan (2005), "Solitar waves for the generalized equal width (GEW) 
 equation", International J. Computer Mathematics , Vol. 82, No. 4, April., pp.445455. 
3. C. Hai – tao, P. Xin – tian, Z. Lu – ming and W. Yi – ju (2012), "Numerical analysis of a 
 linear – implicit average scheme for generalized BenjaminBonaMahonyBurgers equation", 
 J. of Applied Mathematics , Vol. 2012, Artich ID 308410. 
 4. P. M. Prenter (2008), "Spline and variational methods", Dover Publications , New York. 
TẠP CHÍ KHOA HỌC −−− SỐ 8/2016 151 
5. K. Shin – ichi and M. Ming and O. Seiro (2000), Convergence to diffusion waves of the 
 solutions for BenjaminBonaMahonyBurgers equations, Applicable Analysis, Vol. 75 (3 – 
 40), pp.317340. 
 6. SirajUlIslam, FazalIHad and Ikram A. Tirmizi (2010),"Collocation method using quartic 
 Bspline for numerical solution of the modified equal width wave equation", J. Appl. Math. 
 Informatics , Vol. 28, No.34, pp.611624. 
 7. G. Turabi, B. G. K. Seydi (2011), "Septic B – spline collocation Method for the numerical 
 solution of the modified equal width wave equation", Applied Mathematics , 2, pp.739749. 
 8. M. Zarebnia and R. Parvaz (2017), Numerical study of the BenjaminBonaMahonyBurgers 
 equation , Bol. Soc. Paran. Mat. Vol. 35 1, pp.127138. 
 PHƯƠNG PHÁP COLLOCATION VI CƠ S BSPLINE BC 5 
 GII PHƯƠNG TRÌNH GENERALIZED BENJAMINBONA
 MAHONYBURGERS 
 Tóm tttttt: Trong bài báo này chúng ta s dng phương pháp collocation vi cơ s B – 
 spline bc 5 gii xp x phương trình generalized Benjamin – Bona – mahony – Burgers. 
 S dng phương pháp Von – Neumann h phương trình sai phân n ñnh vô ñiu kin. 
 Kt qu s chng t phương pháp ñưa ra hu hiu ñ gii phương trình trên. 
 TTTT khoákhoá: Phương trình GBBMB, spline bc 5, phương pháp collocation, phương pháp sai 
 phân hu hn.