Nghiên cứu trường ứng suất của nòng đơn bằng phương pháp đẳng hình học

Nghiên cứu khoa học công nghệ 
 NGHIÊN CỨU TRƯỜNG ỨNG SUẤT CỦA NÒNG ĐƠN 
 BẰNG PHƯƠNG PHÁP ĐẲNG HÌNH HỌC 
 Nguyễn Văn Dũng*, Lê Xuân Long , Lê Xuân Trường 
 Tóm tắt: Phương pháp đẳng hình học (IGA) được xem là một trong những phương 
 pháp số được dùng phổ biến nhất hiện nay để giải các bài toán trong mô hình toán học và 
 kỹ thuật nhưng phương pháp này vẫn chưa được ứng dụng rộng rãi trong tính toán các hệ 
 thống vũ khí. Bài báo này trình bày ứng dụng của đẳng hình học để phân tích trường ứng 
 suất trong nòng đơn súng máy. Những kết quả tính toán thu được bằng phương pháp đẳng 
 hình học tiệm cận rất tốt về nghiệm giải tích là sự lý giải cho ứng dụng rộng rãi của nó. 
Từ khóa: Đẳng hình học; Áp suất khí thuốc; Nurbs; Phần tử hữu hạn. 
 1. ĐẶT VẤN ĐỀ 
 Hiện nay, người ta sử dụng hai phương pháp chính để giải bài toán trường ứng suất và biến 
dạng nòng dưới tác dụng của tải xung áp suất khí thuốc: Phương pháp giải tích và phương pháp 
phân tích phần tử hữu hạn (FEA). Mỗi phương pháp đều có ưu điểm và nhược điểm. Phương 
pháp phần tử hữu hạn có hạn chế là sự sai khác hình học khi tính toán so với mô hình gốc, do 
vậy, kết quả tính toán để đạt được độ chính xác thì phải tăng khối lượng tính toán. 
 Phương pháp phân tích đẳng hình học (IGA) còn mới nhưng hiện đã được sử dụng rộng rãi 
trong hầu hết các bài toán kỹ thuật. Bên cạnh ưu điểm nổi bật là tính chính xác, phương pháp 
IGA còn có thể giảm khối lượng tính toán rất nhiều lần so với phương pháp FEA. Do vậy, bài 
báo này đề xuất sử dụng phương pháp IGA vào bài toán trường ứng suất, biến dạng của nòng 
đơn, đối tượng khảo sát là nòng súng PKMS. Mô hình tính toán trong bài báo được xây dựng 
theo bài toán 2 chiều (bài toán phẳng), cụ thể là bài toán biến dạng phẳng. 
 2. XÂY DỰNG MÔ HÌNH VÀ PHƯƠNG PHÁP GIẢI TRONG IGA 
2.1. Xây dựng mô hình 
2.1.1. Mô hình vật lý 
 Mô hình vật lý của bài toán được thể hiện ở hình 1 (bỏ qua áp suất khí quyển tác dụng vào mặt 
ngoài nòng). Do tính chất đối xứng nên chỉ cần xét 1/4 mô hình cùng với các điều kiện biên đối 
xứng. 
 Hình 1. Mô hình vật lý của bài toán. 
2.1.2. Mô hình trong IGA 
 Để xây dựng mô hình mặt Nurbs 1/4 hình khuyên, trước tiên xây dựng đường cong Nurbs mô 
tả 1/4 đường tròn. 
 - Mô hình 1/4 đường tròn bán kính 1 đơn vị: 
 Sử dụng véc tơ knot: Ξ = {0, 0, 0, 1, 1, 1} và các điểm điều khiển P1(1, 0); 
Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 143 
 Cơ kỹ thuật & Cơ khí động lực 
 P2(1, 1), P3(0, 1), véc tơ trọng số:  [1 1/ 2 1]. 
 Khi đó, đường tròn được định nghĩa [1]: 
 Ni, pi()
 CP( ); n i 
  Ni, pi()
 i 1
 Trong đó, Ni,p – Các hàm cơ sở, định nghĩa truy hồi bắt đầu với p = 0: 
 1 if ii   1
 Ni,0  
 0 otherwise
 Và với p 1: 
  i ip 1 
 NNNi, p()()() i , p 1  i 1, p 1  
 i p  i  i p 11  i 
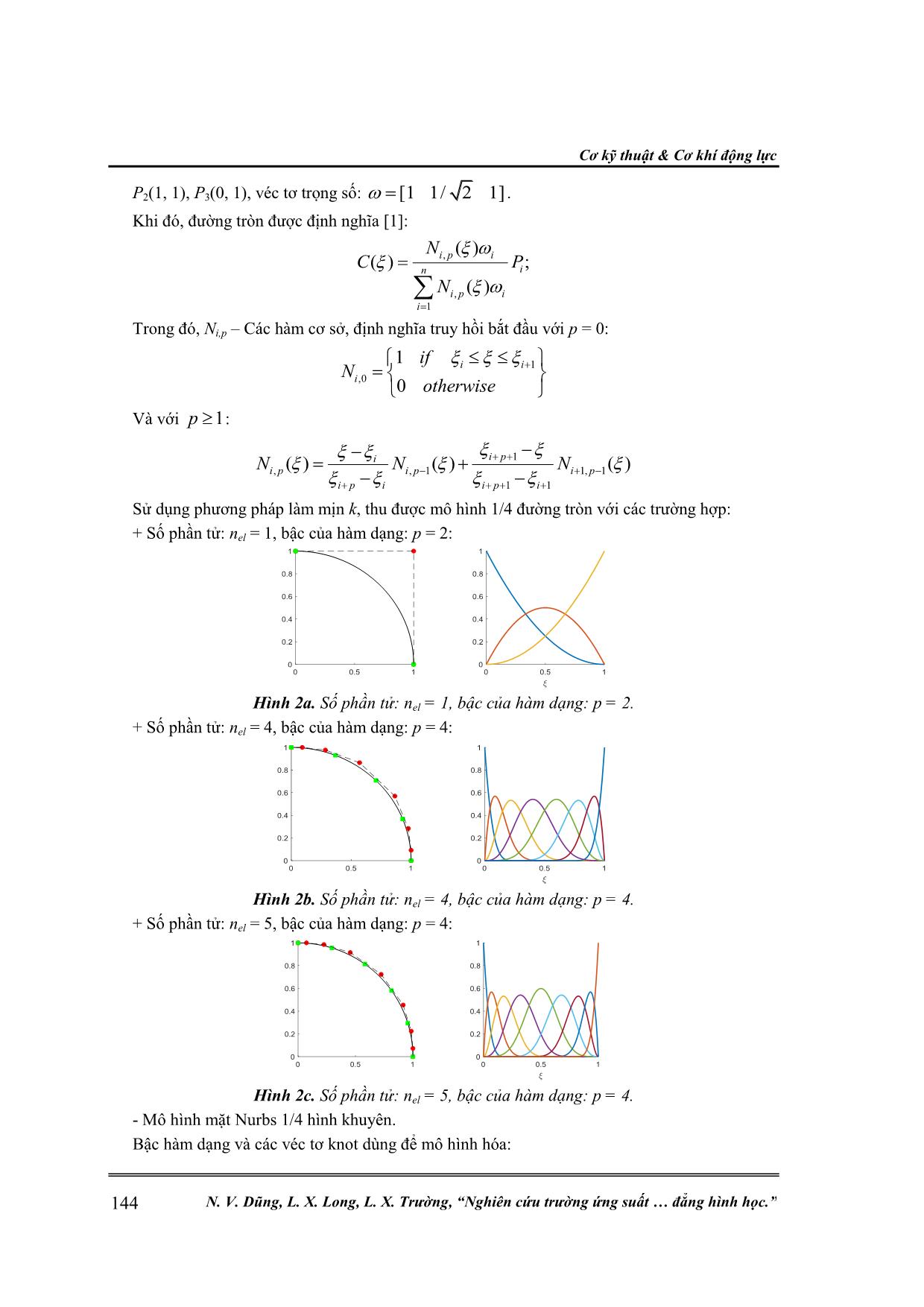
 Sử dụng phương pháp làm mịn k, thu được mô hình 1/4 đường tròn với các trường hợp: 
 + Số phần tử: nel = 1, bậc của hàm dạng: p = 2: 
 Hình 2a. Số phần tử: nel = 1, bậc của hàm dạng: p = 2. 
 + Số phần tử: nel = 4, bậc của hàm dạng: p = 4: 
 Hình 2b. Số phần tử: nel = 4, bậc của hàm dạng: p = 4. 
 + Số phần tử: nel = 5, bậc của hàm dạng: p = 4: 
 Hình 2c. Số phần tử: nel = 5, bậc của hàm dạng: p = 4. 
 - Mô hình mặt Nurbs 1/4 hình khuyên. 
 Bậc hàm dạng và các véc tơ knot dùng để mô hình hóa: 
144 N. V. Dũng, L. X. Long, L. X. Trường, “Nghiên cứu trường ứng suất  đẳng hình học.” 
Nghiên cứu khoa học công nghệ 
 Phương Bậc Véc tơ knot 
 ξ 2 Ξ = {0, 0, 0, 1, 1, 1} 
 η 1 Η = {0, 0, 1, 1} 
 Tọa độ các điểm điều khiển và trọng số: 
 j P1,j P2,j P3,j ω1,j ω2,j ω3,j 
 1 (rt , 0, 0) (rt , Rt, 0) (0, rt , 0) 1 1/√2 1 
 2 (rn , 0, 0) (rn , rt, 0) (0, rn , 0) 1 1/√2 1 
 Khi đó, mặt tròn được định nghĩa [1, 6]: 
 NM()()  
 pq, i,, p , j q i j 
 Rij, (,) nm
 NMi,, p()() , j q   i j
 ij 11
 Trong đó, Trong đó, Ni,p , Mj,q – Các hàm cơ sở. 
 Mô hình mặt Nurbs hình khuyên xây dựng trong IGA: 
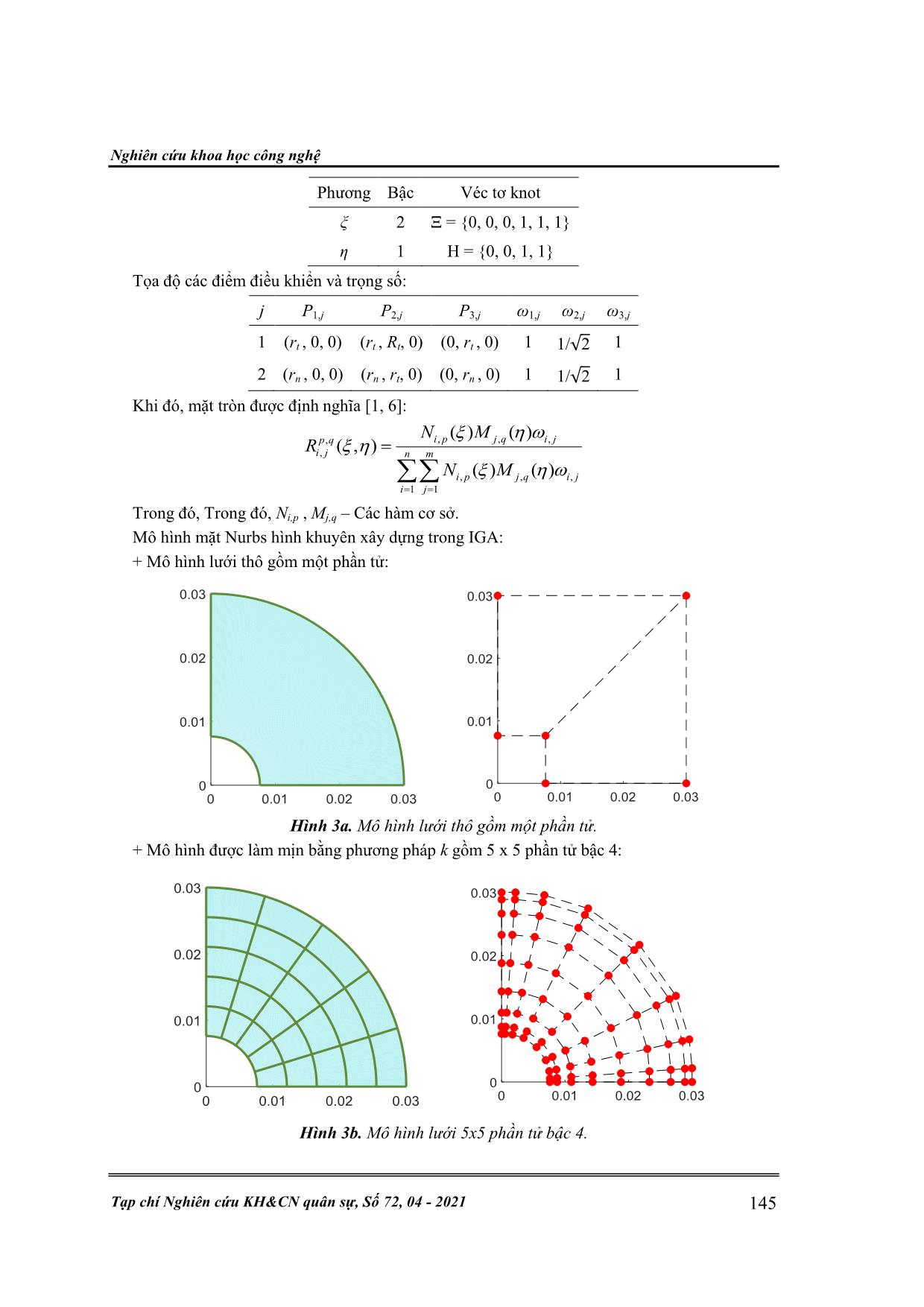
 + Mô hình lưới thô gồm một phần tử: 
 Hình 3a. Mô hình lưới thô gồm một phần tử. 
 + Mô hình được làm mịn bằng phương pháp k gồm 5 x 5 phần tử bậc 4: 
 Hình 3b. Mô hình lưới 5x5 phần tử bậc 4. 
Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 145 
 Cơ kỹ thuật & Cơ khí động lực 
2.2. Phương pháp giải trong IGA 
 Trong phân tích đẳng hình học, phương trình ma trận có dạng sau: 
 KdF 
 Trong đó, 
 T
 d - Ma trận chuyển vị: d u u... u u u ... u 
 x1 x 2 xnnp y 1 y 2 yn np
 K và F lần lượt là ma trận độ cứng và ma trận lực: 
 - Ma trận độ cứng: 
 K  BT DBd 
 e
 Trong đó, ma trận B được định nghĩa: 
 NN Nn
 12...en 0 0 ... 0
 x  x  x
 NN Nn 
 B 0 0 ... 012 ... en
 y  y  y
 NNNN NN  
 1 2...... nnenen 1 2
 y  y  y  x  x  x
 Với: 
 Ni – Hàm dạng [1]; 
 10 
 E 
 D 10
 1  1 2 
 12 
 00
 2
 E, ν: Modun đàn hồi và hệ số poisson của vật liệu. 
 - Ma trận lực: 
 F NTT f d  N P d  
 n
 e
 e t
 Trong đó, ma trận N được định nghĩa: 
 NNN12...n 0 0 0 0
 N en 
 0 0 0 0NNN ...
 12 nen
 3. KẾT QUẢ PHÂN TÍCH VÀ THẢO LUẬN 
 Sử dụng các kết quả mục 2, tác giả sẽ áp dụng phân tích đẳng hình học để giải bài toán ứng 
suất trên thành nòng đơn dưới tác dụng của áp suất khí thuốc. Sau đó, so sánh với nghiệm giải 
bằng phương pháp phần tử hữu hạn [2] và nghiệm giải tích [4] – nghiệm hiện được sử dụng rộng 
rãi, có độ chính xác cao. 
 Đối tượng khảo sát là nòng súng đại liên PKMS. 
 Các thông số đầu vào của bài toán được thể hiện ở bảng 1 [3]. 
146 N. V. Dũng, L. X. Long, L. X. Trường, “Nghiên cứu trường ứng suất  đẳng hình học.” 
Nghiên cứu khoa học công nghệ 
 Bảng 1. Thông số đầu vào bài toán phân tích ứng suất. 
 Thông số Ký hiệu Đơn vị Giá trị 
Mô đàn hồi của vật liệu nòng E N/m2 2.1010 
Hệ số poisson μ 0,3 
 6
Áp suất tại mặt cắt bên trong lòng nòng pt Pa 304.10 
Đường kính ngoài tại mặt cắt Dn m 0,03 
Đường kính trong tại mặt cắt Dt m 0,00762 
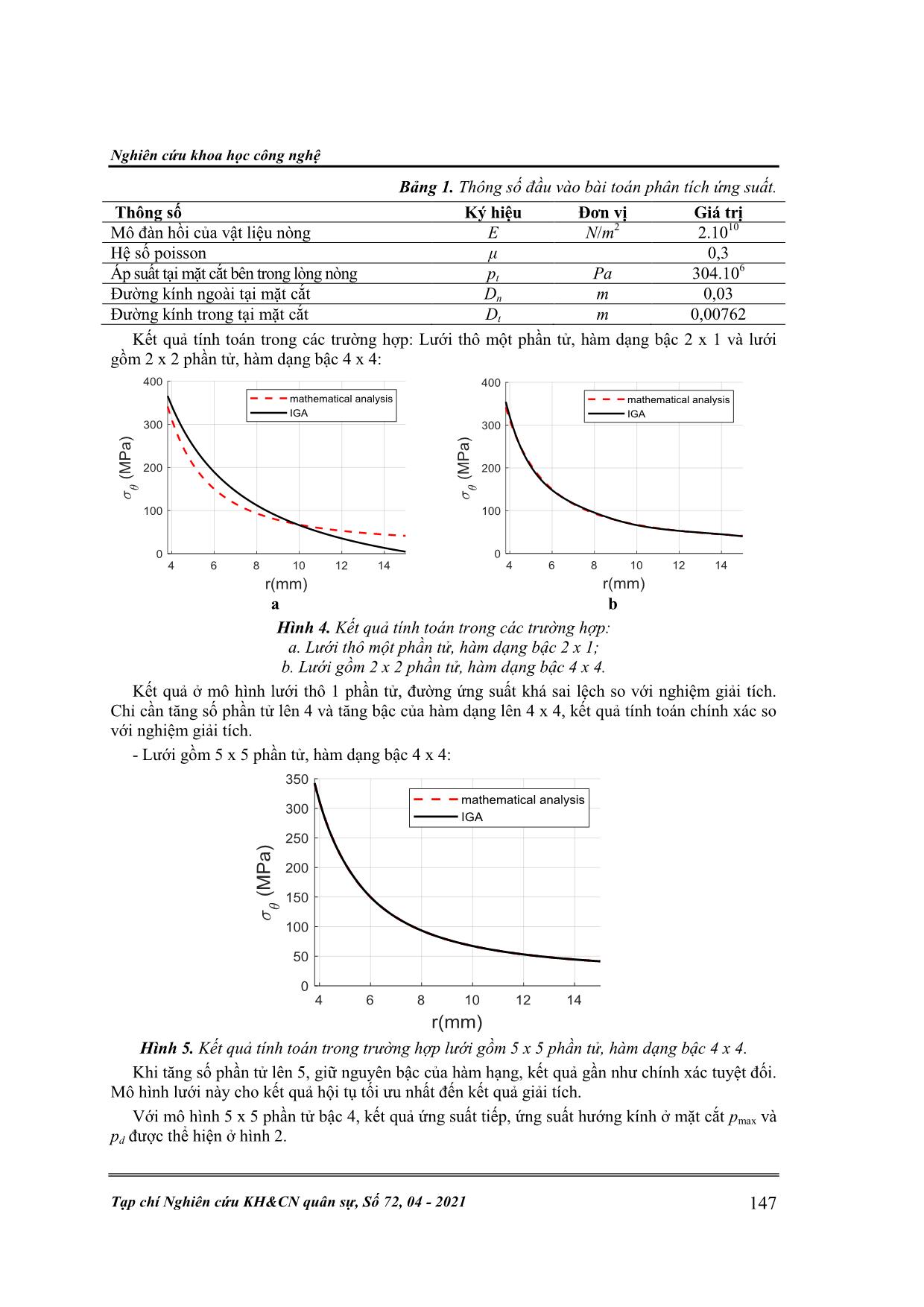
 Kết quả tính toán trong các trường hợp: Lưới thô một phần tử, hàm dạng bậc 2 x 1 và lưới 
gồm 2 x 2 phần tử, hàm dạng bậc 4 x 4: 
 a b 
 Hình 4. Kết quả tính toán trong các trường hợp: 
 a. Lưới thô một phần tử, hàm dạng bậc 2 x 1; 
 b. Lưới gồm 2 x 2 phần tử, hàm dạng bậc 4 x 4. 
 Kết quả ở mô hình lưới thô 1 phần tử, đường ứng suất khá sai lệch so với nghiệm giải tích. 
Chỉ cần tăng số phần tử lên 4 và tăng bậc của hàm dạng lên 4 x 4, kết quả tính toán chính xác so 
với nghiệm giải tích. 
 - Lưới gồm 5 x 5 phần tử, hàm dạng bậc 4 x 4: 
 Hình 5. Kết quả tính toán trong trường hợp lưới gồm 5 x 5 phần tử, hàm dạng bậc 4 x 4. 
 Khi tăng số phần tử lên 5, giữ nguyên bậc của hàm hạng, kết quả gần như chính xác tuyệt đối. 
Mô hình lưới này cho kết quả hội tụ tối ưu nhất đến kết quả giải tích. 
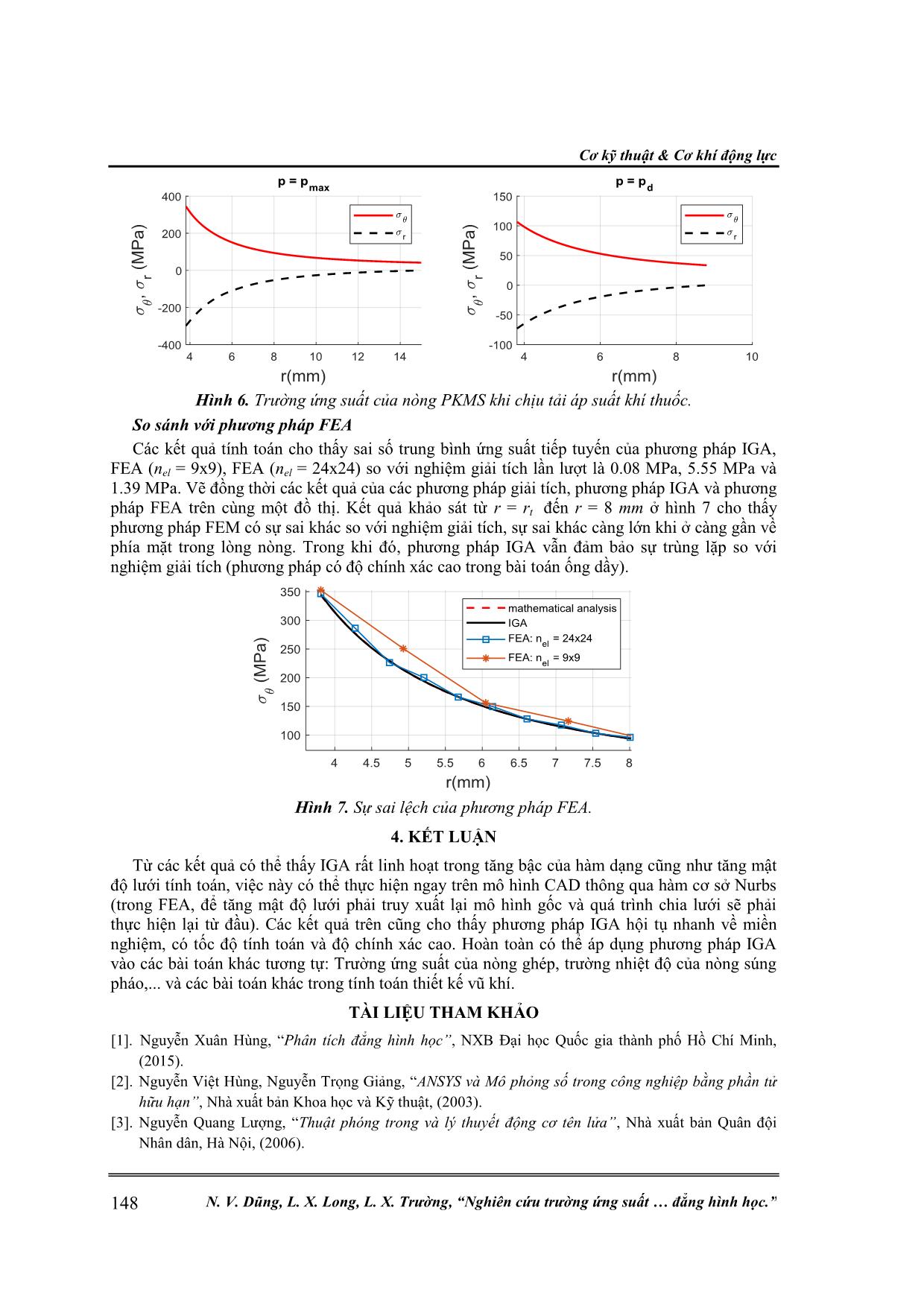
 Với mô hình 5 x 5 phần tử bậc 4, kết quả ứng suất tiếp, ứng suất hướng kính ở mặt cắt pmax và 
pd được thể hiện ở hình 2. 
Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 147 
 Cơ kỹ thuật & Cơ khí động lực 
 Hình 6. Trường ứng suất của nòng PKMS khi chịu tải áp suất khí thuốc. 
 So sánh với phương pháp FEA 
 Các kết quả tính toán cho thấy sai số trung bình ứng suất tiếp tuyến của phương pháp IGA, 
FEA (nel = 9x9), FEA (nel = 24x24) so với nghiệm giải tích lần lượt là 0.08 MPa, 5.55 MPa và 
1.39 MPa. Vẽ đồng thời các kết quả của các phương pháp giải tích, phương pháp IGA và phương 
pháp FEA trên cùng một đồ thị. Kết quả khảo sát từ r = rt đến r = 8 mm ở hình 7 cho thấy 
phương pháp FEM có sự sai khác so với nghiệm giải tích, sự sai khác càng lớn khi ở càng gần về 
phía mặt trong lòng nòng. Trong khi đó, phương pháp IGA vẫn đảm bảo sự trùng lặp so với 
nghiệm giải tích (phương pháp có độ chính xác cao trong bài toán ống dầy). 
 Hình 7. Sự sai lệch của phương pháp FEA. 
 4. KẾT LUẬN 
 Từ các kết quả có thể thấy IGA rất linh hoạt trong tăng bậc của hàm dạng cũng như tăng mật 
độ lưới tính toán, việc này có thể thực hiện ngay trên mô hình CAD thông qua hàm cơ sở Nurbs 
(trong FEA, để tăng mật độ lưới phải truy xuất lại mô hình gốc và quá trình chia lưới sẽ phải 
thực hiện lại từ đầu). Các kết quả trên cũng cho thấy phương pháp IGA hội tụ nhanh về miền 
nghiệm, có tốc độ tính toán và độ chính xác cao. Hoàn toàn có thể áp dụng phương pháp IGA 
vào các bài toán khác tương tự: Trường ứng suất của nòng ghép, trường nhiệt độ của nòng súng 
pháo,... và các bài toán khác trong tính toán thiết kế vũ khí. 
 TÀI LIỆU THAM KHẢO 
[1]. Nguyễn Xuân Hùng, “Phân tích đẳng hình học”, NXB Đại học Quốc gia thành phố Hồ Chí Minh, 
 (2015). 
[2]. Nguyễn Việt Hùng, Nguyễn Trọng Giảng, “ANSYS và Mô phỏng số trong công nghiệp bằng phần tử 
 hữu hạn”, Nhà xuất bản Khoa học và Kỹ thuật, (2003). 
[3]. Nguyễn Quang Lượng, “Thuật phóng trong và lý thuyết động cơ tên lửa”, Nhà xuất bản Quân đội 
 Nhân dân, Hà Nội, (2006). 
148 N. V. Dũng, L. X. Long, L. X. Trường, “Nghiên cứu trường ứng suất  đẳng hình học.” 
Nghiên cứu khoa học công nghệ 
[4]. Khổng Đình Tuy, Nguyễn Viết Trung, Nguyễn Văn Dũng , “Cơ sở thiết kế hệ thống pháo”, Nhà xuất bản 
 HVKTQS, (2009). 
[5]. H.Nguyen - Xuan, Chien H.Thai, T.Nguyen - Thoi, “Isogeometric finite element analysis of 
 composite sandwich plates using a higher order shear deformation theory”, Composites Part B: 
 Engineering, Volume 55, December 2013, Pages 558-574. 
 ABSTRACT 
 THE STUDY OF STRESS FIELD OF SINGLE GUN BARREL 
 USING ISOGEOMETRIC FINITE ELEMENT ANALYSIS 
 The isogeometric finite element method (IGA) is considered to be one of the most 
 popular numerical methods which are used for solving problems of engineering and 
 mathematical models. However, this method is still not widely used in weapon systems 
 engineering. This paper presents an application of isogeometric finite element analysis for 
 the examination of the stress field of a machine gun single barrel. The calculated results 
 obtained via the IGA approach show very good agreement with the analytical solution, 
 which makes it very useful for various applications. 
Keywords: Isogeometric analysis; Gas pressure; Nurbs; Finite elemets. 
 Nhận bài ngày 12 tháng 6 năm 2020 
 Hoàn thiện ngày 30 tháng 12 năm 2020 
 Chấp nhận đăng ngày 12 tháng 4 năm 2021 
Địa chỉ: Khoa Vũ khí/Học viện Kỹ thuật quân sự. 
 *Email: nguyenvandung.cl@gmail.com. 
Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 149