Multicast routing heuristic algorithms in non-splitting WDM networks

very 
node (except the multicast source1) used in any light-structure should have a degree bounded 
by two. It is called the degree constraint. 
3. Exact solutions 
Conventionally, the minimum cost multicast route corresponds to tree structure, since there 
is no redundant edge (arc) created. In non-splitting case, to guarantee this degree constraint, the 
solution should become a spider-like structure (a spider is a tree with at most one branch vertex 
[7]). Thus the solution for multicasting without splitters is conventionally a set of light-spiders. 
However, optical cross-connects allow light signals to be switched using input/output port pairs 
using a same wavelength as long as no collision occurs. In other words, nodes can be traversed 
more than once by a route using a wavelength. This makes it possible to realize non-elementary 
routes, as illustrated in Figure 2. Accordingly, three solutions for the request r=(s,{d1,d2}) on the 
same network condition are possible. Assume that every link is undirected and has unity cost 
(cost=1). Among possible solutions, light-spider (Fig. 2a) is an elementary route; whereas a set of 
light-paths (Fig. 2b) and a light-trail (Fig. 2c) which are examples of non-elementary routes. 
Obviously, in this context, non-elementary routes are preferred for the cost optimal solution than 
that of elementary one (light-spider). In the remainder of the paper, we call the mentioned non-
elementary routes light-spider hierarchy, to distinguish them from elementary light-spider. With 
this in mind, Theorem 1 gives exact solutions for MCM problem. 
Figure 2. Different solutions for the multicast request r=(s,{d1,d2}) 
Theorem 1. The exact solutions for MCM problem is a set of light-spider-hierarchies. 
In the next two sections, two heuristic algorithms to compute the approximate solutions 
for the MCM problem are presented and evaluated. 
1 Because optical networking allows nodes to be equipped with multiple transmitters, so the multicast source can 
inject the same wavelength to arbitrary number of successors. 
Hong Duc University Journal of Science, E.3, Vol.8, P (50 - 58), 2017 
53 
4. Heuristic algorithms 
In this section, we propose two efficient heuristic algorithms for MCM problem. 
4.1. Notations 
The two proposed heuristic algorithms work on layered graph model [8] instead of 
topology graph. To support the description of the two heuristic algorithms, we define some 
used notations as follows. 
G'=(V',A'): the layered graph constructed from the topology graph G=(V,A). 
r'=(s',D'): the corresponding request of the original request r=(s,D) created in the 
layered graph. We call s' the source, and d' D’s ink in short. 
MC_SET: the set of copies of the original source s in all the layers. 
CONN_SET: the set of connectors, which can be used to grow the current hierarchy H. 
For the aforementioned degree constraint, not all the vertices in H but a subset of them can be 
used to grow the hierarchy. They include the s', copies of the original source s, MC_SET and 
leaf-nodes in H. 
SPT(c,D'): the shortest path tree from source c to set D'. 
P(u,v): the shortest path from u to v. 
pred(d'): the predecessor of sink d' D' in the shortest path from s' to a sink d'. 
4.2. Nearest Destination First Algorithm 
Nearest Destination First (NDF) algorithm employs the basic idea of the Minimum Path 
Heuristic [6], which constructs an approximate Steiner tree from an initial vertex by iteratively 
adding a destination together with the shortest path (one at a time) until all the destinations 
reached. However, to satisfy the aforementioned degree constraint, MPH is modified in NDF 
heuristic to compute a valid route. 
Given a WDM network modeled by a topology graph G=(V,A), and a multicast request 
r=(s,D), NDF computes a minimum cost route for the corresponding request r'=(s',D') on 
layered graph G'=(V',A'). The algorithm returns a multicast route (hierarchy) H rooted at the 
source s' and spans the sinks D' = {d'1,d'2,.., d'D}. After pruning pseudo vertices and arcs from 
H, the resulting hierarchy H consists of a set of light-spider-hierarchies (LSHs). Each of these 
LSHs is located in a different layer, using a distinct wavelength. The description of NDF is 
given in the Algorithm 1. 
Initially, H consists of only the source s'. At each iteration, the algorithm searches for 
the nearest sink d' (line 11) from CONN_SET in the current hierarchy H to all the unreached 
sinks d' D'. This is done by gathering set CONN_SET as a virtual source c, and then creating 
a shortest path tree from c to the sinks in D' (line 7). Then the algorithm adds all vertices and 
arcs in the path P(c, pred(d')) to H, then removes the arcs in the path P(c,d') from the layered 
graph G', and update CONN_SET (lines 15-18). The algorithm terminates when there is no 
reachable destination remaining, or equivalently, H cannot be extended. To obtain the final 
multicast route, the final step prunes all the pseudo vertices (source and sinks) and the relevant 
pseudo arcs. The result is a set of LSHs routed at the source duplicates. Obviously, the 
Hong Duc University Journal of Science, E.3, Vol.8, P (50 - 58), 2017 
54 
resulting hierarchy respects all the aforementioned constraint. One example to illustrate the 
algorithm is shown in Figure 4. 
4.3. Critical Destination First Algorithm 
NDF algorithm always chooses the nearest sink to extend the current hierarchy. 
However, there are cases in which this policy is not effective. Let us see Fig.4 for an 
example. The network is shown in Figure 4a, with the request r=(s, {d1, d2, d3}. The 
corresponding layered graph with attached link costs are shown in Figure 4b. According to 
NDF, the first sink should be d'3 with the shortest path computed in layer 1: 
(s',s1,21,41,51,d13,d'3) with length (cost) of 4. For the next iteration, only d'1 can be reached 
(through layer 2) with the corresponding shortest path (s',s2,12,42,62,d21,d'1) with length of 8. 
The algorithm terminates and d'2 is not routed (Fig.4c)!. 
Now we see that d'2 has a least number of incoming arcs (1 in this case). Naturally, it 
should be chosen first since it has the least probability to be routed. Suppose that we choose 
d'2 first, the corresponding shortest path is (s', s1, 21, 41, 51, d12, d'2) with the length of 5 is 
added to the hierarchy. To choose the next sink between d'1 and d'3, since they have the same 
number of incoming links, the nearest one from the current hierarchy should be chosen. 
So the next sink should be d'3, and the corresponding shortest path (d12,51,d13,d'3) with 
the length of 3. Finally, the last sink d'1and the shortest path (s', s2, 12, 42, 62, d21, d'1) with the 
length of 8 is added to the hierarchy, resulting in the solution that reaches all the sinks with 
total cost of 16 as shown in Figure 4d. 
Hong Duc University Journal of Science, E.3, Vol.8, P (50 - 58), 2017 
55 
From the above observation, it is more beneficial to give higher priority to the sinks 
with lower incoming degree when extending the current hierarchy. We call these sinks critical 
destinations, and the incoming degree critical degree, since the incoming degree of a sink 
indicates the reachability of it from the source s' (Fig.4b). The least critical degree sink is thus 
the most critical destination. This gives rise to the new policy, i.e., choosing the most critical 
destination first, and hence the name: Critical Destination First (CDF) heuristic. When there 
are multiple sinks having the same critical degree, the nearest one from the current hierarchy 
will be chosen first as in NDF. 
Basically, CDF has the same framework as NDF, except that instead of finding a 
nearest sink of D', CDF finds the most critical sink from D'. This difference leads to two 
other different points in the description of CDF algorithm. The first point comes from the 
possibility that the shortest path P(c,pred(d')) may contain destination duplicates which are 
associated with some sinks. If so, the corresponding sinks must be removed from D'. The 
second different point is that the algorithm should update the reachability of all the affected 
sinks whenever P(c,pred(d')) has been added. These points are dealt using efficient technique in 
implementation in such a way that the complexity of CDF is the same order as NDF. For space 
limit, however, the description of CDF and all technical details are omitted in this paper. 
(a) A network and request r = (s,{d1,d2,d3}) (b) Layered graph 
(c) NDF solution: is blocked! (d) CDF solution: all destinations are routed! 
Figure 4. Illustration of the two heuristics 
Hong Duc University Journal of Science, E.3, Vol.8, P (50 - 58), 2017 
56 
5. Performance evaluation 
5.1. Performance metrics 
This work considers the case with arbitrary distribution of the wavelengths in the links. 
Hence, in the cases with limited available wavelengths, it is possible that not all the 
destinations routed for a given multicast request. Two blocking models are taken into account: 
full destination blocking and partial destination blocking [9]. Accordingly, under full 
destination blocking model, a multicast request is established if the source can reach to all the 
destinations. In this case, the appropriate metric to evaluate the solutions is the request 
blocking probability (RBP), i.e., the ratio of the number of requests blocked to the total 
number of requests arrived. For full destination blocking model, the destination blocking 
probability (DBP), i.e., the ratio between the destinations blocked and the total number of 
destinations of the request is calculated. 
5.2. Simulation settings 
The simulations are run on random network topologies G= (V,A), with random distribution 
of wavelengths in each arc. |V| is chosen in (50,100,150), W = 10, and |D| varies in (10%, 20%; 
, 90%) of |V|. For each |D|, we run 1000 instances, then calculate the 95% confident intervals for 
all the mean values of the above-defined blocking probability metrics (DBP and RBP). 
5.3. Results and discussion 
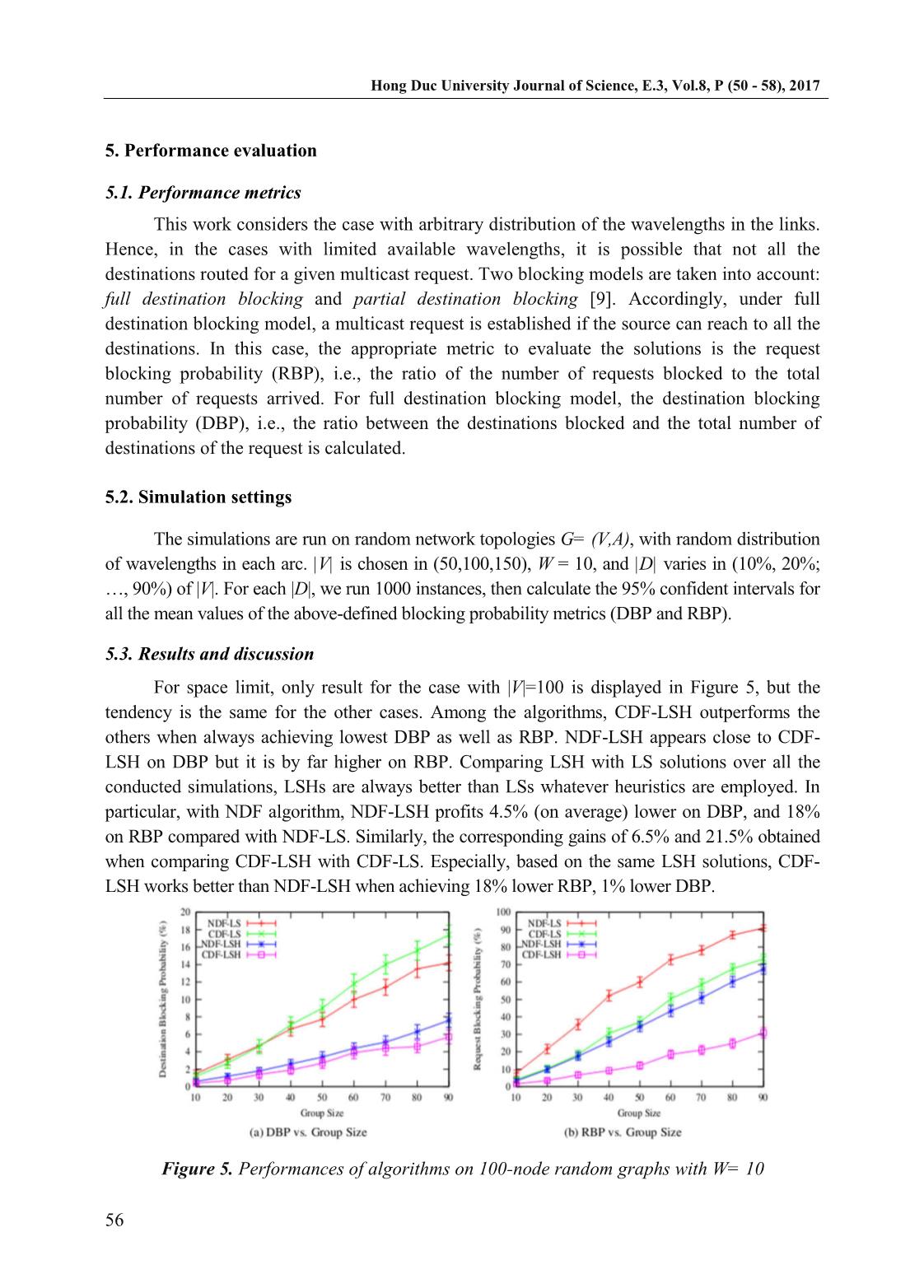
For space limit, only result for the case with |V|=100 is displayed in Figure 5, but the 
tendency is the same for the other cases. Among the algorithms, CDF-LSH outperforms the 
others when always achieving lowest DBP as well as RBP. NDF-LSH appears close to CDF-
LSH on DBP but it is by far higher on RBP. Comparing LSH with LS solutions over all the 
conducted simulations, LSHs are always better than LSs whatever heuristics are employed. In 
particular, with NDF algorithm, NDF-LSH profits 4.5% (on average) lower on DBP, and 18% 
on RBP compared with NDF-LS. Similarly, the corresponding gains of 6.5% and 21.5% obtained 
when comparing CDF-LSH with CDF-LS. Especially, based on the same LSH solutions, CDF-
LSH works better than NDF-LSH when achieving 18% lower RBP, 1% lower DBP. 
Figure 5. Performances of algorithms on 100-node random graphs with W= 10 
Hong Duc University Journal of Science, E.3, Vol.8, P (50 - 58), 2017 
57 
In short, the LSH solutions are always better than LS counterparts; and the CDF 
algorithm outperforms NDF. The results are expected and explainable. On one hand, by 
permitting vertices to be visited more than once, LSH allows to make full use of all the 
available wavelengths in the links while respecting the three aforementioned constraints. 
Consequently, more destinations can be reached with a limited available links and 
wavelengths, it in turn results in better blocking probability. On the other hand, CDF gives 
high priority to the most critical destinations to extend the hierarchy. Naturally, the most 
critical destinations will not be abandoned whenever there is a chance. Meanwhile NDF 
always chooses the nearest one, which may leave some destinations unreached even if there 
are many other choices. 
6. Conclusion 
The paper proposed two cost-effective heuristics for the MCM problem: Nearest 
Destination First and Critical Destination First. These algorithms aim at minimizing the total 
cost for a given multicast request under the arbitrary availability of wavelengths in non-
splitting networks. The two algorithms are designed to compute minimum-cost light-spider 
hierarchies based on the auxiliary layered graph model. They are different in the way of 
choosing the candidate destinations. NDF always chooses the nearest destinations at each 
iteration, while CDF selects the critical destinations first. The performances of the two 
heuristics are compared with each other. They show that, taking the critical degree of the 
destinations into account, particularly choosing the most critical destination to route first, 
results in a better solution under arbitrary wavelength configuration. Once again, the 
simulation results confirm that light-spider-hierarchies outperform light-spiders counterpart in 
supporting multicast in non-splitting networks. 
References 
[1] M. Ali and J. S. Deogun (2000), Power-efficient design of multicast wavelength-routed 
networks, Selected Areas in Communications, IEEE Journal on, vol. 18, no. 10, pp. 
1852 -1862. 
[2] M. Ali and J. S. Deogun (2000), Cost-effective implementation of multicasting in 
wavelength-routed networks, EEE/OSA Journal of Lightwave Technology, vol. 18, pp. 
1628 -1638. 
[3] R. Libeskind-Hadas (2000), Efficient collective communication in WDM networks with 
a power budget, in Computer Communications and Networks, 2000. Proceedings. 9th 
International Conference on, pp. 612 -616. 
[4] S. Yan and J. Deogun (2003), Multi-drop path model for multicast routing and 
wavelength assignment, Information Sciences, vol. 149, no. 1, pp. 113 -134. 
[5] D.-R. Din (2009), Heuristic Algorithms for Finding Light-Forest of Multicast Routing 
on WDM Network, Information Science and Engineering, vol. 25, pp. 83 -103. 
Hong Duc University Journal of Science, E.3, Vol.8, P (50 - 58), 2017 
58 
[6] H. Takahashi and A. Matsuyama (1980), An approximate solution for the Steiner 
problem in graphs, Mathematica Japonica, vol. 24, pp. 573 -577. 
[7] L. Gargano, P. Hell, L. Stacho, and U. Vaccaro (2002), Spanning trees with bounded 
number of branch vertices, in Automata, Languages and Programming, pp. 355 -365, 
Springer. 
[8] C. Chen and S. Banerjee (1996), A new model for optimal routing and wavelength 
assignment in wavelength division multiplexed optical networks, in INFOCOM ’96. 
Fifteenth Annual Joint Conference of the IEEE Computer Societies. Networking the 
Next Generation. Proceedings IEEE, vol. 1, pp. 164 -171, March 1996. 
[9] Dinh Danh Le, Fen Zhou, and Miklos Molnar (2015), Minimizing Blocking Probability 
for MCRWA problem in WDM Networks: Exact Solutions and Heuristic Algorithms, 
Journal of Optical Communications and Networking (JOCN). Vol. 7, Iss. 1, pp. 36-48.