Mô hình ngẫu nhiên đánh giá hiệu quả dự án tiết kiệm năng lượng

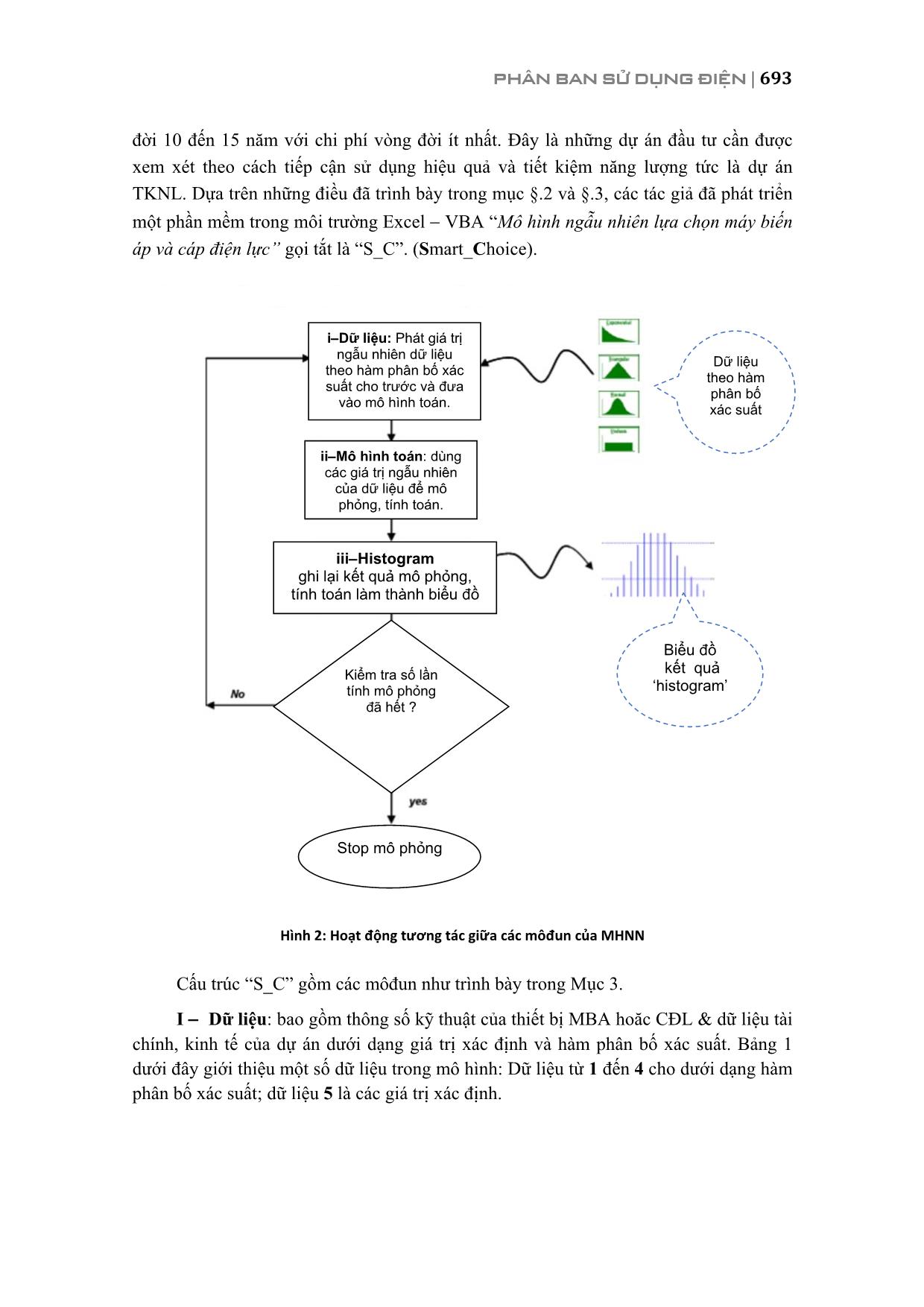
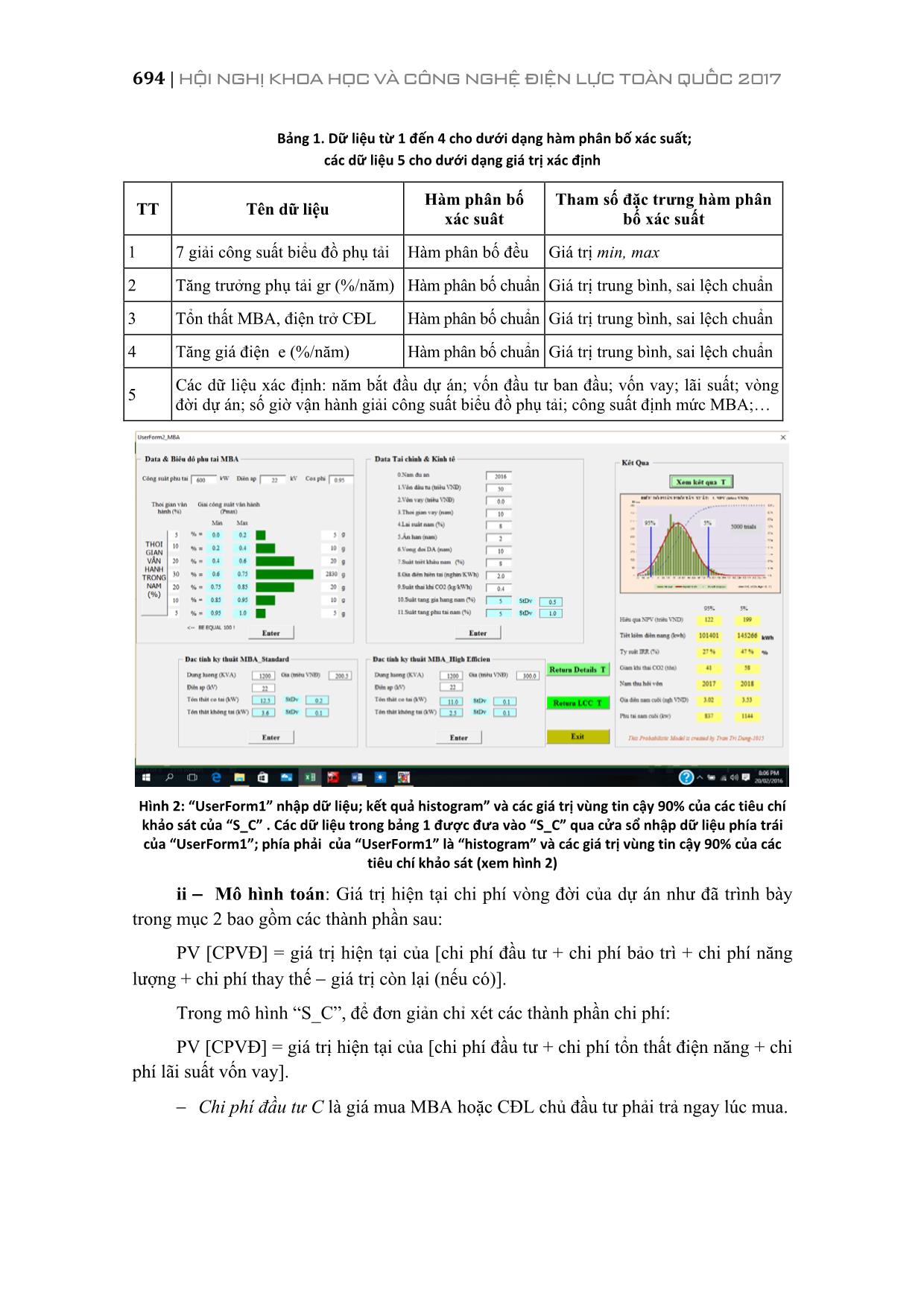
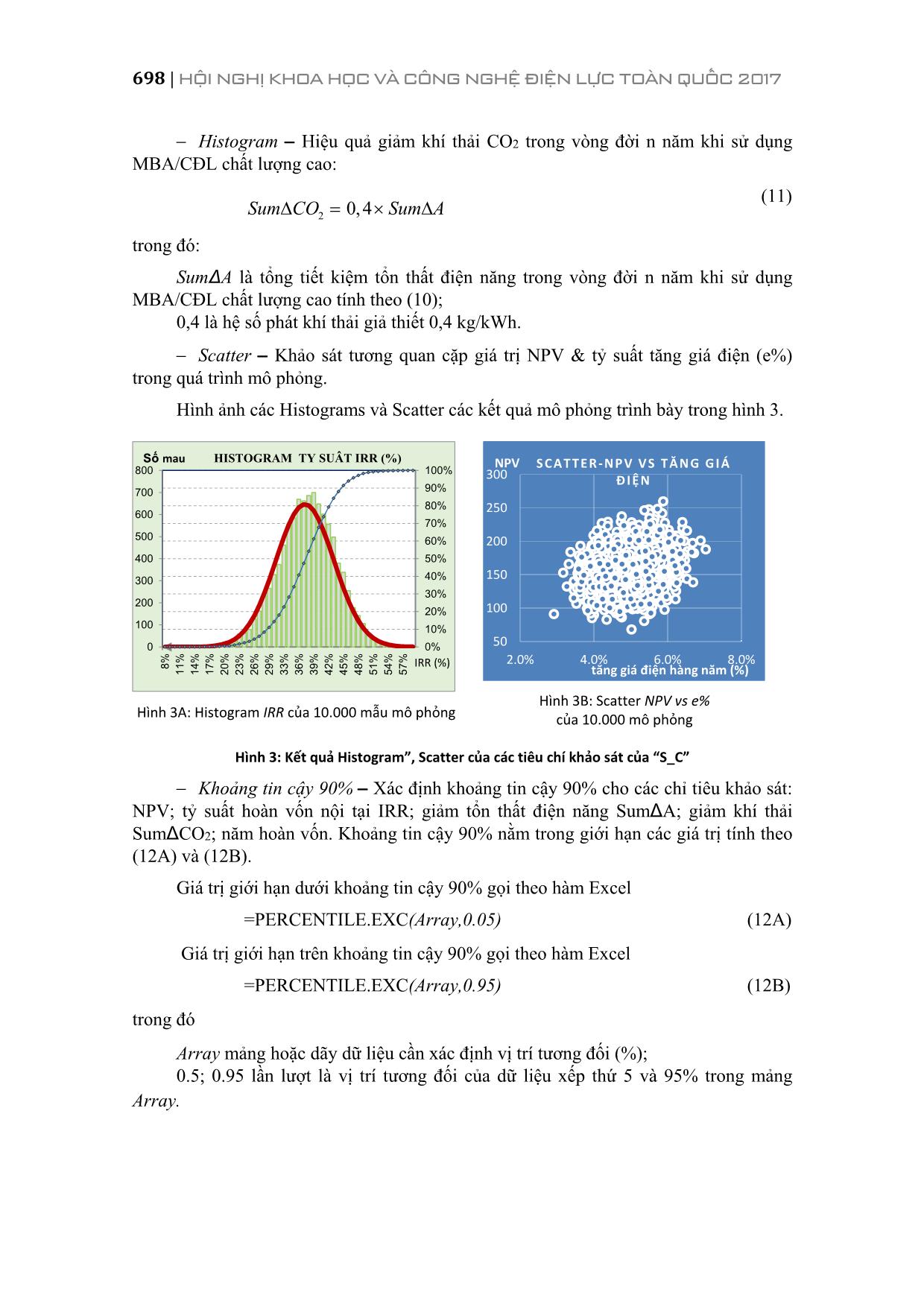
với dự án TKNL, phương án tốt nhất là phương án có giá trị 
hiện tại CPVĐ nhỏ nhất. 
3. PHÂN TÍCH CHI PHÍ VÒNG ĐỜI THEO “MÔ HÌNH NGẪU NHIÊN” 
Mô hình ngẫu nhiên (MHNN) dùng để xử lý các bài toán khi các dữ liệu đầu vào 
(Input Data) là bất định hoặc không chắc chắn (uncertainty). Trong thực tế, giá trị của 
mỗi dữ liệu thay đổi theo thời gian với quy luật riêng của nó. Mô hình cần phản ánh 
những biến động này và bảo đảm rằng kết quả đầu ra là tổ hợp ngẫu nhiên các kết quả 
biến động dữ liệu. Mô hình hoạt động theo cách mô phỏng hàng chục nghìn lần (mô 
phỏng Monte Carlo) các khả năng tổ hợp các giá trị ngẫu nhiên của các dữ liệu. Một 
mô hình như thế gọi là mô hình ngẫu nhiên. Ở mô hình này, khi hoạt động, các dữ liệu 
phát giá trị ngẫu nhiên theo hàm phân bố xác suất cho trước, mô hình tính toán và lưu 
trữ lại kết quả sau đó sắp xếp kết quả lại dưới dạng biểu đồ phân bố xác suất 
“histogram”. Số lần mô phỏng (số lần phát ngẫu nhiên giá trị dữ liệu) càng lớn thì biểu 
đồ “histogram” càng phong phú, gần hiện thực. Từ biểu đồ phân phối “histogram” có 
thể đánh giá khoảng tin cậy, giá trị min, max, của các kết quả biểu đồ y1, y2 như trên 
hình 1B. 
Trong mô hình xác lập (deterministic model) hình 1A, các dữ liệu vào là các giá 
trị xác định, x1, x2, x3, các kết quả ra là các giá trị xác định y1, y2, y3,.; Trong mô hình 
ngẫu nhiên hình 1B (stochastic model), một phần hoặc toàn bộ dữ liệu đầu vào thay vì 
là các giá trị xác định, sẽ được cho dưới dạng các tham số đặc trưng của hàm phân bố 
xác suất phù hợp của mỗi dữ liệu vào , x1, x2, x3, 
Cũng như mô hình xác lập, bước đầu tiên của MHNN là xây dựng mô hình tính 
toán với những công thức, điều kiên logic, điều kiện ràng buộc, mối quan hệ giữa biến 
độc lập, biến phụ thuộc để mô phỏng được bản chất thực của bài toán. 
692 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Hình 1A. Mô hình xác: lập các dữ liệu vào là 
các giá trị xác định, x1, x2, x3, các kết quả ra 
là các giá trị xác định y1, y2, y3 
Hình 1B. Mô hình ngẫu nhiên; dữ liệu đầu vào dưới 
dạng các tham số đặc trưng của hàm phân bố xác suất 
phù hợp của mỗi dứ liệu vào , x1, x2, x3, kết quả đầu 
ra dưới dạng biểu đồ phân bố xác suất ‘histogram’. 
Hình 1Input & Output của mô hình xác lập và mô hình ngẫu nhiên 
Cấu trúc của MHNN gồm các môđun chính (i) Dữ liệu: Phát hay tạo ra các giá trị 
ngẫu nhiên dữ liệu theo quy luật hàm phân bố xác suất cho trước; (ii) Mô hình toán: các 
công thức, điều kiện ràng buộc, mối quan hệ giữa biến độc lập, biến phụ thuộc mô tả 
đúng đắn bản chất các vấn đề cần cần khảo sát, tính toán của bài toán; (iii) Histogram: 
lưu trữ lại kết quả mô phỏng tính toán, sắp xếp kết quả dưới dạng biểu đồ phân bố xác 
suất “histogram”, “scatter” (xin xem hình 2). 
Hoạt động tương tác giữa các môđun của MHNN trình bày trên hình 2. Với cấu 
trúc như vậy, người kỹ sư có thể thực hiện số lần mô phỏng các khả năng tổ hợp các giá 
trị ngẫu nhiên của các dữ liệu lớn bao nhiêu tuỳ ý để có biểu đồ “histogram”, “scatter” 
kết quả đáng tin cậy thể hiện bản chất vấn đề khảo sát, nghiên cứu. 
Như vậy, trong MHNN, môđun (ii) hoàn toàn tương tự như trong mô hình xác lập 
nhưng có thêm môđun (i) và (iii) hỗ trợ. Nói cách khác, MHNN là sự tính lặp nhiều lần 
mô hình xác lập với các tập tổ hợp giá trị dữ liệu ngẫu nhiên khác nhau. 
4. MÔ HÌNH NGẪU NHIÊN LỰA CHỌN MÁY BIẾN ÁP VÀ CÁP ĐIỆN LỰC THEO CPVĐ 
Các công ty điện lực thường phải thực hiện những dự án phát triển, mở rộng hoặc 
cải tạo lưới phân phối cung cấp điện cho khách hàng. Nội dung chủ yếu của các dự án 
này là lựa chọn máy biến áp (MBA) và dây cáp điện lực (CĐL) là những phần tử chủ 
yếu trong lưới phân phối điện sao cho đảm bảo yêu cầu kinh tế kỹ thuật trong vòng 
PHÂN BAN SỬ DỤNG ĐIỆN | 693 
đời 10 đến 15 năm với chi phí vòng đời ít nhất. Đây là những dự án đầu tư cần được 
xem xét theo cách tiếp cận sử dụng hiệu quả và tiết kiệm năng lượng tức là dự án 
TKNL. Dựa trên những điều đã trình bày trong mục §.2 và §.3, các tác giả đã phát triển 
một phần mềm trong môi trường Excel VBA “Mô hình ngẫu nhiên lựa chọn máy biến 
áp và cáp điện lực” gọi tắt là “S_C”. (Smart_Choice). 
Hình 2: Hoạt động tương tác giữa các môđun của MHNN 
Cấu trúc “S_C” gồm các môđun như trình bày trong Mục 3. 
I Dữ liệu: bao gồm thông số kỹ thuật của thiết bị MBA hoăc CĐL & dữ liệu tài 
chính, kinh tế của dự án dưới dạng giá trị xác định và hàm phân bố xác suất. Bảng 1 
dưới đây giới thiệu một số dữ liệu trong mô hình: Dữ liệu từ 1 đến 4 cho dưới dạng hàm 
phân bố xác suất; dữ liệu 5 là các giá trị xác định. 
i Dữ liệu: Phát giá trị 
ngẫu nhiên dữ liệu 
theo hàm phân bố xác 
suất cho trước và đưa 
vào mô hình toán. 
ii Mô hình toán: dùng 
các giá trị ngẫu nhiên 
của dữ liệu để mô 
phỏng, tính toán. 
iii Histogram 
ghi lại kết quả mô phỏng, 
tính toán làm thành biểu đồ 
Stop mô phỏng 
Dữ liệu 
theo hàm 
phân bố 
xác suất 
Biểu đồ 
 kết quả 
‘histogram’ 
Kiểm tra số lần 
tính mô phỏng 
đã hết ? 
694 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Bảng 1. Dữ liệu từ 1 đến 4 cho dưới dạng hàm phân bố xác suất; 
các dữ liệu 5 cho dưới dạng giá trị xác định 
TT Tên dữ liệu Hàm phân bố xác suât 
Tham số đặc trưng hàm phân 
bố xác suất 
1 7 giải công suất biểu đồ phụ tải Hàm phân bố đều Giá trị min, max 
2 Tăng trưởng phụ tải gr (%/năm) Hàm phân bố chuẩn Giá trị trung bình, sai lệch chuẩn 
3 Tổn thất MBA, điện trở CĐL Hàm phân bố chuẩn Giá trị trung bình, sai lệch chuẩn 
4 Tăng giá điện e (%/năm) Hàm phân bố chuẩn Giá trị trung bình, sai lệch chuẩn 
5 Các dữ liệu xác định: năm bắt đầu dự án; vốn đầu tư ban đầu; vốn vay; lãi suất; vòng đời dự án; số giờ vận hành giải công suất biểu đồ phụ tải; công suất định mức MBA; 
Hình 2: “UserForm1” nhập dữ liệu; kết quả histogram” và các giá trị vùng tin cậy 90% của các tiêu chí 
khảo sát của “S_C” . Các dữ liệu trong bảng 1 được đưa vào “S_C” qua cửa sổ nhập dữ liệu phía trái 
của “UserForm1”; phía phải của “UserForm1” là “histogram” và các giá trị vùng tin cậy 90% của các 
tiêu chí khảo sát (xem hình 2) 
ii Mô hình toán: Giá trị hiện tại chi phí vòng đời của dự án như đã trình bày 
trong mục 2 bao gồm các thành phần sau: 
PV [CPVĐ] = giá trị hiện tại của [chi phí đầu tư + chi phí bảo trì + chi phí năng 
lượng + chi phí thay thế giá trị còn lại (nếu có)]. 
Trong mô hình “S_C”, để đơn giản chỉ xét các thành phần chi phí: 
PV [CPVĐ] = giá trị hiện tại của [chi phí đầu tư + chi phí tổn thất điện năng + chi 
phí lãi suất vốn vay]. 
 Chi phí đầu tư C là giá mua MBA hoặc CĐL chủ đầu tư phải trả ngay lúc mua. 
PHÂN BAN SỬ DỤNG ĐIỆN | 695 
 Chi phí tổn thất điện năng là chi phí tính bằng tiền Đ do tổn thất điện năng khi 
vận hành MBA hoặc CĐL. 
Để tính được giá trị hiện tại tổng chi phí tổn thất điện năng vòng đời PV [CPVĐ] 
của MBA hoặc CĐL cần xác định tổn thất công suất ứng với mỗi mức phụ tải Si và thời 
gian ti ; i = 1, 2,., 7 theo biểu đồ phụ tải hàng năm cho trước. Biểu đồ này được chia 
thành 7 dải công suất Si mỗi dải có số giờ vận hành ti (tổng thời gian vận hành ∑ ti ≈ 
8760 giờ). Lưu ý rằng, theo dòng 1 bảng 1, dải công suất Si là dữ liệu ngẫu nhiên (biến 
ngẫu nhiên) theo phân bố đều giữa giá trị Simin và Simax; mặt khác Si tăng trưởng hàng 
năm trong vòng đời n năm với tốc độ gr (%/năm) theo phân bố chuẩn. Như vậy, phụ tải 
MBA hoặc CĐL tại giải công suất i, năm thứ j sẽ là: 
   jiiiji grSSRANDSS 1)(() minmaxmin (1) 
 Trong đó: 
j
iS là phụ tải MBA hoặc CĐL tại giải công suất i, năm thứ j; i = 1,,7; 
j = 1,, n; 
RAND ( ) là số thực có giá trị ngẫu nhiên trong khoảng [0,1] do hàm RAND ( ) 
trong Excel tạo ra; 
gr là suất tăng trưởng phụ tải hàng năm (%) có giá trị ngẫu nhiên gọi theo hàm 
chuẩn trong Excel tạo ra gr = NormInv(grtb,,grsl), trong đó tham số grtb là giá trị trung 
bình, grsl là sai lệch chuẩn của gr. 
Biểu thức tính tổn thất công suất MBA phụ thuộc vào phụ tải S, tổn thất không tải 
Po (kw) và tổn thất có tải Pk (kw) của máy biến áp. 
2
)( 
MBA
i
koii S
SPPSP (2) 
trong đó, SMBA là dung lượng định mức của MBA. 
Tương tự, tổn thất công suất CĐL phụ thuộc vào điện trở thuần Ro (Ω/km), điện 
áp vận hành U (kV), chiều dài L (km) và phụ phụ tải Si (kVA) của cáp. 
2
)( 
U
SRLSP ioii (3) 
Lưu ý rằng trong (2) và (3), các giá trị tổn thất không tải Po (kW); tổn thất có tải 
Pk (kW); Ro (Ω /km) có giá trị ngẫu nhiên gọi theo hàm chuẩn trong Excel tạo ra = NormInv(). 
Từ (2) và (3), dễ dàng xác định tổn thất điện năng năm thứ j trong vòng đời n năm 
j = 1,, n của dự án. 
 i
j
ii
i
j tSPA 
)(
7
1
 (4) 
696 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
trong đó: 
∆Aj: tổn thất điện năng năm thứ j trong vòng đời n năm của dự án; 
ti: thời gian mang tải (giờ) tương ứng với phụ tải Si; 
7 bảy (7) dải biểu đồ phụ tải MBA hoặc CĐL; 
j
iS : phụ tải MBA hoặc CĐL tại dải công suất i, năm thứ j; i = 1,, 7; j = 1,, n 
được tính theo biểu thức (1); 
)( jii SP : tổn thất công suất của MBA hoặc của CĐL khi mang phụ tải jiS được 
tính theo (2) hoặc (3). 
Từ (4) dễ dàng xác định chi phí (Đ) tổn thất điện năng năm thứ j trong vòng đời n 
năm; j = 1,, n của dự án Aj: 
 jjj AeGA )1(0 (5) 
trong đó: 
Aj: chi phí tổn thất điện năng năm thứ j trong vòng đời n năm của dự án; 
G0: giá điện hiện tại 103 Đ/kWh; 
e: suất tăng giá hàng năm (%) có giá trị ngẫu nhiên gọi theo hàm chuẩn trong 
Excel tạo ra e = NormInv(etb,,esl), trong đó tham số etb là giá trị trung bình, esl là sai lệch 
chuẩn của e; 
G0(1+e)j: giá điện năm thứ j 103 Đ/kWh; 
∆Aj: tổn thất điện năng năm thứ j trong vòng đời n năm của dự án tính theo (4). 
 Chi phí vốn vay: Chi phí vốn vay V (triệu Đ) là số tiền trả đều hàng năm bao 
gồm vốn + lãi trong khoảng thời gian cho vay. Chi phí này tính theo hàm Excel: 
 V = PMT(r,t, L,1) (6) 
với các tham số biến lần lượt là r lãi suất vay (%/năm); t thời gian vay (năm), L số tiền 
vay (triệu Đ) và 1/0 trả vào đầu/cuối năm. 
Cuối cùng, tương tự biểu thức (*), giá trị hiện tại tổng chi phí vòng đời dự án PV 
[VĐ] được tính theo (5): 
j
jn
j d
VACPV
)1(
)VD(
1 
 
 (7) 
trong đó: 
PV (VĐ): giá trị hiện tại tổng chi phí vòng đời n MBA hoặc CĐL; 
C: giá mua MBA hoặc CĐL; 
Aj: chi phí tổn thất điện năng năm thứ j trong vòng đời n năm của dự án; 
V: chi phí vốn vay hàng năm bao gồm vốn + lãi (nếu có); 
PHÂN BAN SỬ DỤNG ĐIỆN | 697 
d: suất chiết khấu (discount rate) để quy đổi dòng tiền về giá trị hiện tại; 
j: năm thứ j; j=1,2,n; 
n: số năm khảo sát hay vòng đời dự án. 
 Tổng chi phí vòng đời: Các biểu thức được (2), (3), (4) và (5) dùng để tính tổng 
chi phí vòng đời PV (VĐ) cho lựa chọn giữa MBA/CĐL tiêu chuẩn PVtc (VĐ) và 
MBA/CĐL chất lượng cao – PVcl (VĐ). 
So sánh giữa PVtc (VĐ) và PVcl (VĐ) để đưa ra quyết định chính là nguyên tắc sử 
dụng hiệu quả & tiết kiệm năng lượng theo tổng chi phí vòng đời. 
iii Kết quả mô hình Histograms Scatter: 
Mô hình đã khảo sát, phân tích các tiêu chí, trình bày các kết quả dưới dạng biểu 
đồ histogram, scatter và giá trị khoảng tin cậy 90%. Những tiêu chí khảo sát là: 
 Histogram NPV Giá trị hiện tại hiệu quả tài chính khi sử dụng MBA/CĐL 
chất lượng cao: 
 )()( VDPVVDPVNPV cltc (8) 
trong đó: PVtc (VĐ) và PVcl (VĐ) lần lượt là chi phí vòng đời MBA/CĐL tiêu chuẩn và 
chi phí vòng đời MBA/CĐL chất lượng cao tính theo (5). 
 Histogram IRR Tỷ suất hoàn vốn nội tại khi đầu tư sử dụng MBA/CĐL chất 
lượng cao. 
Tỷ suất hoàn vốn nội IRR tại tính theo hàm Excel: 
IRR = IRR(values) (9) 
với tham số biến “values” là dòng tiền (cash flow) hiệu quả tài chính từ năm bắt đầu dự 
án (j = 0) đến năm cuối vòng đời dự án (j = n). 
 Histogram Hiệu quả giảm tổng tổn thất điện năng trong vòng đời n năm khi 
sử dụng MBA/CĐL chất lượng cao: 
)(
1
j
cl
j
tc
n
i
AAASum 
(10) 
trong đó: 
Sum∆A là tổng tiết kiệm tổn thất điện năng trong vòng đời n năm khi sử dụng 
MBA/CĐL chất lượng cao; 
)( jcl
j
tc AA là tiết kiệm tổn thất điện năng năm thứ j trong vòng đời n năm 
khi sử dụng MBA/CĐL chất lượng cao; jcljtc AA  lần lượt là tổn thất điện năng 
năm thứ j của MBA/CĐL tiêu chuẩn và MBA/CĐL chất lượng cao. 
698 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
 Histogram Hiệu quả giảm khí thải CO2 trong vòng đời n năm khi sử dụng 
MBA/CĐL chất lượng cao: 
2 0,4Sum CO Sum A (11) 
trong đó: 
Sum∆A là tổng tiết kiệm tổn thất điện năng trong vòng đời n năm khi sử dụng 
MBA/CĐL chất lượng cao tính theo (10); 
0,4 là hệ số phát khí thải giả thiết 0,4 kg/kWh. 
 Scatter Khảo sát tương quan cặp giá trị NPV & tỷ suất tăng giá điện (e%) 
trong quá trình mô phỏng. 
Hình ảnh các Histograms và Scatter các kết quả mô phỏng trình bày trong hình 3. 
 Hình 3A: Histogram IRR của 10.000 mẫu mô phỏng 
Hình 3B: Scatter NPV vs e% 
của 10.000 mô phỏng 
Hình 3: Kết quả Histogram”, Scatter của các tiêu chí khảo sát của “S_C” 
 Khoảng tin cậy 90% Xác định khoảng tin cậy 90% cho các chỉ tiêu khảo sát: 
NPV; tỷ suất hoàn vốn nội tại IRR; giảm tổn thất điện năng Sum∆A; giảm khí thải 
Sum∆CO2; năm hoàn vốn. Khoảng tin cậy 90% nằm trong giới hạn các giá trị tính theo 
(12A) và (12B). 
Giá trị giới hạn dưới khoảng tin cậy 90% gọi theo hàm Excel 
 =PERCENTILE.EXC(Array,0.05) (12A) 
 Giá trị giới hạn trên khoảng tin cậy 90% gọi theo hàm Excel 
 =PERCENTILE.EXC(Array,0.95) (12B) 
trong đó 
Array mảng hoặc dãy dữ liệu cần xác định vị trí tương đối (%); 
0.5; 0.95 lần lượt là vị trí tương đối của dữ liệu xếp thứ 5 và 95% trong mảng 
Array. 
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0
100
200
300
400
500
600
700
800
8% 11
%
14
%
17
%
20
%
23
%
26
%
29
%
33
%
36
%
39
%
42
%
45
%
48
%
51
%
54
%
57
%
Số mau
IRR (%)
HISTOGRAM TY SUÂT IRR (%)
50
100
150
200
250
300
2.0% 4.0% 6.0% 8.0%
NPV 
tăng giá điện hàng năm (%)
SC AT TER -NPV VS TĂN G G I Á 
Đ IỆN
PHÂN BAN SỬ DỤNG ĐIỆN | 699 
5. KẾT LUẬN 
Đánh giá hiệu quả dự án đầu tư với vòng đời dự án hàng chục năm, luôn luôn gặp 
khó khăn là các dữ liệu đầu vào đều không chắc chắn. Vì thế, việc sử dụng MHNN là 
rất thích hợp vì MHNN mô tả đầy đủ không gian hiệu quả ‘có thể’ và ‘không thể’ của 
dự án mà không cần chi phí tiền bạc để ‘thử nghiệm’ các tình huống bởi vì tất cả các 
tình huống đã được mô phỏng trên máy tính. MHNN giúp chủ đầu tư dự án đưa ra quyết 
định dựa trên phân bố xác suất (histogram) của các chỉ tiêu tài chính NPV, IRR như 
trình bày trong mục “iii Kết quả mô hình Histograms Scatter”: 
Bạn đọc muốn sử dụng “S_C” hoặc quan tâm đến mô hình ngẫu nhiên có thể trao 
đổi với các tác giả qua E mail : tran_trdung@yahoo.com 
TÀI LIỆU THAM KHẢO 
[1] Sáu sigma là gì? Sáu sigma ở Việt Nam Trần Trí Dũng, Tạp chí “Điện lực & Đời sống” số 
155 tháng 3/ 2012. 
[2] Guidance on Life Cycle Cost Analysis Required by Excecutive Order 13123 April 2005 
prepared for DoE Federal Energy Management Program Sieglinde K. Fuller, Economist 
Office of Applied Economics.