Linear group precoding for massive MIMO systems under exponential spatial correlation

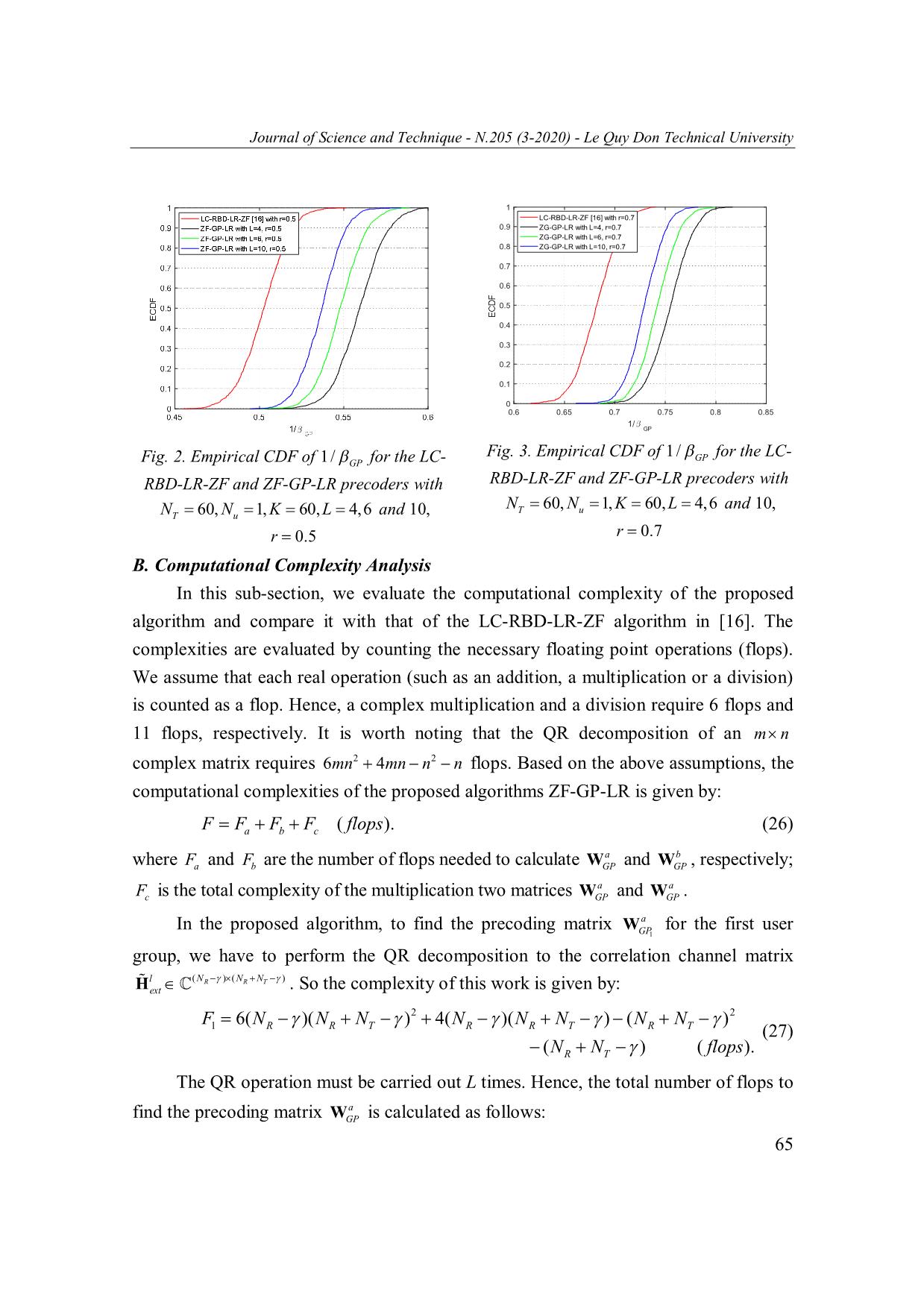
 this sub-section, we evaluate the computational complexity of the proposed 
algorithm and compare it with that of the LC-RBD-LR-ZF algorithm in [16]. The 
complexities are evaluated by counting the necessary floating point operations (flops). 
We assume that each real operation (such as an addition, a multiplication or a division) 
is counted as a flop. Hence, a complex multiplication and a division require 6 flops and 
11 flops, respectively. It is worth noting that the QR decomposition of an m n 
complex matrix requires 6mn2 4 mn n 2 n flops. Based on the above assumptions, the 
computational complexities of the proposed algorithms ZF-GP-LR is given by: 
 F Fa F b F c ( flops ). (26) 
 a b
where Fa and Fb are the number of flops needed to calculate WGP and WGP , respectively; 
 a a
Fc is the total complexity of the multiplication two matrices WGP and WGP . 
 In the proposed algorithm, to find the precoding matrix Wa for the first user 
 GP1
group, we have to perform the QR decomposition to the correlation channel matrix 
 l ()()NNNRRT  
Hext . So the complexity of this work is given by: 
 FNNNNNNNN 6(  )(  )2 4(  )(  ) (  ) 2
 1 RRTRRTRT (27) 
 (NRT N  ) ( flops ).
 The QR operation must be carried out L times. Hence, the total number of flops to 
 a
find the precoding matrix WGP is calculated as follows: 
 65
Journal of Science and Technique - N.205 (3-2020) - Le Quy Don Technical University 
FLFLNNNNNNNN 6(  )(  )2 4(  )(  ) (  ) 2
 1 1 RRTRRTRT (28) 
 (NRT N  ) ( flops ).
 b
 The number of flops to calculated WGP is represented as follows: 
 Fb F2 F 3 F 4 ( flops ), (29) 
 
where F2 is the number of flops to find Hl , F3 is the computational cost for all groups 
  LR
when the ELR-SLB algorithm is adopted to find Hl , and F4 is the total number of 
flops to find the precoding matrix Wb , respectively. Based on the above definitions, 
 ZFl
F2 is calculated as follows: 
 2
 F2 L(8 NTT 2 N  ) ( flops ). (30) 
 In this paper, we apply the ELR-SLB algorithm to convert the channel matrix 
  T  LR
()Hl into the matrix Hl . Therefore, F3 is given by 
 F3 F 5 F 6 Fupdate SLB ( flops ), (31) 
 H 1
where F and F are the number of flops to calculate CHH TT  and 
 5 6 l l 
LR T 
HUHl l l , respectively. Fupdate SLB is computational cost of the ELR-SLB algorithm’s 
update operation, which can only be obtained from the computer simulation. Note that 
every update operation in the ELR-SLB algorithm requires (16γ + 8) flops. The 
computations of ik and i, k in Step 5 and Step 6 in Algorithm 1 need 4 flops and 10 
flops, respectively. Therefore, Fupdate SLB is calculated as follows: 
 Fupdate SLB CUpdate (168) CLamda 4 CDelta 10 ( flops ). (32) 
where CLamda is the number of updates ik , CDelta is the number of updates i, k , 
 ' k
CUpdate is the number of updates tk , ck and c from Step 8 to Step 10 in Algorithm 1. 
  T
Hence, the total number of flops to convert the channel matrix ()Hl into the matrix 
 LR
Hl is calculated as follows: 
 3 2 2
 F3 L(8 16  NT 2  2  N T F update SLB ) ( flops ). (33) 
 The number of flops to find the precoding matrix Wb for all group is given by 
 ZFl
 3 2 2
 F4 L(8 16  NTT 2  2  N ) ( flops ). (34) 
 b
 Therefore, the total number of flops to find the precoding matrix WGP is 
calculated as follows: 
66 
 Journal of Science and Technique - N.205 (3-2020) - Le Quy Don Technical University 
 FFFFLNNLNNF (82 2)(816   3  2 22  2  )
 b2 3 4 T T T T update SLB (35) 
 3 2 2
 L(8 16  NTT 2  2  N ) ( flops ).
 The number of flops for Fc is calculated by 
 3 2
 Fc 8 LN T 2 N T ( flops ). (36) 
 From the above analysis results, the total number of flops for the ZF-GP-LR 
algorithm is given by 
FFFF a b c
 2 2
 LNNNNNNNN 6(RRTRRTRT  )(  ) 4(  )(  ) (  )
 (37) 
 2 3 2 2
 (NNLNNLNNFRT  ) (8 T  2 T  ) (8  16  T 2  2  TupdateSLB )
 3 2 2 3 2
 L(8 16  NTTTT 2  2  N ) 8 LN 2 N ( flops ).
 The complexities of the precoding algorithms ZF-GP-LR and LC-RBD-LR-ZF are 
summarized in Tab. 1. From Tab. 1, we can see that the computational complexity of the 
ZF-GP-LR proposed algorithm is a third-order function of NT . In contrast, the 
computational complexity of algorithm LC-RBD-LR-ZF is a fourth-order function of NT . 
5. Simulation results 
 In this section, we compare both the computational complexity and the system 
performance of the proposed algorithm with those of the LC-RBD-LR-ZF algorithm in [16]. 
 Figure 4 demonstrates the computational complexities of the ZF-GP-LR and LC-
RBD-LR-ZF precoders. In this scenario, NT is varied from 40 to 100 transmit antennas. 
It can be seen from the figure that the complexities of the ZF-GP-LR precoder are 
significantly lower than those of the LC-RBD-LR-ZF. For example, at NNRT 60 
antennas, the complexities of the ZF-GP-LR algorithm with L = 2; 4 and L = 10 are 
approximately equal to 3.04%, 5.52% and 15.21% of the LC-RBD-LR-ZF precoder’s 
complexity, respectively. The computational complexity of the proposed algorithm 
increases as the number of groups L increases. However, the reduction in complexity is 
obtained at the cost of performance degradation as illustrated in the figures 5, 6 and 7. 
 BER performances of the proposed algorithms ZF-GP-LR and the LC-RBD-LR-
ZF precoders are illustrated in Fig. 5 to Fig. 7. In Fig. 5, the system is assumed to work 
in an uncorrelated massive MIMO channel with the following parameters: 
NNRT 60 , and 4-QAM modulation. The channels between the BS and all users are 
assumed to be semi-static Rayleigh Fading channel, the entries are i.i.d with zero mean 
and unit variance. The numbers of user groups for the ZF-GP-LR precoder are L = 4; 6 
 67
Journal of Science and Technique - N.205 (3-2020) - Le Quy Don Technical University 
and 10. As can be seen from Fig. 5, in the low and medium SNR regions, the BER 
curves of the proposed ZF-GP-LR precoder get closer to the LC-RBD-LR-ZF precoder 
as L increases. Specifically, at BER = 10 3 , the proposed algorithm suffers from 
performance degradations of around 0.6 dB, 0.7 dB and 0.9 dB in SNR respectively for 
L = 10; 6 and 4 as compared to the LC-RBD-LR-ZF. However, at sufficiently high 
SNRs, the proposed algorithm provides better system performance than the LC-RBD-
LR-ZF algorithm. 
 In Fig. 6 and Fig. 7, we simulate the system performance in the case exponential 
 1/2
correlation channel at the BS side (i.e., HHRcorr  T ) with the correlation coefficient 
r = 0.5 and r = 0.7. Other parameters are the same as those used to generate Fig. 5. 
Similar to the results in Fig. 5, the results in Fig. 6 and Fig. 7 show that, at low SNR, the 
performance of the proposed ZF-GP-LR precoder approaches that of the LC-RBD-LR-
ZF algorithm when L increases. Besides, at high SNR, the proposed algorithm 
outperforms its LC-RBD-LR-ZF counterpart. From Fig. 6 and Fig. 7, it can also be 
observed that the spatial correlation has an adverse effect on the system performance no 
matter which precoder is employed. 
 Tab. 1. Computational complexity comparison 
 Computational 
 Precoding 
 Complexity (flops) complexity 
 algorithms 
 level 
 2
 KNNNNNNNNNN 6(R u )( R T u ) 4( R u )( R T u )
 LC-RBD- 
 (NNNNNNKNNNN )2 ( ) (8 2 2 )
 LR-ZF R T u R T u T u T u 2
 O() KNTR N 
 algorithm KNNFKNNNNNN(2 ) (8 3 16 2 2 2 2 )
 [16] uT updateLLL u uT u uT
 3 2
 8KNTT 2 N
 2
 LNNNNNN 6(RRTRRT  )(  ) 4(  )(  )
 (NNNNLNN  )2 (  ) (8 2  2  )
 ZF-GP-LR RTRTTT 2
 O() LNTR N 
 algorithm 3 2 2
 LNNF(8 16 T 2  2  T update SLB )
 3 2 2 3 2
 L(8 16  NTTTT 2  2  N ) 8 LN 2 N
 It is worth emphasizing that as the number of antennas at the user side is greater 
 1/2 1/2
than 1, i.e., Nu 1, the correlation channel matrix becomes HRHRcorr R T . In such a 
68 
 Journal of Science and Technique - N.205 (3-2020) - Le Quy Don Technical University 
case, performances of all the precoders under consideration are further degraded. 
However, the behaviors of the BER curves are still the same as those illustrated in Fig. 5 
to Fig. 7. To balance between the computational complexity and system performance, L 
should be selected by NNR/ 2 u when K is an even number. Conversely, K is an odd 
number, L should be selected by the adjacent divisor to the greatest divisor of K. 
 Fig. 4. Compare the complexity of the Fig. 5. The system performance with 
 proposed algorithm and the LC-RBD-LR-ZF NNKLT 60, u 1, 60, 4,6 and 10 
 algorithm in [16]. in the case of uncorrelated channel. 
Fig. 6. The system performance with NT 60, Fig. 7. The system performance with NT 60, 
 NKLu 1, 60, 4,6 and 10 in the case of NKLu 1, 60, 4,6 and 10 in the case of 
 correlated channel use the exponential correlated channel use the exponential 
 correlation chanel model, r 0.5 . correlation chanel model, r 0.7 . 
 69
Journal of Science and Technique - N.205 (3-2020) - Le Quy Don Technical University 
6. Conclusions 
 In this paper, we propose the ZF-GP-LR precoder which is a ZF-based group 
precoding algorithm in combination with the low-complexity ELR-SLB technique to 
improve the BER performance of massive MIMO systems. Performance and complexity 
of the proposed precoder are then investigated in massive MIMO systems using the 
exponential correlation channel model at the BS side. It is shown that the 
ZF-GP-LR precoder has remarkably lower complexity than its LC-RBDLR-ZF 
counterpart. In addition, the BER performance of the proposed ZF-GP-LR approaches 
those of the LC-RBD-LR-ZF algorithm when L increases in the low and medium SNR 
regions. The proposed precoder even outperforms the LC-RBD-LR-ZF in the high SNR 
region in both correlated and uncorrelated channels. As a consequence, the proposed 
ZF-GP-LR precoder can be a potential digital beamforming technique at the base 
stations of massive MIMO systems. 
References 
1. H. Q. Ngo (2015). Massive MIMO: Fundamentals and system designs. Linkӧping 
 University Electronic Press, 1642. 
2. L. Lu, G. Y. Li, A. L. Swindlehurst, A. Ashikhmin, and R. Zhang (Oct 2014). An overview 
 of massive MIMO: Benefits and challenges. IEEE Journal of Selected Topics in Signal 
 Processing, 8(5), pp. 742-758. 
3. T. L. Marzetta (November 2010). Noncooperative cellular wireless with unlimited numbers 
 of base station antennas. IEEE Transactions on Wireless Communications, 9(11), 
 pp. 3590-3600. 
4. T. L. Marzetta (2015). Massive MIMO: An introduction. Bell Labs Technical Journal, 20, pp. 11-22. 
5. T. L. Marzetta, E. G. Larsson, H. Yang, and H. Q. Ngo (2016). Fundamentals of Massive 
 MIMO. Cambridge University Press. 
6. E. G. Larsson, O. Edfors, F. Tufvesson, and T. L. Marzetta (February 2014). Massive 
 MIMO for next generation wireless systems. IEEE Communications Magazine, 52(2), 
 pp. 186-195. 
7. V. P. Selvan, M. S. Iqbal, and H. S. Al-Raweshidy (Aug 2014). Performance analysis of 
 linear precoding schemes for very large multi-user MIMO downlink system. Fourth edition 
 of the International Conference on the Innovative Computing Technology (INTECH 2014), 
 pp. 219-224. 
8. H. Q. Ngo, E. G. Larsson, and T. L. Marzetta (2013). Massive MU-MIMO downlink tdd 
 systems with linear precoding and downlink pilots. 2013 51st Annual Allerton Conference 
 on Communication, Control, and Computing (Allerton), pp. 293-298. 
9. Y. S. Cho, J. Kim, W. Y. Yang, and C. G. Kang (2010). MIMO-OFDM wireless 
 communications with MATLAB. John Wiley & Sons. 
10. Costa (1983). Writing on dirty paper. IEEE Transactions on Signal Processing, 29(3). 
11. O. Bai, H. Gao, T. Lv, and C. Yuen (Oct 2014). Low-complexity user scheduling in the 
 downlink massive MU-MIMO system with linear precoding. in 2014 IEEE/CIC 
 International Conference on Communications in China (ICCC), pp. 380-384. 
70 
 Journal of Science and Technique - N.205 (3-2020) - Le Quy Don Technical University 
12. D. H. N. Nguyen, H. Nguyen-Le, and T. Le-Ngoc (February 2014). Block-diagonalization 
 precoding in a multiuser multicell MIMO system: Competition and coordination. IEEE 
 Transactions on Wireless Communications, 13(2), pp. 968-981. 
13. H. An, M. Mohaisen, and K. Chang (Sept 2009). Lattice reduction aided precoding for 
 multiuser MIMO using Seysen’s algorithm. 2009 IEEE 20th International Symposium on 
 Personal, Indoor and Mobile Radio Communications, pp. 2479-2483. 
14. M. Simarro, F. Domene, F. J. Martínez-Zaldívar, and A. Gonzalez (June 2017). Block 
 diagonalization aided precoding algorithm for large MU-MIMO systems. 2017 13th 
 International Wireless Communications and Mobile Computing Conference (IWCMC), 
 pp. 576-581. 
15. W. Li and M. Latva-aho (March 2011). An efficient channel block diagonalization method 
 for generalized zero forcing assisted MIMO broadcasting systems. IEEE Transactions on 
 Wireless Communications, 10(3), pp. 739-744. 
16. K. Zu and R. C. de Lamare (June 2012). Low-complexity lattice reduction-aided regularized block 
 diagonalization for MU-MIMO systems. IEEE Communications Letters, 16(6), pp. 925-928. 
17. R. N. A. Paulraj and D. Gore (2003). Introduction to space-time wireless communications. 
 New York: Cambridge University Press. 
18. S. L. Loyka (Sep. 2001). Channel capacity of MIMO architecture using the exponential 
 correlation matrix. IEEE Communications Letters, 5(9), pp. 369-371. 
19. C. Windpassinger and R. F. H. Fischer (March 2003). Low-complexity near-maximum-
 likelihood detection and precoding for MIMO systems using lattice reduction. in 
 Proceedings 2003 IEEE Information Theory Workshop (Cat. No. 03EX674), pp. 345-348. 
20. Q. Zhou and X. Ma (February 2013). Element-based lattice reduction algorithms for large 
 MIMO detection. IEEE Journal on Selected Areas in Communications, 31(2), pp. 274-286. 
 TIỀN MÃ HÓA TUYẾN TÍNH THEO NHÓM 
 CHO CÁC HỆ THỐNG MASSIVE MIMO DƯỚI ĐIỀU KIỆN 
 TƯƠNG QUAN KHÔNG GIAN HÀM MŨ 
 Tóm tắt: Trong bài báo này, thuật toán tiền mã hóa tuyến tính theo nhóm trong mô hình 
kênh tương quan hàm mũ được đề xuất cho các hệ thống massive MIMO. Bộ tiền mã hóa đề 
xuất gồm hai thành phần: Thành phần thứ nhất được thiết kế để giảm thiểu can nhiễu từ những 
nhóm người dùng lân cận; Thành phần thứ hai được thiết kế để cải thiện hiệu suất của hệ thống 
bằng cách áp dụng kỹ thuật rút gọn giàn ELR-SLB. Kết quả tính toán và mô phỏng cho thấy 
rằng, bộ tiền mã hóa đề xuất có độ phức tạp tính toán thấp hơn đáng kể so với bộ tiền mã hóa 
LC-RBD-LR-ZF trong khi tỷ lệ lỗi bít (BER) gần tiệm cận với bộ tiền mã hóa LC-RBD-LR-ZF 
khi số lượng nhóm tăng lên. 
 Từ khóa: Hệ thống MU-MIMO; hệ thống massive MIMO; thuật toán tiền mã hóa tuyến 
tính; thuật toán tiền mã hóa phi tuyến; thuật toán rút gọn giàn trong hệ thống MIMO. 
 Received: 28/6/2019; Revised: 03/4/2020; Accepted for publication: 06/4/2020 
  
 71