Khử Gauss-Jordan với vẽ đường cong thực nghiệm đa thức

(Bản scan)

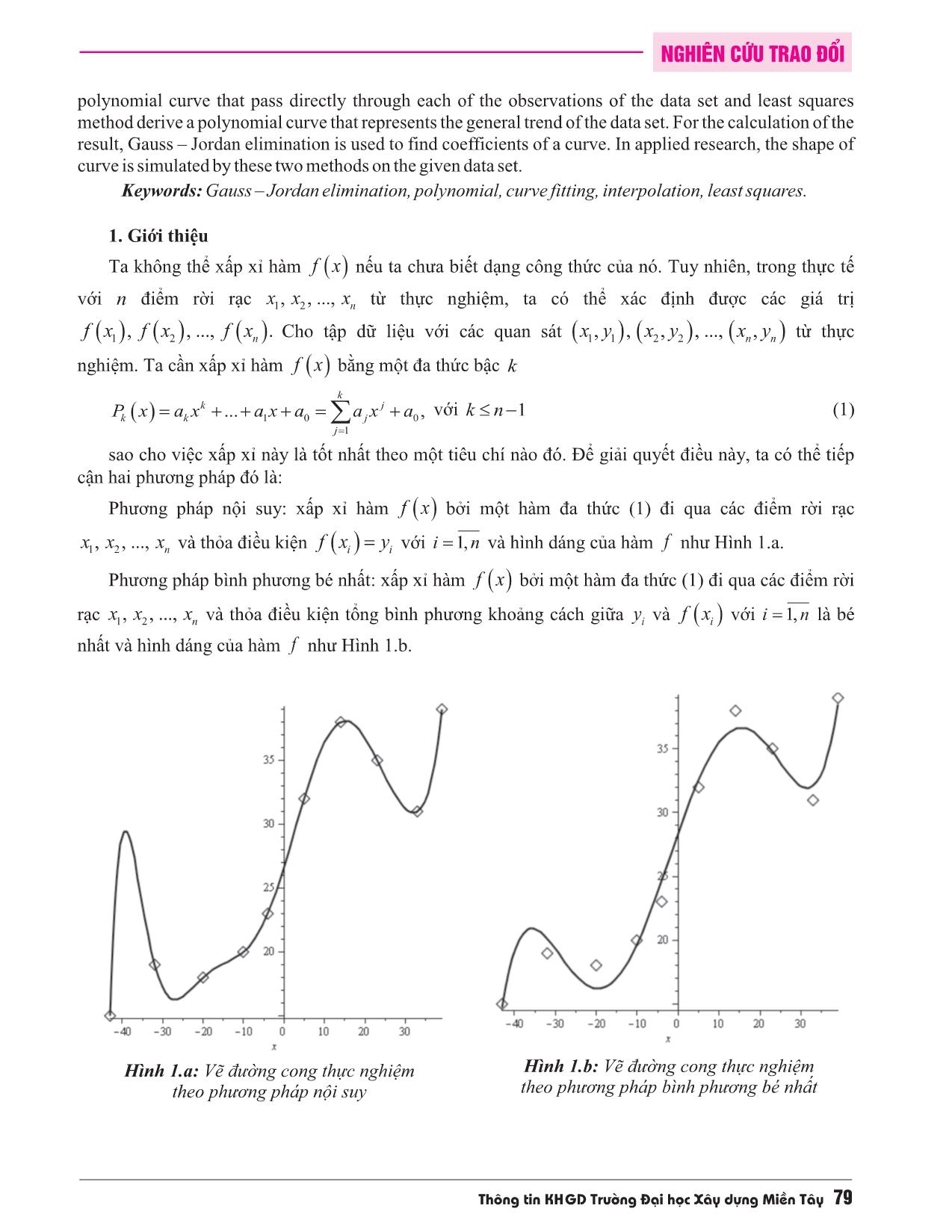
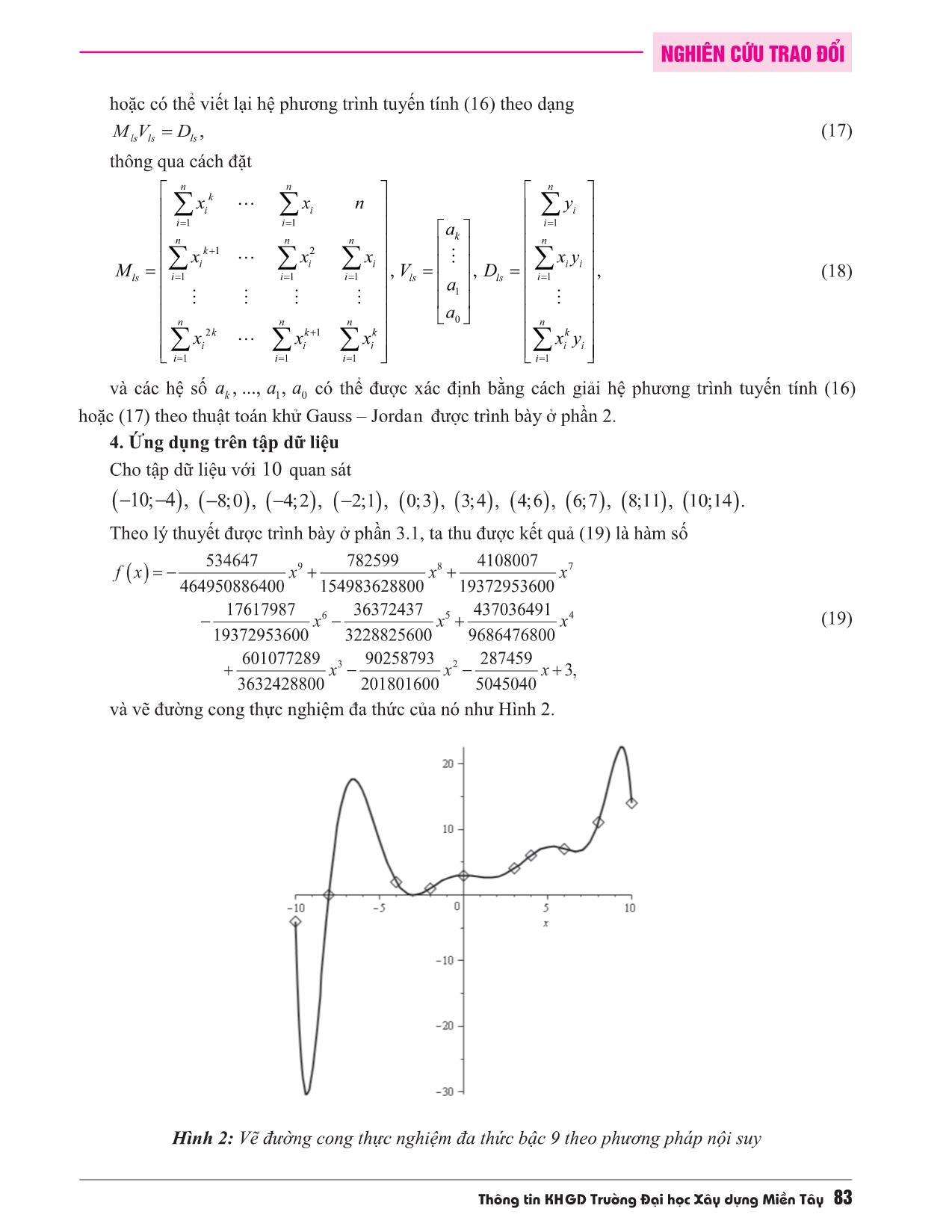
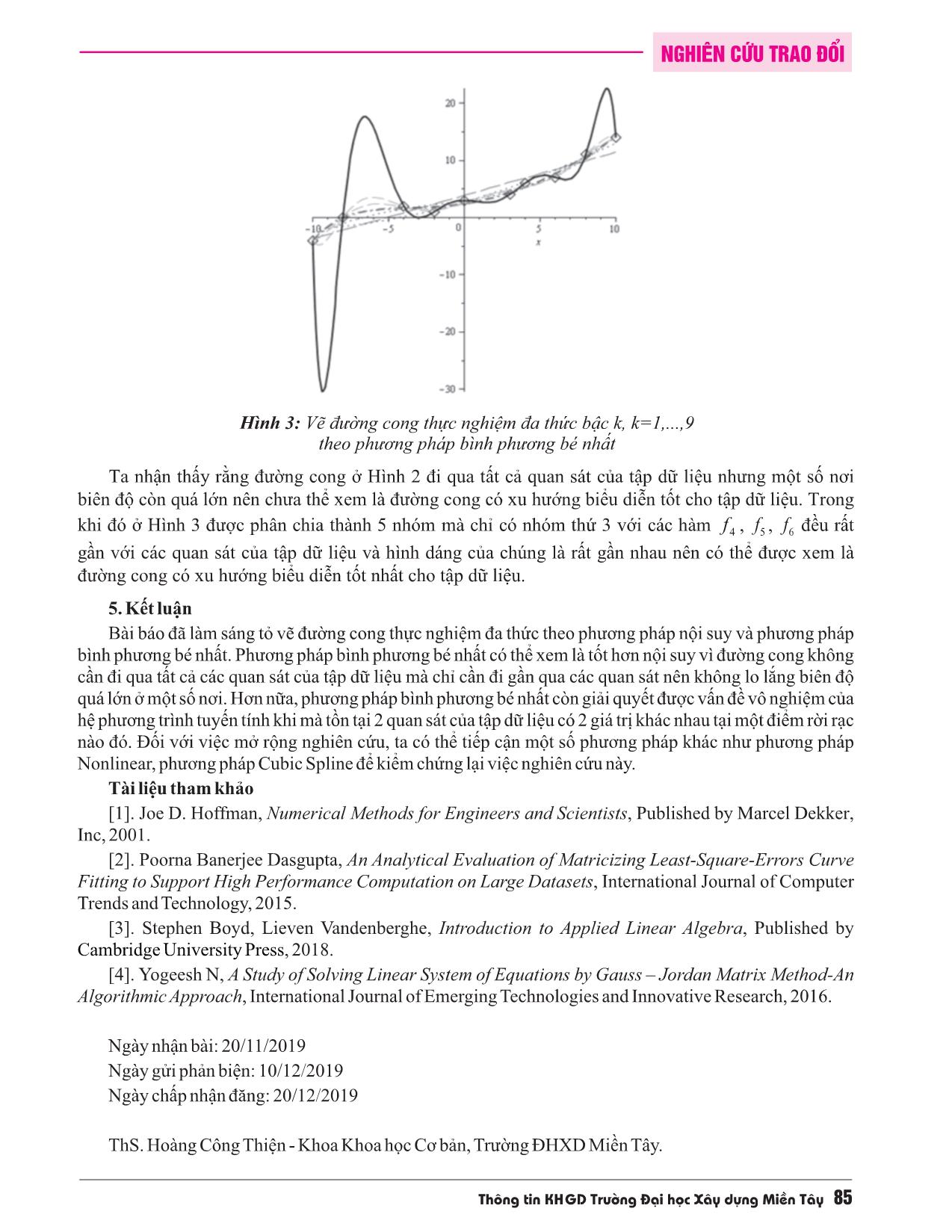
Trong bài báo này, tôi nghiên cứu cách vẽ đường cong thực nghiệm đa thức theo phương pháp nội suy và phương pháp bình phương bé nhất để đi đến giải pháp tìm đường cong thích hợp nhất cho tập dữ liệu. Phương pháp nội suy làm cho khớp đường cong đa thức đi trực tiếp qua từng quan sát của tập dữ liệu và phương pháp bình phương bé nhất suy ra đường cong đa thức thể hiện xu hướng chung của tập dữ liệu. Với việc tính kết quả, khử Gauss-Jordan được sử dụng để tìm các hệ số của đường cong. Trong nghiên cứu ứng dụng, hình dáng của đường cong được mô phỏng bằng hai phương pháp trên tập dữ liệu cho sẵn.