Hội tụ theo xác suất đối với ước lượng mô hình hồi quy phi tham số với sai số ngẫu nhiên độc lập đôi một và có xác suất đuôi nặng

on and Science 
 cKhoa Toán, Trường Đại học Sư phạm - Đại học Đà Nẵng 
 dScience & International cooperation Department, the University of Da Nang - Da Nang University of Education 
 and Science 
 dPhòng Khoa học & Hợp tác Quốc tế, Trường Đại học Sư phạm - Đại học Đà Nẵng 
 (Ngày nhận bài: 30/01/2021, ngày phản biện xong: 18/03/2021, ngày chấp nhận đăng: 25/03/2021) 
Abstract 
In this paper, we study convergence in probability for the estimator of nonparametric regression model based on 
pairwise independent errors with heavy tails. Firstly, we investigate laws of large numbers for sequences of pairwise 
independent random variables with heavy tails. By applying this result, we investigate convergence in probability for 
the estimator of nonparametric regression model. Simulations to study the numerical performance of the consistency for 
the nearest neighbor weight function estimator in nonparametric regression model are given. 
Keywords: Pairwise independence; nonparametric regression; laws of large numbers; the nearest neighbor. 
Tóm tắt 
Trong bài báo này, chúng tôi nghiên cứu sự hội tụ theo xác suất đối với ước lượng của mô hình hồi quy phi tham số với 
sai số ngẫu nhiên độc lập đôi một, có xác suất đuôi nặng. Đầu tiên, chúng tôi sử dụng lý thuyết hàm biến đổi chậm thiết 
lập luật số lớn đối với dãy biến ngẫu nhiên độc lập đôi một, có xác suất đuôi nặng. Áp dụng kết quả thu được, chúng tôi 
thiết lập hội tụ theo xác suất của ước lượng của mô hình hồi quy phi tham số. Ví dụ minh họa và mô phỏng cũng thu 
được hội tụ theo xác suất đối với phương pháp ước lượng láng giềng gần nhất. 
Từ khóa: Độc lập đôi một; hồi quy phi tham số; luật số lớn; láng giềng gần nhất. 
1 This research is funded by the Vietnam Ministry of Education and Training (MOET) under the grant no. B2020-DNA-9 
 Corresponding Author: Le Van Dung; Faculty of Mathematics, the University of Da Nang - Da Nang University of 
Education and Science 
Email: lvdung@ued.udn.vn 
52 T.D. Xuan, N.T.Quyen, N.T.T.An,... / Tạp chí Khoa học và Công nghệ Đại học Duy Tân 02(45) (2021) 51-57 
1. Introduction where Wni()(,,) x  W x x n1 x nn are weighted 
 functions. 
 Let {Xnn ; 1} be a sequence of random 
variables defined on a fixed probability space The above estimator was first proposed by 
( , ,P ), {ani ;1 i n , n 1} be a triangle Stone [11], then Georgiev et al. [4] adapted to 
array of real numbers. There are many useful the fixed design case. Since then, this estimator 
linear statistics based on weighted sums has been studied by many authors. For 
 n example, Georgiev and Greblicki [5], Georgiev 
Sn  a ni X i .One example is the simple 
 i 1 [6], Müller [9] studied for independent errors. 
parametric regression model In recent years, there are many authors to study 
Yi  i  i , where {i ;i 1} is a sequence of for dependent random errors. Wang et al. [12] 
random errors, { i ;i 1} is a sequence of real investigated complete convergence for the 
numbers and  is the parameter of interest. estimator under extended negatively dependent 
The least squares estimator ˆ of  , based on errors, Chen et al. [2] established complete 
 n convergence and complete moment 
a sample of size n, satisfies 
 convergence for weighted sum of asymptotic 
 n
 ˆ 1 negatively associated random variables and 
 n n  i  i . 
 2 i 1 gave its application in nonparametric regression 
  i
 i 1 model, Shen and Zhang [10] obtained complete 
 The aim of this paper is to investigate laws consistency and convergence rate for the 
 n estimator of nonparametric regression model 
of large numbers for S a X of pairwise 
 n ni i based on asymptotically almost negatively 
 i 1
 associated errors. To the best of our knowledge, 
independent with heavy tails {Xnn ; 1}, and 
study convergence in probability for the convergence of the estimator (1.2) in the model 
estimator of nonparametric regression model (1.1) under pairwise independent errors with 
based on pairwise independent errors with heavy tails has not been studied. 
heavy tails. 
 3. Preliminaries 
2. Brief review 
 Let {ann ; 1} and {bnn ; 1} be sequences 
 Consider the following nonparametric of positive real numbers. We use notation 
regression model: abnn instead of 
 Y f( x )  ,1 i n , 0 lim infan / b n l im sup a n/ b n ; 
 ni ni ni (1.1) 
 ann o() b means that limabnn / 0 ; notation 
where x are known fixed design points from a n 
 ni abnn~ is used for limabnn / 1. These 
 n 
compact set A  ℝm, fx() is an unknown notations are also used for positive real 
regression function defined on A ,  i are functions fx() and gx(). The indicator 
random errors. As an estimator of fx( ), the function of A is denoted by IA(). Throughout 
following weighted regression estimator will be this paper, the symbol C will denote a generic 
considered constant (0 C ) which is not necessarily 
 n the same one in each appearance. 
 ˆ
 fn()(), x  W ni x Y ni
 i 1 (1.2) We recall the concept of slowly varying 
 functions as follows. 
 T.D. Xuan, N.T.Quyen, N.T.T.An,... / Tạp chí Khoa học và Công nghệ Đại học Duy Tân 02(45) (2021) 51-57 53 
 Definition 3.1. Let a 0 . A positive Lemma 3.6 ([7]). Let r 0. Suppose that 
measurable function fx() on [;)a is called EX(| |r ) and EY(| |r ) . Then, 
slowly varying at infinity if 
 EXYEXEY(| |r ) 2 r [ (| | r ) (| | r )]. 
 f() tx
 1 as tx for all 0. 4. Results 
 ft()
 For x 0 we denote In the first theorem, we establish the 
 Marcinkiewicz laws of large numbers type for 
log (xx ) max{1,ln( )}, where ln(x ) is the 
 weighted sum of pairwise independent and 
natural logarithm function. Clearly, 
 identically distributed random variables with 
 log (x )
log (xx ), log (log ( )), and so heavy tails. 
 log (log (x ))
on are slowly varying functions at infinity. Theorem 4.1. Let 1 r 2, 0 p r , and 
 let {X , X ; n 1} be a sequence of pairwise 
 Definition 3.2. Let {Xn ; 1} be a n
 n independent and identically distributed random 
sequence of random variables. X converges in 
 n variables with zero mean and 
probability to the random variable X if for 
 P(| X | x ) x r ( x ) , where ()x is a slowly 
every 0, 
 varying function at infinity such that 
 limPXX (|n | ) 0. 1/p r / p 1
 n ()()n o n . Let {ani ;1 i n , n 1} be a 
 p triangle array of real numbers such that 
 Notation: XXn  as n . 
 n
 2
 Lemma 3.3 ([1, 3]). Let 12 r , X be a  ani O( n ). (1.3) 
random variable. If P(| X | x ) x r ( x ) , i 1
where ()x is a slowly varying function at Then, 
 1 n
infinity. Then, a X p 0 as n . 
 n1/ p  ni i
 (a) E(| X | I (| X | x )) x1 r ( x ) . i 1
 Proof. For each n 1 and 1 in, put 
 (b) E(| X |22 I (| X | x )) x r ( x ) . 
 Y X I(| X | n1/ p ), Z X I(| X | n1/ p ),
 ni i i ni i i 
 It is easy to prove the following lemma. n n
 Sn  a ni[ Y ni E ( Y ni )], Sn  a ni[ Z ni E ( Z ni )].
 Lemma 3.4. Let {Xnn ; 1} be a sequence i 1 i 1
of pairwise independent random variables with 
 {Yni ;1 i n }
EX( ) 0 and EX()2 . Then, We have that and 
 n n {Z ;1 i n }
 nn ni is also sequences of pairwise 
 (a) EXEX(|nn |) (| |). independent and identically distributed random 
 ii 11 n
 nn a X S S 
 22  ni i n n
 (b) EXEX(|nn | ) ( ). variables, i 1 . 
 ii 11
 For 0,n 1, we see that 
 Lemma 3.5 (Markov’s inequality, [7]). 
 r n nn1/pp 1/ 
Suppose that EX(| | ) for some r 0, and 1/ p 
 P | ani X i | n P | S n | P | S n | 
let x 0.Then, i 1 22 
 :. II
 EX(| |r ) 12
 P(| X | x )r . I ,
 x For 1 we have 
54 T.D. Xuan, N.T.Quyen, N.T.T.An,... / Tạp chí Khoa học và Công nghệ Đại học Duy Tân 02(45) (2021) 51-57 
 n
 442 2 2
 I1 2 2/pp E | Sn | 2 2/  a ni E [ Y ni E ( Y ni )] 
 nni 1
 nn
 442 2 2 2 1/ p
 2 2/ppani E( Y ni ) 2 2/ a ni E ( X I (| X | n )) 
 nnin 11
 Cn()1/ p
 0 as n .
 2nrp / 1
 Next, we prove I2 0 as n . We have by the Cauchy-Schwarz inequality and (1.3) that 
 nn1/2
 2
 |ani | n a ni Cn . 
 ii 11 
Thus, 
 22n
 I2 1/pp E | Sn | 1/  E | a ni ( Y ni E ( Z ni )) | 
 nni 1
 nn
 2 2 2 1/ p
 1/ppE(| ani Z ni |) 1/ | a ni | E ( X I (| X | n )) 
 nnin 11
 Cn()1/ p
 0 as n .
 nrp/1 
 n
 2 1 2/ p
 We complete the proof. Wni ( x ) O ( n ), (1.1) 
 i 1
 In next theorem, we establish convergence then for any x c() f , 
 ˆ p
in probability of the estimator fxn (), which is ˆ
 fn ( x ) f ( x ) as n , 
defined by (1.2), to the regression function 
fx() in the model (1.1). For any x A,the where cf() denotes all continuity points of the 
following assumptions on weight functions function fx() on A . 
Wxni () will be used. Proof. For any x c() f , it is obvious that 
 n n
 fxfxˆˆ() () Wx () [(()) Efx fx ()].
 (A1) |Wni ( x ) 1| o (1) ; n ni nj n 
 i 1 i 1
 n 1/ p
 Applying Theorem 4.1 with ani n W ni () x , 
 (A2) | |Wni ( x ) | O (1) ; 
 i 1 we have that 
 n
 (A3) p
 n Wni( x ) ni  0 as n . 
 i 1
|Wxfxni ( ) || ( ni ) fxIx ( ) | ( ni xao ) (1) 
i 1 Thus, in order to complete the proof, we 
for any a 0. 
 need to show that 
 Theorem 4.2. Let 12 r , 0 pr. In the ˆ
 E( fn ( x ) f ( x )) 0 as n . 
model (1.1), assume that ( ,i ;1 in ) is a 
sequence of pairwise independent and identically Since x c() f , for any 0, there exists 
distributed errors with zero mean and  0 such that |f ( x ) f ( x ) | holds for all 
 P(| | x ) x r ( x ), x A and xx  . If we choose 
 a (0, ) , then we have 
where ()x is a slowly varying function at 
infinity such that ()()n1/p o n r / p 1 . If 
 T.D. Xuan, N.T.Quyen, N.T.T.An,... / Tạp chí Khoa học và Công nghệ Đại học Duy Tân 02(45) (2021) 51-57 55 
 n
 ˆ
 |(()Efxfxn ())|  Wxfx ni ()() ni fx ()
 i 1
 n
 |Wni ( x ) || f ( x ni ) f ( x ) | I ( x ni x a )
 i 1
 nn
 |Wxfxni ( ) || ( ni ) fxIxxa ( ) | ( ni ) Wx ni ( ) 1 | fx ( ) | 
 ii 11
 nn
 |Wxni ( ) | |Wxfx ni ( ) || ( ni ) fxIxxa ( ) | ( ni )
 ii 11
 n
 Wni (x ) 1 | f ( x ) | 0 as n followed by 0 (by (A1)-(A3)).
 i 1
 ˆ
 Hence, E( fn ( x ) f ( x )) 0 as n . 
 5. Example and numerical simulation x i/ n
 Taking ni for 1 in. For any 
 Let  and  be two independent complex ||xx ||xx 
 1 2 x (0,1) , we write n1 , n2 ,... 
random variables, which are uniformly 
 ||xx 
distributed on the unit circle nn as 
 {z a bi :| z | 1}, ()x be the CDF of |x x | | x x | | x x |, 
 n,(),(),() R12 x n R x n Rn x
the standard normal distribution. For n 1, set 
 if |x x | | x x | , then ||xx is 
 1 arg()n 1 ni nj ni
e  1() 12. It follows by Janson considered to be in front of ||xx when 
 n 22 nj
 xxni nj . 
[8] that {enn ; 1} is a sequence of pairwise 
 2/3
independent standard normal random variables. Let r 3/ 2, p 6 / 5 . Let knn [] be the 
 2/3
Let  be a symmetric random variable with the integer part of n , we define 
tail probability 1
 , if |xni x | | x n,() R x x |
 1 Wx() k kn
 P(| | x ) for x 0, ni n 
 r 
 xxlog ( ) 1 0, otherwise.
where 12 r . Let F be the distribution It is easy to see that all the conditions (A1)-
function of  . For n 1, we define (A3) are satisfied and (1.4) holds. From 
 1
 nn 0.1Fe ( ( )). Theorem 4.2, for any x (0,1) , we obtain 
 We have that { ;n 1} is a sequence of ˆ p
 n fn ( x ) f ( x ) as n . 
pairwise independent and identically distributed 
 Let f( x ) 3 x2 if x [0,1] and fx( ) 0 
random variables with zero mean and 
 otherwise. Taking the sample sizes n as 200, 
P(| | x ) x r / log ( x ) . Noting that 
 i 500, 800 and 1600. For each sample size, we 
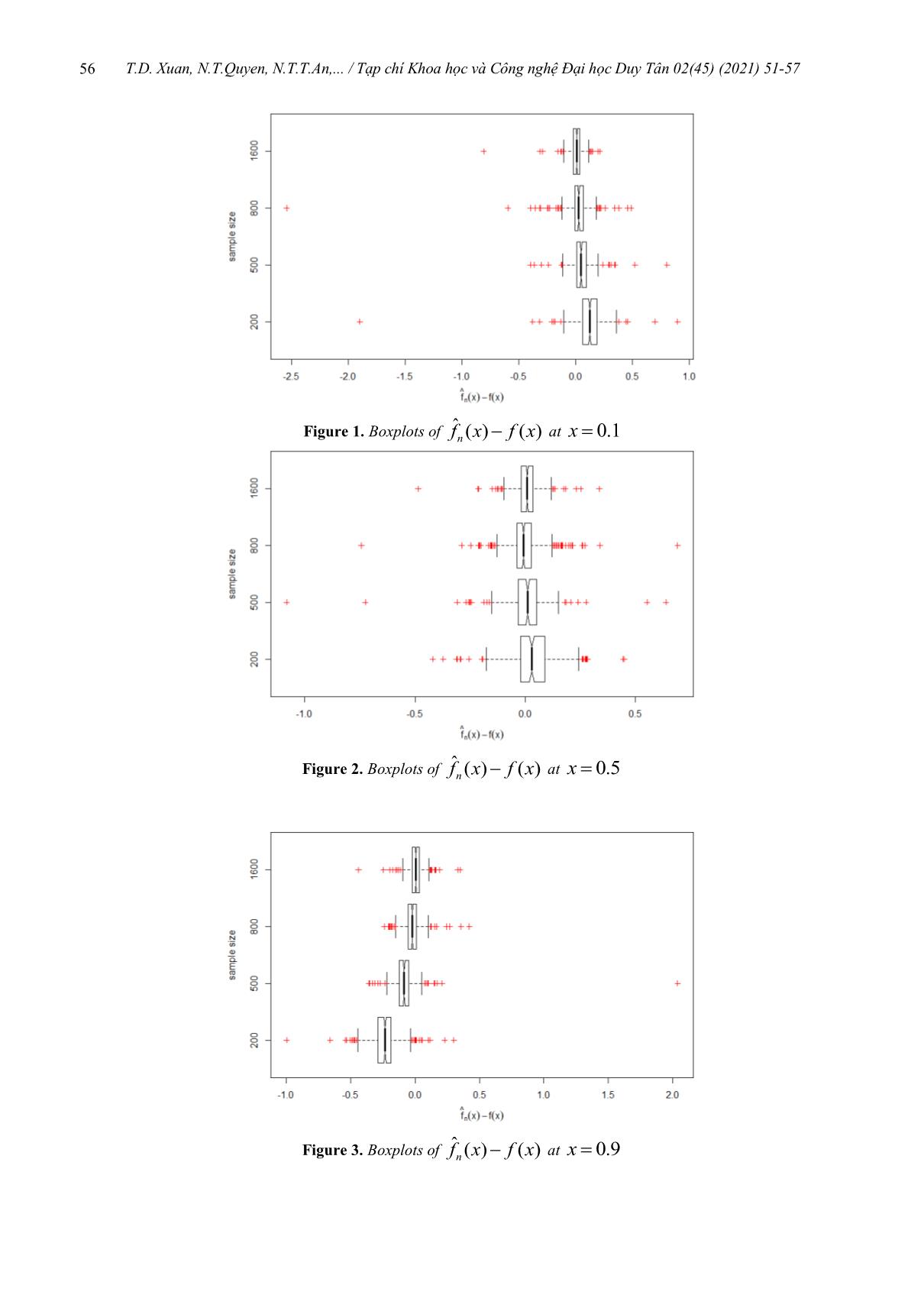
Var() . ˆ
 use R software to compute fn ()() x f x for 
 Consider the nonparametric regression model: 300 times and get the corresponding boxplots 
 Yni f( x ni )  ni ,1 i n , by taking x 0.1, 0.5, 0.9 and the sample size 
where fx() is an unknown continuous function n as 200, 500, 800 and 1600 respectively in 
 Figures 1, 2, 3; the values of mean and root 
on [0,1], (ni ;1 in ) has the same 
 mean square error (rmse) at , x 0.5 
distribution as (12 ,  ,... n ). 
 and x 0.9 in Table 1. 
56 T.D. Xuan, N.T.Quyen, N.T.T.An,... / Tạp chí Khoa học và Công nghệ Đại học Duy Tân 02(45) (2021) 51-57 
 ˆ
 Figure 1. Boxplots of fn ()() x f x at x 0.1 
 ˆ
 Figure 2. Boxplots of fn ()() x f x at x 0.5 
 ˆ
 Figure 3. Boxplots of fn ()() x f x at x 0.9 
 T.D. Xuan, N.T.Quyen, N.T.T.An,... / Tạp chí Khoa học và Công nghệ Đại học Duy Tân 02(45) (2021) 51-57 57 
 [4] Georgiev A. A. et al., 1985, Local properties of 
 Table 1. The mean and rmse of fxˆ () 
 n function fitting estimates with applications to system 
 n x fx() mean rmse identification. In: Grossmann W (ed) Mathematical 
 th
 0.1 0.03 0.147 0.207 statistics and applications, volume b, proceedings 4 
 Pannonian symposium on mathematical statistics, 4–
 200 0.5 0.75 0.781 0.113 10, September, 1983, Bad Tatzmannsdorf, Austria. 
 0.9 2.43 2.190 0.263 Reidel, Dordrecht, 141-151. 
 0.1 0.03 0.082 0.113 [5] Georgiev A. A., Greblicki W., 1986, Nonparametric 
 500 0.5 0.75 0.753 0.120 function recovering from noisy observations, J Stat 
 0.9 2.43 2.350 0.164 Plan Inference, 13(1), 1-14. 
 0.1 0.03 0.047 0.181 [6] Georgiev A. A., 1988, Consistent nonparametric 
 multiple regression: the fixed design case, J 
 800 0.5 0.75 0.749 0.098 Multivar Anal 25(1), 100-110, 
 0.9 2.43 2.410 0.074 [7] Gut, A., 2013, Probability: A Graduate Course, 
 0.1 0.03 0.033 0.073 second ed., Springer. 
 1600 0.5 0.75 0.759 0.065 [8] Janson S., 1988, Some pairwise independent 
 0.9 2.43 2.440 0.065 sequences for which the central limit theorem fails, 
 Stochastics, 23, 439-448. 
References [9] Müller H.G., 1987, Weak and universal consistency 
 of moving weighted averages, Period Math Hung, 
[1] Hồ Minh Châu, Lê Văn Dũng, Lương Thị Mỹ Hạnh, 18(3), 241-250. 
 2018, Luật số lớn đối với tổng ngẫu nhiên có trọng [10] Shen A. and Zhang S., 2020, On Complete 
 số các biến ngẫu nhiên độc lập đôi một có mô men consistency for the estimator of nonparametric 
 cấp r vô hạn, Tạp chí Khoa học Trường Đại học Sư regression model based on asymptotically almost 
 phạm - ĐH Đà Nẵng, 30(04), 66-72. negatively associated errors, Methodology and 
[2] Chen Zh., Lu C., Shen Y., Wang R. and Wang X., Computing in Applied Probability. DOI: 
 2019, On complete and complete moment 10.1007/s11009-020-09813-x 
 convergence for weighted sums of ANA random [11] Stone C.J., 1977, Consistent nonparametric 
 variables and applications, Journal of Statistical regression, Ann Stat 5, 595-645. 
 Computation and Simulation. DOI: [12] Wang X.J., Zheng L.L., Hu Sh., 2015, Complete 
 10.1080/00949655.2019.1643346 consistency for the estimator of nonparametric 
[3] Dung L.V., Son T.C. and Hai Yen N.T., 2018, Weak regression models based on extended negatively 
 laws of large numbers for sequences of random dependent errors, Stat: J Theor Appl Stat., 49(2), 
 variables with infinite rth moments, Acta 396-407. 
 Mathematica Hungarica, 156, 408-423.