Giải phương trình đạo hàm riêng sử dụng mạng Neural nhân tạo

o) hàm∈ Ω cấp, hai của phương trình Poisson sử dụng sai phân trung tâm biến 
đổi ta có một hệ gồm (M+1)2 phương trình với (M+1)2 ẩn. Giải hệ này ta tính được giá trị tại các nút lưới 
của lưới sai phân. 
2.1 Lưới sai phân và hàm lưới 
 Hình 1: Lưới sai phân hữu hạn 
 Chọn số tự nhiên M>0. Chia miền thành các ô lưới như sau: 
 Chia đoạn [a,b] thành M đoạn bằng nhau bởi M+1 điểm chia có tọa độ , 
 Ω
là độ dài đoạn chia, với i : 1 M+1 
  =  +( − 1)ℎ ℎ = 
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 25 
 Chia đoạn [c,d] thành M đoạn bằng nhau bởi M+1 điểm chia có tọa độ , 
là độ dài đoạn chia. Mỗi điểm tương ứng với một nút lưới , với i, j : 1 M+1 
  =  +( − 1)ℎ ℎ = 
 Một hàm số xác định tại các nút lưới gọi là hàm lưới. Giá trị của hàm lưới tại nút lưới ký 
 ,  (, )
hiệu xác định bởi :  
  
 , i, j : 1 M+1.  ,  
 ,
 Tập gọi là tập nút trong 
 , = , 
 Tập ,     gọi là tập nút biên 
 Ω ={ ,  | ,   ∈ Ω } 
  
2.2 LượcΩ đồ, sai={ phân,  |,  ∈ Ω }
 Từ phương trình   , để xấp xỉ đạo hàm cấp 
  (,)  (, )
 và   
hai theo biến tại điểm +  , chúng=  (ta sử,  dụng),  <công <thức, sai< phân < trung tâm ta được
    
    ,   (3) 
 , , , , , ,
 − 2 +   − 2 +  ,
 Thay  +  =  
 (3)ℎ vào (2) và biến đổi thànhℎ dạng bài toán sai phân hữu hạn hạn
 (4) 
 
  ℎ
 , , , , ,  ,  (5) 
  +  +  +  − 2(1 + ) = ℎ  ,  =  
 ℎ 
 (6) 
 , = , :1  +1
 (7) 
 , = , :1  +1
 (8) 
 ,  
  =  ( ), : 1  + 1 và . 
 Từ phương trình (4), cho ta mối quan hệ giữa bốn nút lưới xung quanh của Giải hệ phương 
trình đại số tuyến tính (4-8)= ta  xác( định), được: 1 giá trị+ của1 hàm lưới với . 
 , ,
3 MẠNG NEURAL TRUYỀN THẲNG MỘT LỚP ẨN ĐỂ, GIẢI , PDE∶1 (NNM) +1 
3.1 Mạng truyền thẳng một lớp ẩn. 
 Nhiều kiến trúc khác nhau của mạng neural đã và đang phát triển mạnh. Tuy nhiên người ta đã chứng 
minh được rằng mạng neural truyền thẳng một lớp ẩn (single hidden layer feedfordward neural network - 
SLFN) có thể xấp xỉ một hàm bất kỳ nếu số nút ẩn và hàm truyền được chọn một cách thích hợp [7]. 
 Kiến trúc SLFN giải PDE với d nút ở lớp nhập, N nút ở lớp ẩn và 1 nút ở lớp xuất có thể minh họa như 
hình 2: 
 Hình 2: Kiến trúc tiêu biểu của mạng neural một lớp ẩn (SLFN) giải PDE 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
26 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 
 Với là ngõ vào, là véc tơ trọng số kết nối từ các nút nhập j đến nút 
ẩn thứ m,   , là độ lệch (bias) của nút ẩn thứ m, là vector trọng số kết 
  = [, ,, ] ∈  
nối từ lớp ẩn thứ m đến nút xuất ,  tích vô hướng của hai vecto và , là hàm truyền 
  ,     
(trong nghiên cứu=[ này, tác giả,, sử dụng] hàm sigmoid). Ứng với mỗi vector đầu vào ngõ xuất được 
    
xác định  ∙    (.)
  
  (9) 
3.2 Nghiệm PDE sử =dụng  SLFN(  ∙  + )
 
 Cho phương trình đạo hàm riêng cấp hai với có dạng tổng quát [9]: 
  (10) 
  
thỏa điều kiện,  (biên), ∇ (boundaryu(), ∇  (conditions) = 0 ,  – ∈BCs) Ω ⊂ Dirichlete, ,  ∈ với là nghiệm 
của phương trình (10) cần xác định. Biên của miền kí hiệu là . 
  
 Nghiệm gần đúng của (10) có thể được xác định bằng cách = chia( lướ,,i mi)ền∈  và, ( và) tìm giá trị 
của tại các nút lưới thuộc miền Ω . RõΩ ràng việc tìm giá trị u tại các nút lưới 
thuộc đưa về( giải) hệ phương trình (11) Ω Ω
  Ω =  ∈ Ω;  =1,, 
 Ω , (11) 
 
 phải thỏa điều  kiện,  biên, ∇Dirichlet.u, ∇  = 0 ,  ∈ Ω
 Thay vì xác định giá trị tại các nút lưới thuộc bằng cách giải hệ phương trình, gọi là 
nghiệm gần đúng của phương trình (14), trong đó p là tham số có thể điều chỉnh sao cho cực tiểu hàm lỗi 
(12) Ω (, )
 (12) 
  
 () =  (, (, ), ∇(, ), ∇ (, )) , 
 thỏa điều kiện∈ biên Dirichlet. 
 Nghiệm gần đúng được xác định sử dụng SLFN thỏa điều kiện biên Dirichlet có thể viết 
 
dưới dạng tổng của 2 số hạng [9], trong đó là trọng số của SLFN được thay bởi . 
 
  (, ) , (13) 
  , 
trong( ,đó , ) = () + () (, , , ) (14) 
với giá trị đầu vào, 
 (, , ) =  ()
   trọng số của SLFN,   là ngõ xuất của mạng neural , A(x) hàm không chứa 
      
trọng số=[ của ,SLFN 1] và thoả điều kiện =[ biên ,Dirichlet, ,,  F(]x), là =[hàm không,  ,, cần ]thoả,  điều= [ kiện, ] biên∈R Dirichlet.,  = 
[Trong, ,, bài báo] này nghiệm gần đúng (, , ) của (10) được xác định sử dụng SLFN với thuật toán 
lan truyền ngược để cực tiểu hàm lỗi (12) qua việc điều chỉnh trọng số của mạng. 
 Như vậy việc xác định nghiệm  gần( , đúng,  ) phương trình (10) tương ứng với việc xác định 
 , với ,  , 
3.3 ∗ ∗ ∗ ∗ SLFN 
  Gradient của ngõ xuất đối với đầu vào, trọng số của 
 (Để, cực, tiểu) hàm  lỗi =(12) SLFN được( huấn, ) luyện = để điều chỉnh( trọng, ) số của mạng sao cho với mỗi giá 
trị ta có G( xấp xỉ với giá trị 0. Một trong các tiếp cận phổ biến để tìm thỏa điều kiện trên là 
dựa trên giảm gradient. Trong đó, ngõ xuất và các đạo hàm của ngõ xuất đối với ngõ vào, các 
  
trọng số của mạng ) cần phải được xác định. , 
3.3.1 Gradient ngõ xuất đối với ngõ vào của( SLFN, ,  )
 Xét kiến trúc mạng neural SLFN như hình 2, với đầu vào , ngõ xuất của 
mạng được xác định  
  = [, ,, ] ∈ 
 , (15) 
 
 = ∑ ( )
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 27 
với 
 
     
Khi đó ta= có: ∑   +  
    (16) 
  ()
        
  =         +    =     ,
với     
 ()
Tương( tự) với đạo hàm bậc k của O theo biến ngõ vào được tính theo công thức 
  = 
 
 
  (17) 
  
   ()
 với =  ,  là đạo hàm bậc k của hàm sigmoid 
  
 ()
 Hơn nữa, = ta( có thể)  dễ dàng kiểm chứng [9]  
 (18) 
    
    ()
      
 với     =     (19) 
    
   
3.3.2 Gradient= ∏ ngõ xuất, Λ =đối∑ với các trọng số của SLFN 
 Dựa vào vế trái công thức (18) ta thấy đạo hàm của ngõ xuất đối với ngõ vào tương đương với một 
mạng truyền thẳng 1 lớp ẩn (SLFN). Ngõ xuất của SLFN này gọi là với SLFN có trọng số kết nối từ 
lớp nhập đến nút ẩn thứ m là , độ dịch nút ẩn thứ m là , trọng số kết nối nút ẩn thứ m đến ngõ xuất 
 
là hàm truyền các nút ẩn là như vậy . Khi đó từ công thức (18) ta có: 
  
 ()  ()
   ,  = ∑  (20) 
  ()
 = 
  (21) 
  ()
    
  =   
  (22) 
 
  ()    ()
         
  =     +        
3.4 Các bước xác định nghiệm của PDE, bằng NNM với điều kiện biên Dirichlet 
3.4.1 Nghiệm phương trình Poisson sử dụng SLFN 
 Để minh họa cho việc xác định nghiệm của PDE bằng NNM trong bài báo này chọn phương trình 
Poisson hai chiều có dạng [9] : 
 , v i (23) 
   ớ
  (,)  (, )
  
thoả điều kiện+ biên Dirichlet= ( , )  ∈ [0,1],  ∈ [0,1], 
 , 
 (24) 
 (0, ) = (), (1, ) = () . 
      
 Nghiệm NNM của phương trình( ,(023) )= xác  định( ) ,bằng( SLFN, 1) = thỏa ( (24)) có dạng [9]: 
 (25) 
 (, , , ) = (, ) + (1 − )(1 − )(, , , ), 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
28 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 
 (26) 
 với (, ) = (1 − )() + ()
 + (1 − ){() 
 Để xác định nghiệm− [(1 − gần) đúng(0 ) + (1)] }c+ủa phương{() trình (23) tham số cần được điều chỉnh 
bằng cách huấn luyện− [(1 SLFN− ) sao( 0cho) + hàm lỗi(1 )(27)]} đạt giá trị nhỏ nhất. 
 (, , ) , 
 , (27) 
  
   (, )  (, )
    
(, , , ) =  ∑{  +  − (, )}
v i , 
 ớ 
  (, ) (28) 
 
   , v i n s m u hu n luy n m ng. 
  ( ,  ) ∈ [0,1] x [0,1]ớ ố ẫ =ấ ệ ạ
  (, )
3.4.2 Các bước xác  định nghiệm NNM sử dụng thuật toán huấn luyện lan truyền ngược 
  |   ,    
 Bước 1. Khởi tạo n mẫu , j = 1,,n . 
 Bước 2. Khởi tạo giá trị ngẫu nhiên trọng số mạng neural . 
   
 Bước 3. Tính giá trị ngõ xuất=(  của,  SLFN) theo công thức (9). 
 , 
 Bước 4. Tính giá trị của  theo công thức (17), (20-22). 
 (,,,) (,,,)
 Bước 5. Cập nhật vector trọng số của mạng theo công thức (29). 
  ,  
 = - η , η hệ số học 
 (,,,) (29) 
  =  - , 
    hệ số học
 (,,,)
 trong đó Wk , k là cập nhật trọng số bước lặp thứ k , là hàm lỗi được tính theo công 
     
 thức (27). 
 Bước 6. Nếu < ( hằng số dương) nhảy( ,đến, Bước, ) 7, ngược lại quay lại Bước 3 
 Bước 7. Thay bộ trọng số đã tính ở Bước 5 vào công thức (25) để tính nghiệm NNM của phương 
 trình (23). Bộ trọng(  số,   này,  , sẽ ) dùng  kiểm tra để đánh giá nghiệm NNM so với nghiệm FDM của 
 phương trình (23). 
4 KẾT QUẢ THỰC NGHIỆM 
 Trong phần này chúng tôi minh họa cách xác định nghiệm NNM của PDE bằng thuật giải đã trình bày 
trong mục 3.32 và so sánh với nghiệm FDM. Lỗi nghiệm NNM được xác định : 
 Lỗi nghiệm NNM = Nghiệm giải tích – Nghiệm NNM (30) 
 Lỗi nghiệm FDM = Nghiệm giải tích – Nghiệm FDM 
Xét phương trình PDE sau 
 (31) 
  
    
với , với điều + kiện biên= 0 Dirichlet 
  
 0≤  ≤1,0≤  ≤1 (32) 
 (0, ) = 2, (1, ) = 0 
Nghiệm giải tích của phương trình (30) thỏa điều kiên biên Dirichlet (31): 
 (, 0) = 2, (, 1) = 0
 (33) 
 1
Dựa vào (dạng,  nghiệm) = SLFN( sinhcủa [phương2(1 − trình)] (25),( 2nghiệm) + NNMsinh [ 2của( 1(30)−  có) ]dạng: ( 2)
 sinh 2 
 (34) 
 1 2
Trong đó (, ,  ,được) = tính( dự,  vào) + công(1 thức−  (2)6)( 1 − )(, , )
 (35) 
 (, )
 (, ) = (1 − )2 + (1 − )2
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 29 
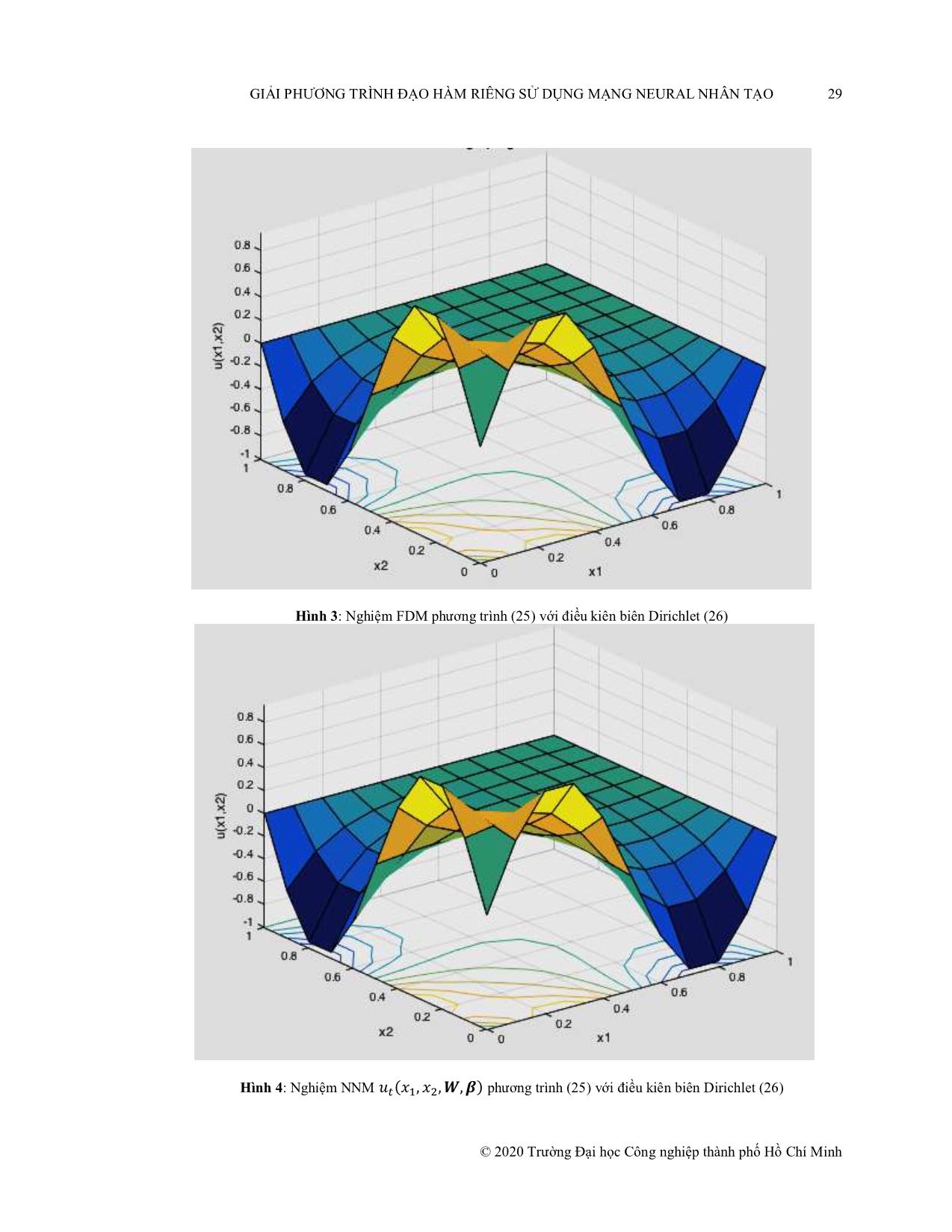
 Hình 3: Nghiệm FDM phương trình (25) với điều kiên biên Dirichlet (26) 
Hình 4: Nghiệm NNM phương trình (25) với điều kiên biên Dirichlet (26) 
 (, , , )
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
30 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 
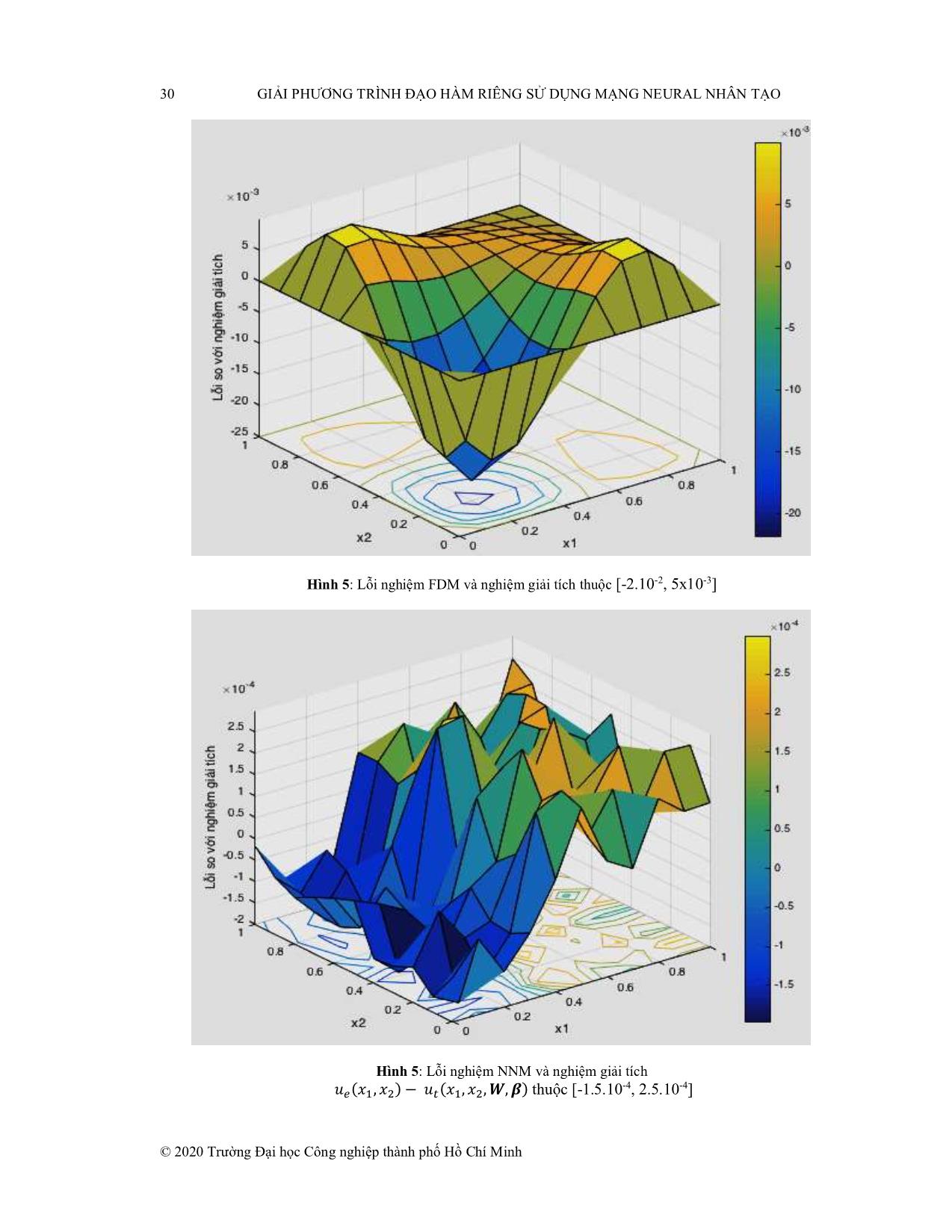
 Hình 5: Lỗi nghiệm FDM và nghiệm giải tích thuộc [-2.10-2, 5x10-3] 
 Hình 5: Lỗi nghiệm NNM và nghiệm giải tích 
 thuộc [-1.5.10-4, 2.5.10-4] 
 (, ) − (, , , ) 
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 31 
 Để xác định nghiệm gần đúng phương trình (31-32) giải bằng NNM sử dụng SLFN với 10 nút ẩn dựa 
trên thuật toán huấn luyện lan truyền ngược, tập huấn luyện cho SLFN được chọn 121 điểm (bằng cách 
chia lưới [0,1]x[0,1] dọc theo ). Từ đó xác định bộ trọng số (W ) của SLFN và xác định được 
 . Biểu đồ nghiệm FDM, nghiệm NNM, lỗi giữa nghiệm giải tích so với FDM, lỗi giữa 
nghiệm giải tích so với NNM của,  thực nghiệm trên được thể hiện như , Hình 3, Hình 4, Hình 5, Hình 6 
tương( ,ứng.,  , )
 Dựa vào hình 5 cho thấy lỗi nghiệm NNM của PDE sử dụng NNM so với nghiệm giải 
tích thuộc đoạn [-1.5.10-4, 2.5.10-4] . 
 Dựa vào hình 6 cho thấy lỗi nghiệm FDM của PDE sử dụng ( FDM,  ,so ,với) nghiệm giải tích 
 (,có )lỗi thuộc đoạn [-2.10-2, 5x10-3]. 
 Kết quả cho thấy nghiệm gần đúng PDE giải bằng NNM chính xác hơn nghiệm gần đúng giải bằng 
FDM.( , ) 
5 KẾT LUẬN 
 Trong bài báo này, chúng tôi trình bày phương pháp NNM để giải phương trình Poisson hai chiều với 
điều kiện biên Dirichle sử dụng mạng truyền thẳng một lớp ẩn với thuật toán huấn luyện mạng lan truyền 
ngược. Các tham số của SLFN được cập nhật theo công thức (24) bởi một số bước lặp. Với phương pháp 
sử dụng NNM thì nghiệm cho kết quả chính xác hơn so với phương pháp FDM. Các 
tham số cần tìm của NNM ít hơn rất nhiều so với việc tính giá trị tại các nút lưới của lưới sai phân sử 
dụng FDM và yêu cầu về bộ nhớ( ,tính, toán,  )ít hơn hẳn so với FDM [10] . Phương pháp NNM để giải PDE 
có dạng nghiệm tổng quát có thể áp dụng cho phương trình vi phân, hệ phương trình vi phân và các PDE 
dạng khác [9]. Hướng phát triển tiếp theo của nghiên cứu là sử dụng mạng tích chập (convolutional neural 
network) để giải PDE nhằm tăng độ chính xác nghiệm của PDE và sử dụng mạng học sâu (deep learning) 
để giải các dạng PDE bậc cao. 
LỜI CẢM ƠN 
 Bài báo được thực hiện với sự hỗ trợ từ quỹ đề tài nghiên cứu khoa học trường đại học Công nghiệp 
TP HCM, mã số 182.CNTT01/HD-DHCN 
TÀI LIỆU THAM KHẢO 
[1] Ricardo, H.J., A modern introduction to differential equations2009: Academic Press. 
[2] Boyce, W.E., R.C. diprima, and D.B. Meade, Elementary differential equations and boundary value problems. 
 Vol. 9. 1992: Wiley New York. 
[3] Smith, G.D., Numerical solution of partial differential equations: finite difference methods1985: Oxford 
 university press. 
[4] Dill, E.H., The finite element method for mechanics of solids with ANSYS applications2011: CRC press. 
[5] Demuth, H., M. Beale, and M. Hagan, MATLAB User’s Guide, version 4.0: Neural network toolbox. 
 Mathworks Inc.: Natick, MA, USA, 2005. 
[6] Shirvany, Y., M. Hayati, and R. Moradian, Multilayer perceptron neural networks with novel unsupervised 
 training method for numerical solution of the partial differential equations. Applied Soft Computing, 2009. 
 9(1): p. 20-29. 
[7] Huang, G.-B. And H.A. Babri, Upper bounds on the number of hidden neurons in feedforward networks with 
 arbitrary bounded nonlinear activation functions. IEEE Transactions on Neural Networks, 1998. 9(1): p. 224-
 229. 
[8] Thomas, J.W., Numerical partial differential equations: finite difference methods. Vol. 22. 2013: Springer 
 Science & Business Media. 
[9] Lagaris, I.E., A. Likas, and D.I. Fotiadis, Artificial neural networks for solving ordinary and partial differential 
 equations. IEEE transactions on neural networks, 1998. 9(5): p. 987-1000. 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
32 GIẢI PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG SỬ DỤNG MẠNG NEURAL NHÂN TẠO 
[10] Rudd, K., G. Di Muro, and S. Ferrari, A constrained backpropagation approach for the adaptive solution of 
 partial differential equations. IEEE transactions on neural networks and learning systems, 2014. 25(3): p. 571-
 584. 
 Ngày nhận bài: 03/05/2019 
 Ngày chấp nhận đăng: 20/06/2019 
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh