Evaluate error correction performance of binary repeat accumulate code and Quasi cyclic low-density parity-check code in 5G new-radio

encoder block diagram. 
 3. QUASI-CYCLIC LDPC CODE 
 Several attempts have been made to build the QC code over GF(2) [12, 19]. A code is 
called quasi-cyclic when with a cyclic movement of a codeword with a displacement of 1, a 
codeword is obtained. The simplest quasi-cycle is the coded row, which has weigh L, described 
by the parity check matrix [10, 20]. 
 (3.1) 
 where 1, 2,  , 퐿 are binary 푣 × 푣 circulant matrices 
 QC code has been studied by Townsend and Weldon [19], Chen [15] and after its 
invention, there are many other research articles such as [10, 11, 19] gradually improving QC 
code. According to the information and coding theory, one of the things to keep in mind when 
designing channel coding is Hamming distance. In simple terms, Hamming distance or 
maximum distance is the difference between codewords. When the decoder executes, the 
larger the Hamming distance, the less likely it is to convert the correct codeword to another 
 26 
Evaluate error correction performance of binary repeat accumulate code and quasi cyclic 
codeword that also satisfies the error check condition in LDPC. The maximum distance of the 
QC code mentioned in [19] shows that the QC code is a good code with Hamming distance 
much improved compared to other algorithms. 
 In matrix presented in Equation 3.1, in sub-matrices always exists a reversible matrix, 
called 퐿. Thus, we can infer the generator matrix based on the formula 3.2 [12, 13, 20]. 
 (3.2) 
 Besides, due to the unique characteristics of the code, circulant matrices can be 
 푣−1
represented by the polynomial as follows: ( ) = 0 + 1 + ⋯ + 푣−1 with indicators 
 0, 1,  , 푣−1 are the first row in the 푖 matrix. Thus, instead of dealing with matrices, we 
can replace signal processing on algebraic equations. Furthermore, we can find the inverse 
matrix corresponding to finding an inverse equation is mentioned in the study of Baldi et al. [21]. 
 Because QC code has its characteristics in construction, with a codeword length or a 
specified code rate, there will be a separate matrix standard for the QC code. In which, 3GPP is 
one of the associations that regulates communication structures, such as the QC code matrix for 
WiMax, DVBS2, 5G standards [3, 8, 14, 22, 23]. Thus, instead of the traditional method of 
building the parity matrix and using a complex Gauss-Jordan elimination to create a generator 
matrix , with a definite structure QC code makes the LDPC encoding faster and simpler. 
 Nowadays, due to traditional standards and large information transmission needs, it is 
difficult to create the matrix . Therefore, instead of giving the matrix , we build a base 
graph matrix (BG matrix) containing the shift parameters, this is also known as the QC code 
block. Each translation index in BG will correspond to a unit matrix of size 푍 with the number 
of shifts. The next section will show how to build BG in the 5G standard. 
 4. 5G-NR LDPC BASE GRAPH CONSTRUCTION 
 Information message for the 5G network is large, thus the decoding is complicated. 
Instead of giving a very large matrix, it is replaced by a base matrix, and from this base 
matrix with 푍 , size of each unit matrix, we will deduce matrix . There are two types of base 
matrices BG1 and BG2, which are adopted for 5G LDPC codes. 
 . 
 Figure 5. Base graph selection based on block size and code rate [23] 
 27 
Nguyen Hong Hoa, Tran Thi Bich Ngoc, Hoang Trang 
 These two matrices have a similar structure. BG1 with a matrix size of 46 × 68 entries is 
designed for large transport block, information lengths up to 8448, and code rates from 1/3 to 
8/9, while BG2 with a matrix size of 42 × 52 entries is targeted for smaller block lengths and 
code rates from 1/5 to 2/3. 
 The construction on BG1 and BG2 is mentioned in [6, 14, 22] with general following steps: 
 - Step 1: Base on the size of message 퐾 and code rate 푅, we can determine the type of 
 base graph. 
 - Step 2: We find the number of information circulant columns 퐾 with given 퐾 and 푅. 
 - Step 3: We determine suitable shift coefficient 푍 by searching the following table: 
 Table 1. Choose 푍 base on index 푖퐿푆 table [6]. 
 Set index (iLS) Set of lifting sizes (Z) 
 0 {2, 4, 8, 16, 32, 64, 128, 256} 
 1 {3, 6,12, 24, 48, 96, 192, 384} 
 2 {5, 10, 20, 40, 80, 160, 320} 
 3 {7, 14, 28, 56, 112, 224} 
 4 {9, 18, 36, 72, 144, 288} 
 5 {11, 22, 44, 88, 176, 352} 
 6 {13, 26, 52, 104, 208} 
 7 {15, 30, 60, 120, 240} 
 - Step 4: Searching standard table and the result will be BG for 5G-NR LDPC. 
 1
 In this paper, data will be used on BG2 with 퐾 = 2304, 퐾 = 1944 and code rate = 
 2
 2
and , respectively for both QC and RA codes. 
 3
 5. SIMULATION RESULTS AND DISCUSSION 
 This section will build the RA code and QC code based on the method mentioned in 
sections 2 and 3. To examine the quality of both RA and QC codes over GF(2), we encode the 
same message with both RA and QC codes with binary phase shift keying (BPSK) modulation 
and transmit over the AWGN channel, and use the Min Sum LDPC decoder in 10 iterations at 
receiver, conducted by MATLAB software. For QC-LDPC, BG2 was generated based on the 
3GPP standard mentioned in section 4, and for RA LDPC, the interleaver was randomly 
selected because, for the 5G standard, the size of data is large. 
 Figure 6 shows the performances of both algorithms at the same code length = 2304 
 1
and rate 푅 = . In general, we can see that when transmitting information over 5G standard, 
 2
if the information is encoded by QC code, the performance will be much higher than that of 
the RA code, approximately Δ ≈ 3.10−5 ÷ 10−5 ≈ 3 푡푖 푒푠 at SNR = 3 dB, and deviation 
distance between QC code and RA code is almost maintained during the change of SNR. If 
we consider the quality difference between RA and QC code, it can be seen that the larger the 
SNR, the higher the QC quality compared to RA code. 
 28 
Evaluate error correction performance of binary repeat accumulate code and quasi cyclic 
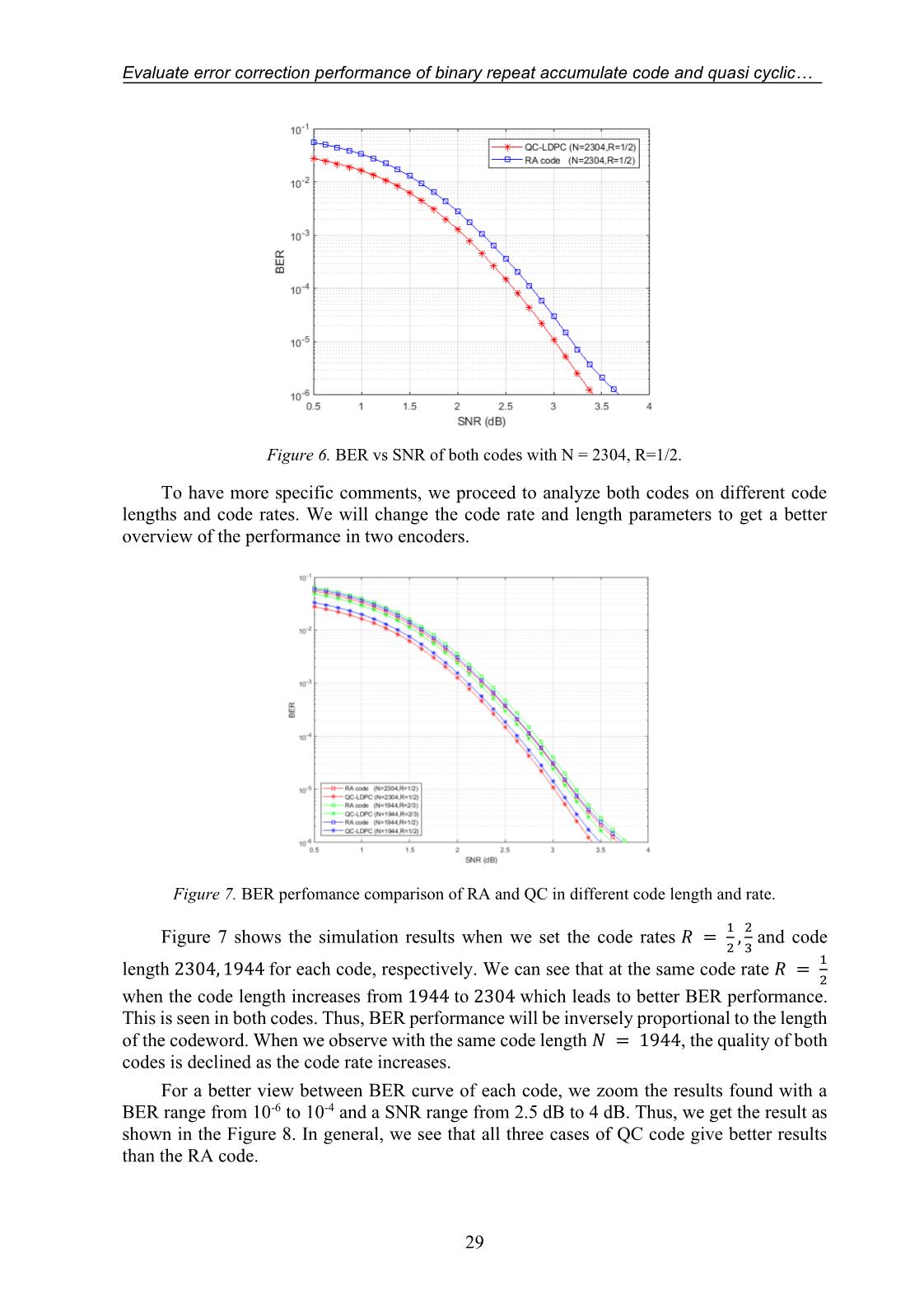
 Figure 6. BER vs SNR of both codes with N = 2304, R=1/2. 
 To have more specific comments, we proceed to analyze both codes on different code 
lengths and code rates. We will change the code rate and length parameters to get a better 
overview of the performance in two encoders. 
 Figure 7. BER perfomance comparison of RA and QC in different code length and rate. 
 1 2
 Figure 7 shows the simulation results when we set the code rates 푅 = , and code 
 2 3
 1
length 2304, 1944 for each code, respectively. We can see that at the same code rate 푅 = 
 2
when the code length increases from 1944 to 2304 which leads to better BER performance. 
This is seen in both codes. Thus, BER performance will be inversely proportional to the length 
of the codeword. When we observe with the same code length = 1944, the quality of both 
codes is declined as the code rate increases. 
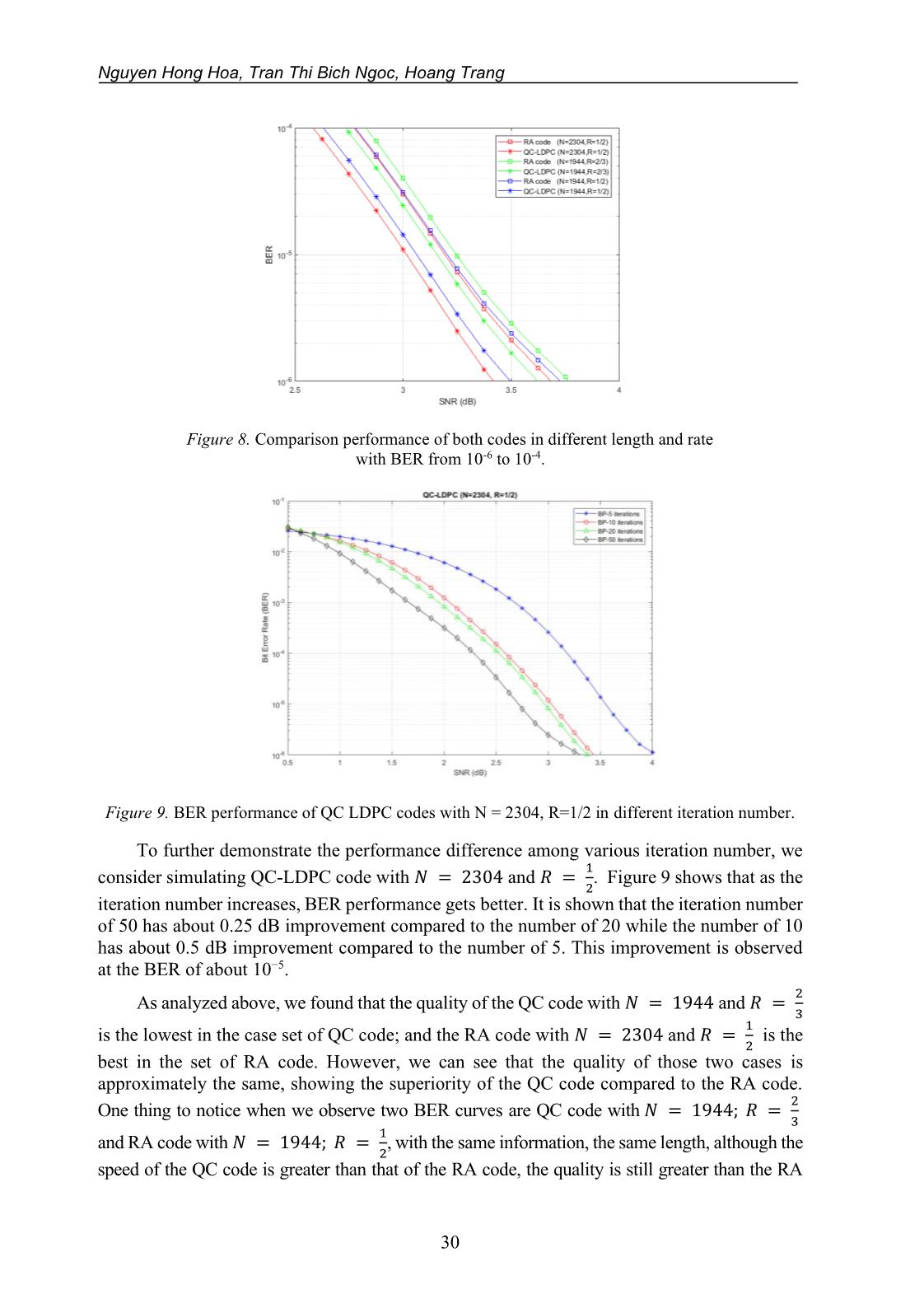
 For a better view between BER curve of each code, we zoom the results found with a 
BER range from 10-6 to 10-4 and a SNR range from 2.5 dB to 4 dB. Thus, we get the result as 
shown in the Figure 8. In general, we see that all three cases of QC code give better results 
than the RA code. 
 29 
Nguyen Hong Hoa, Tran Thi Bich Ngoc, Hoang Trang 
 Figure 8. Comparison performance of both codes in different length and rate 
 with BER from 10-6 to 10-4. 
 Figure 9. BER performance of QC LDPC codes with N = 2304, R=1/2 in different iteration number. 
 To further demonstrate the performance difference among various iteration number, we 
 1
consider simulating QC-LDPC code with = 2304 and 푅 = . Figure 9 shows that as the 
 2
iteration number increases, BER performance gets better. It is shown that the iteration number 
of 50 has about 0.25 dB improvement compared to the number of 20 while the number of 10 
has about 0.5 dB improvement compared to the number of 5. This improvement is observed 
at the BER of about 10−5. 
 2
 As analyzed above, we found that the quality of the QC code with = 1944 and 푅 = 
 3
 1
is the lowest in the case set of QC code; and the RA code with = 2304 and 푅 = is the 
 2
best in the set of RA code. However, we can see that the quality of those two cases is 
approximately the same, showing the superiority of the QC code compared to the RA code. 
 2
One thing to notice when we observe two BER curves are QC code with = 1944; 푅 = 
 3
 1
and RA code with = 1944; 푅 = , with the same information, the same length, although the 
 2
speed of the QC code is greater than that of the RA code, the quality is still greater than the RA 
 30 
Evaluate error correction performance of binary repeat accumulate code and quasi cyclic 
code. Thus, with the same message, one of the ways to increase the code rate while keeping the 
performance or even better is to change the encoding method from an RA encoder to a QC encoder. 
 6. CONCLUSION 
 In this paper, the construction of the RA code and QC code on the algebraic method over 
GF(2) is presented. We implement comparisons of the quality of both codes in the case of 
changes in code rate and code length. When considering the same speed and length, it is clear 
that the BER performance of the QC code will give better quality than the RA code 
approximately 3 times. Whereas if we look at the overview on the different rates and different 
lengths of the QC and RA codes, we find that with the same code length N, we can increase 
the code rate but keep the BER performance when changing the encoder from RA code into 
QC code. The code rate plays a very important role in the digital information age. Although 
the complexity of the QC code is higher than the RA code due to the implementation of matrix 
multiplication, the performance of the QC code is much better than the RA code, so the 
engineer needs to consider choosing the QC code or RA code. Choosing the appropriate 
algorithm for encryption will contribute to increased efficiency in information transmission in 
5G, a standard that Vietnam wants to achieve in Industry 4.0. 
 REFERENCES 
 1. Gallager R. - Low-density parity-check codes, IRE Transactions on information 
 theory 8 (1) (1962) 21-28. 
 2. Dielissen J., Hekstra A., and Berg V. - Low cost LDPC decoder for DVB-S2, 
 Proceedings of the Design Automation & Test in Europe Conference, Munich (2006) 1-6. 
 3. ETSI EN 302 307 V1. 1.1 (2004-01) European Standard (Telecommunications series) 
 Digital Video Broadcasting (DVB) Second generation framing structure, channel 
 coding and modulation systems for Broadcasting, Interactive Services, News 
 Gathering and other broadband satellite applications. 
 4. Jain S. and Koshti R. - Performance Improvement of IEEE 802.22 WRAN with 
 Different FEC Codes, 2013 International Conference on Machine Intelligence and 
 Research Advancement (2013) 430-434. 
 5. Kim K.J., Myung S., Park S.-I., Lee J.Y., Kan M., Shinohara Y., Shin J-W., Kim J. 
 - Low-density parity-check codes for ATSC 3.0, IEEE Transactions on Broadcasting 
 62 (1) 189-196. 
 6. ETSI TS 138 212 V15.2.0 (2018-07) 5G; NR; Multiplexing and channel coding (3GPP 
 TS 38.212 version 15.2.0 Release 15), ETSI (2018). 
 7. Abbasfar A., Divsalar D., Yao K. - Accumulate-repeat-accumulate codes, IEEE 
 Transactions on Communications 55 (4) 692-702. 
 8. Zhang W., Chen S., Bai X., Zhou D. - A full layer parallel QC-LDPC decoder for 
 WiMAX and Wi-Fi, 2015 IEEE 11th International Conference on ASIC (ASICON) 
 (2015) 1-4. 
 9. MacKay D.J.C. - Information theory, inference and learning algorithms, Cambridge 
 University Press (2002). 
 10. Fossorier M.P. - Quasicyclic low-density parity-check codes from circulant permutation 
 matrices, IEEE Transactions on Information Theory 50 (8) (2004) 1788-1793. 
 11. Xu H., Feng D., Luo R. and Bai B. - Construction of quasi-cyclic LDPC codes via 
 masking with successive cycle elimination, IEEE Communications Letters 20 (12) 
 (2016) 2370-2373. 
 31 
Nguyen Hong Hoa, Tran Thi Bich Ngoc, Hoang Trang 
 12. Skjærbæk T.H. - Quasi-cyclic codes, Master Thesis at Aalborg Universitet (2010). 
 13. Ryan W., Lin S. - Channel codes: classical and modern, Cambridge University Press (2009). 
 14. Ahmadi S. - 5G NR: Architecture, technology, implementation, and operation of 3GPP 
 new radio standards, Academic Press (2019). 
 15. Chen C.L., Peterson W.W., and Weldon E.J. - Some results on quasi-cyclic codes, 
 Information and Control 15 (5) (1969) 407-423. 
 16. Zhang K., Yin L., and Lu J. - Construction of repeat accumulate codes with 
 superimposed structured interleavers, Proceeding of the 9th WSEAS International 
 Conference on Multimedia System & Signal Processing (2009) 108-113. 
 17. Johnson S.J. - Iterative error correction: Turbo, low-density parity-check and repeat-
 accumulate codes, Cambridge University Press (2009). 
 18. Tram Thi Bao Nguyen, Tuy Nguyen Tan, Hanho Lee - Efficient QC-LDPC encoder 
 for 5G new radio, Electronics 8 (6) (2019) 668. 
 19. Townsend R., Weldon E. - Self-orthogonal quasi-cyclic codes, IEEE Transactions on 
 Information Theory 13 (2) (1967) 183-195. 
 20. Gulliver T.A., Bhargava V.K. - A (105,10,47) binary quasi-cyclic code, Applied 
 Mathematics Letters 8 (4) (1995) 67-70. 
 21. Baldi M., Bambozzi F., Chiaraluce F. - A class of invertible circulant matrices for QC-
 LDPC codes, 2008 International Symposium on Information Theory and Its 
 Applications (2008) 1-6. 
 22. Richardson T., Kudekar S. - Design of low-density parity check codes for 5G new 
 radio, IEEE Communications Magazine 56 (3) (2018) 28-34. 
 23. Chelikani N. - 5G-NR DL-SCH LDPC Channel Coding Base Graph selection and 
 Coding Procedure (2019); Available at: https://www.linkedin.com/pulse/5g-nr-dl-
 sch-ldpc-channel-coding-base-graph-selection-chelikani 
 TÓM TẮT 
 ĐÁNH GIÁ CHẤT LƯỢNG SỬA LỖI KHI SỬ DỤNG MÃ REPEAT ACCUMULATE 
 VÀ MÃ QUASI CYCLIC LOW-DENSITY PARITY CHECK TRONG MẠNG 5G 
 Nguyễn Hồng Hòa1*, Trần Thị Bích Ngọc1,2, Hoàng Trang1 
 1Trường Đại học Bách khoa - Đại học Quốc gia TP.HCM 
 2Trường Đại học Giao thông vận tải TP.HCM 
 *Email: hoa.nguyen.raven7@hcmut.edu.vn 
 Mã LDPC (Low-density parity check) là mã sửa sai mật độ thấp đã được chọn dùng cho 
mạng 5G vì khả năng tốc độ xử lý cao, hiệu suất về diện tích và năng lượng cao. Mã LDPC đã 
được chứng minh cho kết quả sửa lỗi tiến tới giới hạn Shannon kể từ khi LDPC được phát 
minh ra, có nhiều thuật toán mã hóa cũng được công bố, trong đó có mã Quasi Cyclic LDPC 
(mã QC) và mã Repeat Accumulate LDPC (mã RA). Hai mã này được sử dụng nhiều trong 
việc mã hóa và giải mã bởi độ phức tạp của chúng thấp. Trong bài báo này, nhóm tác giả tiến 
hành xây dựng hai mã trên, khảo sát và phân tích hiệu suất của cả hai mã với yêu cầu ứng dụng 
chiều dài khối lớn trong mạng 5G. 
Từ khóa: Mã LDPC, mã RA, mã QC, chuẩn 5G, hiệu suất BER so với SNR. 
 32