Đường cong bậc 2

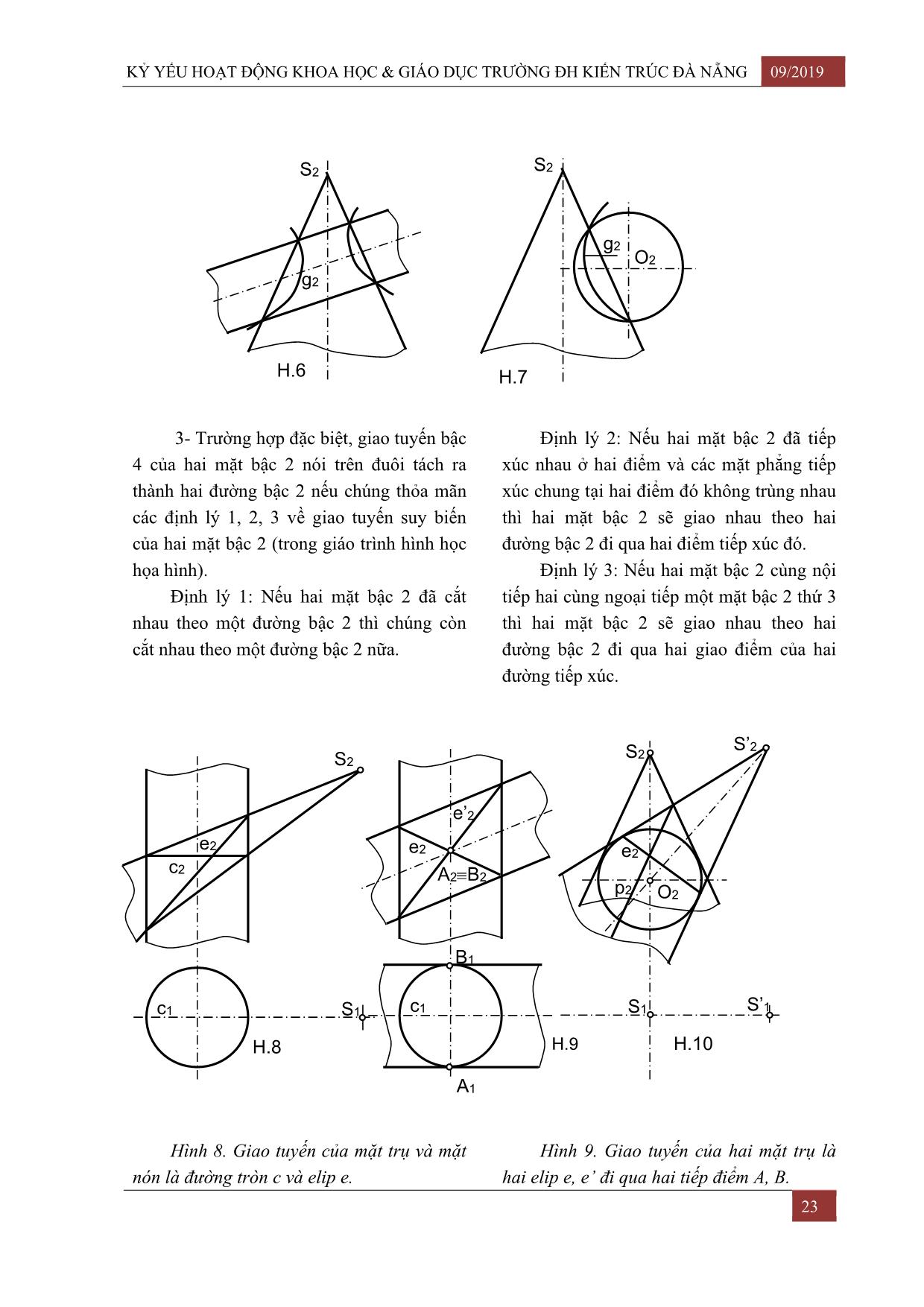
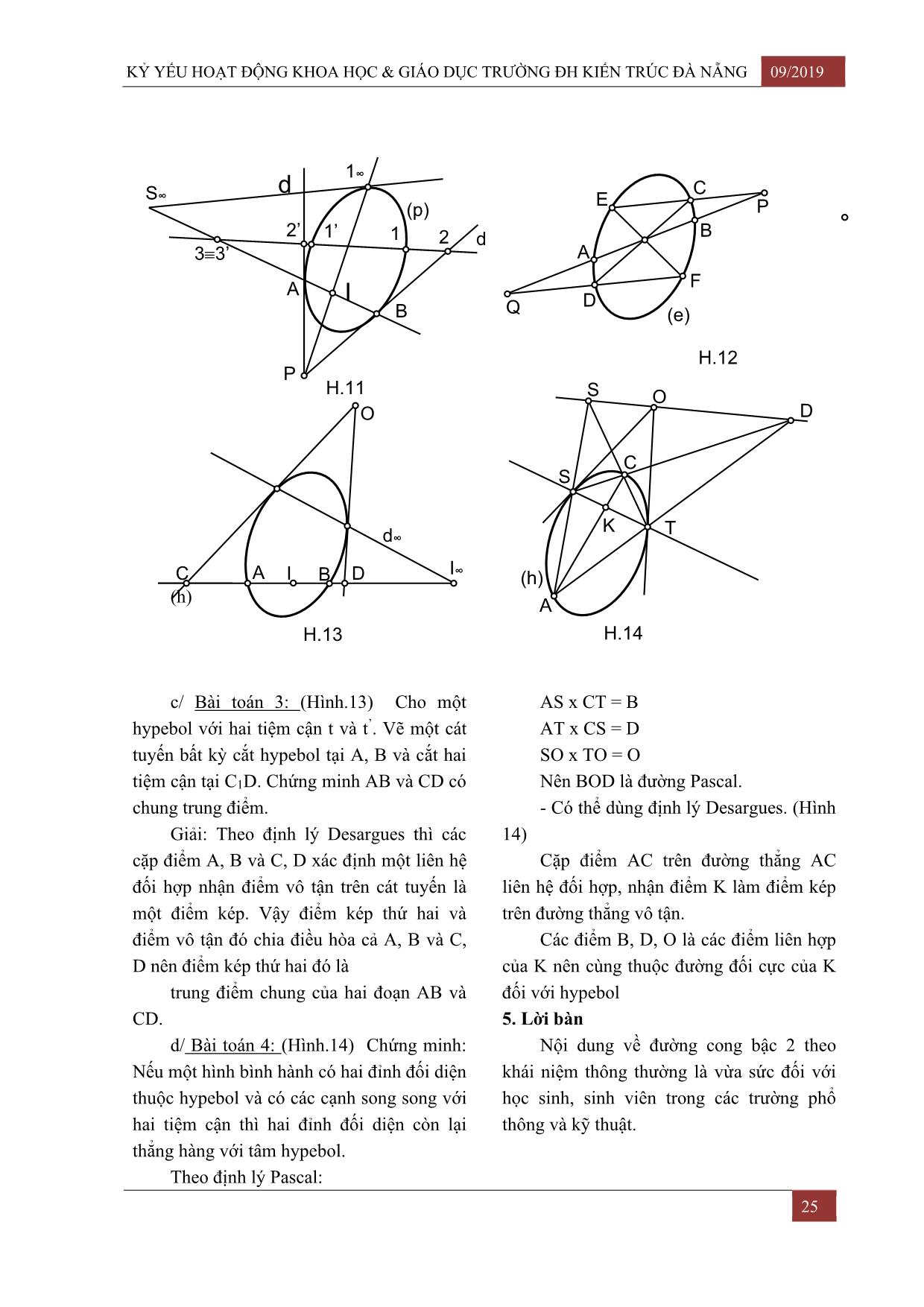
KỶ YẾU HOẠT ĐỘNG KHOA HỌC & GIÁO DỤC TRƯỜNG ĐH KIẾN TRÚC ĐÀ NẴNG 09/2019 
 ĐƯỜNG CONG BẬC 2 
 TS. Nguyễn Tư Đôn (*) 
 Đường cong bậc 2 là đường cong đại số được phổ biến trong các môn hình học phẳng, 
 hình học giải tích, hình học họa hình, vẽ kỹ thuật và nhiều môn hình học khác trong chương 
 trình trung học và đại học. 
 Có ba đường bậc 2: elip, parabol và hypebol. 
 1. Định nghĩa thông thường - Trong mặt phẳng, parabol là quỹ tích 
 1.1. Elip (Hình.1) các điểm M cách đều một điểm F và một 
 - Trong mặt phẳng, elip là quỹ tích các đường thẳng d cố định. 
 điểm M sao cho tổng khoảng cách từ M đến MF = MH 
 hai điểm cố định F, F’ bằng hằng số. F là tiêu điểm và d là đường chuẩn. 
 MF + MF’ = 2a - Nếu chọn các trục X, Y như hình vẽ, 
 F và F’ là hai tiêu điểm. phương trình của parabol là Y2 = 2pX trong 
 O là điểm giữa của FF’ nên OF = OF’ = đó p là khoảng cách từ F đến d và được gọi 
 c là tham số của parabol. 
 - Nếu đặt trục X ≡ FF’ và trục Y ⊥ X 1.3. Hypebol (Hình.3) 
 tại O, ta có phương trình của elip là: - Trong mặt phẳng, hypebol là quỹ tích 
 X2 Y2
 + = 1 với b2 = a2 = c2. các điểm M sao cho hiệu các khoảng cách từ 
 a2 b2
 ’
 Đoạn thẳng AB = 2a, CD = 2b M đến hai điểm cố định F, F bằng hằng số. 
 Vì a > b nên AB được gọi là trục dài, (hằng này bé hơn đoạn FF’) 
 ′
 CD được gọi là trục ngắn. |MF − MF | = 2a 
 ’ ’
 - Đường kính liên hiệp. O, điểm giữa của FF , đặt OF = OF = 
 Hai đường kính của elip gọi là hai c. 
 đường kính liên hiệp nếu mọi dây cung song - Nếu lấy O làm gốc tọa độ như hình 
 song với kính này thì bị đường kính kia chia vẽ, ta có phương trình của hypebol là: 
 X2 Y2
 − = 1 với a2 = c2 - b2. 
 đôi. a2 b2
 Trục dài AB và trục ngắn CD là hai Trục X F, F’ gọi là trục tiêu điểm 
 đường kính liên hiệp đặc biệt, vuông thực của hypebol. 
 góc nhau. Hai đường thẳng ứng với hai phương 
 b b
 1.2. Parabol (Hình.2) trình Y = X và Y = − X là hai đường 
 a a
 tiệm cận của hypebol. 
 Y 
 d 
 Y M Y 
 C M H 
 M 
 F 
 A F O F’ B x O x F F’ x 
 O 
 D 
 H.1 H.2 H.3 
 21 
09/2019 KỶ YẾU HOẠT ĐỘNG KHOA HỌC & GIÁO DỤC TRƯỜNG ĐH KIẾN TRÚC ĐÀ NẴNG 
2. Định lý DANDELIN 1- Rõ ràng rằng, giao tuyến của mặt 
 Cho mặt nón bậc 2 (elip hoặc tròn phẳng với mặt bậc 2 là đường bậc 2. 
xoay) Giao tuyến là elip, parabol, hypebol tùy 
 - Nếu mặt phẳng cắt tất cả đường sinh theo số điểm vô tận của giao tuyến là không, 
của mặt nón, giao tuyến là elip. Trường hợp một và hai. 
suy biến là đỉnh nón. - Mặt phẳng cắt mặt nón ra ba loại 
 - Nếu mặt phẳng cắt mặt nón và song đường bậc 2 như định lý trên. 
song với một đường sinh, giao tuyến là - Mặt phẳng cắt mặt trụ (eliptic, tròn 
parabol. Trường hợp suy biến là đường sinh xoay) ra elip. 
tiếp xúc, ứng với mặt phẳng tiếp xúc mặt - Mặt phẳng cắt mặt paraboloit (eliptic, 
nón. Đường sinh nói trên cho hướng trục tròn xoay) ra elip, parabol. 
của parabol. - Mặt phẳng cắt mặt hypeboloit một 
 - Nếu mặt phẳng cắt mặt nón và song tầng ra ba loại đường bậc 2. 
song với hai đường sinh, giao tuyến là - Mặt phẳng cắt mặt paraboloit 
hypebol. Trường hợp suy biến là hai đường hypeboloit ra parabol, hypebol. 
sinh. Hai đường sinh nói trên cho hướng - Mặt phẳng cắt mặt elipxoloit cho elip. 
tiệm cận của hypebol. Hình 4: sơ đồ minh họa giao tuyến 
 Elip, parabol, hypebol đều có mặt trên phẳng trên mặt nón. 
mặt nón, nên chúng thường được gọi là Hình 5: sơ đồ minh họa giao tuyến 
 ba đường conic. phẳng trên mặt paraboloit hypeboloic. (mặt 
3. Sự có mặt của ba đường conic phẳng P vuông góc với mặt phẳng hình 
 Trong hình học họa hình, chúng chiếu đứng) 
thường có mặt trong các trường hợp sau: 
 S2 
 S2 
 Hypebol P’2 
 P2 P2 
 Parabol 
 Parabol 
 P’2 P2 
 a/ b/ H.5 
 H.4 Hypebol 
 2- Nói chung giao tuyến của hai mặt xứng chung song song với mặt phẳng hình 
bậc 2 là đường cong ghềnh bậc 4. Nếu hai chiếu đứng là hypebol. 
mặt có mặt phẳng đối xứng chung thì hình Hình 7: hình chiếu đứng g2 của giao 
chiếu của giao tuyến lên mặt phẳng đối tuyến mặt nón và mặt cầu có mặt phẳng 
xứng đó là đường bậc 2. đối xứng chung song song với mặt phẳng 
 Hình 6: hình chiếu đứng g2 của giao hình chiếu đứng là parabol. 
tuyến mặt nón và mặt trụ có mặt phẳng đối 
 22 
KỶ YẾU HOẠT ĐỘNG KHOA HỌC & GIÁO DỤC TRƯỜNG ĐH KIẾN TRÚC ĐÀ NẴNG 09/2019 
 S2
 S2 
 g2 
 O2 
 g2 
 H.6 
 H.7 
 3- Trường hợp đặc biệt, giao tuyến bậc Định lý 2: Nếu hai mặt bậc 2 đã tiếp 
 4 của hai mặt bậc 2 nói trên đuôi tách ra xúc nhau ở hai điểm và các mặt phẳng tiếp 
 thành hai đường bậc 2 nếu chúng thỏa mãn xúc chung tại hai điểm đó không trùng nhau 
 các định lý 1, 2, 3 về giao tuyến suy biến thì hai mặt bậc 2 sẽ giao nhau theo hai 
 của hai mặt bậc 2 (trong giáo trình hình học đường bậc 2 đi qua hai điểm tiếp xúc đó. 
 họa hình). Định lý 3: Nếu hai mặt bậc 2 cùng nội 
 Định lý 1: Nếu hai mặt bậc 2 đã cắt tiếp hai cùng ngoại tiếp một mặt bậc 2 thứ 3 
 nhau theo một đường bậc 2 thì chúng còn thì hai mặt bậc 2 sẽ giao nhau theo hai 
 cắt nhau theo một đường bậc 2 nữa. đường bậc 2 đi qua hai giao điểm của hai 
 đường tiếp xúc. 
 S’2 
 S2 
 S2 
 e’2 
 e2
 e2 e2
 c2 
 A2B2 
 p2 O2 
 B1 
 c1 S1 c1 S1 S’1 
 H.8 H.9 H.10 
 A1 
 Hình 8. Giao tuyến của mặt trụ và mặt Hình 9. Giao tuyến của hai mặt trụ là 
 nón là đường tròn c và elip e. hai elip e, e’ đi qua hai tiếp điểm A, B. 
 23 
09/2019 KỶ YẾU HOẠT ĐỘNG KHOA HỌC & GIÁO DỤC TRƯỜNG ĐH KIẾN TRÚC ĐÀ NẴNG 
 Hình 10: giao tuyến của hai mặt nón có 4.3. Định lý Pascal 
mặt cầu nội tiếp chung là elip e và parabol p Nếu một lục giác nội tiếp trong một 
đi qua hai giao điểm của hai đường tròn tiếp đường bậc 2 thì ba cặp cạnh đối diện sẽ 
xúc. giao nhau theo ba điểm thẳng hàng. 
4. Đường bậc 2 trong hình học xạ ảnh, 4.4. Định lý Desargues 2 
aphin Một đường cong bậc 2 biến thiên trong 
 4.1. Cách xác định một đường cong một chùm đường cong bậc 2 thì vạch lên 
bậc 2 trên bất cứ đường thẳng nào hai hàng điểm 
 Định lý: Cho hai chùm liên hệ xạ ảnh liên hệ xạ ảnh đối hợp với nhau. 
sao cho đường nối hai tâm O,O’ không tự 4.5. Nếu đường cong bậc 2 có tâm 
ứng. thì tâm đó là cực của đường thẳng vô tận 
 Quỹ đạo các giao điểm của các tia Elip và hypebol có tâm. Parabol không 
tương ứng là một đường cong bậc 2 đi qua có tâm. 
O, O’. 4.6. Hai đường kính liên hợp đi qua 
 Tiếp tuyến của đường bậc 2 đó tại O, cực của nhau 
O’ là các tia tương ứng với đường Hai đường kính liên hợp chia điều hòa 
 thẳng O, O’. hai tiệm cận. 
 4.2. Hình học aphin là nhóm con 4.7. Vài bài toán giải trí 
của hình học xạ ảnh mà hình tuyệt đối là a/ Bài toán 1: (Hình.11) Cho parabol 
đường thẳng với hai tiếp tuyến PA, PB ( A, B: hai tiếp 
 Trong hình học aphin, ta kéo đường điểm), IA = IB. Chứng minh PI song song 
thẳng vô tận thành đường thẳng thường d∞ với trục của parabol. 
để nghiên cứu các đường bậc 2. Giải: Ta có liên hệ xạ ảnh đối lập (1’, 2 
 Đường bậc 2 tổng quát được biểu diễn ’, ...) và (1, 2, ) với điểm kép 3 ≡ 3’. 
dưới dạng đường trái xoan. Trên đường thẳng vô tận d∞ có hai 
 - Elip là đường bậc 2 không cắt đường điểm kép 1∞ và 3∞. 
thẳng vô tận d∞, không có điểm vô tận nào. Chùm P (ABI∞) điều hòa mà IA = IB 
 - Parabol là đường bậc 2 tiếp với nên PI đi qua 1∞ tức là PI song song với 
đường thẳng vô tận: có một điểm vô tận. trục của parabol. 
 - Hypebol là đường bậc 2 cắt đường b/ Bài toán 2: (Hình.12) Cho giây AB 
thẳng vô tận tại hai điểm: có hai điểm vô của đường bậc 2 với IA = IB. Vẽ giây CID 
tận. và EIF. Đường CE vắt AB ở P, đường DF 
 Các tiếp tuyến tại các điểm vô tận là cắt AB ở Q. Chứng minh IP = IQ. 
các tiệm cận. Giải: AB cắt đường bậc 2 (C) và các 
 Do đó elip có tiệm cận ảo (liên hợp). cạnh tứ điểm ECDF cách các điểm cùng một 
 Parabol có hai tiệm cận trùng với liên hệ xạ ảnh đối hợp: (A,B), (P,Q) (I ≡ I), I 
đường thẳng vô tận. là điểm kép, nên (ABIJ) =(PQIJ) = -1, mà 
 Hypebol có hai tiệm cận IA = IB nên J chạy ra vô tận thành J∞. Vậy 
 IP = IQ. 
 24 
KỶ YẾU HOẠT ĐỘNG KHOA HỌC & GIÁO DỤC TRƯỜNG ĐH KIẾN TRÚC ĐÀ NẴNG 09/2019 
 1∞ 
 d C 
 S∞ E 
 (p) P 
 2’ 1’ B 
 1 2 d 
 33’ A 
 F 
 A I 
 Q D 
 B (e) 
 H.12 
 P 
 H.11 
 S O 
 O D 
 C 
 S 
 K T 
 d∞ 
 I∞ 
 C A I B D (h) 
 (h) 
 A 
 H.13 H.14 
 c/ Bài toán 3: (Hình.13) Cho một AS x CT = B 
 hypebol với hai tiệm cận t và t’. Vẽ một cát AT x CS = D 
 tuyến bất kỳ cắt hypebol tại A, B và cắt hai SO x TO = O 
 tiệm cận tại C1D. Chứng minh AB và CD có Nên BOD là đường Pascal. 
 chung trung điểm. - Có thể dùng định lý Desargues. (Hình 
 Giải: Theo định lý Desargues thì các 14) 
 cặp điểm A, B và C, D xác định một liên hệ Cặp điểm AC trên đường thẳng AC 
 đối hợp nhận điểm vô tận trên cát tuyến là liên hệ đối hợp, nhận điểm K làm điểm kép 
 một điểm kép. Vậy điểm kép thứ hai và trên đường thẳng vô tận. 
 điểm vô tận đó chia điều hòa cả A, B và C, Các điểm B, D, O là các điểm liên hợp 
 D nên điểm kép thứ hai đó là của K nên cùng thuộc đường đối cực của K 
 trung điểm chung của hai đoạn AB và đối với hypebol 
 CD. 5. Lời bàn 
 d/ Bài toán 4: (Hình.14) Chứng minh: Nội dung về đường cong bậc 2 theo 
 Nếu một hình bình hành có hai đỉnh đối diện khái niệm thông thường là vừa sức đối với 
 thuộc hypebol và có các cạnh song song với học sinh, sinh viên trong các trường phổ 
 hai tiệm cận thì hai đỉnh đối diện còn lại thông và kỹ thuật. 
 thẳng hàng với tâm hypebol. 
 Theo định lý Pascal: 
 25 
09/2019 KỶ YẾU HOẠT ĐỘNG KHOA HỌC & GIÁO DỤC TRƯỜNG ĐH KIẾN TRÚC ĐÀ NẴNG 
 Hình học xạ ảnh nghiên cứu đường - Trong khoa học vũ trụ, vệ tinh bay 
cong bậc 2 bao quát hơn, sâu sắc hơn và có quanh quả đất theo quỹ đạo elip với tốc độ 
nhiều bài toán hay. vũ trụ cấp 1, con tàu vũ trụ bay theo quỹ đạo 
 Rất nhiều hình ảnh đường cong bậc 2 parabol với tốc độ cấp 2, bay theo quỹ 
có từ trong trang sách học sinh sinh viên, đạo hypebol với tốc độ cấp 3 
trong đời sống hằng ngày, trong kỹ thuật 6. Kết luận: Các đường conic là một nội 
đến không gian vũ trụ: dung nhỏ của toán học, nhưng đó là một 
 - Các miệng cống xiên, đầu ống tháo khái niệm cơ bản với lý thuyết và bài tập rất 
nước, các nút nối ống, bóng của mái nhà lên phong phú. Các giáo viên nên đầu tư cách 
các cột tròn có dạng elip. dạy sao cho các môn học có liên quan đạt 
 - Các mặt cắt mặt nước thấm qua đập hiệu quả tối ưu. 
đất, mặt cắt chảo rađa có dạng parabol. 
 - Các đầu bút chì 6 cạnh, đầu êcru, TÀI LIỆU THAM KHẢO 
bóng của chao đèn lên tường có dạng [1]. Nguyễn Tư Đôn (2013) Hình học họa 
hypebol. hình 1, NXB Giáo dục Hà Nội. 
 - Hình học Galileé phẳng biểu diễn [2]. Nguyễn Đình Điện, Đỗ Mạnh Môn 
“đường tròn” bằng parabol. (2007) Hình học họa hình 1, NXB Giáo 
 - Hình học Minkovski phẳng biểu diễn dục Hà Nội. 
“đường tròn” bằng hypebol. [3]. Nguyễn Cảnh Toàn (1961) Hình học xạ 
 ảnh, NXB Giáo dục Hà Nội. 
 26