Đề tài Quá trình biên soạn đề kiểm tra 1 tiết trong chủ đề hàm số luỹ thừa, hàm số mũ, hàm số logarit

 TRƯỜNG ĐẠI HỌC SƯ PHẠM- ĐẠI HỌC HUẾ 
 KHOA TOÁN HỌC 
 &œ 
 TRỊNH HOÀNG QUANG LINH 
 QUÁ TRÌNH BIÊN SOẠN ĐỀ KIỂM TRA 1 TIẾT 
TRONG CHỦ ĐỀ HÀM SỐ LUỸ THỪA, HÀM SỐ MŨ, 
 HÀM SỐ LOGARIT 
 HỌC PHẦN: ĐÁNH GIÁ KẾT QUẢ GIÁO DỤC HỌC SINH 
 GVHD: NGUYỄN ĐĂNG MINH PHÚC 
 Huế, 12/2018 
 Lời nói đầu 
 Trong quá trình dạy học, việc kiểm tra đánh giá có vai trò đặc biệt 
quan trọng ảnh hưởng đến toàn bộ quá trình dạy học . Công tác kiểm tra đánh 
giá đang là một đòi hỏi cấp thiết và có ý nghĩa quan trọng đối với việc nâng 
cao chất lượng dạy học nói chung và dạy học môn Toán nói riêng. Nếu kiểm 
tra 15 phút đầu giờ giúp giáo viên nắm bắt được kiến thức và vận dụng kiến 
thức của học sinh trong một tiết học thì thông qua bài kiểm tra 45 phút giáo 
viên sẽ đánh giá được đầy đủ kết quả lĩnh hội kiến thức và có những biện 
pháp điều chỉnh phương pháp phù hợp để đạt hiệu quả cao hơn. 
 Ở bài tiểu luận này, tôi sẽ tìm hiểu về cách thức ra đề kiểm tra 45 
phút cho học sinh lớp 12 chương Hàm số luỹ thừa, hàm số mũ, hàm số 
logarit nhằm giúp cho giáo viên kiểm tra đánh giá học sinh một cách khách 
quan nhất. 
 Với những cố gắng tìm tòi, học hỏi của bản thân để hoàn thành 
bài soạn đề kiểm tra một cách đầy đủ và hoàn chỉnh nhất, song không tránh 
những hạn chế, tôi mong thầy và các bạn góp ý thêm để bài được hoàn chỉnh 
nhất. Tôi cũng cảm ơn chân thành thầy Nguyễn Đăng Minh Phúc đã hướng 
dẫn trong suốt quá trình thực hiện bài soạn. 
Xin chân thành cảm ơn! 
 Sinh viên thực hiện 
 Linh 
 Trinh Hoàng Quang Linh 
 MỤC LỤC 
Lời nói đầu 
I. Xác định mục đích, yêu cầu để kiểm tra .................................................. 1 
II. Mục tiêu chương trình Toán 12 chương hàm số luỹ thừa, hàm số mũ, 
hàm số logarit ................................................................................................... 1 
III. Mức độ nhận thức toán 12 chương hàm số luỹ thừa, hàm số mũ, hàm số 
logarit (chương trình cơ bản) ............................................................................ 3 
IV. Bảng đặc trưng ........................................................................................ 4 
V. Mô tả nội dung bài kiểm tra ..................................................................... 5 
VI. Đề kiểm tra .............................................................................................. 6 
VII. Đáp án và thang điểm .............................................................................. 9 
Tài liệu tham khảo 
I. Xác định mục đích, yêu cầu để kiểm tra 
 Để kiểm tra mức độ tiếp thu kiến thức và năng lực tư duy của học sinh 
 lớp 12 sau khi học xong chương Hàm số luỹ thừa, hàm số mũ, hàm 
 số logarit, giáo viên cần cho học sinh tiến hành thực hiện bài kiểm tra 1 
 tiết với mục đích và yêu cầu như sau: 
 - Kiểm tra được mức độ hiểu biết của học sinh lớp 12 đối với chương 
 hàm số luỹ thừa, hàm số mũ, hàm số logarit. Cách vận dụng linh 
 hoạt nội dung kiến thức của chương, áp dụng các công thức để giải 
 các bài toán liên quan đến thực tế và các bài toán của bộ môn khác 
 có vận dụng kiến thức của chương. 
 - Đề kiểm tra phải có sự phân hoá rõ rệt để giáo viên có thể đưa ra các 
 phương pháp, kế hoạch giảng dạy phù hợp nhằm nâng cao chất 
 lượng học tập của học sinh như: chú ý, kèm cặp các học sinh yếu và 
 tạo cơ hội phát triển tư duy các học sinh giỏi. Mặt khác, đề kiểm tra 
 phải được tổng hợp đầy đủ kiến thức, kĩ năng trong chương. 
 - Đánh giá được quá trình học tập của các em học sinh. 
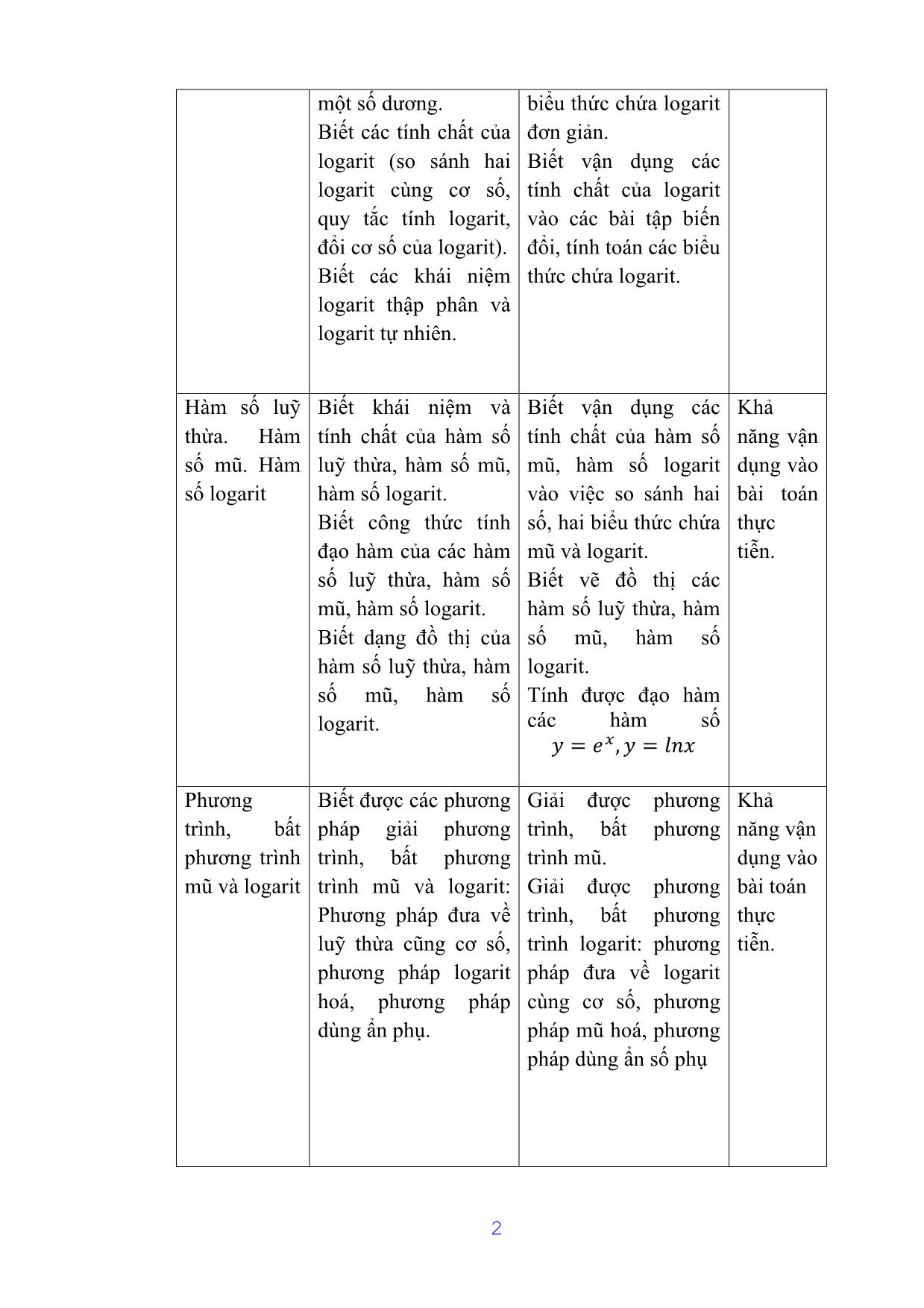
II. Mục tiêu chương trình Toán 12 chương hàm số luỹ thừa, 
 hàm số mũ, hàm số logarit 
 Mục tiêu chương trình Toán 12 chương hàm số luỹ thừa, hàm số mũ, 
 hàm số logarit (chương trình cơ bản). 
 Chủ đề Kiến thức Kĩ năng Thái độ 
 Luỹ thừa Biết các khái niệm Biết dùng các tính Rèn 
 luỹ thừa với số mũ chất của luỹ thừa để luyện 
 nguyên của số thực, đơn giản biểu thức, tính 
 luỹ thừa với số mũ so sánh những biểu chính 
 hữu tỉ và luỹ thừa với thức có chứa luỹ xác, cẩn 
 số mũ thực của số thừa. thận. 
 dương. 
 Biết các tính chất của 
 luỹ thừa với số mũ 
 nguyên, hữu tỉ và 
 thực. 
 Lôgarit Biết khái niệm lôgarit Biết vận dụng định 
 cơ số a (a>0 a≠1) của nghĩa để tính một số 
 1 
 một số dương. biểu thức chứa logarit 
 Biết các tính chất của đơn giản. 
 logarit (so sánh hai Biết vận dụng các 
 logarit cùng cơ số, tính chất của logarit 
 quy tắc tính logarit, vào các bài tập biến 
 đổi cơ số của logarit). đổi, tính toán các biểu 
 Biết các khái niệm thức chứa logarit. 
 logarit thập phân và 
 logarit tự nhiên. 
Hàm số luỹ Biết khái niệm và Biết vận dụng các Khả 
thừa. Hàm tính chất của hàm số tính chất của hàm số năng vận 
số mũ. Hàm luỹ thừa, hàm số mũ, mũ, hàm số logarit dụng vào 
số logarit hàm số logarit. vào việc so sánh hai bài toán 
 Biết công thức tính số, hai biểu thức chứa thực 
 đạo hàm của các hàm mũ và logarit. tiễn. 
 số luỹ thừa, hàm số Biết vẽ đồ thị các 
 mũ, hàm số logarit. hàm số luỹ thừa, hàm 
 Biết dạng đồ thị của số mũ, hàm số 
 hàm số luỹ thừa, hàm logarit. 
 số mũ, hàm số Tính được đạo hàm 
 logarit. các hàm số 
 � = �, � = ��� 
Phương Biết được các phương Giải được phương Khả 
trình, bất pháp giải phương trình, bất phương năng vận 
phương trình trình, bất phương trình mũ. dụng vào 
mũ và logarit trình mũ và logarit: Giải được phương bài toán 
 Phương pháp đưa về trình, bất phương thực 
 luỹ thừa cũng cơ số, trình logarit: phương tiễn. 
 phương pháp logarit pháp đưa về logarit 
 hoá, phương pháp cùng cơ số, phương 
 dùng ẩn phụ. pháp mũ hoá, phương 
 pháp dùng ẩn số phụ 
 2 
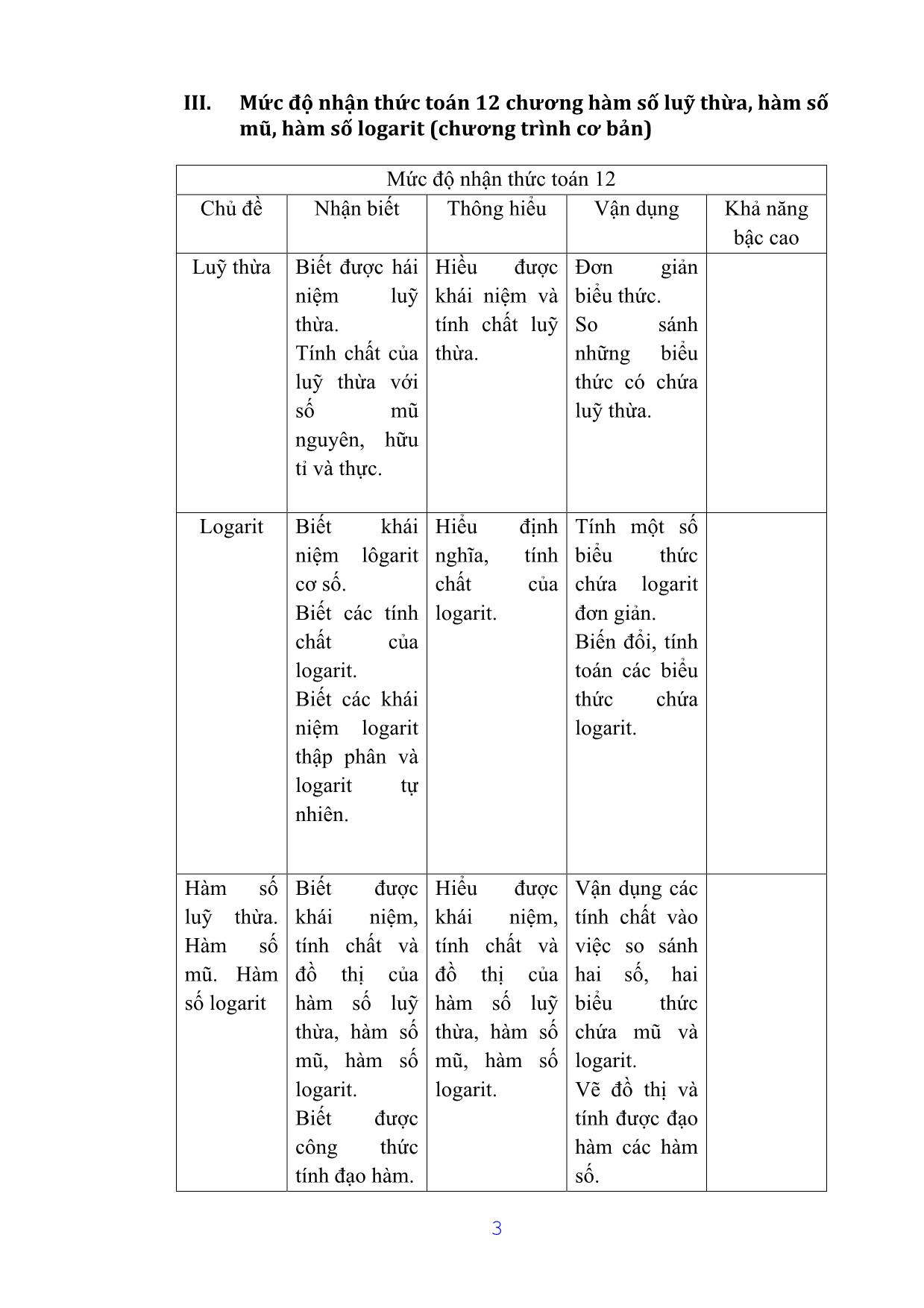
III. Mức độ nhận thức toán 12 chương hàm số luỹ thừa, hàm số 
 mũ, hàm số logarit (chương trình cơ bản) 
 Mức độ nhận thức toán 12 
 Chủ đề Nhận biết Thông hiểu Vận dụng Khả năng 
 bậc cao 
 Luỹ thừa Biết được hái Hiều được Đơn giản 
 niệm luỹ khái niệm và biểu thức. 
 thừa. tính chất luỹ So sánh 
 Tính chất của thừa. những biểu 
 luỹ thừa với thức có chứa 
 số mũ luỹ thừa. 
 nguyên, hữu 
 tỉ và thực. 
 Logarit Biết khái Hiểu định Tính một số 
 niệm lôgarit nghĩa, tính biểu thức 
 cơ số. chất của chứa logarit 
 Biết các tính logarit. đơn giản. 
 chất của Biến đổi, tính 
 logarit. toán các biểu 
 Biết các khái thức chứa 
 niệm logarit logarit. 
 thập phân và 
 logarit tự 
 nhiên. 
Hàm số Biết được Hiểu được Vận dụng các 
luỹ thừa. khái niệm, khái niệm, tính chất vào 
Hàm số tính chất và tính chất và việc so sánh 
mũ. Hàm đồ thị của đồ thị của hai số, hai 
số logarit hàm số luỹ hàm số luỹ biểu thức 
 thừa, hàm số thừa, hàm số chứa mũ và 
 mũ, hàm số mũ, hàm số logarit. 
 logarit. logarit. Vẽ đồ thị và 
 Biết được tính được đạo 
 công thức hàm các hàm 
 tính đạo hàm. số. 
 3 
Phương Biết được các Hiểu được Giải phương Giải các 
trình, bất phương pháp các phương trình, bất bài toán 
phương giải phương pháp giải phương trình thực tế 
trình mũ trình, bất phương trình, mũ và logarit bằng cách 
và logarit phương trình bất phương bằng nhiều đưa về 
 mũ và logarit. trình mũ và phương pháp dạng 
 Phương pháp logarit. khác nhau. phương 
 đưa về luỹ trình, bất 
 thừa cũng cơ phương 
 số, phương trình mũ và 
 pháp logarit logarit. 
 hoá, phương 
 pháp dùng ẩn 
 phụ. 
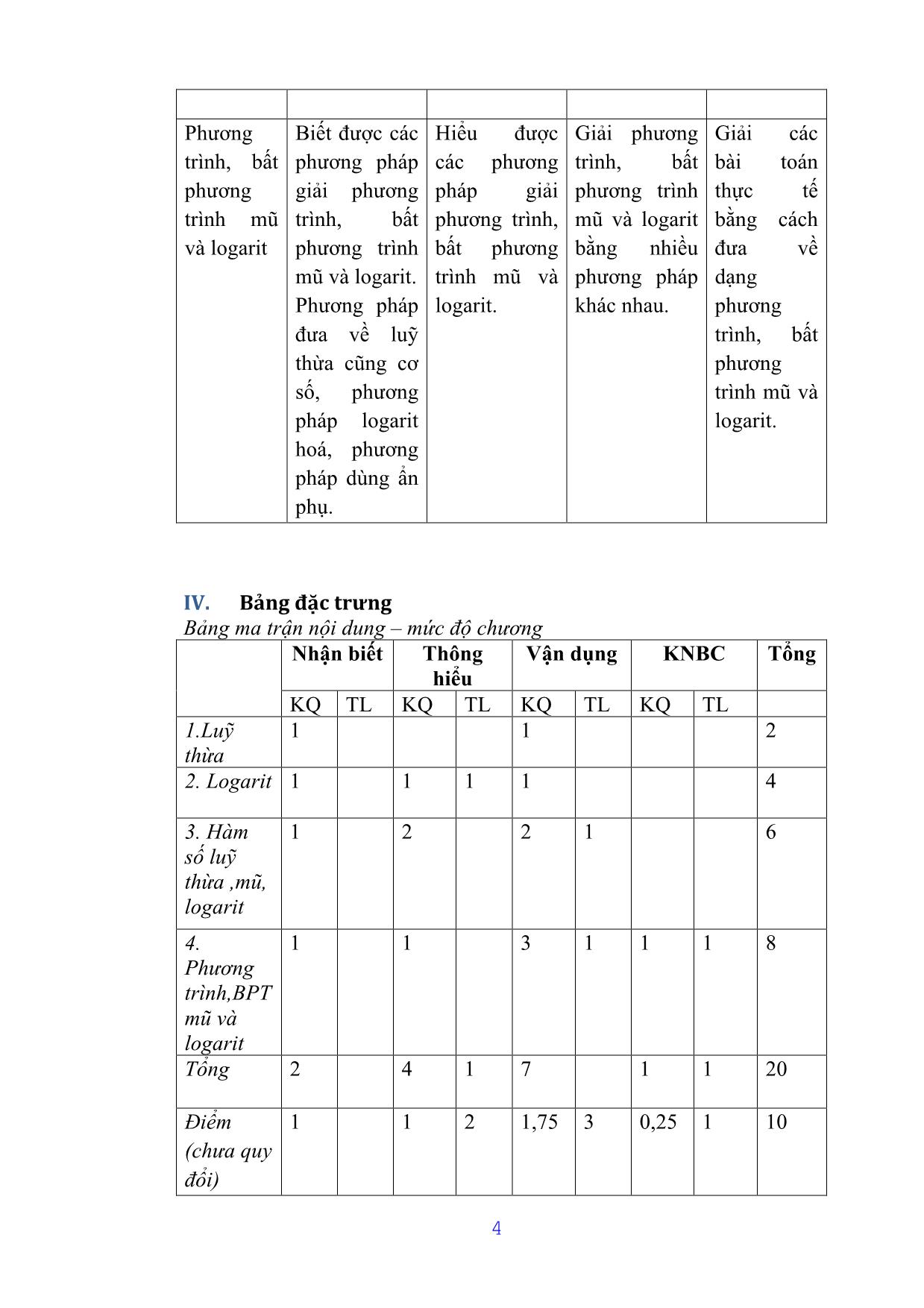
IV. Bảng đặc trưng 
Bảng ma trận nội dung – mức độ chương 
 Nhận biết Thông Vận dụng KNBC Tổng 
 hiểu 
 KQ TL KQ TL KQ TL KQ TL 
1.Luỹ 1 1 2 
thừa 
2. Logarit 1 1 1 1 4 
3. Hàm 1 2 2 1 6 
số luỹ 
thừa ,mũ, 
logarit 
4. 1 1 3 1 1 1 8 
Phương 
trình,BPT 
mũ và 
logarit 
Tổng 2 4 1 7 1 1 20 
Điểm 1 1 2 1,75 3 0,25 1 10 
(chưa quy 
đổi) 
 4 
V. Mô tả nội dung bài kiểm tra 
 Chủ đề 
 @ Luỹ thừa, logarit. 
 @ Hàm số luỹ thừa, hàm số mũ, hàm số logarit. 
 @ Phương trình, bất phương trình mũ và logarit. 
 Mức độ nhận thức 
 ü Trắc nghệm 
 • Câu 1: (Nhận biết) Biết tính chất của hàm luỹ thừa . 
 • Câu 2: (Thông hiểu) Xác định tập xác định của hàm số mũ. 
 • Câu 3: (Vận dụng) Giải bài toán thực tế bằng phương trình mũ. 
 • Câu 4: (Vận dụng) Tìm đạo hàm của hàm mũ. 
 • Câu 5: (Nhận biết) Biết tính chất logarit. 
 • Câu 6: (Vận dụng) Giải phương trình mũ. 
 • Câu 7: (Thông hiểu) Vận dụng đồ thị của hàm số mũ. 
 • Câu 8: (Nhận biết) Nhận biết tính chất của hàm số mũ. 
 • Câu 9: (Thông hiểu) Hiểu tính chất của logarit 
 • Câu 10: (Vận dụng) Giải bài toán bằng cách vận dụng tính chất 
 luỹ thừa. 
 • Câu 11: (Thông hiểu) Tính chất của logarit. 
 • Câu 12: (Vận dụng) Tính đạo hàm của hàm logarit. 
 • Câu 13: (Vận dụng cao) Tìm điều kiện m thoả mãn điều kiện cho 
 trước. 
 • Câu 14: (Nhận biết) Nhận biết tính chất của hàm logarit. 
 • Câu 15: (Vận dụng) Giải bất phương trình logarit. 
 • Câu 16: (Thông hiểu) Tính chất, đồ thị của hàm logarit. 
 ü Tự luận 
 Câu 1: (Nhận biết) Rút gọn biểu thức 
 Câu 2 
 a) (Thông hiểu) Áp dụng công thức để giải bài toán. 
 b) (Thông hiểu) Giải bất phương trình mũ. 
 Câu 3: (Vận dụng) Tính đạo hàm 
 Câu 4: (Vận dụng cao) Giải được bài toán thực tế đưa về việc thiết lập 
 và giải phương trình mũ. 
 5 
 VI. Đề kiểm tra 
KIỂM TRA 45 PHÚT 
Đại số 12, Ban KHTN, Chương hàm số luỹ thừa, hàm số mũ, hàm số logarit 
Phần I: Trắc nghiệm khách quan (4 điểm) 
Câu 1: Mệnh đề nào sau đây sai 
 b > b
 A. a = a. a B.  ⇔ m > n 
 b > 1
 C.√a = |a| D. a. b = (ab) 
Câu 2: Tập xác định của hàm số y = ((−x + 1)(1 − x)) 
 A. D= [−1; +∞) ∖ {±1} B. D= (−1; 1) 
 C. D= (−∞; −1) ∪ (1 + ∞) D. D= (−∞; −1) 
Câu 3: Anh Toàn rất thích lái Grab nên quyết định mua trả góp chiếc 
Lamborghini với giá 300 triệu đồng theo hình thức trả góp. Anh Toàn muốn 
trả trong vòng 2 năm với lãi suất 0.6%. Hỏi hàng tháng anh Toàn phải trả cố 
định số tiền bao nhiêu? 
 A. 12,88 triệu đồng C. 13,46 triệu đồng 
 B. 14,09 triệu đồng D. 14,45 triệu đồng 
 
Câu 4: Đạo hàm của hàm số: � = (−� + 2) là: 
  
     
 A. � =  C. � =  
 () ()
  
     
 B. � =  D. � =  
 ()  ()
Câu 5: Cho a, b, c > 0 và a ∈ (0; 1). Chọn mệnh đề đúng 
 
 A. log b = log b C. log b < log c ⇔ b < c 
     
 
 B. logb a D. log b = αlog� 
Câu 6: Phương trình 25 − 4. 5 + 3 = 0 có nghiệm là: 
 A. x = 0 & x = log5 C. x = 0 & x = log3 
 B. x = 1 & x = 3 D. x = 0 & x = −log3 
 6 
Câu 7: Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số y = a, 
 y = b, y = c được cho trong hình vẽ bên. Mệnh đề nào dưới đây là đúng? 
 A. a < b < c C. c < a < b 
 B. b < c < a D. a < c < b 
Câu 8: Hàm số nào dưới đây đồng biến trên tập xác định của nó? 
    
 A. y =   B. y = π C. y = (0,2) D. y =   
  
  
Câu 9: Giá trị của a √ (a > 0, a ≠ 1) là 
 
 A. √7 B. 49 C. D.7 
 
Câu 10: Tính giá trị của biểu thức: P = (7 + 4√3)(4√3 − 7) 
 A. P = 1 B. P = 7 − 4√3 
 C. P = 7 + 4√3 D. . P = (7 + 4√3) 
Câu 11: Đặt = log3 . Tính theo a giá trị của biểu thức log1125 
    
 A. 1 + B.2 + C. 2 + D. 1 + 
    
Câu 12: Cho hàm số f(x) = ln(x + √x + 1). Giá trị f′(1) là: 
    
 A. √ B. C. √ D. 1 + √ 
  √  
Câu 13: Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 
16 − 2. 12 + (m − 2)9 = 0 có nghiệm dương? 
 A. 1 B. 2 C. 4 D. 3 
Câu 14: Xét phương trình a > b (1). Mệnh đề nào sau đây sai? 
 A. Nếu 0 0 thì S = (−∞; loga). 
 B. Nếu a > 1, b ≤ 0 thì S = ℝ. 
 C. Nếu 0 < a < 1, b ≤ 0 thì S = ℝ. 
 D. Nếu a > 1, b > 0 thì S = (logb; +∞). 
 7 
Câu 15: Tập nghiệm của bất phương trình log(x − 1) + log(11 − 2x) ≥ 0 
 
là: 
 
 A. S = (1; 4] B. S = (−∞; 4] C. S = 3;  D. S = (1; 4) 
 
Câu 16: Cho hàm số y = x −ln(x + 1). Khẳng định nào sau đây đúng? 
 A. Hàm có tập xác định là ℝ ∖ {−1}. 
 B. Hàm số nghịch biến trên (-1;0). 
 C. Hàm số đồng biến trên (−∞; 0) 
 D. Hàm số đồng biến trên (−1; +∞) 
Phần II: Tự luận (6 điểm) 
Câu 1 (2 điểm) Tính giá trị của biểu thức sau: A = 4 + 3 
Câu 2 (2 điểm) Giải phương trình và bất phương trình sau: 
 a. logx + log(x − 1) = 1 
 
  ( )
 b. 5   < 1 
Câu 3 (1 điểm) Cho hàm số f(x) = ln√1 + �. Tính f’(ln2) 
Câu 4 (1 điểm) Anh Nam muốn xây nhà, chi phí dự kiến 1 tỷ đồng . Hiện nay 
anh Nam có 700 triệu. Vì không muốn vay tiền nên Nam quyết định gửi số 
tiền 700 triệu vào ngân hàng với lãi suất 12%/1 năm, tiền lãi của năm trước 
được cộng vào tiền gốc của năm sau. Tuy nhiên giá xây dựng cũng tăng 1% 
so với năm trước. Hỏi sau bao lâu anh Nam sẽ tiết kiệm đủ tiền để xây nhà.? 
 8 
 VII. Đáp án và thang điểm 
Trắc nghiệm (gồm 16 câu, mỗi câu 0,25 điểm) 
Câu hỏi 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 
Đáp án C A B C B C D B B C A C B A A B 
Tự luận 
 Câu Nội dung Điểm 
 log 6 2+log 2
Câu 1 Tính A = 4 2 + 3 3 
(2 điểm) 1 điểm 
 = 2log26 + 3. 3 
 0,5 điểm 
 = 2log236 + 9.2 
 0,5 điểm 
 A = 36 + 18 = 54 
Câu 2 a. ĐK: x > 1 0,25 điểm 
(2 điểm) 
 logx + log(x − 1) = log[x(x − 1)] = 1 = log2 0,25 điểm 
 ⇔ x(x − 1) = 2 ⇔ x − x − 2 = 0 0,25 điểm 
 ⇔ x = −1 hoặc x = 2 
 Kết hợp điều kiện chọn x = 2. Vậy S = {2} 
 
 b. ĐK > 0 ⇔ x 2 0,25 điểm 
 
  0,25 điểm 
 Bpt ⇔ log   < 0 = log 1 
   
   0,25 điểm 
 ⇔ 0 ⇔ x > 0 
  
 Kết hợp điều kiện suy ra S = (2; +∞) 0,25 điểm 
Câu 3 (√e + 1) e 0,5 điểm 
 f (x) = = 
  
(1 điểm) √e + 1 2(e + 1) 
 e 2 1
 f (ln2) = = = 0,5 điểm 
 2(e + 1) 6 3
 9 
 Gọi V là tổng số tiền vật liệu sau n năm, T là tổng số 
 tiền thu được sau n năm. 
Câu 4 
 Ta có: V = 1 ( tỉ ) Suy ra V = 1(1 + 1%) ( tỉ ) 
(1 điểm)   0,25 điểm 
 Số tiền thu được sau n năm là T = 0,7. (1 + 12%) 
  
 Để xây được nhà thì ở năm thứ n thì số tiền anh thu 
 được phải bằng số tiền vật liệu. Suy ra 
   
 T = V ⇔ 0,7. (1 + 12%) = 1(1 + 1%) 
 0,5 điểm 
 1 + 12%  1 1
 ⇔   = ⇔ n = log% ≈ 3,5 
 1 + 1% 0,7 % 0,7 
 ≈ 3 năm 6 tháng 0,25 điểm 
 10 
 Tài liệu tham khảo 
1. Đánh giá trong giáo dục toán - Nguyễn Đăng Minh Phúc – Đại học sư 
 phạm Huế 
2. Sách giáo khoa đại số (cơ bản) lớp 12 – Bộ giáo dục và đào tạo 
3. Tiếp cận phương pháp và vận dụng cao trong trắc nghiệm bài toán thực 
 tế - Trần Công Diêu, Nguyễn Văn Quang 
4. https://toanmath.com/2018/10/phan-dang-va-bai-tap-trac-nghiem-luy-
 thua-mu-va-logarit-co-dap-an-nguyen-bao-vuong.html 
5. https://toanmath.com/2017/11/100-bai-toan-trac-nghiem-ham-so-mu-
 ham-so-logarit-co-dap-an-phung-hoang-em.html 
 11