Đề cương chi tiết học phần Đại số tuyến tính

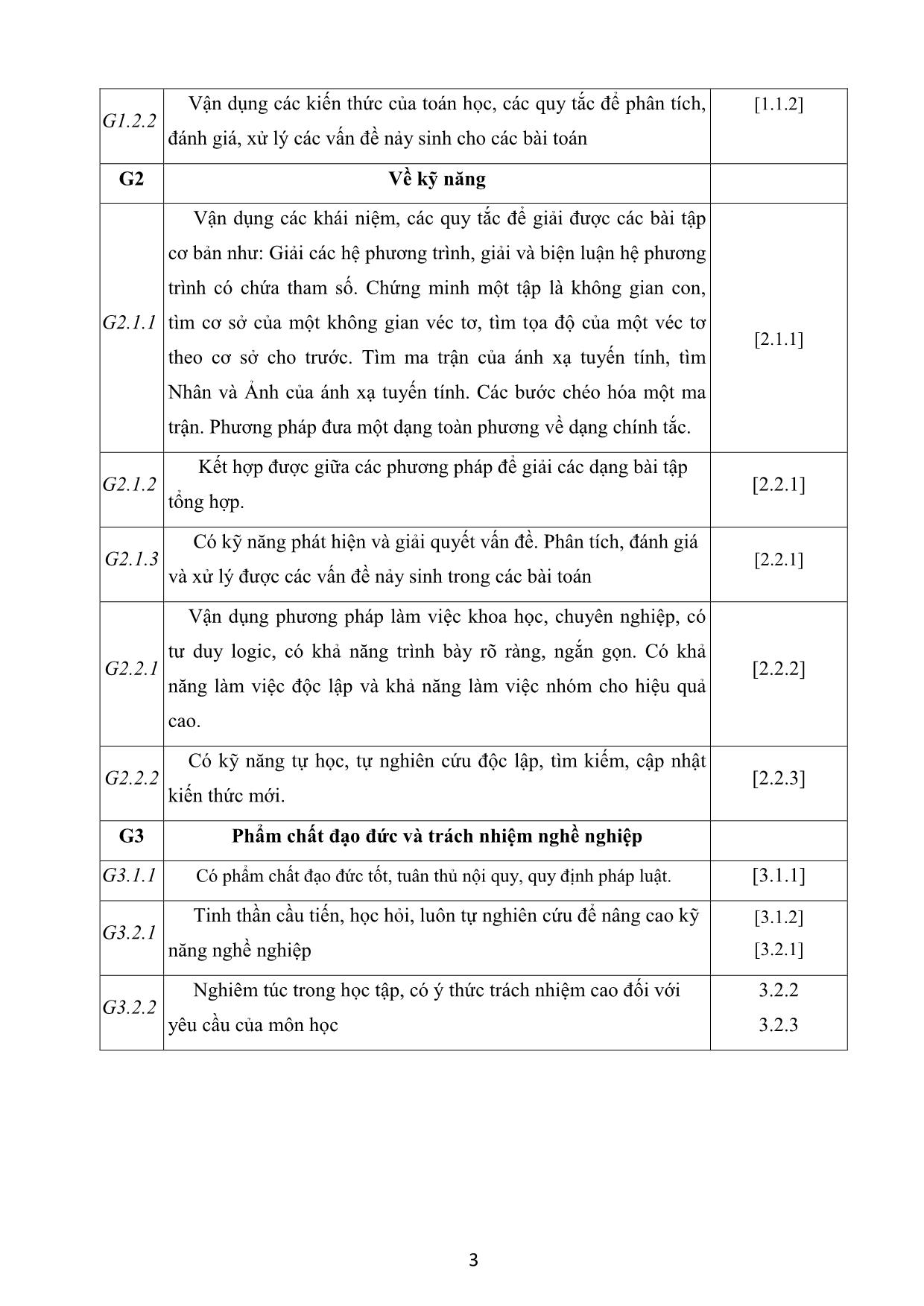
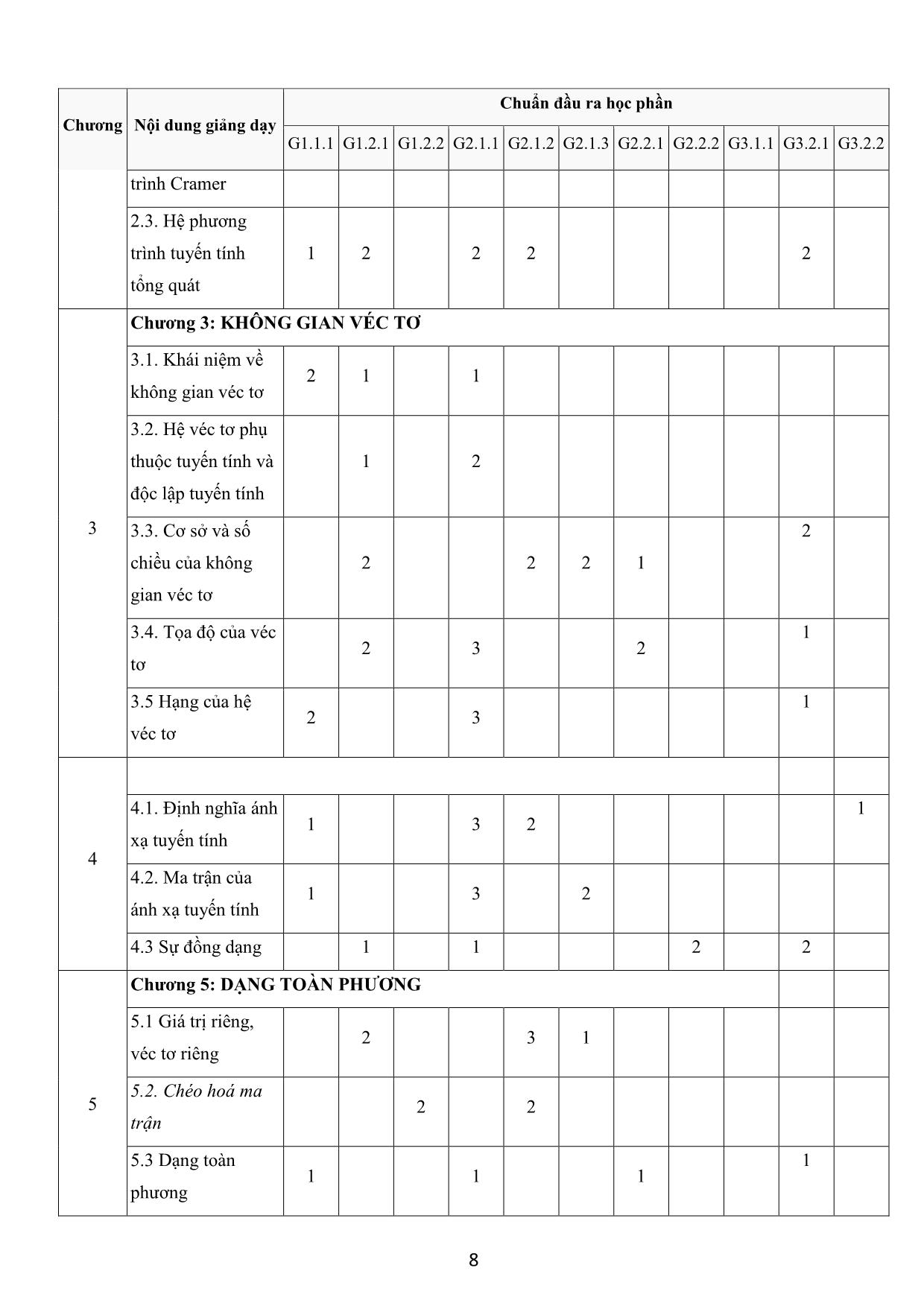
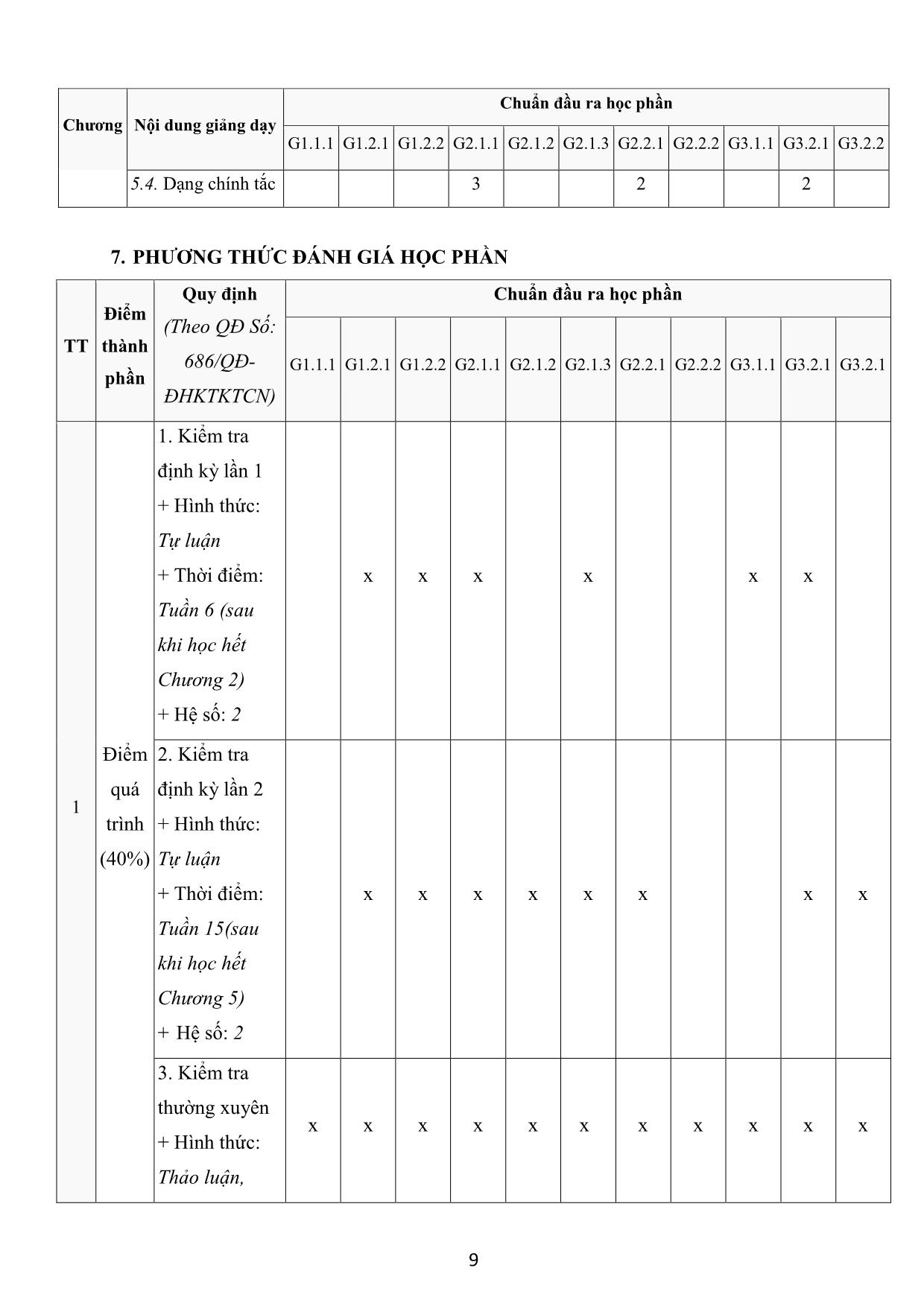
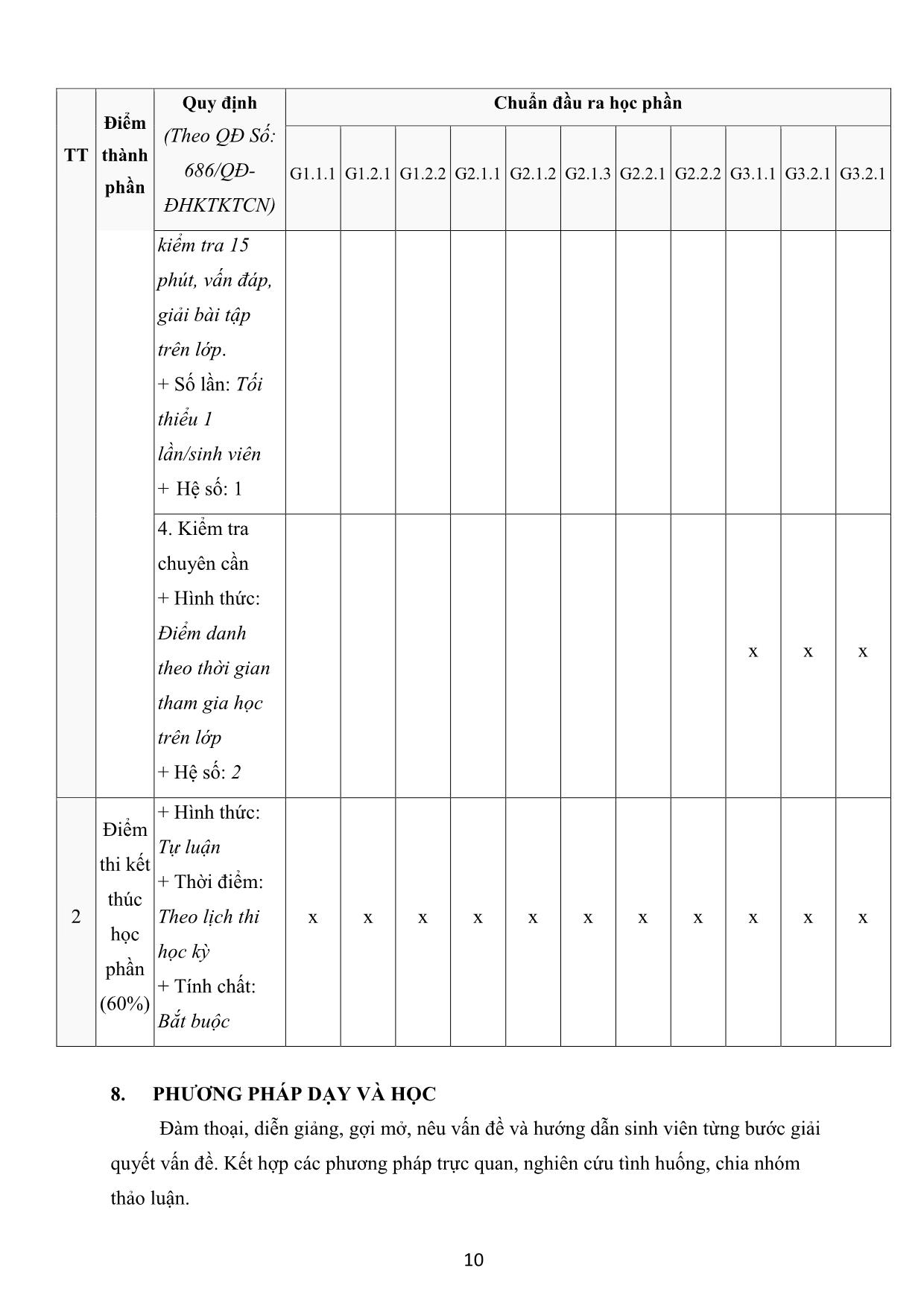
 TRƯỜNG ĐẠI HỌC KINH TẾ KỸ THUẬT CÔNG NGHIỆP 
 KHOA KHOA HỌC CƠ BẢN 
 BỘ: MÔN TOÁN 
 ĐỀ CƯƠNG CHI TIẾT 
 HỌC PHẦN: ĐẠI SỐ TUYẾN TÍNH 
1. THÔNG TIN CHUNG 
 Tên học phần (tiếng Việt): ĐẠI SỐ TUYẾN TÍNH 
 Tên học phần (tiếng Anh): LINEAR ALGEBRA 
 Mã môn học: 12 
 Khoa/Bộ môn phụ trách: Bộ môn Toán – Khoa Khoa học Cơ bản 
 Giảng viên phụ trách chính: Phạm Văn Bằng 
 Email:pvbang@uneti.edu.vn 
 Phòng làm việc: 
 Giảng viên tham gia giảng dạy: TS.Phạm Văn Bằng, TS. Lê Xuân Huy, Lê Thanh 
 Sơn, ThS. Cao Thị Thanh Xuân, ThS. Lê Lệ Hằng, 
 ThS. Hà Thị Thanh, ThS. Trần Văn Toàn, ThS. Vũ 
 Thị Ngọc. 
 Số tín chỉ: 2(26,8,60) 
 Số tiết Lý thuyết: 26 tiết 
 Số tiết TH/TL trên lớp: 8 tiết 
 26+8/2 = 15 tuần x 2 tiết/tuần 
 Số tiết Tự học: 60 giờ 
 - Tính chất của học phần: Bắt buộc 
 - Điều kiện tham dự học phần: 
 Học phần tiên quyết: Không 
 Học phần học trước: Không 
 Các yêu cầu của học phần: Sinh viên có tài liệu học tập 
 1 
 2. MÔ TẢ HỌC PHẦN 
 Đại số tuyến tính là một trong những học phần bắt buộc của kiến thức giáo dục đại 
 cương theo khung chương trình đào tạo. Học phần này nhằm trang bị cho sinh viên 
 những kiến thức cơ sở về toán học làm nền tảng cho các môn học chuyên ngành về sau. 
 Nội dung học phần được chia thành 5 chương với 2 tín chỉ (Chương 1: Ma trận và định 
 thức; Chương 2: Hệ phương trình tuyến tính; Chương 3: Không gian véc tơ; Chương 4: 
 Ánh xạ tuyến tính; Chương 5: Giá trị riêng, véc tơ riêng và dạng toàn phương). 
 3. MỤC TIÊU CỦA HỌC PHẦN ĐỐI VỚI NGƯỜI HỌC 
 Kiến thức 
 Trang bị cho sinh viên những kiến thức cơ bản về Đại số tuyến tính như ma trận, 
 hệ phương trình, không gian véc tơ, ánh xạ tuyến tính, chéo hóa một ma trận và 
 dạng toàn phương. Từ đó có thể tự hoàn thiện, phát triển, vận dụng và giải quyết 
 những vấn đề liên quan trong các môn học chuyên nghành sau này. 
 Kỹ năng 
 Rèn luyện cho sinh viên khả năng tư duy có logic, có phương pháp phân tích, 
 tổng hợp và giải quyết các bài toán một cách khoa học, có khả năng làm việc nhóm. 
 Năng lực tự chủ và trách nhiệm 
 Nghiêm túc, trách nhiệm, chủ động, tích cực, chăm chỉ, có khả năng tự học hỏi, tự 
 nghiên cứu. 
 4. CHUẨN ĐẦU RA HỌC PHẦN 
 Mã Mô tả CĐR học phần CĐR của 
 CĐR Sau khi học xong môn học này, người học có thể: CTĐT 
 G1 Về kiến thức 
 Trình bày được các khài niệm cơ bản của đại số tuyến tính như: 
 [1.1.1] 
G1.1.1 Ma trận, định thức, hệ phương trình tuyến tính, không gian véc tơ, 
 ánh xạ tuyến tính, chéo hóa ma trận và dạng toàn phương. 
 Nắm vững các kiến thức cơ bản về: Biến đổi sơ cấp đối với ma 
 trận, các dạng hệ phương trình, cơ sở của không gian véc tơ, hạng 
 [1.1.2] 
G1.2.1 của hệ véc tơ, Nhân và Ảnh của ánh xạ tuyến tính, ma trận của 
 ánh xạ tuyến tính, điều kiện để chéo hóa một ma trận, dạng toàn 
 [1.2.1] 
 phương và dạng chính tắc của nó. 
 2 
 Vận dụng các kiến thức của toán học, các quy tắc để phân tích, [1.1.2] 
G1.2.2 
 đánh giá, xử lý các vấn đề nảy sinh cho các bài toán 
 G2 Về kỹ năng 
 Vận dụng các khái niệm, các quy tắc để giải được các bài tập 
 cơ bản như: Giải các hệ phương trình, giải và biện luận hệ phương 
 trình có chứa tham số. Chứng minh một tập là không gian con, 
G2.1.1 tìm cơ sở của một không gian véc tơ, tìm tọa độ của một véc tơ 
 [2.1.1] 
 theo cơ sở cho trước. Tìm ma trận của ánh xạ tuyến tính, tìm 
 Nhân và Ảnh của ánh xạ tuyến tính. Các bước chéo hóa một ma 
 trận. Phương pháp đưa một dạng toàn phương về dạng chính tắc. 
 Kết hợp được giữa các phương pháp để giải các dạng bài tập 
G2.1.2 [2.2.1] 
 tổng hợp. 
 Có kỹ năng phát hiện và giải quyết vấn đề. Phân tích, đánh giá 
 G2.1.3 [2.2.1] 
 và xử lý được các vấn đề nảy sinh trong các bài toán 
 Vận dụng phương pháp làm việc khoa học, chuyên nghiệp, có 
 tư duy logic, có khả năng trình bày rõ ràng, ngắn gọn. Có khả 
 G2.2.1 [2.2.2] 
 năng làm việc độc lập và khả năng làm việc nhóm cho hiệu quả 
 cao. 
 Có kỹ năng tự học, tự nghiên cứu độc lập, tìm kiếm, cập nhật 
 G2.2.2 [2.2.3] 
 kiến thức mới. 
 G3 Phẩm chất đạo đức và trách nhiệm nghề nghiệp 
G3.1.1 Có phẩm chất đạo đức tốt, tuân thủ nội quy, quy định pháp luật. [3.1.1] 
 Tinh thần cầu tiến, học hỏi, luôn tự nghiên cứu để nâng cao kỹ [3.1.2] 
G3.2.1 
 năng nghề nghiệp [3.2.1] 
 Nghiêm túc trong học tập, có ý thức trách nhiệm cao đối với 3.2.2 
G3.2.2 
 yêu cầu của môn học 3.2.3 
 3 
5. NỘI DUNG MÔN HỌC, KẾ HOẠCH GIẢNG DẠY 
Tuần Số tiết Số tiết Tài liệu học 
 Nội dung 
 thứ LT TH tập, tham khảo 
 Chương 1. MA TRẬN - ĐỊNH THỨC 
 1.1. Ma trận 
 1.1.1. Các định nghĩa về ma trận 
 1 2 0 1, 2, 3, 4, 5 
 1.1.2. Các phép toán về ma trận 
 1.1.3. Các phép biến đổi sơ cấp. Ma trận 
 bậc thang 
 1.2. Định thức 
 1.2.1. Định nghĩa về định thức 
 2 2 0 1, 2, 3, 4, 5 
 1.2.2. Các tính chất của định thức 
 1.2.3. Các phương pháp tính định thức 
 1.3. Ma trận nghịch đảo 
 1.3.1. Định nghĩa về ma trận nghịch đảo, điều 
 kiện tồn tại ma trận nghịch đảo. 
 3 1.3.2. Cách tìm ma trận nghịch đảo. 2 0 1, 2, 3, 4, 5 
 1.4. Hạng của ma trận 
 1.4.1. Khái niệm hạng của ma trận 
 1.4.2. Các phương pháp tìm hạng ma trận 
 Chương 2. : HỆ PHƯƠNG TRÌNH TUYẾN 
 TÍNH 
 2.1. Khái niệm về hệ phương trình tuyến tính 
 2.1.1. Dạng tổng quát của hệ phương trình 
 tuyến tính 
 4 2 0 1, 2, 3, 4, 5 
 2.1.2. Dạng ma trận của hệ phương trình tuyến 
 tính 
 2.2. Hệ phương trình Cramer 
 2.2.1. Định nghĩa về hệ phương trình Cramer 
 2.2.2. Phương pháp Cramer 
 4 
Tuần Số tiết Số tiết Tài liệu học 
 Nội dung 
 thứ LT TH tập, tham khảo 
 2.2.3. Phương pháp Gauss 
 2.3. Hệ phương trình tuyến tính tổng quát 
 5 1, 2, 3, 4, 5 
 2.3.1. Điều kiện tồn tại nghiệm 2 0 
 2.3.2 Hệ phương trình tuyến tính thuần nhất 
 6 Chữa bài tập + Kiểm tra 0 4 1, 2, 3, 4, 5 
 Chương 3: KHÔNG GIAN VÉC TƠ 
 3.1. Khái niệm về không gian véc tơ 
 3.1.1. Định nghĩa không gian véc tơ 
 3.1.2. Các tính chất của không gian véc tơ 
 3.1.3 Không gian con 
 3.2. Hệ véc tơ phụ thuộc tuyến tính và độc lập 
 7 2 0 1, 2, 3, 4, 5 
 tuyến tính 
 3.2.1. Tổ hợp tuyến tính 
 3.2.2. Sự phụ thuộc tuyến tính và độc lập tuyến 
 tính của một hệ véc tơ 
 3.2.3. Các định lý cơ bản về sự phụ thuộc tuyến 
 tính 
 3.3. Cơ sở và số chiều của không gian véc tơ 
 3.3.1. Định nghĩa về hệ sinh và cơ sở 
 3.3.2 Không gian hữu hạn chiều 
 3.3.3. Cơ sở của một không gian véc tơ 
 8 2 0 1, 2, 3, 4, 5 
 3.4. Tọa độ của véc tơ 
 3.4.1. Tọa độ của một véc tơ đối với một cơ sở 
 3.4.2. Ma trận chuyển cơ sở. Công thức biến 
 đổi tọa độ 
 3.5 Hạng của hệ véc tơ 
 9 3.5.1 Định nghĩa hạng của một hệ véc tơ 2 0 1, 2, 3, 4, 5 
 3.5.2 Các định lý cơ bản về hạng của hệ véc tơ 
 5 
Tuần Số tiết Số tiết Tài liệu học 
 Nội dung 
 thứ LT TH tập, tham khảo 
 3.5.3 Cách tính hạng và cơ sở của không gian 
 sinh bởi một hệ véc tơ 
 Chương 4: ÁNH XẠ TUYẾN TÍNH 
 4.1. Định nghĩa 
 10 4.1.1. Định nghĩa ánh xạ tuyến tính 2 0 1, 2, 3, 4, 5 
 4.1.2. Nhân và ảnh của ánh xạ tuyến tính 
 4.1.3. Hạng của ánh xạ tuyến tính 
 4.2. Ma trận của ánh xạ tuyến tính 
 4.2.1. Định nghĩa ma trận của ánh xạ tuyến 
 tính 
 11 4.3 Sự đồng dạng 2 0 1, 2, 3, 4, 5 
 4.3.1. Ma trận đồng dạng 
 4.3.2. Ma trận của ánh xạ tuyến tính khi 
 chuyển cơ sở 
 Chương 5: DẠNG TOÀN PHƯƠNG 
 5.1 Giá trị riêng, véc tơ riêng 
 5.1.1. Định nghĩa về giá trị riêng, véc tơ riêng 
 của ma trận 
 5.1.2. Phương trình đặc trưng. Cách tìm giá trị 
 12 2 0 1, 2, 3, 4, 5 
 riêng và véc tơ riêng 
 5.2. Chéo hoá ma trận 
 5.2.1. Điều kiện cần và đủ để ma trận vuông 
 chéo hóa được 
 5.2.2. Các phương pháp chéo hóa ma trận 
 5.3 Dạng toàn phương 
 5.3.1. Dạng song tuyến tính và dạng song 
 13 
 tuyến tính đối xứng. 2 0 1, 2, 3, 4, 5 
 5.3.2 Định nghĩa dạng toàn phương 
 6 
 Tuần Số tiết Số tiết Tài liệu học 
 Nội dung 
 thứ LT TH tập, tham khảo 
 5.3.3. Ma trận của dạng toàn phương 
 5.3.5. Hạng của dạng toàn phương 
 5.4. Dạng chính tắc 
 5.4.1. Định nghĩa 
 5.4.2. Đưa dạng toàn phương về dạng chính tắc 
 14 2 0 1, 2, 3, 4, 5 
 bằng phép biến đổi trực giao 
 5.4.3. Đưa dạng toàn phương về dạng chính tắc 
 bằng phương pháp Lagrange 
 15 Chữa bài tập + Kiểm tra 0 4 1, 2, 3, 4, 5 
 6. MA TRẬN MỨC ĐỘ ĐÓNG GÓP CỦA NỘI DUNG GIẢNG DẠY ĐỂ ĐẠT 
 ĐƯỢC CHUẨN ĐẦU RA CỦA HỌC PHẦN 
 Mức 1: Thấp 
 Mức 2: Trung bình 
 Mức 3: Cao 
 Chuẩn đầu ra học phần 
Chương Nội dung giảng dạy 
 G1.1.1 G1.2.1 G1.2.2 G2.1.1 G2.1.2 G2.1.3 G2.2.1 G2.2.2 G3.1.1 G3.2.1 G3.2.2 
 Chương 1. MA TRẬN - ĐỊNH THỨC 
 1.1. Ma trận 3 3 1 2 2 2 
 1.2. Định thức 2 1 2 1 
 1 1.3. Ma trận nghịch 2 
 2 2 2 
 đảo 
 1.4. Hạng của ma 
 2 3 2 
 trận 
 Chương 2. : HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 
 2.1. Khái niệm về 2 
 2 hệ phương trình 2 3 
 tuyến tính 
 2.2. Hệ phương 2 3 2 1 
 7 
 Chuẩn đầu ra học phần 
Chương Nội dung giảng dạy 
 G1.1.1 G1.2.1 G1.2.2 G2.1.1 G2.1.2 G2.1.3 G2.2.1 G2.2.2 G3.1.1 G3.2.1 G3.2.2 
 trình Cramer 
 2.3. Hệ phương 
 trình tuyến tính 1 2 2 2 2 
 tổng quát 
 Chương 3: KHÔNG GIAN VÉC TƠ 
 3.1. Khái niệm về 
 2 1 1 
 không gian véc tơ 
 3.2. Hệ véc tơ phụ 
 thuộc tuyến tính và 1 2 
 độc lập tuyến tính 
 3 3.3. Cơ sở và số 2 
 chiều của không 2 2 2 1 
 gian véc tơ 
 3.4. Tọa độ của véc 1 
 2 3 2 
 tơ 
 3.5 Hạng của hệ 1 
 2 3 
 véc tơ 
 4.1. Định nghĩa ánh 1 
 1 3 2 
 xạ tuyến tính 
 4 
 4.2. Ma trận của 
 1 3 2 
 ánh xạ tuyến tính 
 4.3 Sự đồng dạng 1 1 2 2 
 Chương 5: DẠNG TOÀN PHƯƠNG 
 5.1 Giá trị riêng, 
 2 3 1 
 véc tơ riêng 
 5.2. Chéo hoá ma 
 5 2 2 
 trận 
 5.3 Dạng toàn 1 
 1 1 1 
 phương 
 8 
 Chuẩn đầu ra học phần 
Chương Nội dung giảng dạy 
 G1.1.1 G1.2.1 G1.2.2 G2.1.1 G2.1.2 G2.1.3 G2.2.1 G2.2.2 G3.1.1 G3.2.1 G3.2.2 
 5.4. Dạng chính tắc 3 2 2 
 7. PHƯƠNG THỨC ĐÁNH GIÁ HỌC PHẦN 
 Quy định Chuẩn đầu ra học phần 
 Điểm 
 (Theo QĐ Số: 
TT thành 
 686/QĐ- G1.1.1 G1.2.1 G1.2.2 G2.1.1 G2.1.2 G2.1.3 G2.2.1 G2.2.2 G3.1.1 G3.2.1 G3.2.1 
 phần 
 ĐHKTKTCN) 
 1. Kiểm tra 
 định kỳ lần 1 
 + Hình thức: 
 Tự luận 
 + Thời điểm: x x x x x x 
 Tuần 6 (sau 
 khi học hết 
 Chương 2) 
 + Hệ số: 2 
 Điểm 2. Kiểm tra 
 quá định kỳ lần 2 
1 
 trình + Hình thức: 
 (40%) Tự luận 
 + Thời điểm: x x x x x x x x 
 Tuần 15(sau 
 khi học hết 
 Chương 5) 
 + Hệ số: 2 
 3. Kiểm tra 
 thường xuyên 
 x x x x x x x x x x x 
 + Hình thức: 
 Thảo luận, 
 9 
 Quy định Chuẩn đầu ra học phần 
 Điểm 
 (Theo QĐ Số: 
TT thành 
 686/QĐ- G1.1.1 G1.2.1 G1.2.2 G2.1.1 G2.1.2 G2.1.3 G2.2.1 G2.2.2 G3.1.1 G3.2.1 G3.2.1 
 phần 
 ĐHKTKTCN) 
 kiểm tra 15 
 phút, vấn đáp, 
 giải bài tập 
 trên lớp. 
 + Số lần: Tối 
 thiểu 1 
 lần/sinh viên 
 + Hệ số: 1 
 4. Kiểm tra 
 chuyên cần 
 + Hình thức: 
 Điểm danh 
 x x x 
 theo thời gian 
 tham gia học 
 trên lớp 
 + Hệ số: 2 
 + Hình thức: 
 Điểm 
 Tự luận 
 thi kết 
 + Thời điểm: 
 thúc 
2 Theo lịch thi x x x x x x x x x x x 
 học 
 học kỳ 
 phần 
 + Tính chất: 
 (60%) 
 Bắt buộc 
 8. PHƯƠNG PHÁP DẠY VÀ HỌC 
 Đàm thoại, diễn giảng, gợi mở, nêu vấn đề và hướng dẫn sinh viên từng bước giải 
 quyết vấn đề. Kết hợp các phương pháp trực quan, nghiên cứu tình huống, chia nhóm 
 thảo luận. 
 10 
 Sinh viên tập trung nghiên cứu lý thuyết, áp dụng lý thuyết bài tập. Hoàn thành tốt 
các bài tập thảo luận và nhiệm vụ của giảng viên giao. 
 Trong quá trình học tập, sinh viên được khuyến khích đặt câu hỏi phản biện, trình 
bày quan điểm, các ý tưởng sáng tạo mới dưới nhiều hình thức khác nhau. 
 9. QUY ĐỊNH CỦA HỌC PHẦN 
9.1. Quy định về tham dự lớp học 
 Sinh viên có trách nhiệm tham dự đầy đủ các buổi học. Trong trường hợp nghỉ học 
do lý do bất khả kháng thì phải có giấy tờ chứng minh đầy đủ và hợp lý. 
 Sinh viên nghỉ học từ 50% số tiết trở lên (dù có lý do hay không có lý do) trong 
chương trình sẽ bị cấm thi và phải đăng ký học lại vào học kỳ sau. 
 Tham dự các tiết học lý thuyết. 
 Thực hiện đầy đủ các bài tập được giao. 
 Tham dự kiểm tra định kỳ, thi kết thúc học phần. 
 Chủ động tổ chức thực hiện giờ tự học theo hướng dẫn. 
9.2. Quy định về hành vi lớp học 
 Học phần được thực hiện trên nguyên tắc tôn trọng người học và người dạy. Mọi 
hành vi làm ảnh hưởng đến quá trình dạy và học đều bị nghiêm cấm. 
 Sinh viên phải đi học đúng giờ quy định. Sinh viên đi trễ quá 15 phút sau khi giờ 
học bắt đầu sẽ không được tham dự buổi học. 
 Tuyệt đối không làm ồn, gây ảnh hưởng đến người khác trong quá trình học. 
 Tuyệt đối không được ăn uống, nhai kẹo cao su, sử dụng các thiết bị như điện thoại, 
máy nghe nhạc trong giờ học. 
 Máy tính xách tay, máy tính bảng chỉ được thực hiện vào mục đích ghi chép bài 
giảng, tính toán phục vụ bài giảng, bài tập, tuyệt đối không dùng vào việc khác. 
 Máy tính xách tay, máy tính bảng chỉ được thực hiện vào mục đích ghi chép bài 
giảng, tính toán phục vụ bài giảng, bài tập, tuyệt đối không dùng vào việc khác. 
10. TÀI LIỆU HỌC TẬP, THAM KHẢO 
10.1. Tài liệu học tập: 
[1]. Phạm Văn Bằng, Lê Xuân Huy, Cao Thị Thanh Xuân, Tài liệu học tập Đại số tuyến tính, 
NXB Trường Đại học Kinh tế Kỹ thuật Công nghiệp. 
10.2. Tài liệu tham khảo: 
 11 
[2]. Nguyễn Đình Trí, Tạ Văn Đĩnh, Nguyễn Hồ Quỳnh Toán học cao cấp. Tập 1 : Đại 
số và hình học giải tích Nguyễn Đình Trí, NXB Giáo dục, 2011. 
[3]. Lê Tuấn Hoa, Đại số tuyến tính qua các ví dụ và bài tập, Nhà xuất bản Đại học Quốc 
gia Hà Nội, 2006. 
[4]. Trần Lưu Cường, Nguyễn Đình Huy, Huỳnh Bá Lân, Toán cao cấp 2: Đại số tuyến 
tính, NXB Giáo dục, 2005. 
[5]. David C. Lay, Steven R. Lay, Judi J. McDonald, Linear Algebra and Its 
Applications,NXB Pearson , 2016. 
11. HƯỚNG DẪN THỰC HIỆN 
 Khoa Khoa học Cơ bản và Bộ môn Toán có trách nhiệm phổ biến đề cương chi tiết 
học phần cho toàn thể giáo viên tham gia giảng dạy thực hiện. 
 Giảng viên có nhiệm vụ phổ biến đề cương chi tiết cho sinh viên vào tiết học đầu 
tiên của học phần. 
 Giảng viên thực hiện theo đúng nội dung và kế hoạch giảng dạy trong đề cương chi 
tiết đã được duyệt. 
 Hà nội, ngày tháng năm 2018 
 Trưởng khoa Trưởng bộ môn Người biên soạn 
 (Ký và ghi rõ họ tên) (Ký và ghi rõ họ tên) (Ký và ghi rõ họ tên) 
 12