Đánh giá các thuật toán tối ưu đối với mô hình mạng nơ-ron tích chập trong tác vụ nhận diện hình ảnh

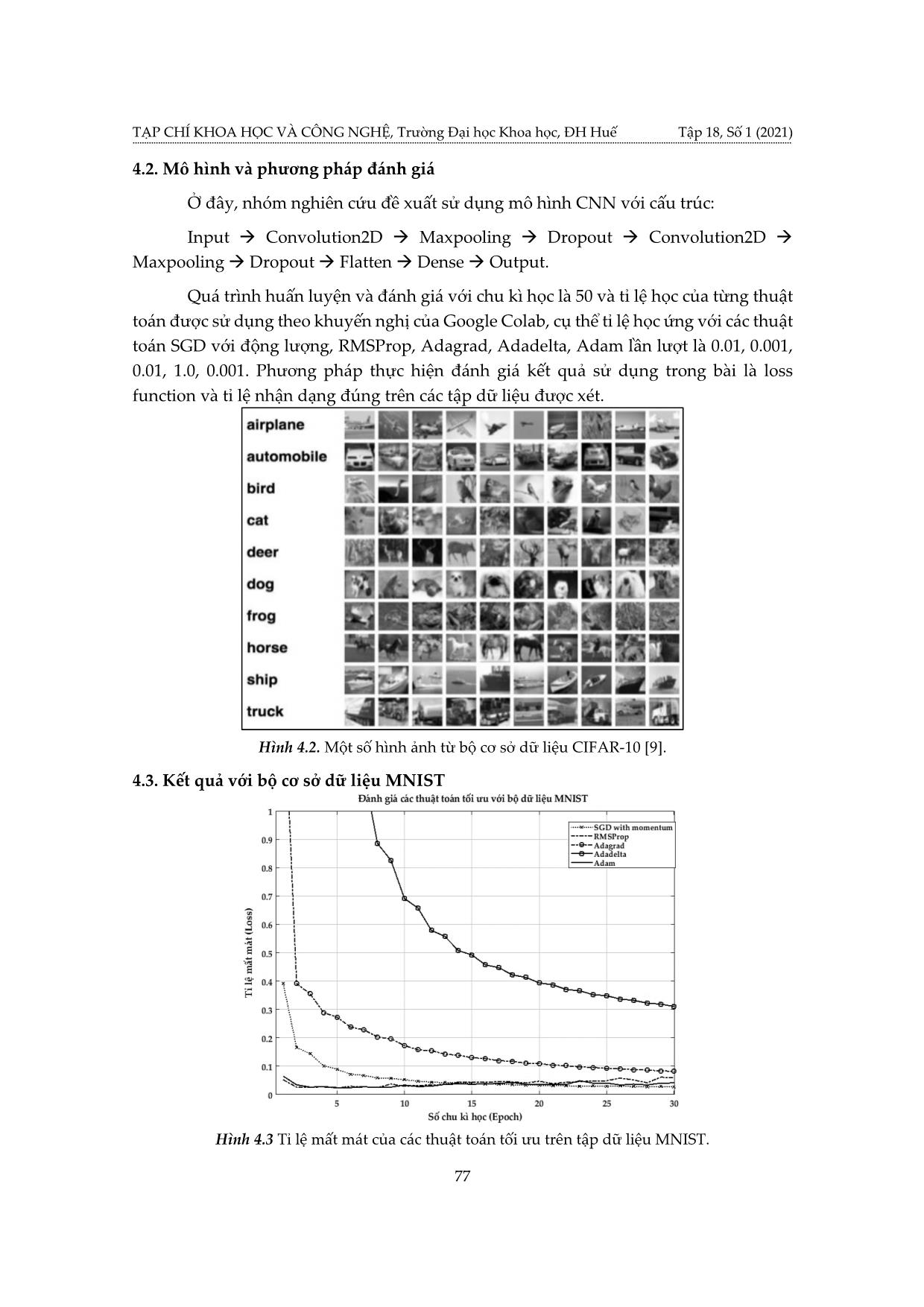
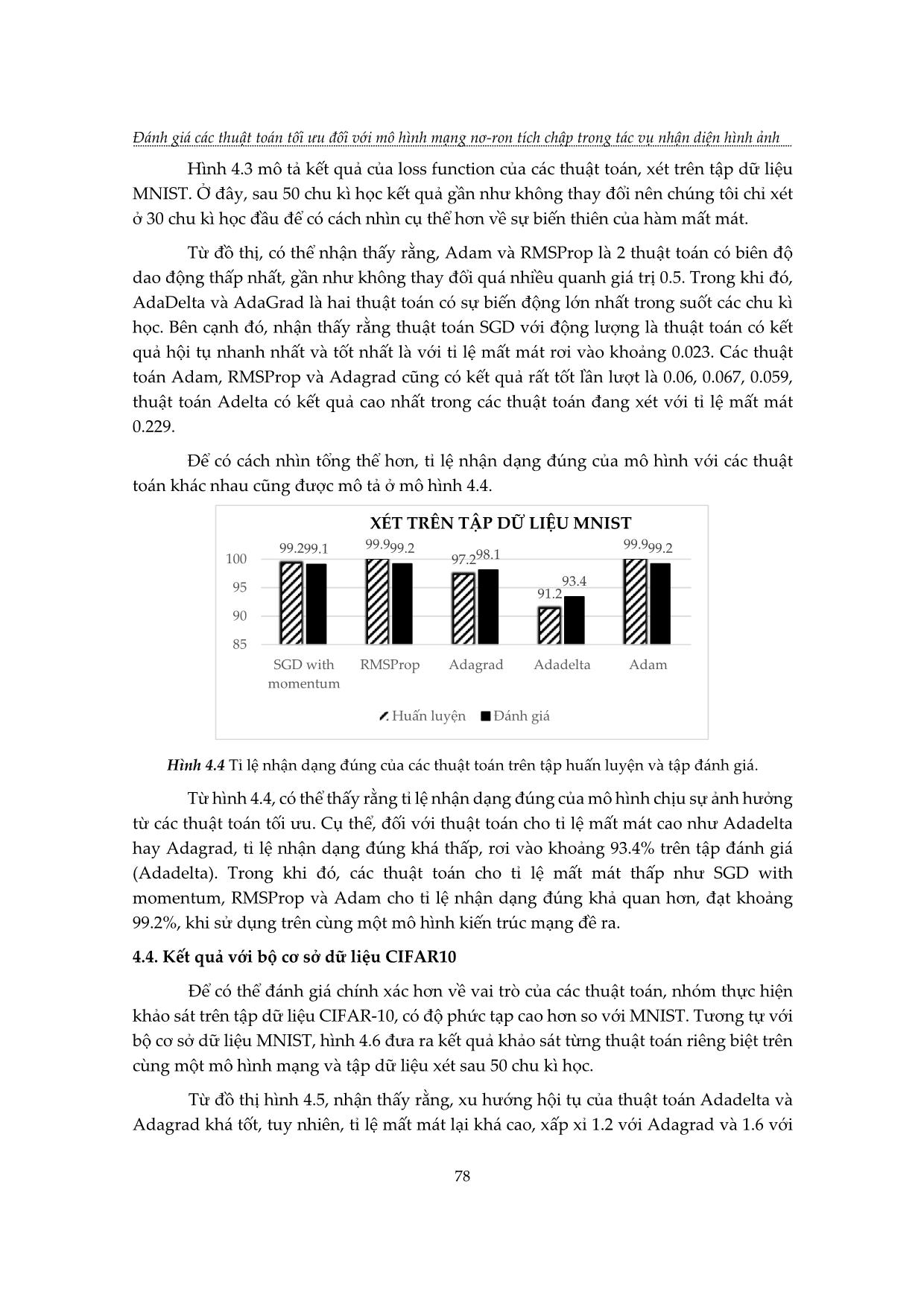
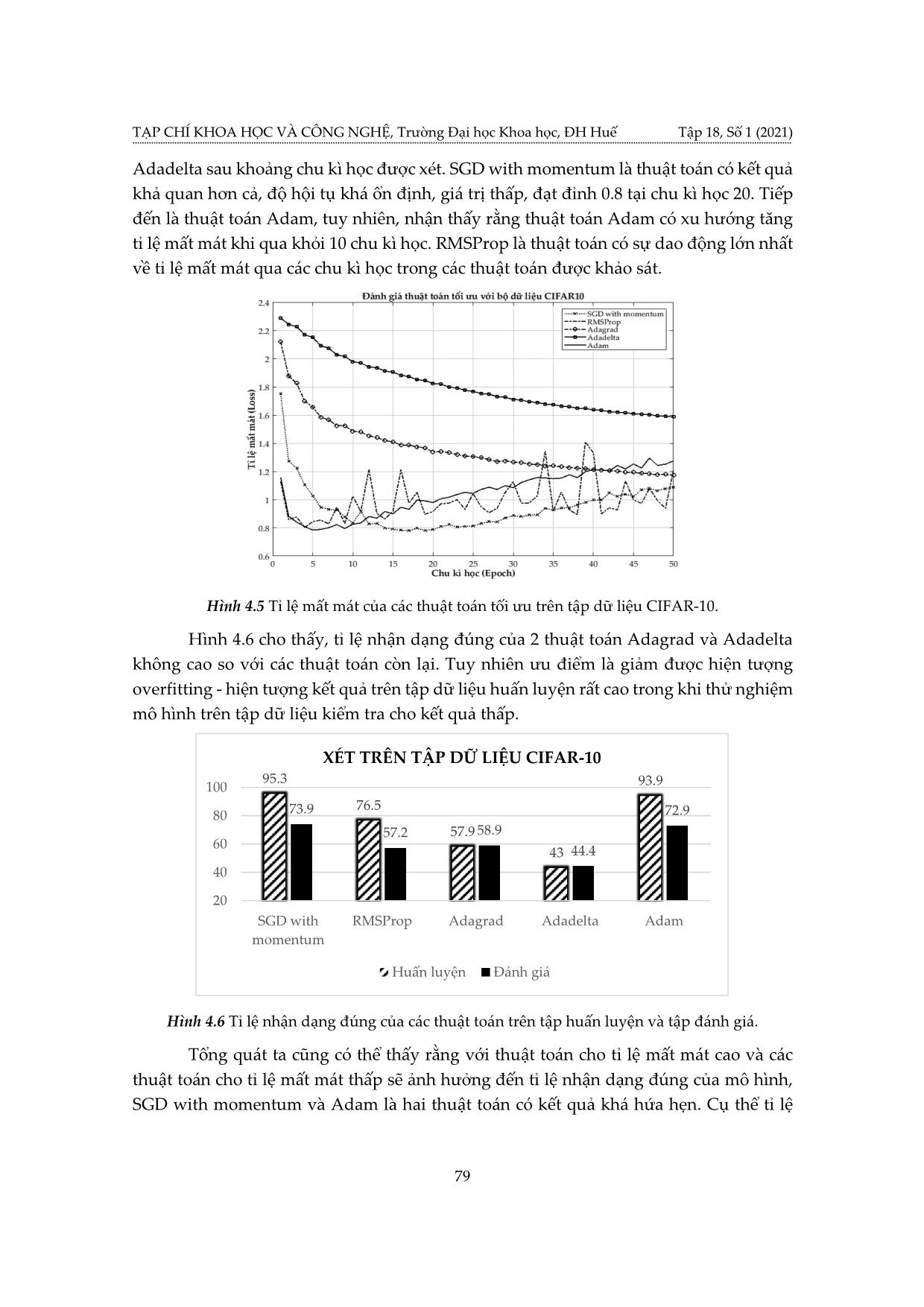
ên các kết quả đó 
có thể đánh giá tác động của thuật toán tối ưu đến mô hình mạng ứng dụng vào bài toán 
nhận dạng hình ảnh. 
3.1. Gradient Descent 
 Gradient Descent (GD) là thuật toán tìm tối ưu chung cho các hàm số. Ý tưởng 
chung của GD là điều chỉnh các tham số để lặp đi lặp lại thông qua mỗi dữ liệu huấn 
luyện để giảm thiểu hàm chi phí. 
 ( +1) ( ) ( )
 푤 = 푤 − 휂 ∇푤 퐽(푤 ) (3.1) 
 Với 푤( ) là tham số tại bước cập nhật tại lớp k, η là tỉ lệ học, 퐽(푤) là hàm 
 ( ) ( )
lỗi, ∇푤 퐽(푤 ): đạo hàm của hàm lỗi tại điểm 푤 . 
3.2. SGD với động lượng (SGD with momentum) 
 SGD với momentum là phương pháp giúp tăng tốc các vectơ độ dốc theo đúng 
hướng, và giúp hệ thống hội tụ nhanh hơn. Đây là một trong những thuật toán tối ưu 
hóa phổ biến nhất và nhiều mô hình hiện đại sử dụng nó để đào tạo. Mô tả như sau: 
 푣푗 ← 훼 ∗ 푣푗 − 휂 ∗ 훻푊 ∑ 퐿 (푤) 
 1 (3.2) 
 푤푗 ← 푣푗 + 푤푗 
 Phương trình (3.2) có hai phần. Thuật ngữ đầu tiên là độ dốc vj được giữ lại từ 
các lần lặp trước. Hệ số động lượng α là tỉ lệ phần trăm của độ dốc được giữ lại mỗi lần 
lặp. L là hàm mất mát, η là tỉ lệ học. 
3.3. RMSProp (Root Mean Square Propogation) 
 RMSProp sử dụng trung bình bình phương của gradient để chuẩn hóa 
gradient. Có tác dụng cân bằng kích thước bước - giảm bước cho độ dốc lớn để tránh 
hiện tượng phát nổ độ dốc (Exploding Gradient), và tăng bước cho độ dốc nhỏ để tránh 
biến mất độ dốc (Vanishing Gradient). RMSProp tự động điều chỉnh tốc độ học tập, và 
chọn một tỉ lệ học tập khác nhau cho mỗi tham số. Phương pháp cập nhật các trọng số 
 74 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 18, Số 1 (2021) 
được thực hiện như mô tả: 
 2
 푠푡 = 휌푠푡−1 + (1 − 휌) ∗ 푡 
 휂
 훥 푡 = − ∗ 푡 (3.3) 
 √푠푡 + 휖
 푡+1 = 푡 + 훥 푡 
 Với 푠푡: tích luỹ phương sai của các gradient trong quá khứ, 휌: tham số suy giảm, 
훥 푡: sự thay đổi các tham số trong mô hình, 푡: gradient của các tham số tại vòng lặp t, 
ϵ: tham số đảm bảo kết quả xấp xỉ có ý nghĩa. 
3.4. Adagrad 
 Adagrad là một kỹ thuật học máy tiên tiến, thực hiện giảm dần độ dốc bằng cách 
thay đổi tốc độ học tập. Adagrad được cải thiện hơn bằng cách cho trọng số học tập 
chính xác dựa vào đầu vào trước nó để tự điều chỉnh tỉ lệ học theo hướng tối ưu nhất 
thay vì với một tỉ lệ học duy nhất cho tất cả các nút. 
 휂
 푤푡+1 = 푤푡 − . 푡 (3.4) 
 √ 푡 + 휖
 Trong công thức (3.4), Gt là ma trận đường chéo chứa bình phương của đạo hàm 
vecto tham số tại vòng lặp t; gt là vectơ của độ dốc cho vị trí hiện tại và η là tỉ lệ học. 
3.5. Adadelta 
 Adadelta là một biến thể khác của AdaGrad. Adadelta không có tham số tỉ lệ học. 
Thay vào đó, nó sử dụng tốc độ thay đổi của chính các tham số để điều chỉnh tỉ lệ học 
nghĩa là bằng cách giới hạn cửa sổ của gradient tích lũy trong quá khứ ở một số kích 
thước cố định của trọng số w. 
 ′ 훥 푡−1 + 휖
 푡 = √ . 푡 
 푠푡 + 휖
 (3.5) 
 ′
 푡 = 푡−1 − 푡 
 2
 훥 푡 = 휌훥 푡−1 + (1 − 휌) 푡 
 Từ công thức (3.5), Adadelta sử dụng 2 biến trạng thái: 푠푡 để lưu trữ trung bình 
của khoảng thời gian thứ hai của gradient và Δ 푡 để lưu trữ trung bình của khoảng thời 
 ′
gian thứ 2 của sự thay đổi các tham số trong mô hình. 푡: căn bậc hai thương của trung 
bình tốc độ thay đổi bình phương và trung bình mô-men bậc hai của gradient. 
3.6. Adam 
 Adam được xem như là sự kết hợp của RMSprop và Stochastic Gradient Descent 
với động lượng. Adam là một phương pháp tỉ lệ học thích ứng, nó tính toán tỉ lệ học tập 
cá nhân cho các tham số khác nhau. Adam sử dụng ước tính của khoảng thời gian thứ 
nhất và thứ hai của độ dốc để điều chỉnh tỉ lệ học cho từng trọng số của mạng nơ-ron. 
 75 
Đánh giá các thuật toán tối ưu đối với mô hình mạng nơ-ron tích chập trong tác vụ nhận diện hình ảnh 
Tuy nhiên, qua nghiên cứu thực nghiệm, trong một số trường hợp, Adam vẫn còn gặp 
phải nhiều thiếu sót so với thuật toán SGD. Thuật toán Adam được mô tả: 
 푡 = 훽1 푡−1 + (1 − 훽1) 푡 
 (3.6) 
 2
 푣푡 = 훽2푣푡−1 + (1 − 훽2) 푡 
 Trong công thức (3.6), vt là trung bình động của bình phương và mt là trung bình 
động của gradient; β1và β2 là tốc độ của di chuyển. 
4. ĐÁNH GIÁ KẾT QUẢ VỚI CÁC THUẬT TOÁN TỐI ƯU 
4.1. Cơ sở dữ liệu 
 Để thực hiện khảo sát và đánh giá các thuật toán tối ưu với bài toán phân loại hình 
ảnh, nhóm nghiên cứu đề xuất hai tập cơ sở dữ liệu phổ biến cho mục đích nghiên cứu 
là MNIST và CIFAR-10 để thực hiện quá trình đào tạo và thực nghiệm. 
4.1.1. MNIST 
 Bộ dữ liệu MNIST là bộ dữ liệu gồm các hình ảnh xám (grayscale picture) các chữ 
số viết tay được chia sẻ bởi Yann Lecun bao gồm 70000 ảnh chữ số viết tay được chia 
thành 2 tập: tập huấn luyện gồm 60000 ảnh và tập kiểm tra 10000 ảnh. Các chữ số viết 
tay ở tập MNIST được chia thành 10 nhóm tương ứng với các chữ số từ 0 đến 9. Tất cả 
hình ảnh trong tập MNIST đều được chuẩn hóa với kích thước 28 x 28 điểm ảnh. Dưới 
đây là một số hình ảnh được trích xuất từ bộ dữ liệu. 
 Hình 4.1. Hình ảnh chữ số viết tay từ tập MNIST [8]. 
4.1.2. CIFAR-10 
 Bộ cơ sở dữ liệu CIFAR10 là bộ dữ liệu chứa các ảnh màu có kích thước 32 x 32 x 
3 (3 lớp màu RGB) trong 10 nhóm khác nhau, gồm: máy bay, ô tô, chim, mèo, hươu, chó, 
ếch, ngựa, tàu và xe tải. Mỗi nhóm gồm 6000 hình ảnh, cùng với sự đa dạng về các thành 
phần như độ sáng, vị trí, hướng của các đối tượng. Nó là một trong những bộ dữ liệu 
được sử dụng rộng rãi nhất cho nghiên cứu máy học bao gồm 60000 ảnh được chia thành 
2 tập: tập huấn luyện gồm 50000 ảnh và tập kiểm tra 10000 ảnh. 
 76 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 18, Số 1 (2021) 
4.2. Mô hình và phương pháp đánh giá 
 Ở đây, nhóm nghiên cứu đề xuất sử dụng mô hình CNN với cấu trúc: 
 Input → Convolution2D → Maxpooling → Dropout → Convolution2D → 
Maxpooling → Dropout → Flatten → Dense → Output. 
 Quá trình huấn luyện và đánh giá với chu kì học là 50 và tỉ lệ học của từng thuật 
toán được sử dụng theo khuyến nghị của Google Colab, cụ thể tỉ lệ học ứng với các thuật 
toán SGD với động lượng, RMSProp, Adagrad, Adadelta, Adam lần lượt là 0.01, 0.001, 
0.01, 1.0, 0.001. Phương pháp thực hiện đánh giá kết quả sử dụng trong bài là loss 
function và tỉ lệ nhận dạng đúng trên các tập dữ liệu được xét. 
 Hình 4.2. Một số hình ảnh từ bộ cơ sở dữ liệu CIFAR-10 [9]. 
4.3. Kết quả với bộ cơ sở dữ liệu MNIST 
 Hình 4.3 Tỉ lệ mất mát của các thuật toán tối ưu trên tập dữ liệu MNIST. 
 77 
Đánh giá các thuật toán tối ưu đối với mô hình mạng nơ-ron tích chập trong tác vụ nhận diện hình ảnh 
 Hình 4.3 mô tả kết quả của loss function của các thuật toán, xét trên tập dữ liệu 
MNIST. Ở đây, sau 50 chu kì học kết quả gần như không thay đổi nên chúng tôi chỉ xét 
ở 30 chu kì học đầu để có cách nhìn cụ thể hơn về sự biến thiên của hàm mất mát. 
 Từ đồ thị, có thể nhận thấy rằng, Adam và RMSProp là 2 thuật toán có biên độ 
dao động thấp nhất, gần như không thay đổi quá nhiều quanh giá trị 0.5. Trong khi đó, 
AdaDelta và AdaGrad là hai thuật toán có sự biến động lớn nhất trong suốt các chu kì 
học. Bên cạnh đó, nhận thấy rằng thuật toán SGD với động lượng là thuật toán có kết 
quả hội tụ nhanh nhất và tốt nhất là với tỉ lệ mất mát rơi vào khoảng 0.023. Các thuật 
toán Adam, RMSProp và Adagrad cũng có kết quả rất tốt lần lượt là 0.06, 0.067, 0.059, 
thuật toán Adelta có kết quả cao nhất trong các thuật toán đang xét với tỉ lệ mất mát 
0.229. 
 Để có cách nhìn tổng thể hơn, tỉ lệ nhận dạng đúng của mô hình với các thuật 
toán khác nhau cũng được mô tả ở mô hình 4.4. 
 XÉT TRÊN TẬP DỮ LIỆU MNIST
 99.299.1 99.999.2 99.999.2
 100 97.298.1
 93.4
 95 91.2
 90
 85
 SGD with RMSProp Adagrad Adadelta Adam
 momentum
 Huấn luyện Đánh giá
 Hình 4.4 Tỉ lệ nhận dạng đúng của các thuật toán trên tập huấn luyện và tập đánh giá. 
 Từ hình 4.4, có thể thấy rằng tỉ lệ nhận dạng đúng của mô hình chịu sự ảnh hưởng 
từ các thuật toán tối ưu. Cụ thể, đối với thuật toán cho tỉ lệ mất mát cao như Adadelta 
hay Adagrad, tỉ lệ nhận dạng đúng khá thấp, rơi vào khoảng 93.4% trên tập đánh giá 
(Adadelta). Trong khi đó, các thuật toán cho tỉ lệ mất mát thấp như SGD with 
momentum, RMSProp và Adam cho tỉ lệ nhận dạng đúng khả quan hơn, đạt khoảng 
99.2%, khi sử dụng trên cùng một mô hình kiến trúc mạng đề ra. 
4.4. Kết quả với bộ cơ sở dữ liệu CIFAR10 
 Để có thể đánh giá chính xác hơn về vai trò của các thuật toán, nhóm thực hiện 
khảo sát trên tập dữ liệu CIFAR-10, có độ phức tạp cao hơn so với MNIST. Tương tự với 
bộ cơ sở dữ liệu MNIST, hình 4.6 đưa ra kết quả khảo sát từng thuật toán riêng biệt trên 
cùng một mô hình mạng và tập dữ liệu xét sau 50 chu kì học. 
 Từ đồ thị hình 4.5, nhận thấy rằng, xu hướng hội tụ của thuật toán Adadelta và 
Adagrad khá tốt, tuy nhiên, tỉ lệ mất mát lại khá cao, xấp xỉ 1.2 với Adagrad và 1.6 với 
 78 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 18, Số 1 (2021) 
Adadelta sau khoảng chu kì học được xét. SGD with momentum là thuật toán có kết quả 
khả quan hơn cả, độ hội tụ khá ổn định, giá trị thấp, đạt đỉnh 0.8 tại chu kì học 20. Tiếp 
đến là thuật toán Adam, tuy nhiên, nhận thấy rằng thuật toán Adam có xu hướng tăng 
tỉ lệ mất mát khi qua khỏi 10 chu kì học. RMSProp là thuật toán có sự dao động lớn nhất 
về tỉ lệ mất mát qua các chu kì học trong các thuật toán được khảo sát. 
 Hình 4.5 Tỉ lệ mất mát của các thuật toán tối ưu trên tập dữ liệu CIFAR-10. 
 Hình 4.6 cho thấy, tỉ lệ nhận dạng đúng của 2 thuật toán Adagrad và Adadelta 
không cao so với các thuật toán còn lại. Tuy nhiên ưu điểm là giảm được hiện tượng 
overfitting - hiện tượng kết quả trên tập dữ liệu huấn luyện rất cao trong khi thử nghiệm 
mô hình trên tập dữ liệu kiểm tra cho kết quả thấp. 
 XÉT TRÊN TẬP DỮ LIỆU CIFAR-10
 95.3
 100 93.9
 76.5
 80 73.9 72.9
 57.2 57.9 58.9
 60
 43 44.4
 40
 20
 SGD with RMSProp Adagrad Adadelta Adam
 momentum
 Huấn luyện Đánh giá
 Hình 4.6 Tỉ lệ nhận dạng đúng của các thuật toán trên tập huấn luyện và tập đánh giá. 
 Tổng quát ta cũng có thể thấy rằng với thuật toán cho tỉ lệ mất mát cao và các 
thuật toán cho tỉ lệ mất mát thấp sẽ ảnh hưởng đến tỉ lệ nhận dạng đúng của mô hình, 
SGD with momentum và Adam là hai thuật toán có kết quả khá hứa hẹn. Cụ thể tỉ lệ 
 79 
Đánh giá các thuật toán tối ưu đối với mô hình mạng nơ-ron tích chập trong tác vụ nhận diện hình ảnh 
nhận dạng đúng khi sử dụng các thuật toán tối ưu SGD với động lượng, RMSProp, 
Adagrad, Adadelta, Adam lần lượt là 73.9%, 57.3%, 58.9%, 44.5%, 72.9%. 
5. KẾT LUẬN 
 Tổng quát, kết quả từ nghiên cứu trên đã đánh giá được sự tác động của thuật 
toán tối ưu đến việc phân loại đúng kết quả trong bài toán nhận dạng hình ảnh. Nghiên 
cứu cũng cung cấp thêm hiểu biết về thuật toán tối ưu, thông qua các kết quả từ thực 
nghiệm đánh giá, từ đó giúp chúng ta có sự lựa chọn các thuật toán thật hợp lí trong việc 
xây dựng và huấn luyện, đánh giá mô hình mạng. Trong phạm vi bài báo, chúng tôi chỉ 
so sánh các thuật toán phổ biến và trong thực tế còn rất nhiều các thuật toán tối ưu khác. 
Kết quả trên chỉ so sánh và xác định ra thuật toán tối ưu nhất trong phạm vi các thuật 
toán được xét, đối với bộ cơ sở dữ liệu CIFAR-10 và MNIST. Một số thành phần khác 
như kiến trúc, các tham số, siêu tham số và các tập dữ liệu khác chúng tôi sẽ thực hiện 
phân tích và đánh giá ở các nghiên cứu sau. 
 TÀI LIỆU THAM KHẢO 
 [1]. Léon Bottou, Frank E. Curtis, Jorge Nocedal (2016). Optimization Methods for Large-Scale 
 Machine Learning, arXiv:1606.04838 
 [2]. Jonathan T. Barron (2017). A General and Adaptive Robust Loss Function, arXiv:1701.03077, 
 Cornell University 
 [3]. Qian, N. (1999). On the momentum term in gradient descent learning algorithms. Neural 
 Networks: The Official Journal of the International Neural Network Society, 12(1), 145–151. 
 [4]. Sutskever, I., Martens, J., Dahl, G.E. and Hinton, G.E. (2013). On the importance of 
 initialization and momentum in deep learning. ICML (3), Vol 28, pp. 1139—1147 
 [5]. Christian Igel and Michael H usken̈ (2000). Improving the RMSprop Learning Algorithm. 
 [6]. Alexandre Défossez, Léon Bottou, Francis Bach, Nicolas Usunier (2020). On the Convergence 
 of Adam and Adagrad, arXiv:2003.02395 
 [7]. Matthew D. Zeiler (2012), Adadelta: An Adaptive Learning Rate Method, arXiv:1212.5701v1 
 [cs.LG] 22 Dec 2012 
 [8]. Yann LeCun, Courant Institute (1989). The MNIST Database of Handwritten Digits. 
 [9]. Alex Krizhevsky, Vinod Nair and Geoffrey Hinton (2009). The CIFAR-10 dataset 
 80 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 18, Số 1 (2021) 
 EVALUATING OPTIMAL ALGORITHMS FOR CONVOLUTIONAL NEURAL 
 NETWORK IN IMAGE RECOGNITION 
 Vuong Quang Phuoc*, Nguyen Duc Nhat Quang 
 University of Sciences, Hue University 
 *Email: vqphuoc@husc.edu.vn 
 ABSTRACT 
 With an important role in building and training of neural network models, the 
 optimal algorithm is a useful tool in finding the value of the loss function. After that, 
 the network model parameters can be adjusted logically, contributing to an increase 
 of the correct recognition rate in image recognition. The paper gives the closest 
 approach to optimal algorithms as well as commonly used optimal algorithms. To 
 evaluate the optimal algorithms, we selected the Convolutional neural network 
 (CNN) model, the effectiveness of the given algorithms would be identified based 
 on the loss function value and the correct classification rate of network model for 
 two database sets such as MNIST and CIFAR10. In addition, the role of parameters 
 and algorithms that affect the results such as learning rate (LR), number of learning 
 cycles (Epoch), Loss function, Entropy cross function would be clarified in the 
 experimental process. 
 Keywords: Convolutional neural network, optimal algorithms, SGD, RMS, 
 AdaGrad, AdaDelta, Adam. 
 81 
Đánh giá các thuật toán tối ưu đối với mô hình mạng nơ-ron tích chập trong tác vụ nhận diện hình ảnh 
 Vương Quang Phước sinh năm 1990 tại Thừa Thiên Huế. Năm 2013, ông 
 tốt nghiệp kỹ sư chuyên ngành Điện tử viễn thông tại trường Đại học 
 Khoa học, Đại học Huế. Năm 2018, ông nhận bằng thạc sĩ chuyên ngành 
 Kỹ thuật Điện tử tại trường Đại học Bách khoa Đà Nẵng. Hiện nay, ông 
 đang công tác tại Khoa Điện, Điện tử và Công nghệ vật liệu, trường Đại 
 học Khoa học, Đại học Huế. 
 Lĩnh vực nghiên cứu: Hệ thống thông tin quang, mạng Neuron nhân tạo. 
 Nguyễn Đức Nhật Quang sinh năm 1992 tại Thừa Thiên Huế. Năm 2015, 
 ông tốt nghiệp kỹ sư chuyên ngành Điện tử viễn thông tại Trường Đại 
 học Khoa học, Đại học Huế. Năm 2020, ông nhận bằng thạc sĩ chuyên 
 ngành Khoa học máy tính và Kỹ thuật thông tin (CSIE) tại Trường Đại 
 học Quốc gia Thành Công (NCKU), Đài Loan. Hiện nay, ông đang công 
 tác tại Khoa Điện, Điện tử và Công nghệ vật liệu, Trường Đại học Khoa 
 học, Đại học Huế. 
 Lĩnh vực nghiên cứu: Thiết kế vi mạch số, Trí thông minh nhân tạo (AI), 
 Internet vạn vật kết nối (IoT), Hệ thống nhúng. 
 82