Bài giảng Toán rời rạc - Chương: Thuật toán tham lam - Trần Vĩnh Đức
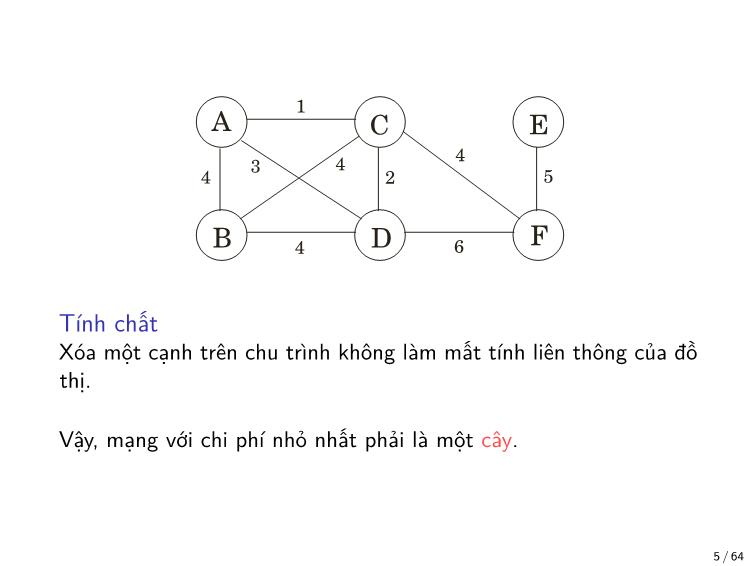
Tính chất
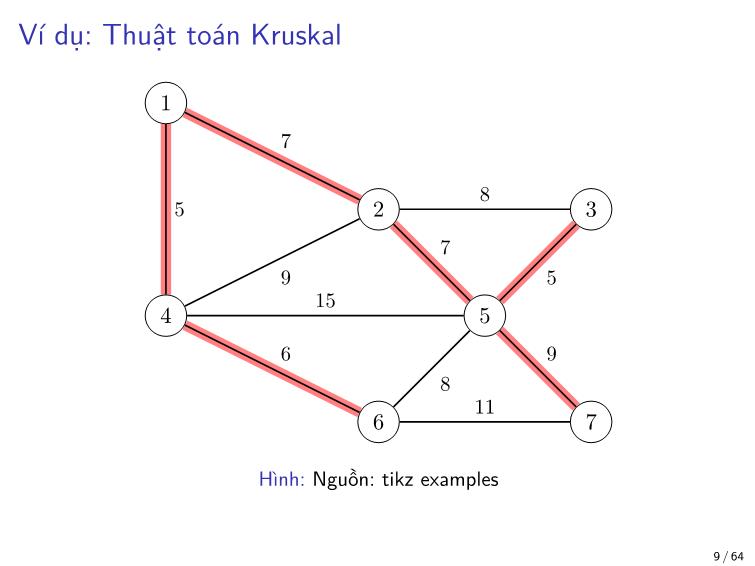
Xóa một cạnh trên chu trình không làm mất tính liên thông của đồ
thị.
Vậy, mạng với chi phí nhỏ nhất phải là một cây.
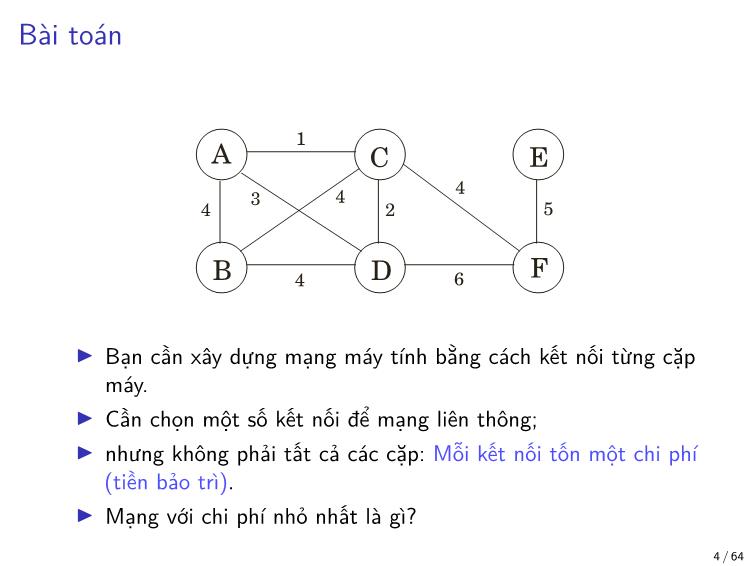
5 / 64Bài toán Cây bao trùm nhỏ nhất (Minimal Spaning Tree)
I Input: Đồ thị vô hướng G = (V, E); mỗi cạnh có trọng số we.
I Output: Một cây T = (V, E′) với E′ ⊆ E, với tổng trọng số
weight(T) = ∑
e∈E′
we
là nhỏ nhất

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương: Thuật toán tham lam - Trần Vĩnh Đức", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương: Thuật toán tham lam - Trần Vĩnh Đức

to n to bring it down to 1 (or below 1). For instance, log 1000 = 4 since log log∗ log log 1000 1.
≤
there will justIn practicebe the first five of the intervals shown; more are needed only if 27 / 64
n 265536, in other words never.
≥
In a sequence of find operations, some may take longer than others. We’ll bound the
overall running time using some creative accounting. Specifically, we will give each node a
certain amount of pocket money, such that the total money doled out is at most n log∗ n dollars.
We will then show that each find takes O(log∗ n) steps, plus some additional amount of time
that can be “paid for” using the pocket money of the nodes involved—one dollar per unit of
time. Thus the overall time for m find’s is O(m log∗ n) plus at most O(n log∗ n).
In more detail, a node receives its allowance as soon as it ceases to be a root, at which point
its rank is fixed. If this rank lies in the interval k + 1, . . . , 2k , the node receives 2k dollars.
{ }
By Property 3, the number of nodes with rank > k is bounded by
n n n
+ + .
2k+1 2k+2 · · · ≤ 2k
Therefore the total money given to nodes in this particular interval is at most n dollars, and
since there are log∗ n intervals, the total money disbursed to all nodes is n log∗ n.
≤
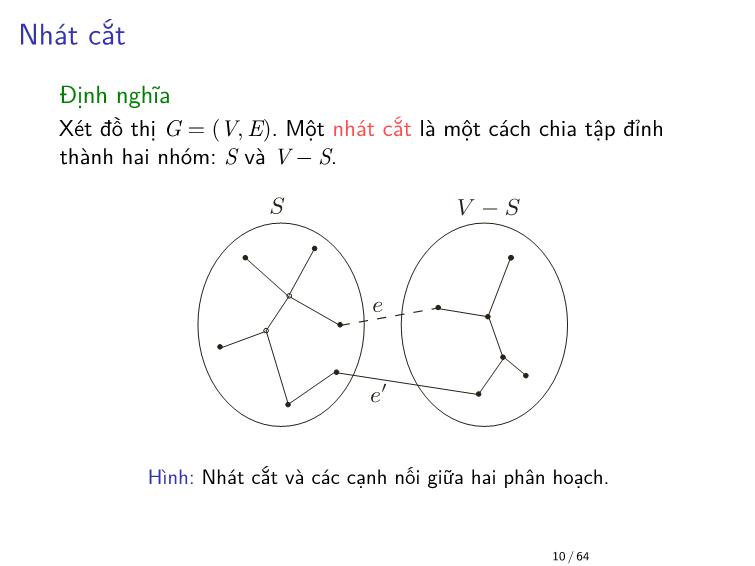
Thuật toán tổng quát dựa trên tính chất cắt
X = {}
Lặp lại các bước sau cho đến khi |X| = |V| − 1:
I Chọn một tập S ⊂ V thỏa mãn: X không chứa cạnh
nối giữa nhát cắt S và V − S.
I Xét e ∈ E là cạnh có trọng số nhỏ nhất nối giữa
nhát cắt S và V − S
I X = X ∪ {e}
28 / 64
Thuật toán Prim
X = {}
Lặp lại các bước sau cho đến khi |X| = |V| − 1:
I Chọn một tập S ⊂ V thỏa mãn: X không chứa cạnh
nối giữa nhát cắt S và V − S.
I Xét e ∈ E là cạnh có trọng số nhỏ nhất nối giữa
nhát cắt S và V − S
I X = X ∪ {e}
Thuật toán Prim
I Tập cạnh X luôn tạo ra một cây con, và
I Tập S được chọn là tập đỉnh của cây con này.
29 / 64
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 151
Figure 5.8 Prim’s algorithm: the edges X form a tree, and S consists of its vertices.
S V − S
X e
Thuật toán Prim
growing to include theI vertexTập cạnhv X luônS of tạosmallest ra một câycost con,: và
̸∈
I Tập S được chọn là tập đỉnh của cây con này.
cost(v) = min w(u, v).
u S
∈
30 / 64
This isreminiscentstrongly s ofalgorithm,Dijkstra’and in fact the pseudocode (F igure 5.9)
is almost identical. The only difference is in the key values by which the priority queue is
ordered. In Prim’s algorithm, the value of a node is the weight of the lightest incoming edge
from set S, whereas in Dijkstra’s it is the length of an entire path to that node from the
starting point. Nonetheless, the two algorithms are similar enough that they have same
the running, whictime h depends on particularthe priority queue implementation.
Figure 5.9 shows Prim’s algorithm at work, on a small six-node graph. Notice how the
final MST is completely specified by the prev array.
Ví dụ: Thuật toán Prim
1
7
8
5 2 3
7
9 5
15
4 5
6 9
8
11
6 7
Hình: Nguồn: tikz examples
31 / 64
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 151
FigureThuật5.8 Prim’ toáns algorithm: Prim vstheDijkstraedges X form a tree, and S consists of its vertices.
S V − S
X e
I Mỗi bước lặp, cây con X sẽ được thêm một cạnh.
growing to include the vertex v S of smallest cost:
I Đây là cạnh có̸∈ trọng số nhỏ nhất nối giữa một đỉnh trong S
và một đỉnh ngoàicostS. (v) = min w(u, v).
u S
∈
I Có nghĩa rằng, thêm vào S đỉnh v ∈/ S có cost nhỏ nhất:
This isreminiscentstrongly s ofalgorithm,Dijkstra’and in fact the pseudocode (F igure 5.9)
is almost identical. The only difference is in the key values by which the priority queue is
cost(v) = min w(u, v)
ordered. In Prim’s algorithm, the value of a nodeu∈isS the weight of the lightest incoming edge
from set S, whereas in Dijkstra’s it is the length of an entire path to that node from the
starting point. Nonetheless, the two algorithms are similar enough that they have same
the running, whictime h depends on particularthe priority32 / 64 queue implementation.
Figure 5.9 shows Prim’s algorithm at work, on a small six-node graph. Notice how the
final MST is completely specified by the prev array.
152 Algorithms
Figure 5.9 Top: Prim’s minimum spanning tree algorithm. Below: An illustration of Prim’s
algorithm, starting at node A. Also shown are a table of cost/prev values, and the final MST.
procedure prim(G, w)
Input: A connected undirected graph G = (V, E) with edge weights we
Output: A minimum spanning tree defined by the array prev
for all u V :
∈
cost(u) =
∞
prev(u) = nil
Pick any initial node u0
cost(u0) = 0
H = makequeue(V ) (priority queue, using cost-values as keys)
while H is not empty:
v = deletemin(H)
for each v, z E:
{ } ∈
if cost(z) > w(v, z):
cost(z) = w(v, z)
prev(z) = v
decreasekey(H, z)
Ví dụ
6 5
A C E A C E
4 1
5 2 3 4
B 2 D 4 F B D F
Tập S A B Set SC AD B E C F D E F
{} ∞ ∞ ∞ ∞ ∞
0/nil /nil /nil 0/nil/nil /nil/nil /nil/nil /nil /nil /nil
{} ∞ ∞ ∞ ∞ ∞
A 5/A A 6/A 4/A 5/∞A/nil 6/∞A /nil4/A /nil /nil
∞ ∞
A, D 2/D A, D2/D 2/D∞/nil 2/D4/D /nil 4/D
∞
A, D, B A, D,1/B B ∞/nil 1/B4/D /nil 4/D
∞
A, D, B, C A, D, B, C 5/C 3/C 5/C 3/C
A, D, B, C, F A, D, B, C, F 4/F 4/F
33 / 64
procedure prim(G, w)
Input: đồ thị vô hướng G = (V, E) với cạnh có trọng số
we.
Output: MST định nghĩa bởi mảng prev.
for all u ∈ V:
cost(u) = ∞
prev(u) = nil (đỉnh trước u khi xây dựng cây)
Chọn tùy ý một đỉnh ban đầu u0
cost(u0) = 0
H = makequeue(V) (dùng các giá trị cost làm khóa)
while H khác rỗng:
v = deletemin(H)
for all edges {v, z} ∈ E:
if cost(z) > w(v, z):
cost(z) = w(v, z)
prev(z) = v (đỉnh trước z là v)
decreasekey(H, z)
34 / 64
Nội dung
Cây bao trùm nhỏ nhất
Mã hóa Huffman
Công thức Horn
Phủ các tập
Sơ đồ nén MP3
1. Số hóa bằng cách lấy mẫu theo khoảng. Tạo ra một dãy
số thực
s1, s2,..., sT
Ví dụ, với tốc độ 44, 100 mẫu trên giây, bản giao hưởng 50
phút có
T = 50×60×44, 100 ≈ 130 triệu.
2. Lượng hóa. Xấp xỉ si bởi giá trị gần nhất thuộc tập hữu hạn
Γ.
3. Mã hóa. Xâu s1s2 ... sT trên bảng chữ Γ được mã hóa ở
dạng nhị phân. (Dùng mã Huffman)
36 / 64
Mã hóa
Ký hiệu Số lần xuất hiện
A 70 triệu
B 3 triệu
C 20 triệu
D 37 triệu
I Bảng chữ Γ = {A, B, C, D} và T = 130 triệu.
I Nếu mã hóa dùng 2 bit cho mỗi ký hiệu, ví dụ
A → 00, B → 01, C → 10, D → 11
ta cần 260 megabits.
I Liệu ta có thể dùng mã độ dài thay đổi để giảm kích thước
bản mã?
37 / 64
Mã độ dài thay đổi
I Dùng các dãy bit độ dài khác nhau để mã hóa các chữ cái.
I Chữ cái xuất hiện thường xuyên hơn sẽ được mã bằng dãy bit
ngắn hơn.
I Vấn đề: Làm thế nào xác định được mỗi chữ bắt đầu và kết
thúc ở đâu trong dãy bit.?
Ví dụ
Cách mã hóa
A → 0, C → 01, D → 11, B → 001
gây ra nhập nhằng khi giải mã
001 → AC
001 → B
38 / 64
Mã tiền tố
Định nghĩa
Mã tiền tố là tập xâu thỏa mãn không có xâu nào là khúc đầu của
xâu khác.
Hãy giải mã dãy bit 10100100?
39 / 64
Kích thước bản mã
Ký hiệu Số lần xuất hiện Từ mã
A 70 triệu 0
B 3 triệu 100
C 20 triệu 101
D 37 triệu 11
I Kích thước bản mã
= (1 × 70 + 3 × 3 + 3 × 20 + 2 × 37) megabits
= 213 megabits
I Cải thiện 17% so với 260 megabits khi dùng mã độ dài cố
định.
40 / 64
Bài toán
I Cho n ký hiệu có tần suất
f1, f2,..., fn.
I Hãy tìm cây ở đó mỗi lá ứng với
một ký hiệu và có chi phí cực tiểu.
∑n
Chi phí của cây = fi · (độ sâu ký hiệu thứ i trong cây)
i=1
41 / 64
Hãy tính chi phí của cây sau.
∑n
Chi phí của cây = fi · (độ sâu ký hiệu thứ i trong cây)
i=1
42 / 64
I
Tần suất nút lá là fi.
I Tần suất nút trong là tổng
tần suất của các lá con cháu của nó.
Mệnh đề
Chi phí của cây là tổng tần suất của mọi nút ngoại trừ nút gốc.
43 / 64
Tối ưu hàm chi phí
∑n
Chi phí của cây = fi · (độ sâu của ký hiệu thứ i trong cây)
i=1
Nhận xét
Hai ký hiệu với tần suất nhỏ nhất sẽ phải ở đáy của cây tối ưu.
44 / 64
Xây dựng cây một cách tham lam
I Tìm hai ký hiệu có tần suất nhỏ nhất, gọi là i và j, và tạo nút
cha của chúng với tần suất fi + fj.
Để đơn giản ký hiệu, ta giả sử chúng là f1 và f2.
I
Mọi cây trong đó f1 và f2 là nút lá anh em có chi phí f1 + f2
cộng với chi phí cho cây gồm n − 1 nút lá của các tần suất:
(f1 + f2), f3, f4,..., fn.
I
Ta đưa về bài toán kích thước nhỏ hơn. Ta loại bỏ f1 và f2
khỏi dãy tần suất và thêm (f1 + f2) vào, và lặp lại.
45 / 64
Xây dựng cây một cách tham lam
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 155
f1 + f2
f5 f4 f3
f1 f2
Hình: Loại f , f và thêm f + f vào dãy tần suất.
The latter problem is just a smaller version1 2 of the1 one2 we started with. So we pull f1 and f2
off the list of frequencies, insert (f1 + f2), and loop. The resulting algorithm can be described
in terms of priority queue operations (as defined on page 120) and takes O(n log n) time if a
46 / 64
binary heap4.5.2)(Sectionis used.
procedure Huffman(f)
Input: An array f[1 n] of frequencies
· · ·
Output: An encoding tree with n leaves
let H be a priority queue of integers, ordered by f
for i = 1 to n: insert(H, i)
for k = n + 1 to 2n 1:
−
i = deletemin(H), j = deletemin(H)
create a node numbered k with children i, j
f[k] = f[i] + f[j]
insert(H, k)
Returning to our toy example: can you tell if the tree of Figure 5.10 is optimal?
procedure Huffman(f)
Input: mảng f[1 ··· n] của các tần suất
Output: Một cây mã hóa với n lá
Xét H là hàng đợi ưu tiên của các số nguyên, thứ tự
bởi f
for i = 1 to n: insert(H, i)
for k = n + 1 to 2n − 1:
i = deletemin(H), j = deletemin(H)
Tạo một nút đánh số k với các con là i, j
f[k] = f[i] + f[j]
insert(H, k)
47 / 64
Nội dung
Cây bao trùm nhỏ nhất
Mã hóa Huffman
Công thức Horn
Phủ các tập
Biến Boolean
I Đối tượng cơ sở trong công thức Horn là biến Boolean, nhận
giá trị true hoặc false.
I Một literal là một biến x hoặc nghịch đảo của nó x (“NOT
x”).
Ví dụ
Biến x, y và z ký hiệu các khả năng sau đây:
x ≡ vụ giết người xảy ra trong bếp
y ≡ người quản gia vô tội
z ≡ ngài đại tá đã ngủ lúc 8 giờ tối
49 / 64
Công thức Horn
Trong công thức Horn, tri thức về các biến được biển diễn bởi hai
loại mệnh đề:
1. Kéo theo, vế trái là một AND của một số các literal dương
và vế phải là một literal dương.
Các khẳng định này có dạng “nếu mệnh đề vế trái mà đúng,
thì vế phải cũng phải đúng”. Ví dụ,
(x ∧ w) ⇒ u
Một trường hợp riêng là dạng đơn ⇒ x với ý nghĩa rằng “x là
true”.
2. Toàn phủ định, bao gồm một OR của một số literal âm.
Ví dụ
(u ∨ v ∨ y)
(“không thể tất cả cùng vô tội”).
50 / 64
Bài toán nhất quán
I Cho một tập các mệnh đề kéo theo hoặc toàn phủ định;
I Hãy xác định liệu chúng có nhất quán. Tức là, có cách gán
true/false cho các biến để thỏa mãn mọi mệnh đề. Đây
cũng gọi là phép gán thỏa được.
Câu hỏi
Hãy xác định liệu các mệnh đề sau có nhất quán:
(w ∧ y ∧ z) ⇒ x, (x ∧ z) ⇒ w, x ⇒ y,
⇒ x, (x ∧ y) ⇒ w, (w ∨ x ∨ y), (z).
51 / 64
Thuật toán tham lam
Input: Một công thức Horn
Output: Một phép gán thỏa được, nếu tồn tại
Đặt mọi biến bằng false
while còn phép kéo theo chưa thỏa mãn:
Đặt biến ở vế phải của phép kéo theo này bằng
true
if mọi mệnh đề toàn phủ định được thỏa mãn:
return phép gán
else:
return ``công thức không thỏa mãn''
52 / 64
Bài tập
Hãy chạy thuật toán với công thức Horn gồm các mệnh đề sau:
(w ∧ y ∧ z) ⇒ x,
(x ∧ z) ⇒ w,
x ⇒ y,
⇒ x,
(x ∧ y) ⇒ w,
(w ∨ x ∨ y),
(z).
53 / 64
Tính đúng đắn của thuật toán
I Nếu return một phép gán, thì phép gán này phải thỏa mãn
cả các mệnh đề kéo theo và các mệnh đề toàn phủ định.
I Ngược lại, ta có bất biến trong vòng lặp while:
Nếu một biến được đặt bằng true, vậy thì nó phải
bằng true trong mọi phép gán thỏa được.
Nếu có một phép gán được tìm thấy sau vòng lặp while mà
không thỏa mãn mệnh đề toàn phủ định, vậy không có phép
gán nào thỏa được.
54 / 64
Nội dung
Cây bao trùm nhỏ nhất
Mã hóa Huffman
Công thức Horn
Phủ các tập
Xây trường học trong các thị trấn
I Mỗi trường phải ở trong một thị trấn và không ai phải đi hơn
30 dặm để tới trường.
I Số trường tối thiểu cần xây là bao nhiêu?
56 / 64
Xây trường học trong các thị trấn
I
Mỗi thị trấn x, đặt Sx là tập thị trấn cách x trong vòng 30
dặm. Một trường tại x sẽ “phủ” các thị trấn này.
I
Cần lấy bao nhiêu tập Sx để phủ mọi thị trấn?
57 / 64
Bài toán phủ tập
I
Input: Một tập B; và các tập S1, S2,..., Sm ⊆ B
I
Output: Một cách chọn các Si sao cho hợp của chúng là B
I Chi phí: Số tập được chọn
58 / 64
Thuật toán tham lam
Lặp lại cho đến khi mọi phần tử của B được phủ:
Chọn tập Si với nhiều phần tử chưa được phủ nhất.
59 / 64
Bài tập
Hãy tìm phủ tối ưu cho tập thị trấn như sau:
60 / 64
Khẳng định
Giả sử B chứa n phần tử và phủ tối ưu gồm k tập. Thuật toán
tham lam sẽ dùng nhiều nhất k ln n tập.
61 / 64
Chứng minh
I
Xét nt là số phần tử vẫn chưa được phủ sau t lần lặp của
thuật toán tham lam. Ta có n0 = n.
I Vì các phần tử này bị phủ bởi k tập tối ưu, nên phải có một
tập với ít nhất nt/k phần tử trong số k tập này.
I Vậy chiến lược tham lam đảm bảo
( ) ( ) ( )
2 t+1
nt 1 1 1
n ≤ n − = n 1 − < n − 1 − < n 1 −
t+1 t k t k t 1 k 0 k
I Do 1 − x ≤ e−x, ta được
( )
1 t
n ≤ n 1 − < n (e−1/k)t = ne−t/k
t 0 k 0
I − ln n
Khi t = k ln n, thì nt < ne = 1, tức là không còn phần tử
nào cần phủ.
62 / 64
160 Algorithms
which is most easily proved by a picture:
x
e−
1 x
− 1
x
0
Thus −x
Hình: Chỉ ra rằng 1 − x ≤ e vớit mọi x, đẳng thức nếu và chỉ nếu x = 0.
1 1/k t t/k
n n 1 < n (e− ) = ne− .
t ≤ 0 − k 0
! " 63 / 64
ln n
At t = k ln n, therefore, nt is strictly less than ne− = 1, which means no elements remain to
be covered.
The ratio between the greedy algorithm’s solution and the optimal solution varies from
input to input but is always less than ln n. And there are certain inputs for which the ratio is
very close to ln n (Exercise 5.33). We call this maximum ratio the approximation factor of the
greedy algorithm. There seems to be a lot of room for improvement, but in fact such hopes are
unjustified: it turns out that under certain widely-held complexity assumptions (which will
be clearer when we reach Chapter 8), there is provably no polynomial-time algorithm with a
smaller approximation factor.
Tỉ suất của thuật toán tham lam
I Tỉ lệ giữa nghiệm của thuật toán tham lam và nghiệm tối ưu
thay đổi theo dữ liệu vào nhưng luôn nhỏ hơn ln n.
I Có một số input tỉ lệ rất gần với ln n.
I Ta gọi tỉ lệ lớn nhất là tỉ suất của thuật toán tham lam.
Nhận xét
Dưới một số giả sử được thừa nhận rộng rãi, ta có thể chứng minh
được rằng: không có thuật toán thời gian đa thức với tỉ suất xấp xỉ
nhỏ hơn.
64 / 64File đính kèm:
 bai_giang_toan_roi_rac_chuong_thuat_toan_tham_lam_tran_vinh.pdf
bai_giang_toan_roi_rac_chuong_thuat_toan_tham_lam_tran_vinh.pdf

