Bài giảng Giải tích II - Chương 3: Tích phân bội hai - Nguyễn Văn Quang
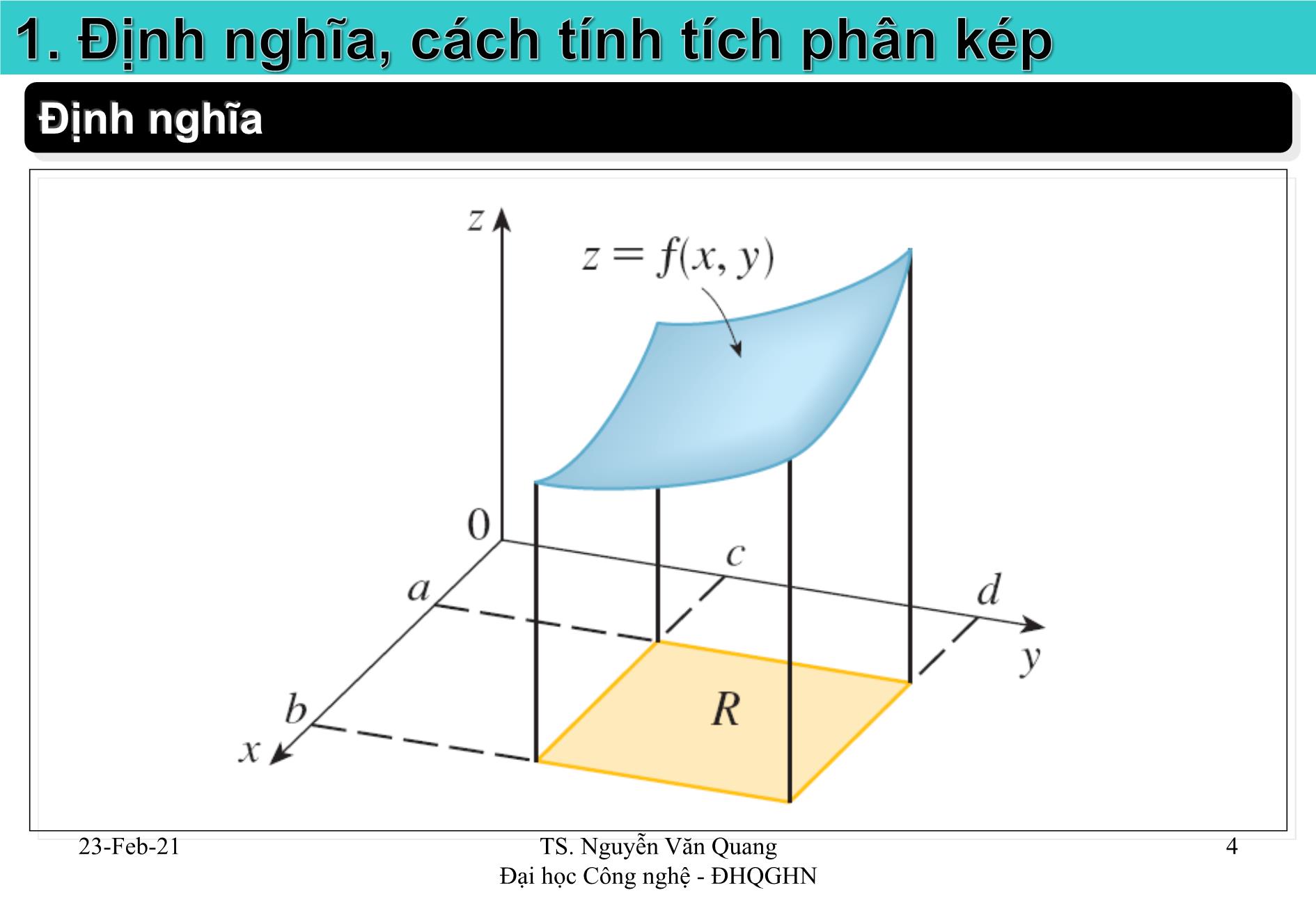
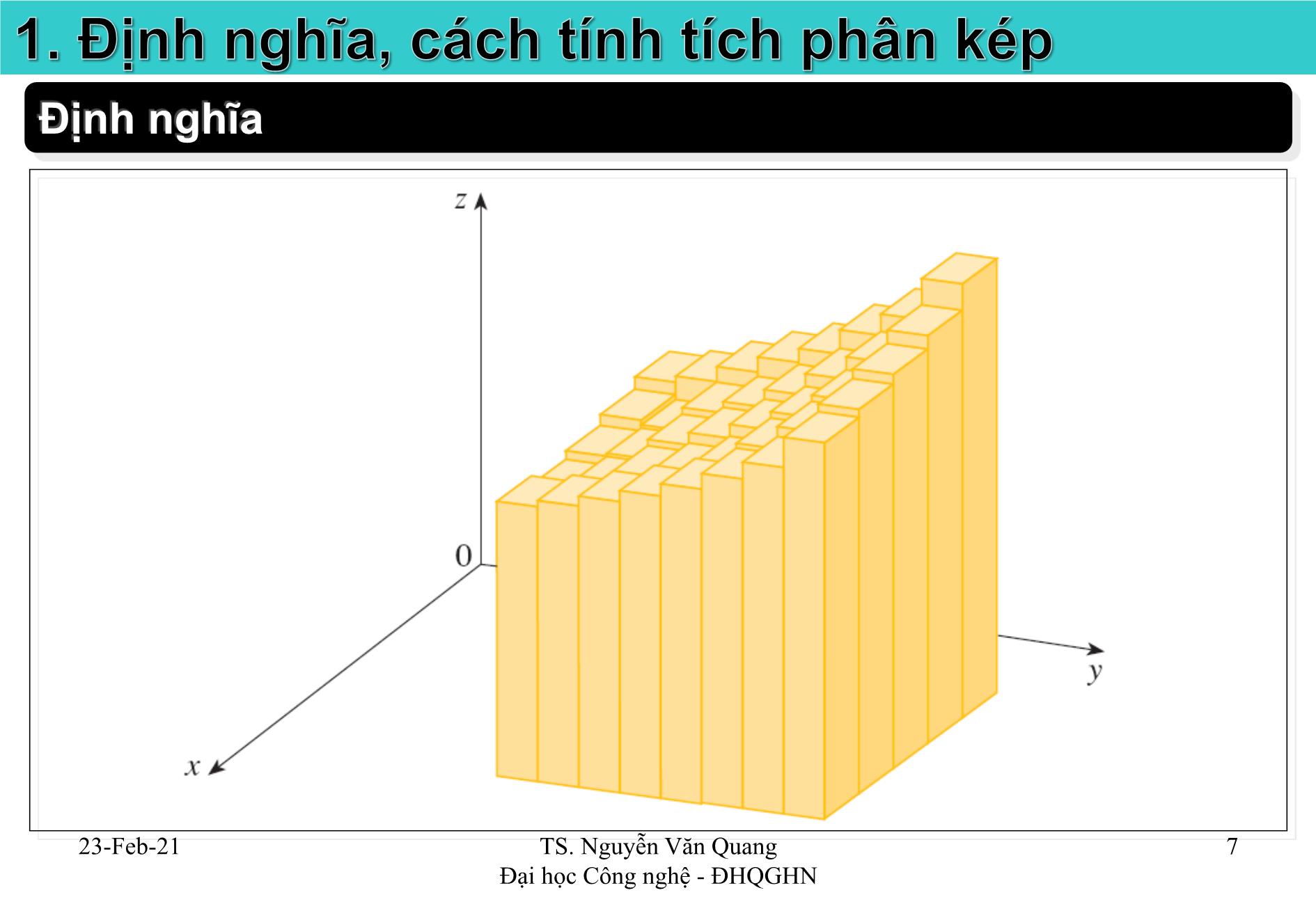
Cho hình trụ được giới hạn trên bởi mặt bậc hai f x y ( , ) 0 ,
giới hạn dưới bởi miền D = [a,b]x[c,d] (đóng, bị chặn).
giới hạn xung quanh bởi những đường thẳng song song Oz, tựa trên biên D.
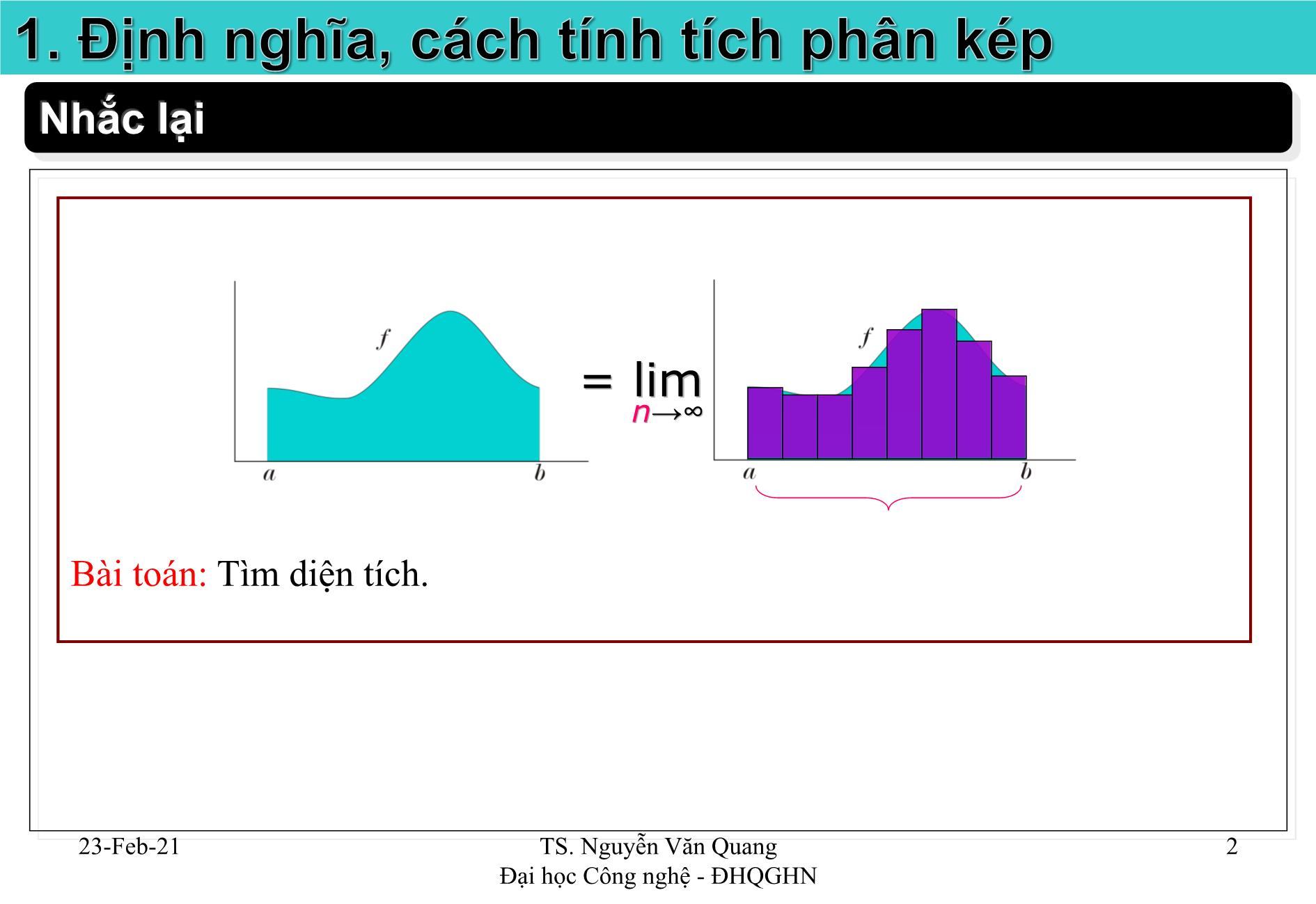
Bài toán: Tìm thể tích hình trụ.
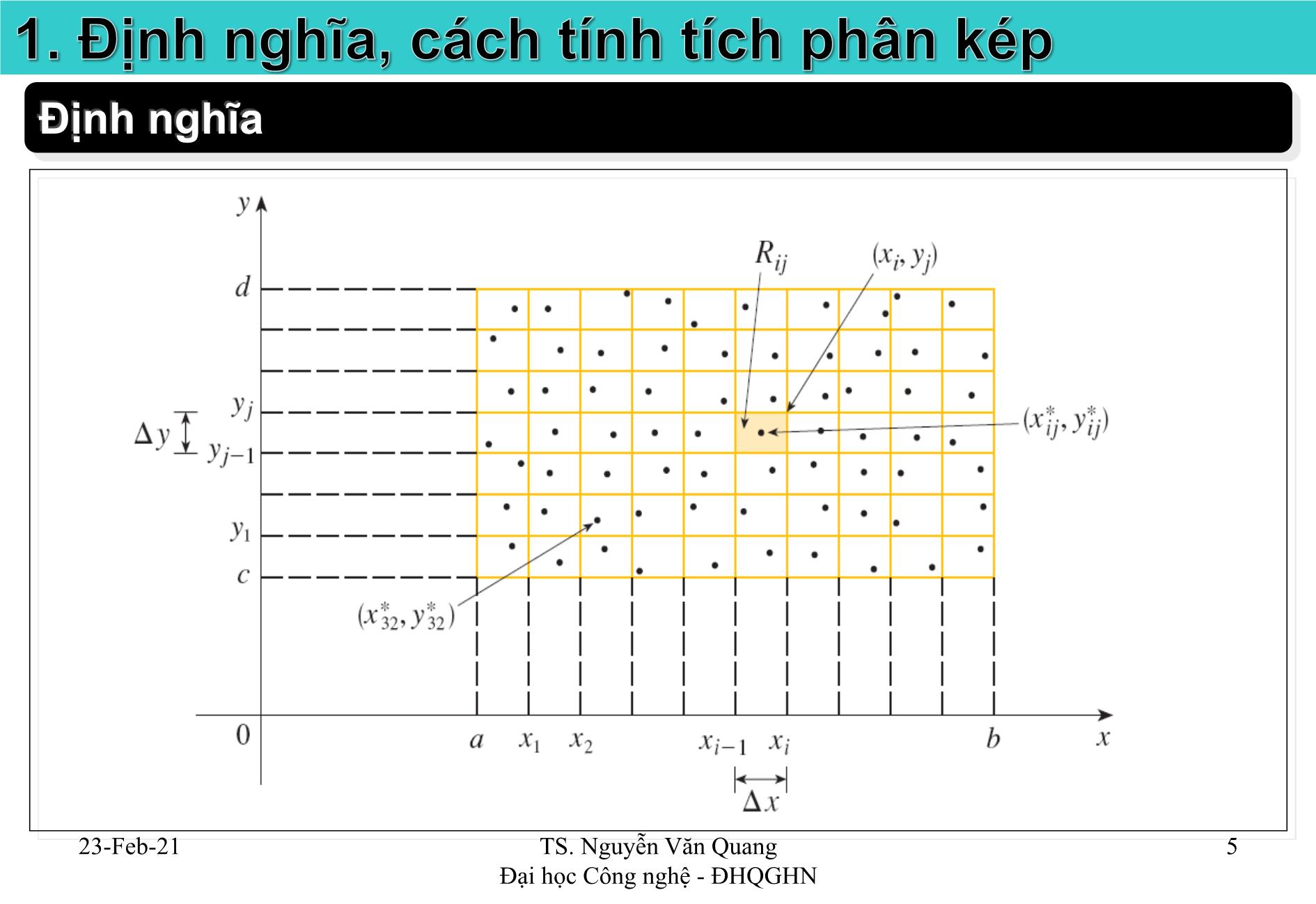
1) Chia D một cách tùy ý ra thành n hình chữ nhật rời nhau: D1, D2, ., Dn.
Có diện tích tương ứng là
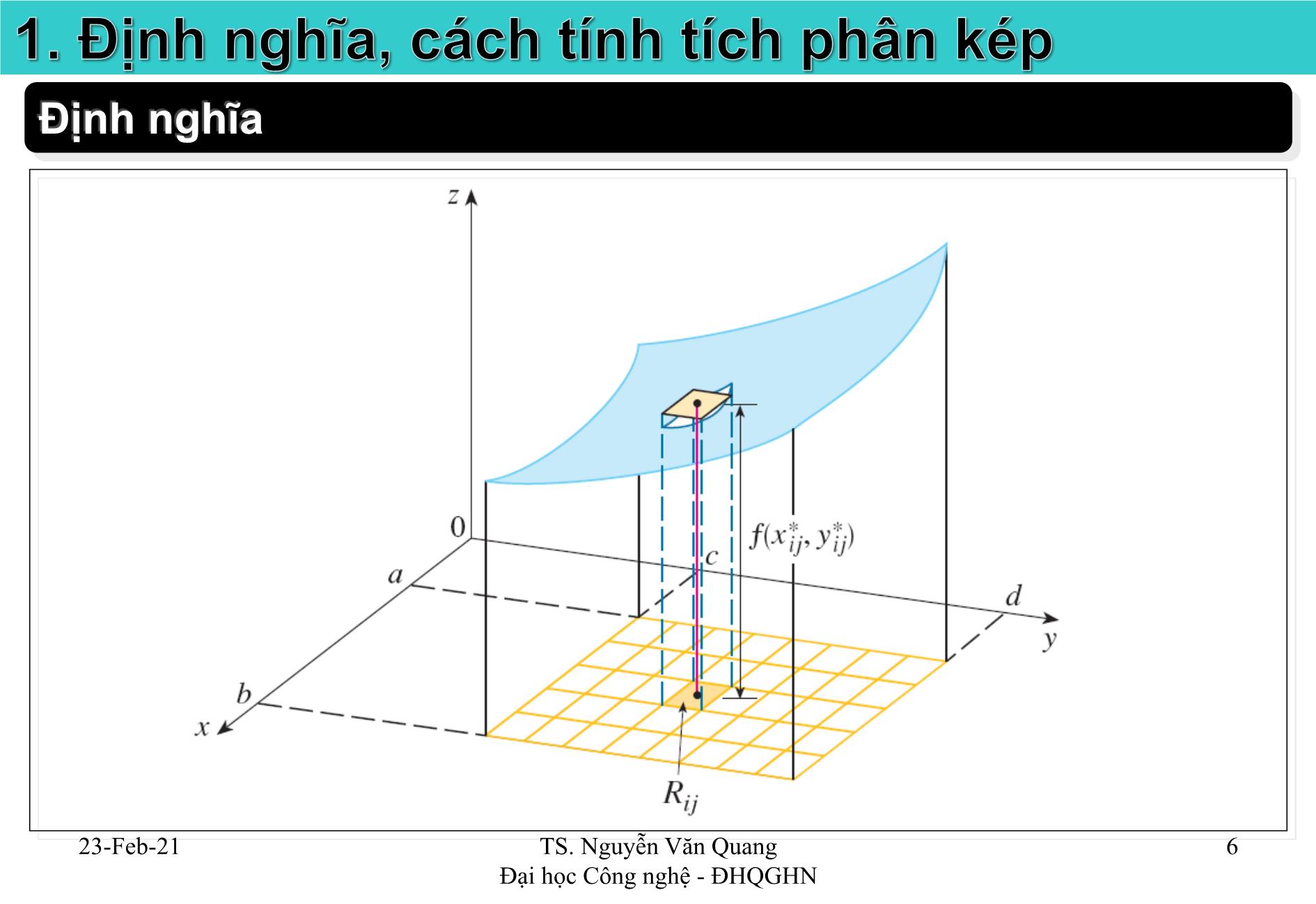
2) Trên mỗi miền lấy tùy ý một điểm M x y D i i i i ( , )
3) Thể tích của vật thể: (tổng Riemann)

Trang 1
Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Giải tích II - Chương 3: Tích phân bội hai - Nguyễn Văn Quang", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Giải tích II - Chương 3: Tích phân bội hai - Nguyễn Văn Quang

QGHN Ví dụ 01 y D : yx 1 01 x Thay đổi cận: D : 0 yx 1 x 1 1 1 2 2 x 2 112 e I dx ex dy ex y dx xex dx x 0 e 00 0 0 220 23-Feb-21 TS. Nguyễn Văn Quang 25 Đại học Công nghệ - ĐHQGHN 11 3 Tính tích phân kép I dysin( x 1) dx 0 y 1 3 Tích phân sin( x 1) dx không tính được (qua các hàm sơ cấp). y 01 y D : yx 1 Thay đổi cận: 01 x D : 2 0 yx 2 1 x 1 2 3 sin(x3 1) yx dx I dxsin( x 1) dy 0 00 0 1 23 cos(1) 1 xsin( x 1) dx 0 3 23-Feb-21 TS. Nguyễn Văn Quang 26 Đại học Công nghệ - ĐHQGHN Ví dụ 1 yy2 Thay đổi thứ tự lấy tích phân I dy f(,) x y dx 00 01 y D : 2 0 x y y Vẽ miền D: Thay đổi cận: 02 x D : 1 1 4x y 1 21 2 I dx f(,) x y dy 0 1 1 4x 2 23-Feb-21 TS. Nguyễn Văn Quang 27 Đại học Công nghệ - ĐHQGHN 2 3 24 y Thay đổi thứ tự lấy tích phân I dy f(,) x y dx 3 12 y2 33 y D : D1 22 12 y x 2 4 y Vẽ miền D: Thay đổi cận: D3 Phải chia D làm 3 miền: 3 x 2 3 D1 : 22 12 x y 4 x x 3 x 2 3 D2 D2 : 4x x22 y 12 x 2 3 x 4 D3 : I fdxdy fdxdy fdxdy 22 44x x y x x DDD1 2 3 23-Feb-21 TS. Nguyễn Văn Quang 28 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Tổng quát, xét phép đổi biến T từ mặt Ouv sang mặt Oxy: ( , 푣) = ( , ) với x và y liên hệ với u và v bởi: = , 푣 ; = ℎ( , 푣) Có thể viết: = ( , 푣), = ( , 푣). Giả sử T là một phép biến thỏa mãn: g và h có đạo hàm riêng bậc nhất liên tục. Nếu ( 1, 푣1) = ( 1, 1), thì ( 1, 1) được gọi là ảnh của điểm ( 1, 푣1). Nếu không có 2 điểm nào có cùng chung 1 ảnh và ngược lại, thì ta gọi T là đổi biến 1-1. 23-Feb-21 TS. Nguyễn Văn Quang 29 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Nếu T là đổi biến 1-1, nó sẽ có một phép biến đổi ngược −1 từ mặt Oxy sang mặt Ouv. Do đó, ta có thể tìm u và v theo x và y : = ( , ), 푣 = ( , ) 23-Feb-21 TS. Nguyễn Văn Quang 30 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Xét một hình chữ nhật nhỏ S trong mặt Ouv: ảnh của S là miền R trong mặt Oxy. Một điểm trên cạnh biên của nó sẽ là: ( 0, 0) = ( 0, 푣0) 23-Feb-21 TS. Nguyễn Văn Quang 31 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Ta có vector vị trí của điểm (u, v): 풓( , 푣) = 풊 + 풋 = ( , 푣) 풊 + ℎ( , 푣) 풋 Phương trình của cạnh dưới của S là: 푣 = 푣0 Ảnh của nó được cho bởi hàm vector 풓( , 푣0). 23-Feb-21 TS. Nguyễn Văn Quang 32 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Nếu một đường cong trong mặt phẳng cho bởi hàm vector: 풓(푡) = (푡) 풊 + (푡) 풋 với 푡 là tham số thì vector tiếp tuyến tại 푡0 đối với đường cong không gian này sẽ là: x y r x i y j i j t t0 t0 t t 23-Feb-21 TS. Nguyễn Văn Quang 33 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Do đó vector tiếp tuyến tại ( 0, 0) đối với đường cong ảnh này sẽ là: xy r g(,)(,) u v i h u v j i j u u0 0 u 0 0 uu 23-Feb-21 TS. Nguyễn Văn Quang 34 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Tương tự, vector tiếp tuyến tại ( 0, 0) đối với đường cong ảnh của cạnh trái của ( = 0) là: xy r g(,)(,) u v i h u v j i j v v0 0 v 0 0 vv 23-Feb-21 TS. Nguyễn Văn Quang 35 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Ta có thể xấp xỉ miền ảnh 푅 = (푆) bởi một hình bình hành xác định bởi các vector cát tuyến: ar (,)u00 u v r(,)uv00 br (,)u00 v v r(uv00 , ) 23-Feb-21 TS. Nguyễn Văn Quang 36 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Tuy nhiên, rr(,)(,)u0 u v 0 u 0 v 0 ru lim u 0 u Nên, r(,)(,).u0 u v 0 r u 0 v 0 u ru Tương tự, r(,)(,).u0 v 0 v r u 0 v 0 v rv 23-Feb-21 TS. Nguyễn Văn Quang 37 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Điều này có nghĩa là ta có thể xấp xỉ R bởi một hình bình hành xác định bởi 2 vector ∆ . 풓 và ∆푣. 풓푣 . 23-Feb-21 TS. Nguyễn Văn Quang 38 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Vậy, có thể xấp xỉ diện tích của R bởi diện tích của hình bình hành này: |(∆ 풓 ) × (∆푣 풓푣)| = |풓 × 풓푣| ∆ ∆푣 Tích có hướng của 2 vector: i j k x y x x xy u u u v r r 0 k k uv uu x y y y xy v v u v 0 vv 23-Feb-21 TS. Nguyễn Văn Quang 39 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Jacobian của biến đổi T cho bởi = ( , 푣) và = ℎ( , 푣) là: xx (,)x yuv x y x y (,)u vyy u v v u uv Với ký hiệu này ta có thể xấp xỉ một diện tích ∆A của R: (,)xy ở đây Jacobian được A u v (,)uv tính tại (u0, v0). 23-Feb-21 TS. Nguyễn Văn Quang 40 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Tiếp theo, ta chia miền S trong mặt Ouv thành các hình chữ nhật nhỏ 푆푖푗 và gọi ảnh của nó trong mặt Oxy là 푅푖푗. 23-Feb-21 TS. Nguyễn Văn Quang 41 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Áp dụng công thức xấp xỉ đối với 푅푖푗 ở trên, ta có xấp xỉ của tích phân 2 lớp của f trên miền R như sau. f(,) x y dxdy R f(,) xij y A (,)xy ở đây Jacobian được f( g ( u , v ), h ( u , v )) u v i j i j tính tại ( , 푣 ). (,)uv 푖 푗 Chú ý đây chính là tổng Riemann của tích phân: (,)xy f( g ( u , v ), h ( u , v )) du dv S (,)uv 23-Feb-21 TS. Nguyễn Văn Quang 42 Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Định lý: Giả sử có phép đổi biến: = , 푣 , = , 푣 ; sao cho phép đổi biến này là 1-1 (có thể trừ trên biên), và 퐽 ≠ 0 (có thể 퐽 = 0 tại một số điểm hữu hạn), khi đó: ( , ) = ( ( , 푣), ( , 푣)). 퐽 . 푣 푣 Trong đó: ′ ′ 휕( , ) 푣 퐽 = = ′ ′ 휕( , 푣) 푣 23-Feb-21 TS. Nguyễn Văn Quang 43 Đại học Công nghệ - ĐHQGHN Định nghĩa Mối liên hệ giữa tọa độ cực và y tọa độ Descartes: xr cos , 0 2 M(,) x y yr sin y r 2 2 2 Chú ý: x y r x x Ví dụ. Phương trình đường tròn tâm 0, bán kính bằng 2: xy22 4 Phương trình đường tròn này trong tọa độ cực là: r 2. 23-Feb-21 TS. Nguyễn Văn Quang 44 Đại học Công nghệ - ĐHQGHN Ví dụ • Phương trình đường tròn tâm (1,0), bán kính bằng 1: x22 y2 x Phương trình đường tròn này trong tọa độ cực là: r2 2 r cos r 2cos • Phương trình đường tròn tâm (0,1), bán kính bằng 1: x22 y2 y Phương trình đường tròn này trong tọa độ cực là: r2 2 r sin r 2sin • Phương trình đường thẳng x = 2 2 Phương trình đường thẳng này trong tọa độ cực là: rrcos 2 cos 23-Feb-21 TS. Nguyễn Văn Quang 45 Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 46 Đại học Công nghệ - ĐHQGHN I f(,) x y dxdy R Qua phép đổi biến: xr cos yr sin Chia [a,b] thành m phần. Chia [,] thành n phần. 23-Feb-21 TS. Nguyễn Văn Quang 47 Đại học Công nghệ - ĐHQGHN rii 1 r r Miền Rij : jj 1 ** Trên Rij lấy một điểm (,)rij 11 r** ( r r ); ( ) i22 i 11 i i i i Diện tích miền Rij là: 11 A r22 r ; ij22 i i 1 () jj 1 1 1 A r22 r r r r r rr* ij2 i i 1 2 i i 11 i i i 23-Feb-21 TS. Nguyễn Văn Quang 48 Đại học Công nghệ - ĐHQGHN **** Tọa độ cực của điểm Rij là: (rri cos j , i sin j ) mn **** Tổng Riemann: Vmn f( r i cos j , r i sin j ) A ij ij 11 mn ***** f( ri cos j , r i sin j ) r i r ij 11 mn ** Đặt g( r , ) r f ( r cos , r sin ) Vmn g(,) r i j r ij 11 mn ***** f( x , y ) dxdy lim f ( ri cos j , r i sin j ) r i A ij R mn, ij 11 mn b ** lim g ( rij , ) r g(,) r drd mn, ij 11 a b f( x , y ) dxdy d f ( r cos , r sin ) r dr Ra 23-Feb-21 TS. Nguyễn Văn Quang 49 Đại học Công nghệ - ĐHQGHN Ví dụ Tính tích phân kép I () x y dxdy , trong đó D là miền phẳng giới hạn bởi: D x2 y 2 1, x 2 y 2 4, y 0, y x xr cos yr sin 0 Dr : 4 12 r 23-Feb-21 TS. Nguyễn Văn Quang 50 Đại học Công nghệ - ĐHQGHN Ví dụ I () x y dxdy D / 4 2 / 4 2 2 I d rcos r sin r dr d cos sin r dr 01 01 2 /4 r3 Id cos sin 3 0 1 /4 81 Id cos sin 0 33 7 I 3 23-Feb-21 TS. Nguyễn Văn Quang 51 Đại học Công nghệ - ĐHQGHN 22 Tính I 4 x y dxdy , trong đó D là miền phẳng giới hạn bởi D x22 y 4, y x , y x 3 (y x) xr cos yr sin Dr : 43 02 r /3 2 2 I d 4 r r dr /4 0 2 I 9 23-Feb-21 TS. Nguyễn Văn Quang 52 Đại học Công nghệ - ĐHQGHN 22 Tính I x y dxdy , trong đó D là miền phẳng giới hạn bởi: D x22 y 2 x , y x . xr cos yr sin Dr : 24 0 r 2cos /4 2cos Id r r dr / 2 0 /4 8 3 16 10 2 Id cos /2 3 9 23-Feb-21 TS. Nguyễn Văn Quang 53 Đại học Công nghệ - ĐHQGHN Tính I ( x 1) dxdy , trong đó D là miền phẳng giới hạn bởi: D x2 y 2 2 x ; x 2 y 2 4 x ; y x ; y x 3 xr cos yr sin Dr : 43 2cos r 4cos /3 4cos I d ( r cos 1) r dr / 4 2cos 37 35 67 3 6 24 23-Feb-21 TS. Nguyễn Văn Quang 54 Đại học Công nghệ - ĐHQGHN Tính I () x y dxdy , trong đó D là miền phẳng giới hạn bởi D x2 y 2 2 x ; x 2 y 2 2 y . xr cos 0 D : 2 yr sin 0 r ? 0 D1 : 4 0 r 2sin D 2 D1 D2 : 42 0 r 2cos 11 I DD12 4 2 4 2 23-Feb-21 TS. Nguyễn Văn Quang 55 Đại học Công nghệ - ĐHQGHN Tọa độ cực suy rộng 2 2 2 Trường hợp 1. Miền phẳng D là hình tròn: ()()x x00 y y a Dùng phép đổi biến: x x0 r cos y y0 r sin Khi đó định thức Jacobi: xxr cos r .sin J r yyr sin r .cos Khi lấy cận của r , ta coi như gốc tọa độ dời về tâm hình tròn. 23-Feb-21 TS. Nguyễn Văn Quang 56 Đại học Công nghệ - ĐHQGHN Tọa độ cực suy rộng xy22 Trường hợp 2. Miền phẳng D là Ellipse: 1;ab 0, 0 ab22 x Dùng phép đổi biến: r cos a y r sin b Khi đó định thức Jacobi: xxr a.cos ar .sin J a.. b r yyr b.sin br .cos 02 Khi đó cận của r,: 01 r 23-Feb-21 TS. Nguyễn Văn Quang 57 Đại học Công nghệ - ĐHQGHN Tính I (2 x y ) dxdy, trong đó D là miền phẳng giới hạn bởi D (x 1)22 ( y 2) 4; x 1. Gốc tọa độ dời về đây xr 1 cos yr 2 sin Dr : 22 0 r 2 / 2 2 I d 2(1 r cos ) (2 r sin ) r dr / 2 0 32 8 3 23-Feb-21 TS. Nguyễn Văn Quang 58 Đại học Công nghệ - ĐHQGHN Tính I ( x 1) dxdy , trong đó D là miền phẳng giới hạn bởi D xy22 1;yx 0; 0 94 x r cos 3 y r sin 2 0 Dr : 2 01 r /2 1 3 I d 3 rcos 1 3 2 r dr 6 00 2 23-Feb-21 TS. Nguyễn Văn Quang 59 Đại học Công nghệ - ĐHQGHN Tính I xdxdy , trong đó D là miền phẳng giới hạn bởi D x2 y2 1; y 0; y x 3 x 0 r cos 3 Dr : 3 01 r yr sin sin yr/ tg cos xr/( 3) Vì đường y = x nên tg 3 3 /3 1 3 I d 3 rcos 31 r dr 00 2 23-Feb-21 TS. Nguyễn Văn Quang 60 Đại học Công nghệ - ĐHQGHN Diện tích miền D: SD dxdy Dxy Tính diện tích miền D giới hạn bởi: x2 y 2 2 y ; x 2 y 2 6 y ; y x 3; x 0 Diện tích miền D là: /2 6sin SD dxdy d rdr D /3 2sin 6sin /2 2 /2 r 2 SdD 16sin d 2 /3 2sin /3 4 S 23 D 3 23-Feb-21 TS. Nguyễn Văn Quang 61 Đại học Công nghệ - ĐHQGHN Tính thể tích Để tính thể tích khối : 1) Xác định mặt giới hạn bên trên: z z2 (,) x y 2) Xác định mặt giới hạn bên dưới: z z1(,) x y 3) Xác định hình chiếu của xuống Oxy: D xy Pr Oxy V z x,, y z x y dxdy 21 Dxy Chú ý: 1) Có thể chiếu Ω xuống Oxz, hoặc Oyz. Khi đó mặt phía trên, mặt phía dưới phải theo hướng chiếu xuống. 2) Để tìm hình chiếu của Ω xuống Oxy, ta khử z trong các phương trình của Ω. 23-Feb-21 TS. Nguyễn Văn Quang 62 Đại học Công nghệ - ĐHQGHN Tính thể tích vật thể giới hạn bởi: z ( x 1)22 y ; 2 x z 2 Mặt phía trên: z z2 ( x , y ) 2 2 x 22 Mặt phía dưới: z z1( x , y ) ( x 1) y Hình chiếu: khử z trong 2 phương trình: (x 1)22 y 2 2 x xy22 1 Hình chiếu D:1 x22 y V z21 z dxdy xy22 1 23-Feb-21 TS. Nguyễn Văn Quang 63 Đại học Công nghệ - ĐHQGHN Ví dụ 22 V ()(22 x xx 21 y ) dxdy xy22 1 22 V 1 x y dxdy xy22 1 xr cos Đổi sang tọa độ cực: yr sin 1 21 2 24 2 rr V d 1 r r dr d 00 0 24 0 V 2 23-Feb-21 TS. Nguyễn Văn Quang 64 Đại học Công nghệ - ĐHQGHN Tính thể tích vật thể giới hạn bởi: z x2 y 2; y x 2 ; y 1; z 0 Mặt trên: z x22 y Mặt phía dưới: z 0 Hình chiếu: D D 23-Feb-21 TS. Nguyễn Văn Quang 65 Đại học Công nghệ - ĐHQGHN 22 V x y 0 dxdy D 11 x D : 2 xy 1 11 22 V dx x y dy 1 x2 1 1 3 2 y V xy dx 1 3 x2 1 6 241 x 88 V x x dx 1 33 105 23-Feb-21 TS. Nguyễn Văn Quang 66 Đại học Công nghệ - ĐHQGHN Tính thể tích vật thể giới hạn bởi: z 2 x 22 y 1, x y 1 và các mặt tọa độ. Mặt phía trên: z 21 x22 y Mặt phía dưới: z 0 Hình chiếu: là tam giác màu đỏ. A 0 B 22 3 Mặt dưới V 2 x y 1 0 dxdy OAB 4 23-Feb-21 TS. Nguyễn Văn Quang 67 Đại học Công nghệ - ĐHQGHN Tính thể tích vật thể giới hạn bởi: z 4 y22 ; z y 2; x 1; x 2. z Có thể chiếu xuống Oxy tương tự các ví dụ trước. Chiếu vật thể xuống Oyz: Mặt phía trên: x 2 Mặt phía dưới: x 1 y x 23-Feb-21 TS. Nguyễn Văn Quang 68 Đại học Công nghệ - ĐHQGHN Thể tích vật thể cần tính: z V x21(,)(,) y z x y z dydz Dyz D 1 4 y2 V dy2 ( 1) dz 1 2 y2 1 2 V 3 z4 y dy 2 y2 1 y 1 22 V 3 4 y 2 y dy 1 V 8. 23-Feb-21 TS. Nguyễn Văn Quang 69 Đại học Công nghệ - ĐHQGHN Diện tích mặt cong Mặt S cho bởi phương trình = ( , ), D là hình chiếu của S xuống Oxy. Chia miền D thành n miền con D1, D2, ..., Dn. Khi đó tương ứng, S được chia thành các mặt con S1, S2, ..., Sn . Diện tích tương ứng: ∆푆1, ∆푆2, ⋯ , ∆푆푛 . Lấy điểm tùy ỳ Pi( x i , y i ,0) D i . Tương ứng với điểm M i(,,). x i y i z i S i Gọi Ti là mặt tiếp diện với Si tại Mi . Và Ti là mảnh có hình chiếu xuống Oxy là Di 23-Feb-21 TS. Nguyễn Văn Quang 70 Đại học Công nghệ - ĐHQGHN Diện tích mặt cong Với Di nhỏ, ta coi diện tích của Ti là diện tích gần đúng của mảnh Si : nn SSST ii () ii 11 Gọi i là góc giữa hai mảnh Di và Ti : SDST(i ) ( i ) cos i Ta có i là góc giữa pháp tuyến tại Mi với mặt S và trục Oz. Véctơ pháp của S tại Mi : n Mi z x( x i , y i ), z y ( x i , y i ),1 1 cos i 2 2 zx( x i , y i ) z y ( x i , y i ) 1 23-Feb-21 TS. Nguyễn Văn Quang 71 Đại học Công nghệ - ĐHQGHN nn 2 2 S ST()i zxy x (,) i i zxy y (,)1() i i SD i ii 11 n 2 2 S lim z x z y 1 S ( D i ) n i 1 Diện tích mặt cong có phương trình = ( , ), có hình chiếu xuống mặt phẳng Oxy là Dxy được tính bởi công thức: 2 S 1 z 2 z dxdy xy Dxy 23-Feb-21 TS. Nguyễn Văn Quang 72 Đại học Công nghệ - ĐHQGHN Tính diện tích phần mặt paraboloid z 1 x 22 y nằm trong hình trụ: xy22 1 Hình chiếu của S xuống Oxy: D:1 x22 y Phương trình mặt S: z 1 x22 y z xy 2 x ; z 2 y Diện tích phần mặt paraboloid: 2 2 S 1 z xy z dxdy D 21 22 2 (5 5 1) S 1 4 x 4 y dxdy d 14 r r dr xy22 1 00 6 23-Feb-21 TS. Nguyễn Văn Quang 73 Đại học Công nghệ - ĐHQGHN 23-Feb-21 74 23-Feb-21 75 23-Feb-21 76
File đính kèm:
 bai_giang_giai_tich_ii_chuong_3_tich_phan_boi_hai_nguyen_van.pdf
bai_giang_giai_tich_ii_chuong_3_tich_phan_boi_hai_nguyen_van.pdf

