Bài giảng Toán rời rạc - Chương: Đếm - Trần Vĩnh Đức

 Đếm
Trần Vĩnh Đức
 HUST
 1 / 48
Tài liệu tham khảo
 ▶ E.Lehman, T. Leighton, A. Meyer, Mathematics for Computer
 Science, 2015.
 2 / 48
Nội dung
 Tập, dãy, và ánh xạ
 Luật ánh xạ
 Luật tích và luật tổng
 Nguyên lý bù trừ
 Luật BOOKEEPER
 Chứng minh tổ hợp
Dãy và tập
 ▶ Dãy: có thứ tự, các phần tử có thể trùng nhau
 (a, b, a) ≠ (b, a, a)
 ▶ Tập: không thứ tự, các phần tử không trùng nhau
 {a, b, c} = {b, a, c}
 4 / 48
Định nghĩa
Một hoán vị của một tập S là một dãy chứa mỗi phần tử của S
đúng một lần.
 5 / 48
Số hoán vị của một tập
 ▶ Tập {a, b, c} có 6 hoán vị:
 { (a, b, c), (b, c, a), (c, a, b),
 (c, b, a), (b, a, c), (a, c, b) }
 ▶ Số hoán vị của tập n phần tử là
 n! = n(n − 1) ··· 1
 6 / 48
Định nghĩa
Một ánh xạ
 f : X → Y
là một quy tắc cho tương ứng mỗi phần tử của X với đúng một
phần tử của Y.
 7 / 48
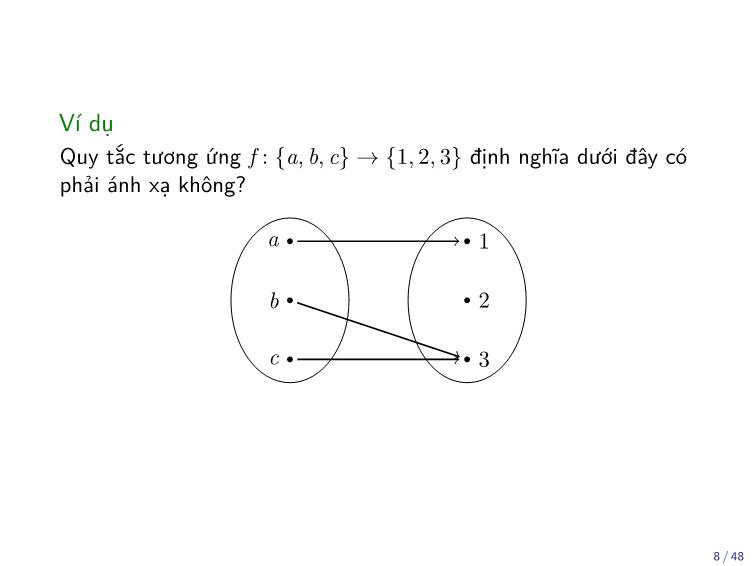
Ví dụ
Quy tắc tương ứng f : {a, b, c} → {1, 2, 3} định nghĩa dưới đây có
phải ánh xạ không?
 a 1
 b 2
 c 3
 8 / 48
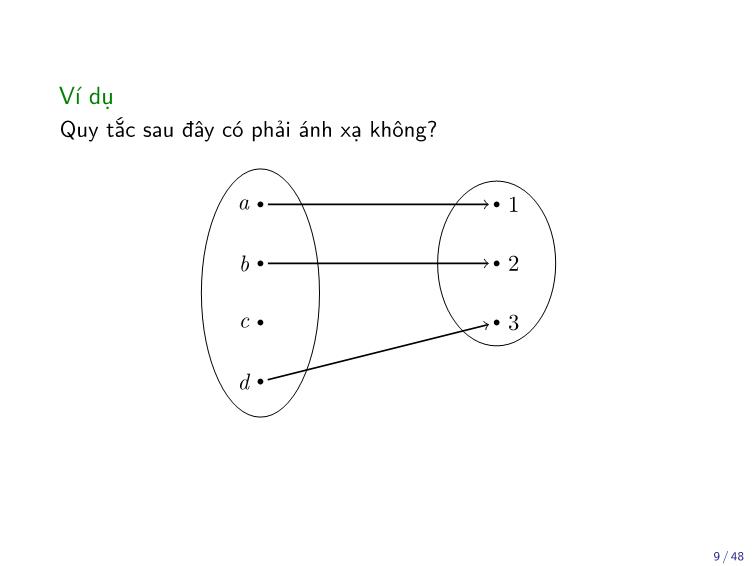
Ví dụ
Quy tắc sau đây có phải ánh xạ không?
 a 1
 b 2
 c 3
 d
 9 / 48
Định nghĩa
Ánh xạ f : X → Y là
 ▶ toàn ánh nếu mỗi phần tử của Y đều có ít nhất một phần tử
 tương ứng từ X.
 ▶ đơn ánh nếu mỗi phần tử của Y đều có nhiều nhất một phần
 tử tương ứng từ X.
 ▶ song ánh nếu mỗi phần tử của Y đều có chính xác một phần
 tử tương ứng từ X.
 10 / 48
Ví dụ
 Ánh xạ dưới đây là đơn ánh hay toàn ánh hay song ánh?
 a 1
 b 2
 c 3
 d
 11 / 48
Ví dụ
Xét hoán vị (a1, a2, ··· , an) của tập S = {a1, a2, ··· , an}. Ánh xạ
 π : {a1, a2,..., an} → {1, 2,..., n}
định nghĩa bởi
 π(ai) = i
là song ánh. Tại sao?
 12 / 48
Nội dung
 Tập, dãy, và ánh xạ
 Luật ánh xạ
 Luật tích và luật tổng
 Nguyên lý bù trừ
 Luật BOOKEEPER
 Chứng minh tổ hợp
Định lý
Nếu ánh xạ f : X → Y là
 ▶ toàn ánh thì |X| ≥ |Y|.
 ▶ đơn ánh thì |X| ≤ |Y|.
 ▶ song ánh thì |X| = |Y|.
 14 / 48
Định lý
Số cây gán nhãn với n đỉnh là nn−2.
 0
 5 3
 2 4 12
 1
Prüfer(T) ←→ 8 9 7
 10 6 16
 15 13
 11
 14
 15 / 48
Ví dụ
Có bao nhiêu cách chọn 12 chiếc bánh từ 5 loại bánh sô cô la,
chanh, có đường, kem, nguyên chất?
 ▶ X = tập mọi cách chọn 12 chiếc bánh từ 5 loại bánh.
 ▶ Y = tập mọi xâu 16 bit có đúng 4 số 1.
 ▶ Song ánh từ X đến Y
 |{z}0 0 1 |{z} 1 0| 0 0{z 0 0 0} 1|{z} 0 0 1|{z} 0 0
 sô cô la chanh có đường kem nguyên chất
 ▶ |X| = |Y|
 16 / 48
Ví dụ
 ▶ Xét song ánh từ các tập con của X = {1, 2,..., n} tới dãy
 n-bit
 S → (b1,..., bn)
 với {
 1 nếu i ∈ S
 bi =
 0 nếu i ∈/ S
 ▶ Số dãy n-bit là 2n.
 ▶ Vậy X có 2n tập con.
 17 / 48
Ánh Xạ “k đến 1”
 Định nghĩa
 Ánh xạ f : X → Y gọi là ánh xạ “k đến 1” nếu nó ánh xạ đúng k
 phần tử của X tới mỗi phần tử của Y.
 Song ánh là ánh xạ “1 đến 1”
 18 / 48
Luật chia (tổng quát hóa của luật song ánh)
 ▶ Nếu f : X → Y là ánh xạ “k đến 1”, thì
 |X| = k · |Y|.
 ▶ Nếu f là song ánh vậy |X| = |Y|.
 19 / 48
Ví dụ
Có bao nhiêu cách đặt hai quân cờ giống nhau lên bàn cờ 8 × 8
sao cho chúng không chung hàng và không chung cột ?
 ▶ Y = tập mọi cấu hình hợp lệ cho hai quân cờ.
 ▶ X = mọi dãy
 (|h1{z, c}1, h|2{z, c}2)
 quân1 quân2
 thỏa mãn h1 ≠ h2 và c1 ≠ c2.
 ▶ Có một ánh xạ “2 đến 1” từ X lên Y. Tại sao?
 ▶ Vậy
 |X| 8 × 8 × 7 × 7
 |Y| = = .
 2 2
 20 / 48
Nội dung
 Tập, dãy, và ánh xạ
 Luật ánh xạ
 Luật tích và luật tổng
 Nguyên lý bù trừ
 Luật BOOKEEPER
 Chứng minh tổ hợp
Luật tích
 Định nghĩa
 A1 × A2 × · · · × An = {(a1, ··· , an) | ai ∈ Ai}
 Định lý
 Nếu A1,..., An là các tập hữu hạn, vậy thì
 |A1 × A2 × · · · × An| = |A1| × |A2| × · · · × |An|.
 22 / 48
Luật tổng
 Định lý
 Nếu A1, A2,..., An là các tập rời nhau, vậy
 |A1 ∪ A2 ∪ · · · ∪ An| = |A1| + |A2| + ··· + |An|.
 23 / 48
Bài toán
Có bao nhiêu cách chọn trong nhóm n người một ủy ban ba người
trong đó một người làm chủ tịch, một người làm thư ký, và một
người làm tư vấn?
 24 / 48
Lời giải
 ▶ Mỗi cách chọn một ủy ban
 ( |{z}x , |{z}y , |{z}x )
 chủ tịch thư ký tư vấn
 ▶ với n người có thể làm chủ tịch,
 ▶ còn lại n − 1 người có thể làm thư ký (trừ x),
 ▶ còn lại n − 2 người có thể làm tư vấn (trừ x và y).
 ▶ Vậy có n(n − 1)(n − 2) cách chọn.
 25 / 48
Bài toán
 ▶ Số seri của các tờ tiền có dạng
 MQ 09 19 99 99
 ▶ Tờ tiền khuyết số nếu có một chữ số xuất hiện hơn một lần
 trong số seri gồm 8 chữ số.
 ▶ Tờ tiền khuyết số có phổ biến không?
 26 / 48
Bài toán
Đếm xem có bao nhiêu mật khẩu thỏa mãn 4 yêu cầu sau đây:
 1. Dài từ 6 đến 8 ký hiệu;
 2. Phải bắt đầu bằng một chữ cái;
 3. Chỉ gồm 26 chữ cái thường hoặc 26 chữ cái hoa hoặc các số 0
 đến 9;
 4. Có phân biệt chữ hoa chữ thường.
 27 / 48
Nội dung
 Tập, dãy, và ánh xạ
 Luật ánh xạ
 Luật tích và luật tổng
 Nguyên lý bù trừ
 Luật BOOKEEPER
 Chứng minh tổ hợp
 A ∩ B
 A B
Theo luật tổng ta có:
 |A| = |A \ B| + |A ∩ B|
 |B| = |B \ A| + |A ∩ B|
 |A ∪ B| = |A \ B| + |A ∩ B| + |B \ A|
 29 / 48
Nguyên lý bù trừ cho hai tập
 |A ∪ B| = |A| + |B| − |A ∩ B|.
 30 / 48
Nguyên lý bù trừ cho ba tập
 |A ∪ B ∪ C| = |A| + |B| + |C|
 − |A ∩ B| − |B ∩ C| − |A ∩ C|
 + |A ∩ B ∩ C|.
 B
 A C
 31 / 48
Nguyên lý bù trừ
 ∑n
 |S1 ∪ S2 ∪ · · · ∪ Sn| = |Si|
 i=1 ∑
 − |Si ∩ Sj|
 ≤ ≤
 1 i<∑j n
 + |Si ∩ Sj ∩ Sk| + ···
 1≤i<j<k≤n
 − n−1| ∩n |
 ( 1) i=1 Si .
 32 / 48
Nguyên lý bù trừ (cách viết khác)
 ∑ ∩ 
 | ∪ ∪ · · · ∪ | − |I|−1  
 S1 S2 Sn = ( 1)  Si
 ∅̸=I⊆{1,2,...,n} i∈I
 33 / 48
Bài toán
 ▶ Có bao nhiêu hoán vị của tập {0, 1,..., 9} có chứa (liền
 nhau) 42, 04 hoặc 60?
 ▶ Ví dụ, hoán vị sau đây chứa 60 và 04.
 (7, 2, 5, 6, 0, 4, 3, 5, 1, 9)
 34 / 48
Bài toán (François Édouard Anatole Lucas, 1894)
Cho một cái bàn tròn và m cặp vợ chồng, có bao nhiêu cách để
xếp họ ngồi nam nữ xem kẽ sao cho không cặp vợ chồng nào ngồi
kề nhau?
 35 / 48
Nội dung
 Tập, dãy, và ánh xạ
 Luật ánh xạ
 Luật tích và luật tổng
 Nguyên lý bù trừ
 Luật BOOKEEPER
 Chứng minh tổ hợp
Định lý (Luật BOOKEEPER)
 ▶
 Xét k chữ phân biệt c1, c2,..., ck.
 ▶
 Số dãy gồm n1 chữ c1, n2 chữ c2, ... , và nk chữ ck là
 ( )
 n + n + ··· + n (n + n + ··· + n )!
 1 2 k = 1 2 k
 n1, n2, ··· , nk n1!n2! ··· nk!
 37 / 48
Định lý (Công thức nhị thức)
 ( ) ( )
 n n n!
 = =
 k, n − k k k!(n − k)!
 38 / 48
Ví dụ
Số dãy 16-bit chứa đúng 4 bit 1 là
 ( )
 16 16!
 = .
 4 4!12!
Đây chính là số cách chọn tập con 4 phần tử từ tập 16 phần tử.
 39 / 48
Ví dụ (Luật tập con)
Số tập con k phần tử của tập n phần tử là
 ( )
 n
 .
 k
 40 / 48
Định lý (Hệ số nhị thức)
Với mọi n ≥ 0 ta có
 ( )
 ∑n n
 (a + b)n = an−kbk.
 k
 k=0
 ▶ (a + b)2 = aa + ab + ba + bb = a2 + 2ab + b2
 ▶ (a + b)3 =
 aaa + aab + aba + baa + abb + bab + bba + bbb
 = a3 + 3a2b + 3b2a + b3
 ( )
 ▶ − n
 Số dãy độ dài n chứa k chữ a và (n k) chữ b là k .
 41 / 48
Nội dung
 Tập, dãy, và ánh xạ
 Luật ánh xạ
 Luật tích và luật tổng
 Nguyên lý bù trừ
 Luật BOOKEEPER
 Chứng minh tổ hợp
Ví dụ
 ▶ Có n chiếc áo phân biệt,
 ( )
 ▶ Số cách giữ lại k chiếc áo là n .
 k ( )
 ▶ − n
 Số cách bỏ đi n k chiếc áo là n−k .
 ▶ Vậy ta có ( ) ( )
 n n n!
 = =
 k n − k k!(n − k)!
 43 / 48
Ví dụ
 ▶ Chọn một đội gồm k sinh viên trong số n sinh viên.
 ( )
 −
 ▶ Số đội có Bob là n 1 .
 k−1 ( )
 ▶ n−1
 Số đội không có Bob là k .
 ▶ Vậy ta có (đẳng thức Pascal)
 ( ) ( ) ( )
 n − 1 n − 1 n
 + = .
 k − 1 k k
 44 / 48
Đếm bằng hai cách
 1. Định nghĩa S.
 2. Chứng minh |S| = n (một cách đếm).
 3. Chứng minh |S| = m (một cách đếm khác).
 4. Kết luận m = n.
 45 / 48
Định lý
 ( ) ( ) ( )
 ∑n n 2n 3n
 · = .
 r n − r n
 r=0
 46 / 48
Chứng minh
 ▶ S = các bộ bài gồm n quân chọn từ n quân đỏ và 2n quân
 đen trên bàn.
 ▶ Vậy ( )
 3n
 |S| = .
 n
 47 / 48
Chứng minh 2
 ▶ Số bộ bài với đúng r quân đỏ là
 ( )( )
 n 2n
 r n − r
 ▶ Số quân đỏ có thể từ 0 đến n nên ta có
 ( )( )
 ∑n n 2n
 |S| = .
 r n − r
 r=0
 48 / 48