A study of fixed points and hopf bifurcation of hindmarshrose model
In this article, a class of Hindmarsh-Rose model is studied. First, all necessary
conditions for the parameters of system are found in order to have one stable
fixed point which presents the resting state for this famous model. After that, using
the Hopf’s theorem proofs analytically the existence of a Hopf bifurcation, which
is a critical point where a system’s stability switches and a periodic solution
arises. More precisely, it is a local bifurcation in which a fixed point of a
dynamical system loses stability, as a pair of complex conjugate eigenvalues cross
the complex plane imaginary axis. Moreover, with the suitable assumptions for
the dynamical system, a small-amplitude limit cycle branches from the fixed point.

Trang 1

Trang 2

Trang 3
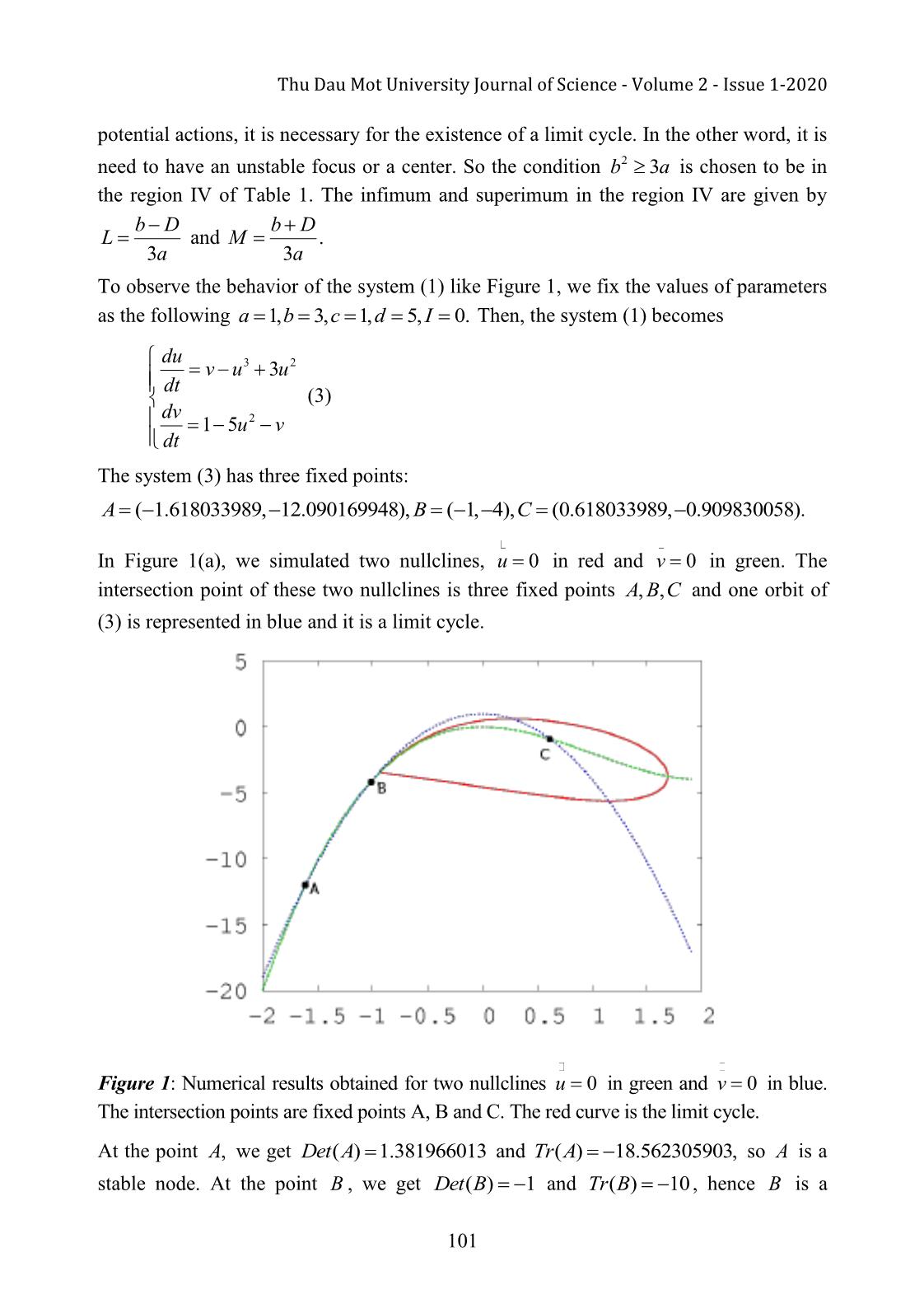
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
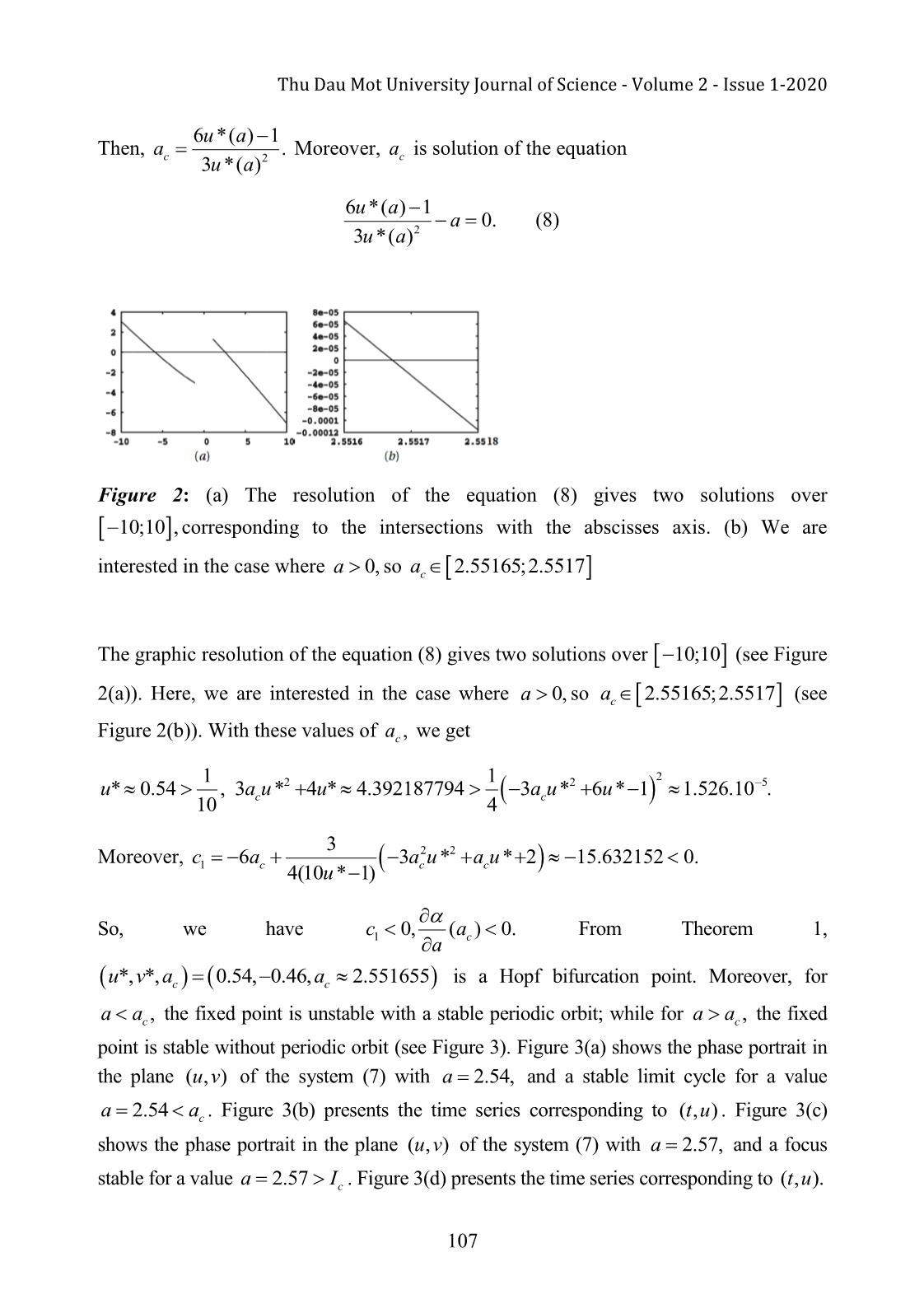
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: A study of fixed points and hopf bifurcation of hindmarshrose model

a pair of complex conjugate eigenvalues cross the complex plane imaginary axis. Moreover, with the suitable assumptions for the dynamical system, a small-amplitude limit cycle branches from the fixed point. Keywords: Hindmarsh-Rose model, fixed point, Hopf bifurcation, limit cycle 1. Introduction In the beginning of 1980s, Hindmarsh J.L. and Rose R.M. studied a model called Hindmarsh-Rose model, to expose part of the inner working mechanism of the Hodgkin- Huxley equations, a famous model in study of neurophysiology since 1952. The Hindmarsh-Rose model was introduced as a dimensional reduction of the well-known Hodgkin-Huxley model (Hodgkin A. L., and Huxley A. F., 1952; Nagumo J., et al., 1962; 98 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 Izhikevich E. M ., 2007; Ermentrout G. B., and Terman D. H ., 2009 ; Keener J. P., and Sney J., 2009 ; Murray J. D., 2010 ). It is constituted by two equations in two variables u and v . The first one is the fast variable called excitatory representing the transmembrane voltage. The second variable is the slow recovery variable describing the time dependence of several physical quantities, such as the electrical conductance of the ion currents across the membrane. The Hindmarsh-Rose equations (HR) are given by du u f(,), u v v au32 bu I dt (1) dv v g(,), u v c du2 v dt where u corresponds to the membrane potential, v corresponds to the slow flux ions through the membrane, I corresponds to the applied extern current, and a,,, b c d are parameters. Here, I,,,, a b c d are real numbers. The paper is organized as follows. In section 2, a study of fixed point is investigated and all necessary conditions for the parameters of Hindmarsh-Rose model are found in order to have a stable focus. In section 3, the system undergoes subcritical Hopf bifurcation is shown. And finally, conclusions are drawn in Section 4. 2. A study of fixed points Equilibria or stability are tools to study the dynamic of fixed points. In mathematics, a fixed point of a function is an element of the function's domain that is mapped to itself by the function. This paper focuses on the fixed points of the system (1) given by the resolution of the following system f( u , v ) 0 v au32 bu I 0 2 g( u , v ) 0 v c du It implies that au32 ( d b ) u c I 0. (2) db cI Let and . The equation (2) can be written a a uu32 0. To solve this equation, let's use the Cardan's formula after the following variables changes: 99 Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. d b( d b )23 2( d b ) c I u ,,, p q then 3 pq 0. 3a 3 a23 27 a a Let now 4pq32 27 . If 0, then the equation (2) admits only one root and hence the system (1) admits a unique fixed point. Now, if 0, then the system (1) admits two fixed points, and finally if 0 , the system (1) admits three fixed points (see Figure 1). The Jacobian matrix of the system (1) is written as the following: f(,)(,) u v f u v uv 3au2 2 bu 1 Au(). g(,)(,) u v g u v 21du uv Let (uv *, *) be one fixed point of (1), we have 2 Det( A ( u *) I2 ) Tr( A ( u *)) Det ( A ( u *)), where Tr( A ( u )) 3 au2 6 u 1 and Det( A ( u )) 3 au2 4 u . The reduced discriminant of Tr( A ( u )) is ' ba2 3 . If ba2 3 , then Tr( A ( u )) admits two real roots given by b b2 3 a b D b b2 3 a b D u and u with D b2 3. a Tr1 33aaTr 2 33aa Two roots of Det( A ( u )) is ()()d b d b 2 db ()()d b d b 2 u 2 and u 0. Det1 33aaDet2 3a The nature of fixed points is rapported in Table 1. TABLE 1: Stability of fixed point If ba2 3, then Tr( A ( u )) 0 for all values of u and in this case, the fixed point is only stable focus or stable node. Morever, in this study, the model is needed to generate the 100 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 potential actions, it is necessary for the existence of a limit cycle. In the other word, it is need to have an unstable focus or a center. So the condition ba2 3 is chosen to be in the region IV of Table 1. The infimum and superimum in the region IV are given by bD bD L and M . 3a 3a To observe the behavior of the system (1) like Figure 1, we fix the values of parameters as the following a 1, b 3, c 1, d 5, I 0. Then, the system (1) becomes du v u32 3 u dt (3) dv 15 uv2 dt The system (3) has three fixed points: ABC ( 1.618033989, 12.090169948), ( 1, 4), (0.618033989, 0.909830058). In Figure 1(a), we simulated two nullclines, u 0 in red and v 0 in green. The intersection point of these two nullclines is three fixed points ABC,, and one orbit of (3) is represented in blue and it is a limit cycle. Figure 1: Numerical results obtained for two nullclines in green and in blue. The intersection points are fixed points A, B and C. The red curve is the limit cycle. At the point A, we get Det( A ) 1.381966013 and Tr( A ) 18.562305903, so A is a stable node. At the point B , we get Det( B ) 1 and Tr( B ) 10, hence B is a 101 Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. saddle. At the point C, we get Det( C ) 3.618033991 and Tr( C ) 1.562305899, so C is a instable focus. 3. existence and direction of hopf bifurcation This section focuses on the existence and the direction of Hopf bifurcation, which corresponds to the passage of a fixed point to a limit cycle under the effect of variation of a parameter. Recall the Hopf's theorem (Dang-Vu Huyen, and Delcarte C., 2000). Theorem 1. Consider the system of two ordinary differential equations u f(,,) u v a (4) v g(,,) u v a Let (uv *, *) a fixed point of the system (4) for all a . If the Jacobian matrix of the system (4) at admits two conjugate complex eigenvalues, 1,2 ()()()a a iw a and there is a certain value aa c such that ()a (a ) 0, w ( a ) 0 and (a ) 0. cc a c Then, a Hopf bifurcation survives when the value of bifurcation parameter a passes by ac and (u *, v *, ac ) is a point of Hopf bifurcation. Moreover, let c1 in order that 1 2FGFFGG 2 2 2 2 2 c1 2 2 2 2 16w ( a ) u u u u v u u v c (5) 2GGFFFGFFGG 2 2 2 2 2 3 3 3 3 2 2 2 2 3 2 2 3 , vuvvuvvv u uvuvv where F and G are given by the method of Hassard, Kazarinoff and Wan (Dang-Vu Huyen, and Delcarte C., 2000). We can distinguish different cases TABLE 2: Stability of the fixed points according to Hopf bifurcation c1 0 c1 0 stable equilibrium stable equilibrium aa c and no periodic orbit and unstable periodic orbit (ac ) 0 a unstable equilibrium unstable equilibrium aa c and stable periodic orbit and no periodic orbit 102 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 unstable equilibrium unstable equilibrium aa c and stable periodic orbit and periodic orbit (ac ) 0 a stable equilibrium stable equilibrium aa c and no periodic orbit and unstable periodic orbit Now this theorem is applied to the Hindmarsh-Rose model in which a represents the bifurcation parameter du v au32 3 u I dt (6) dv 15 uv2 dt Let (uv *, *) a fixed point of the system (6). Let u u1 u* and v v1 v*, then 32 ufuva1 (,,)( 1 1 vv 1 *) auu ( 1 *) 3( uu 1 *) I 2 v1 g(,,)15( u 1 v 1 a u 1 u *) ( v 1 v *) With a development of the functions f and g at the neighborhood of (0,0,a ) , the above systems become ff u1 u 1(0,0,) a v 1 (0,0,) a F (, u 1 v 1 ,) a uv11 gg v u(0,0,) a v (0,0,) a G (, u v ,) a 1 1 1 1 1 uv11 where F(,,) u11 v a and G(,,) u11 v a are the nonlinear terms, then 2 u1 ( 3 au * 6 u *) u 1 v 1 F ( u 1 , v 1 , a ) v1 10 u * u 1 v 1 G ( u 1 , v 1 , a ) 32 2 with F( u1 , v 1 , a ) au 1 ( 3 au * 3) u 1 and G( u1 , v 1 , a ) 5 u 1 . Now, (0,0,a ) is a fixed point of the system. The Jacobian matrix is given by 3au *2 6 u * 1 A . 10u * 1 103 Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. The characteristic polynomial 2 2 2 Det( A I2 ) (3au * 6*1) u 3 au * 4*. u Let P()() a Tr A and Q()() a Det A . We get 2 P( a ) Q ( a ) 0. Hence, the Jacobian matrix admits a pair of conjugate complex eigenvalues if 1 Det()() A Tr A 2 and the above equation has the following roots 4 1,2 (a ) iw ( a ), 3au *2 6 u * 1 with ()a and w( a ) 3 au *22 4 u * ( a ) . 2 Moreover, the value ac of a , for which the real part of these eigenvalues is null, is given by the equations Pa(c ) 0 and Qa(c ) 0 , then 6u * 1 41 a and au *. c 3*u 2 c 3u * 10 3*u 2 Moreover, ().a a c 2 ()I Thus, (a ) 0, w ( a ) 0 and (a ) 0 , then a is a bifurcation Hopf value of cc a c c the parameter a. In the following, the direction and the stability of Hopf bifurcation are investigated. To do this, let’s determine an eigenvector v1 associated with the eigenvalue 1 , obtained by resolving the system u (1 i 10 u * 1) u v 0 (A 1 I2 ) 0 v 10u * u 1 i 10 u * 1 v 0 A solution of this system is an eigenvector associated with given by 1 V1 . 1 iu 10 * 1 The base change matrix is given by 104 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 10 PVV Re(11 ) Im( ) . 1 10u * 1 Then 1 10u * 1 0 P 1 . 10u * 1 11 Now let the variable change u1 u 2 u 2 1 u 1 PP . v1 v 2 v 2 v 1 Hence u u u F(,,) u v a 2 1 1 1 2 1 22 P P AP P . v 2 G(,,) u22 v a vv21 1 ()()a w a Let A'( a ) P AP . Then, for aa c , it implies that w()() a a 0 wa (c ) u2 w()(,,) acc v 2 F u 2 v 2 a Aa'(c ) wa(c ) 0 v2 w()(,,) acc u 2 G u 2 v 2 a with F(,,) u22 v ac 1 F(,,) u22 v ac P . G(,,) u v a 22c G(,,) u22 v ac Then F( u , v , a ) au32 ( 3 au * 3) u 2 2 2 2 1 32 G( u2 , v 2 , a ) au 2 (3 au * 2) u 2 10u * 1 Let c1 be given by the equation (5). The functions F and G depend only on u2 , the coefficient is given by 1 2FGF 2 3 c1 2(0,0, ac ) 2 (0,0, a c ) 3 (0,0, a c ). 16w ( ac ) u2 u 2 u 2 105 Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. At the point (uv22 , ) (0,0) and for aa c , it implies that w( ac ) 10 u * 1 , and 14 c 6 a . 3 a u * 3 3 a u * 2 1 c16 10uu * 1 10 * 1 c c 3 22 6ac 3 a c u * a c u * 2 . 4(10u * 1) Theorem 1 permits to deduce the direction and the stability of Hopf bifurcation from the signs of ()a and c . Now we apply this theorem in fixing all parameters values a c 1 except the bifurcation parmaeter a. Let I 0, the system (6) becomes du v au32 3 u dt (7) dv 15 uv2 dt 21 The fixed points are given by resolving the equation uu32 0. aa Let 2 42 16 1 u ,,, p q 3a 3 a23 27 a a then 3 pq 0. Let now 4pq32 27 . We choose arbitrarily one condition over a, in order to have only a fixed point, it means 4 2 4 2 0 a ; ; . 3 3 3 3 With those values of a, we get 2 9a 27 a22 32 27 3 a 16 3 3 ua*() 11 1 3236 3a 9 a 27 a22 32 27 3 a 16 3 3 1 11 2 1 223 3 6 9a 27 a22 32 27 3 a 16 3 3 42 3 3 3 . 11 1 3.236 3a 9 a 27 a22 32 27 3 a 16 3 3 106 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 6ua *( ) 1 Then, a . Moreover, a is solution of the equation c 3ua *( )2 c 6ua *( ) 1 a 0. (8) 3ua *( )2 Figure 2: (a) The resolution of the equation (8) gives two solutions over 10;10 , corresponding to the intersections with the abscisses axis. (b) We are interested in the case where a 0, so ac 2.55165;2.5517 The graphic resolution of the equation (8) gives two solutions over 10;10 (see Figure 2(a)). Here, we are interested in the case where so ac 2.55165;2.5517 (see Figure 2(b)). With these values of ac , we get 112 22 5 u* 0.54 , 3 acc u * 4 u * 4.392187794 3 a u * 6 u * 1 1.526.10 . 10 4 3 22 Moreover, c1 6 ac 3 a c u * a c u * 2 15.632152 0. 4(10u * 1) So, we have ca 0, ( ) 0. From Theorem 1, 1 a c u*, v *, acc 0.54, 0.46, a 2.551655 is a Hopf bifurcation point. Moreover, for aa c , the fixed point is unstable with a stable periodic orbit; while for aa c , the fixed point is stable without periodic orbit (see Figure 3). Figure 3(a) shows the phase portrait in the plane (,)uv of the system (7) with a 2.54, and a stable limit cycle for a value aa 2.54 c . Figure 3(b) presents the time series corresponding to (,)tu . Figure 3(c) shows the phase portrait in the plane of the system (7) with a 2.57, and a focus stable for a value aI 2.57 c . Figure 3(d) presents the time series corresponding to (tu , ). 107 Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. Figure 3: (a) Phase portrait in the plane (,)uv of the system (7) with a 2.54, and a stable limit cycle for a value aa 2.54 c . (b) Time series corresponding to (,)tu . (c) Phase portrait in the plane of the system (7) with a 2.57, and a focus stable for a value aI 2.57 c . (d) Time series corresponding to 4. Conclusion This work showed the necessary conditions for the parameters of Hindmarsh-Rose model such that there exists only a stable fixed point. It represents the resting state in this system. The parameter a is chosen like a bifurcation parameter, and when it crosses through the bifurcations values, then the equilibrium point loses its stability and becomes a limit cycle that implies the existence of a Hopf bifurcation. In this paper, the Hindmarsh-Rose model has one bifurcation value where there exists the subcritical Hopf bifurcation. The future work will be studied about the chaos properties in the Hindmarsh-Rose by adding some perturbation parameters. References Arena P., Fortuna L., Frasca M., La RosaM., (2006). Locally active Hindmarsh-Rose neurons, Chaos Sol. and Fract. 27:405-412. Dang-Vu Huyen, and Delcarte, C., (2000). Bifurcations and Chaos, an introduction to dynamicscontemporary with programs in Pascal, Fortan et Mathematica. Eds Elipses, Université – Mécanique (in french). 108 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 Ermentrout, G. B., Terman, D. H., (2009). Mathematical Foundations of Neurosciences. Springer. Hodgkin, A.L., and Huxley, A. F., (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117: 500-544. Izhikevich, E. M., (2007). Dynamical Systems in Neuroscience. The MIT Press. Keener, J. P., and Sneyd, J., (2009). Mathematical Physiology. Springer. Murray, J. D., (2010). Mathematical Biology. Springer. Nagumo, J., Arimoto, S., and Yoshizawa, S., (1962). An active pulse transmission line simulating nerve axon. Proc. IRE. 50: 2061-2070. Nikolov S., (2005). An alternative bifurcation analysis of the Rose-Hindmarsh model, Chaos Solitons and Fractal. 23:1643-1649. 109
File đính kèm:
 a_study_of_fixed_points_and_hopf_bifurcation_of_hindmarshros.pdf
a_study_of_fixed_points_and_hopf_bifurcation_of_hindmarshros.pdf

