Bài giảng Toán rời rạc - Chương 7: Quan hệ - Nguyễn Quỳnh Diệp

CHƯƠNG 7
 QUAN HỆ
 Nguyễn Quỳnh Diệp
 diepnq@tlu.edu.vn
 1
 Nguyễn Quỳnh Diệp
NỘI DUNG
 • Quan hệ và các tính chất
 • Quan hệ n-ngôi và những ứng dụng
 • Biểu diễn các quan hệ
 • Bao đóng của các quan hệ
 Toán rời rạc Nguyễn Quỳnh Diệp 2
7.1 QUAN HỆ VÀ CÁC TÍNH CHẤT
 Toán rời rạc Nguyễn Quỳnh Diệp 3
 QUAN HỆ
• Có nhiều quan hệ giữa các phần tử của các tập hợp
• Các mối quan hệ giữa các phần tử được biểu diễn bằng cách dùng 
 một cấu trúc gọi là quan hệ
 Toán rời rạc Nguyễn Quỳnh Diệp 4
QUAN HỆ
 Định nghĩa 1:
 Cho A và B là hai tập hợp. Một quan hệ hai ngôi từ A đến B là một 
 tập con của A×B
 - Quan hệ hai ngôi từ A đến B là tập R các cặp được sắp, phần tử 
 đầu thuộc A, phần tử thứ hai thuộc B
 - Kí hiệu: 푹 để chỉ (a,b) R
 푹 để chỉ (a,b) R
 Toán rời rạc Nguyễn Quỳnh Diệp 5
QUAN HỆ
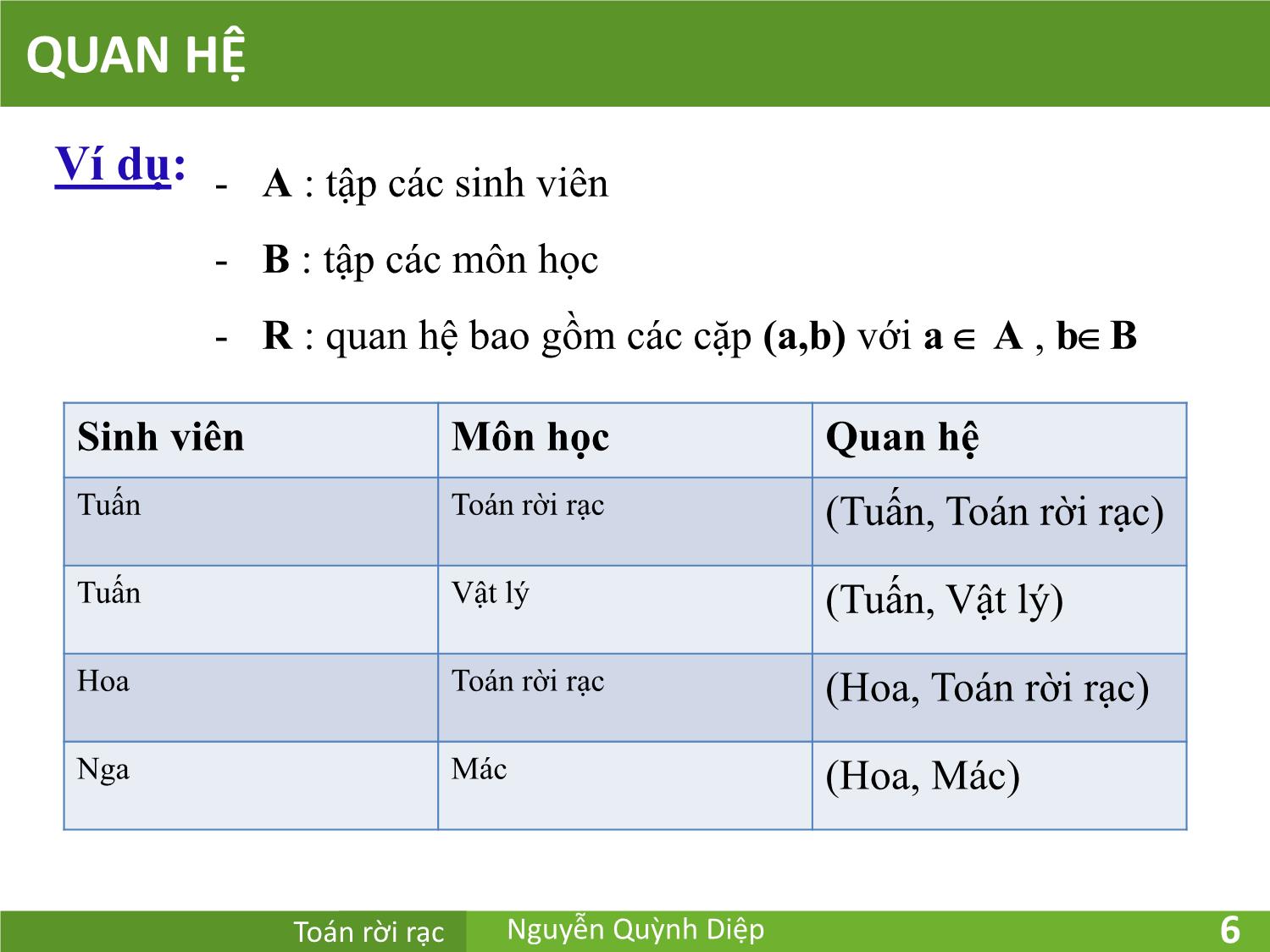
 Ví dụ: - A : tập các sinh viên
 - B : tập các môn học
 - R : quan hệ bao gồm các cặp (a,b) với a A , b B
 Sinh viên Môn học Quan hệ
 Tuấn Toán rời rạc (Tuấn, Toán rời rạc)
 Tuấn Vật lý (Tuấn, Vật lý)
 Hoa Toán rời rạc (Hoa, Toán rời rạc)
 Nga Mác (Hoa, Mác)
 Toán rời rạc Nguyễn Quỳnh Diệp 6
QUAN HỆ
 Định nghĩa 2:
 Một quan hệ trên tập A là quan hệ từ A tới A
 - Quan hệ trên tập A là một tập con của A × A
 Toán rời rạc Nguyễn Quỳnh Diệp 7
QUAN HỆ
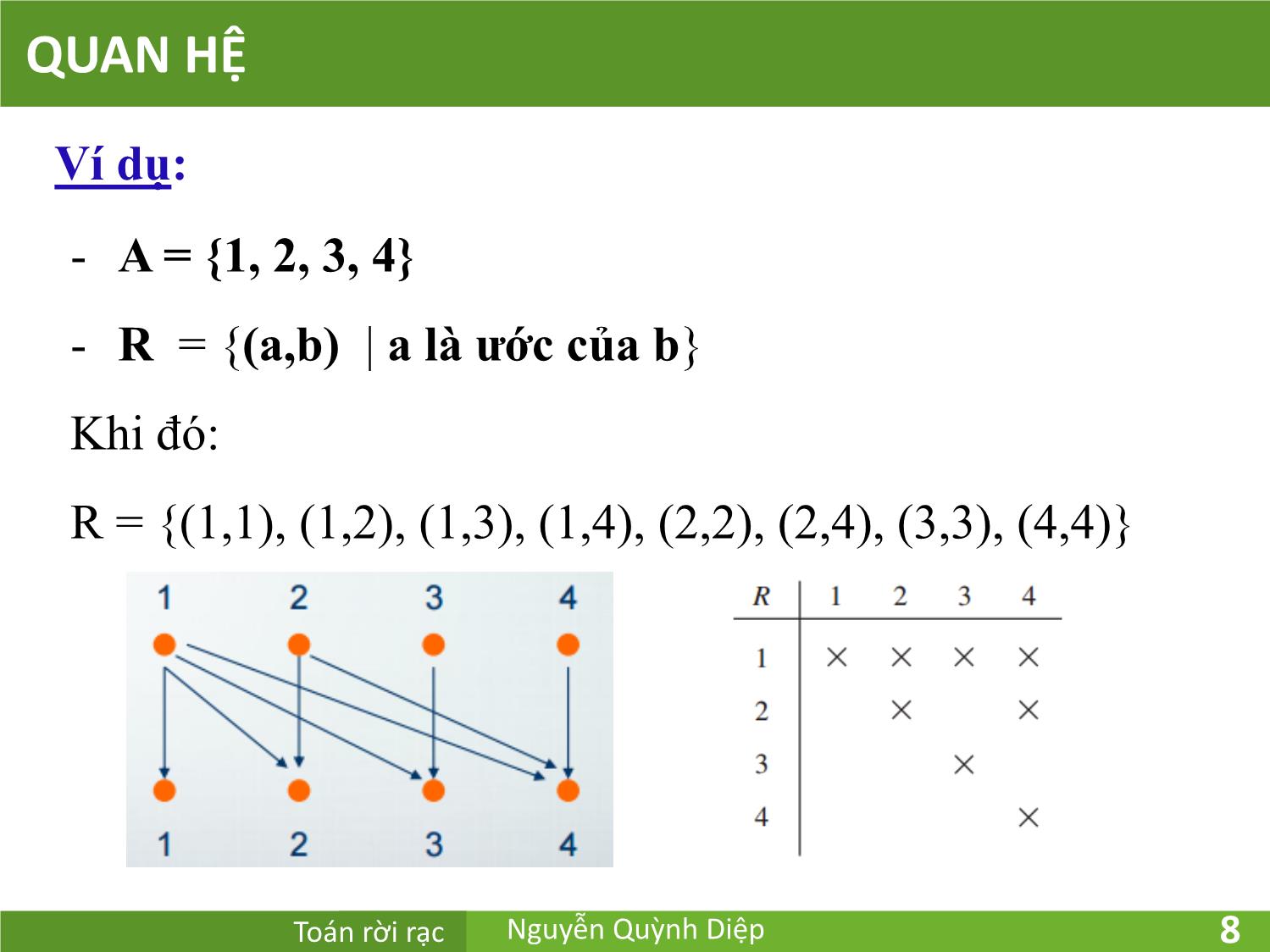
 Ví dụ:
 - A = {1, 2, 3, 4}
 - R = {(a,b) | a là ước của b}
 Khi đó:
 R = {(1,1), (1,2), (1,3), (1,4), (2,2), (2,4), (3,3), (4,4)}
 Toán rời rạc Nguyễn Quỳnh Diệp 8
CÁC TÍNH CHẤT CỦA QUAN HỆ
 Định nghĩa 3:
 Quan hệ R trên tập A được gọi là có tính phản xạ nếu (a,a) R
 Ví dụ: Xét các quan hệ sau trên tập {1, 2, 3, 4}
 quan hệ nào có tính phản xạ?
 Toán rời rạc Nguyễn Quỳnh Diệp 9
CÁC TÍNH CHẤT CỦA QUAN HỆ
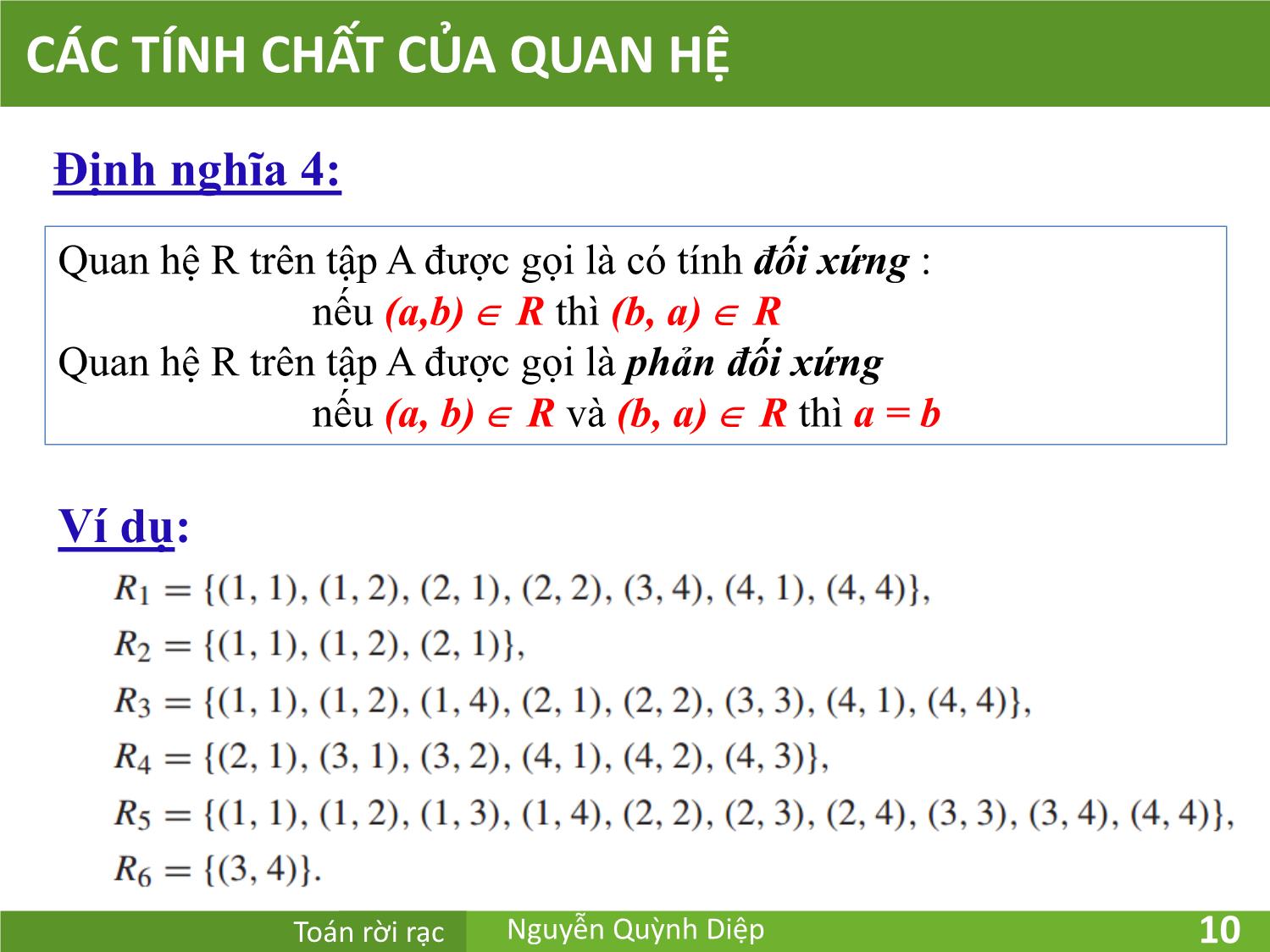
 Định nghĩa 4:
 Quan hệ R trên tập A được gọi là có tính đối xứng :
 nếu (a,b) R thì (b, a) R
 Quan hệ R trên tập A được gọi là phản đối xứng
 nếu (a, b) R và (b, a) R thì a = b
 Ví dụ:
 Toán rời rạc Nguyễn Quỳnh Diệp 10
CÁC TÍNH CHẤT CỦA QUAN HỆ
 Định nghĩa 5:
 Quan hệ R trên tập A được gọi là có tính bắc cầu:
 nếu (a,b) R và (b, c) R thì (a, c) R
 Ví dụ:
 - Quan hệ R = {(2,1) , (3,1) , (3, 2) , (4, 1) , (4, 2) , (4, 3)}
 Trên tập A ={1, 2, 3, 4} có tính bắc cầu
 Toán rời rạc Nguyễn Quỳnh Diệp 11
7.2 QUAN HỆ N-NGÔI VÀ ỨNG DỤNG
 Toán rời rạc Nguyễn Quỳnh Diệp 12
QUAN HỆ n-NGÔI
 Định nghĩa 1:
 Cho A1, A2,  , An là các tập hợp. Một quan hệ n-ngôi trên các tập 
 này là một tập con của A1 × A2  × An
 - A1, A2,  , An gọi là miền của quan hệ
 - n gọi là bậc của quan hệ
 Ví dụ:
 - Quan hệ R gồm bộ 5 (A, N, S, D, T)
 - Trong đó: A: hãng hàng không
 - N: Số chuyến bay 
 - S: nơi xuất phát
 - D: nơi đến
 - T: thời gian xuất phát
 Toán rời rạc Nguyễn Quỳnh Diệp 13
CƠ SỞ DỮ LIỆU
• Một cơ sở dữ liệu gồm các bản ghi như một quan hệ n-ngôi.
 Ví dụ:
 Tên Mã sinh viên Ngành học Điểm trung bình
 Ackermand 2342234 Tin học 3,88
 Adams 8773324 Vật lí 3,45
 Chou 9834532 Tin học 3,49
 Goodfriend 1093434 Toán 3,45
 Rao 7673387 Toán 3,90
 Stevens 9835345 Tâm lí học 2,99
 Toán rời rạc Nguyễn Quỳnh Diệp 14
CÁC PHÉP TOÁN TRÊN QUAN HỆ n-NGÔI
 Phép chọn
 Giả sử R là một quan hệ n-ngôi và C là điều kiện mà các phần tử 
 trong R có thể thỏa mãn. Khi đó phép chọn Sc ánh xạ quan hệ n-
 ngôi R tới quan hệ n-ngôi gồm tất cả các bộ n-thành phần của R 
 thỏa mãn điều kiện C đó.
 Ví dụ:
 Quan hệ nào được tạo thành khi dùng phép chiếu P1,4 lên quan hệ:
 (sinh viên, mã sinh viên, ngành học, điểm trung bình)
 Toán rời rạc Nguyễn Quỳnh Diệp 15
CÁC PHÉP TOÁN TRÊN QUAN HỆ n-NGÔI
 Phép chiếu
 Phép chiếu ánh xạ bộ n-phần tử (a , a ,  , a ) tới bộ 
 푷풊 풊 풊 1 2 n
 m-phần tử ( 풊 , 풊 , 풊 ), trong đó m≤ n
 Ví dụ:
 - Tìm các bản ghi có ngành học là Tin học
 - Sử dụng phép chọn Sc với C là điều kiện
 Ngành học = “Tin học”
 Toán rời rạc Nguyễn Quỳnh Diệp 16
CÁC PHÉP TOÁN TRÊN QUAN HỆ n-NGÔI
 Ví dụ: Hỏi sẽ nhận được bảng nào khi thực hiện phép chiếu P1,2
 tới quan hệ cho trong bảng sau
 Sinh viên Ngành học Môn học
 Glauser Sinh học BI 290
 Glauser Sinh học MS 475
 Glauser Sinh học PY 410
 Marcus Toán MS 511
 Marcus Toán CS 322
 Marcus Toán MS 603
 Miller Tin học MS 575
 Miller Tin học CS 455
 Toán rời rạc Nguyễn Quỳnh Diệp 17
CÁC PHÉP TOÁN TRÊN QUAN HỆ n-NGÔI
 Phép kết nối
 Cho R là một quan hệ bậc m và S là một quan hệ bậc n.
 Phép kết nối Jp(R,S), với p ≤ m và p ≤ n là một quan hệ bậc 
 m+n – p chứa tất cả các bộ (m + n – p) thành phần:
 (a1 , a2 , .. am-p ,c1, c2  cp , b1, b2, bn-p )
 với 
 - (a1 , a2 , .. am-p ,c1, c2  cp) R
 - (c1, c2  cp, b1 , b2 , .. bn-p ) S
 Toán rời rạc Nguyễn Quỳnh Diệp 18
CÁC PHÉP TOÁN TRÊN QUAN HỆ n-NGÔI
 Ví dụ: Hỏi sẽ nhận được bảng nào khi thực hiện phép chiếu kết 
 nối J2 giữa 2 bảng sau
 Bảng QH: Giảng viên_Môn học Bảng: Lịch học_Phòng học
 Giáo sư Khoa Môn học Khoa Môn học Phòng Thời gian
 Toán rời rạc Nguyễn Quỳnh Diệp 19
CÁC PHÉP TOÁN TRÊN QUAN HỆ n-NGÔI
 Bảng quan hệ: Giảng viên_Thời khóa biểu
 Giáo sư Khoa Môn học Phòng Thời gian
 Toán rời rạc Nguyễn Quỳnh Diệp 20
 7.3 BIỂU DIỄN QUAN HỆ
Toán rời rạc Nguyễn Quỳnh Diệp 21
 BIỂU DIỄN BẰNG MA TRẬN
• Quan hệ R có thể biểu diễn bằng ma trận MR = [mij]
 풏ế풖 풊, 풋 ∈ 푹
 풊풋 = ቐ
 풏ế풖 풊, 풋 ∉ 푹
 Ví dụ: Cho A={1, 2, 3}, B ={1,2}
 R là quan hệ từ A đến B (a,b) sao cho a>b
 Toán rời rạc Nguyễn Quỳnh Diệp 22
 BIỂU DIỄN BẰNG ĐỒ THỊ
• Quan hệ R trên tập A được biểu diễn bằng đồ thị có hướng
• Các đỉnh và cạnh là cặp (a, b) R
 Ví dụ: Đồ thị có hướng của quan hệ
 R = { (1,1), (1, 3), (2, 1), (2, 3), (2, 4), (3, 1), (3, 3), (4, 1), 
 (4, 3)} 
 Toán rời rạc Nguyễn Quỳnh Diệp 23
 24
Nguyễn Quỳnh Diệp