Bài giảng Toán rời rạc - Chương 6: Cây - Nguyễn Quỳnh Diệp
CÂY
Toán rời rạc 6
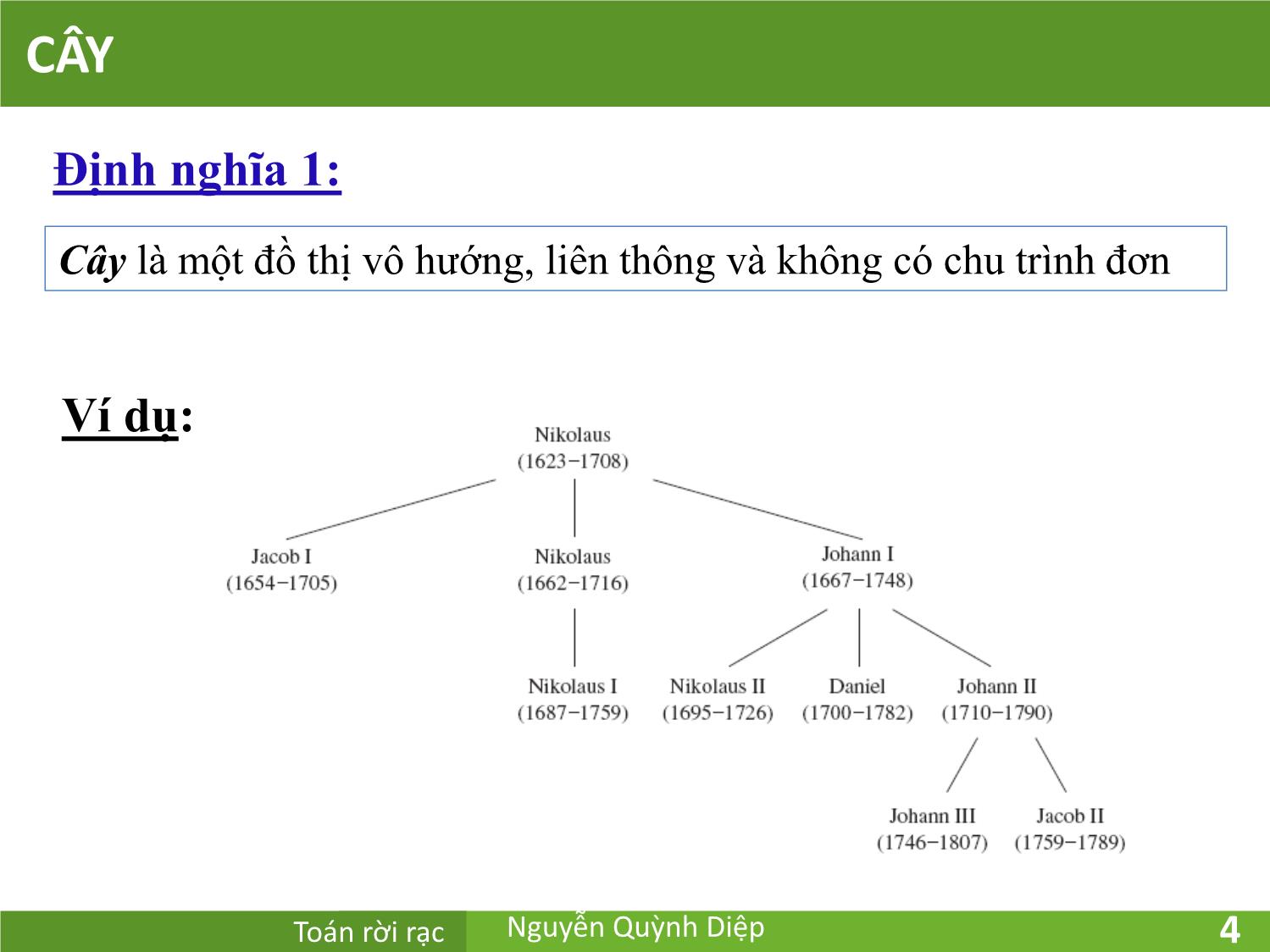
Một đồ thị vô hướng là một cây nếu giữa mọi cặp đỉnh của nó luôn
tồn tại đường đi đơn duy nhất.
Định lí 1:
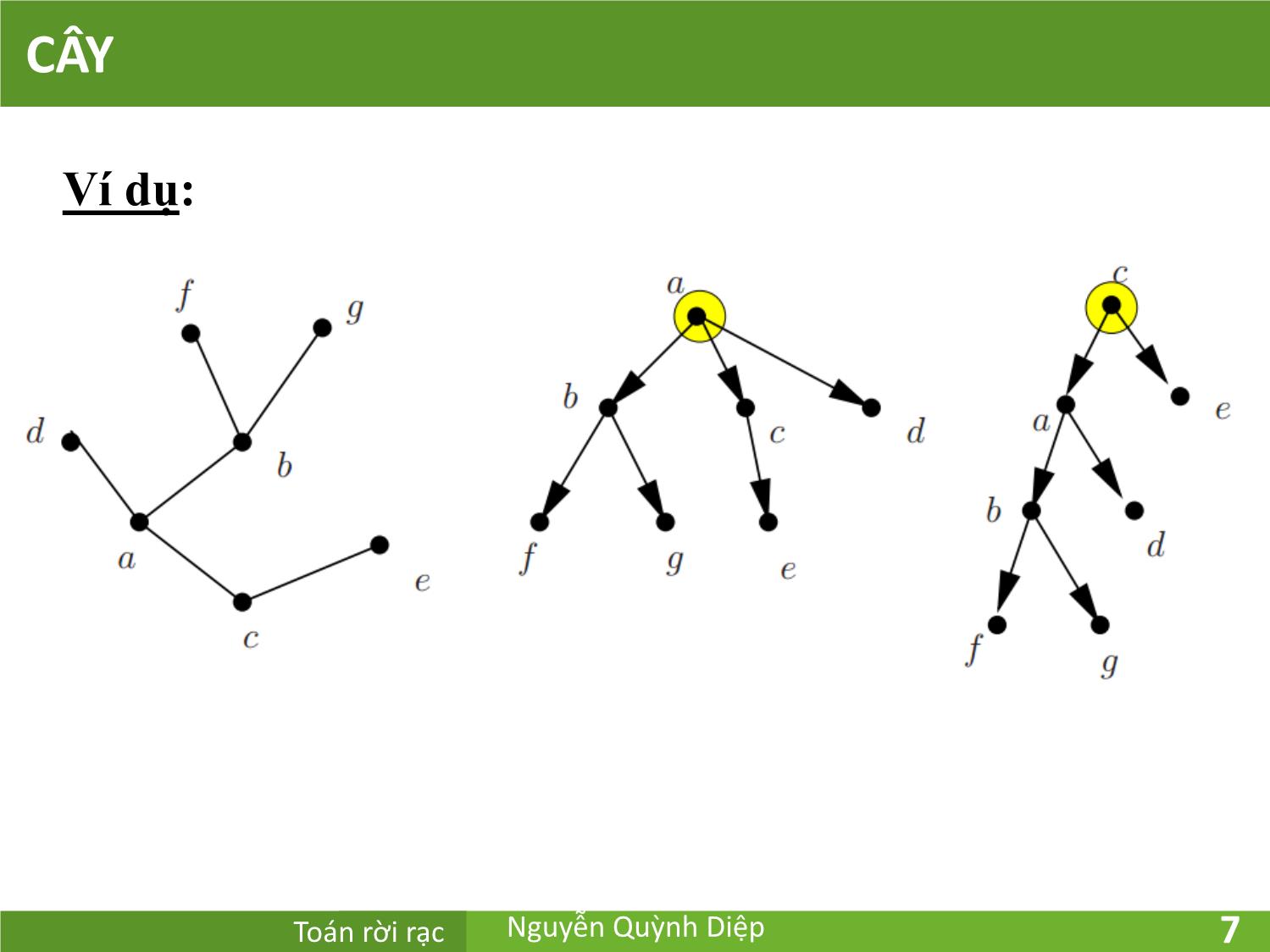
Cây có gốc là cây có một đỉnh được gọi là gốc và mọi cạnh có
hướng từ gốc đi ra

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương 6: Cây - Nguyễn Quỳnh Diệp", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương 6: Cây - Nguyễn Quỳnh Diệp

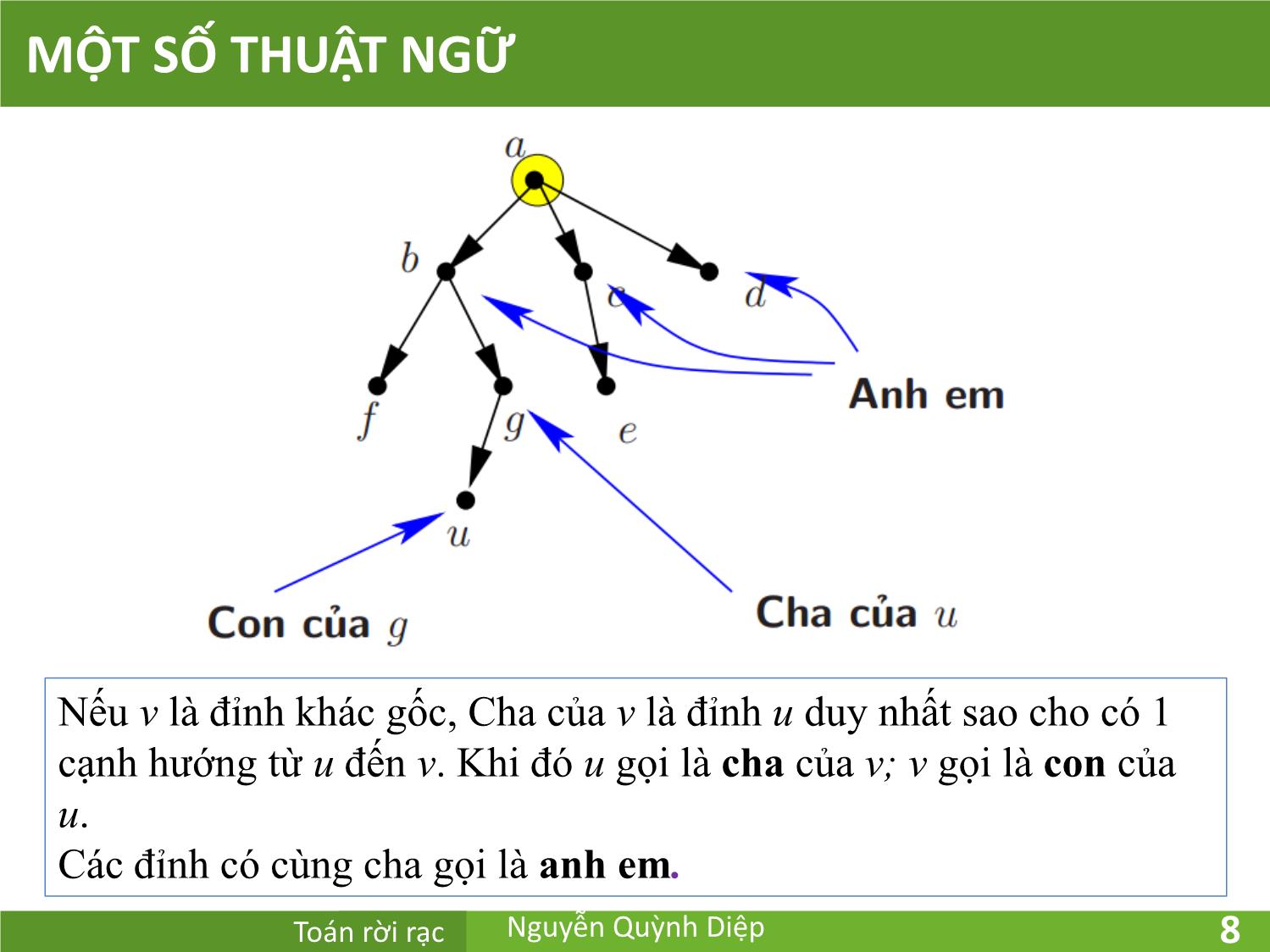
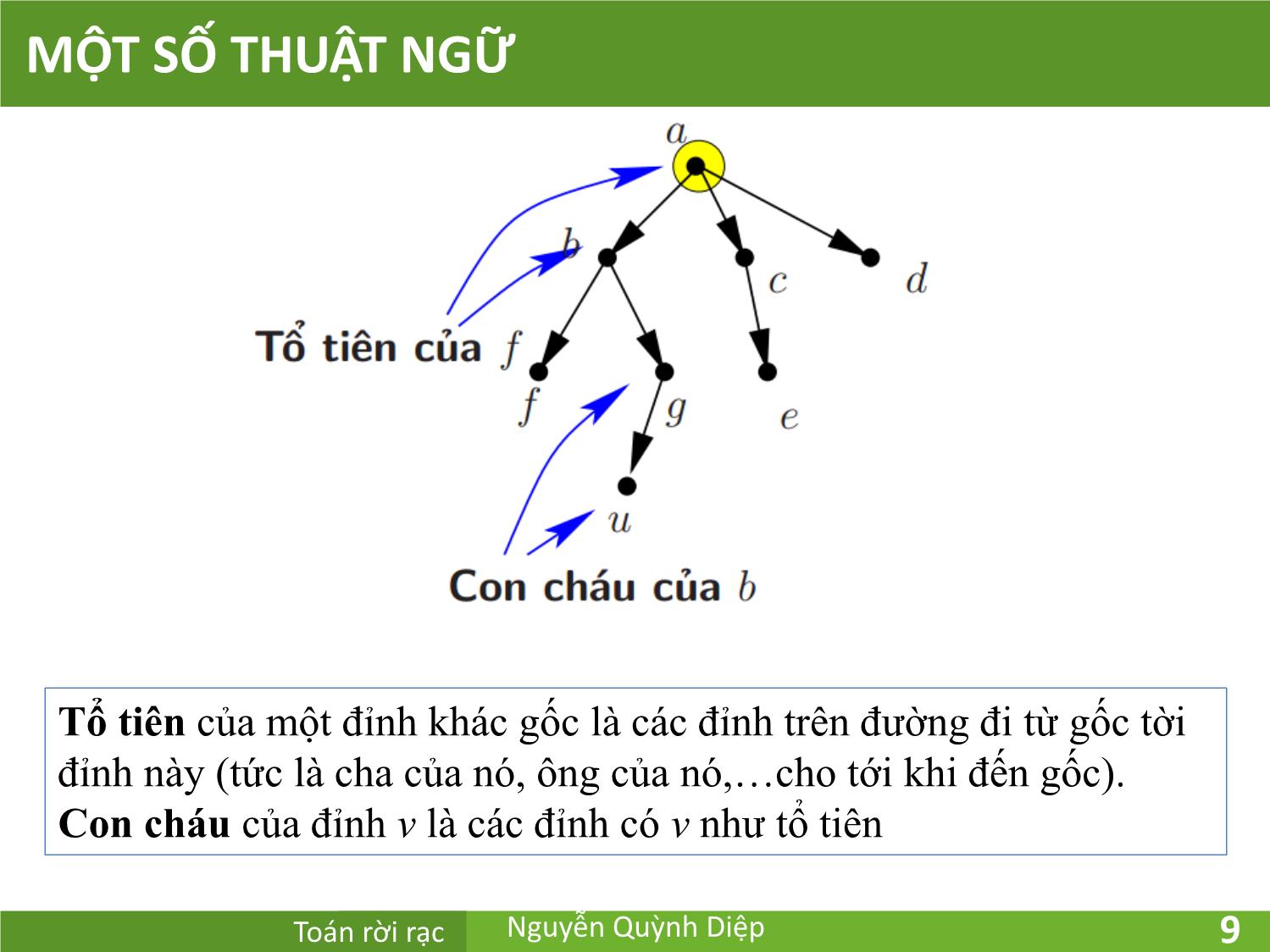
ét, bao gồm a và các con cháu của nó cùng với các cạnh liên
thuộc với các con cháu của a.
Toán rời rạc Nguyễn Quỳnh Diệp 11
CÂY m-phân
Định nghĩa 3:
• Cây có gốc được gọi là cây m-phân nếu tất cả các đỉnh trong của
nó không có hơn m con.
• Cây được gọi là m-phân đầy đủ nếu mọi đỉnh trong có đúng m
con.
• Khi m = 2 ta có cây nhị phân
Toán rời rạc Nguyễn Quỳnh Diệp 12
CÂY CÓ GỐC
Cây có gốc được sắp:
Cây có gốc, được sắp (có thứ tự) là cây có gốc mà trong đó
các con của mỗi đỉnh trong được sắp xếp theo một thứ tự nhất
định.
Toán rời rạc Nguyễn Quỳnh Diệp 13
VÍ DỤ VỀ CÂY
Tổ chức trong công ty
Toán rời rạc Nguyễn Quỳnh Diệp 14
VÍ DỤ VỀ CÂY
Cấu trúc thư mục
Toán rời rạc Nguyễn Quỳnh Diệp 15
CÁC TÍNH CHẤT CỦA CÂY
Định lí 2:
Cây với n đỉnh có đúng (n-1) cạnh
Định lí 3:
Cây m-phân đầy đủ với i đỉnh trong sẽ có tất cả n = m.i + 1 đỉnh.
Toán rời rạc Nguyễn Quỳnh Diệp 16
CÁC TÍNH CHẤT CỦA CÂY
Định lí 4:
Cây m-phân đầy đủ với
풏− − 풏+
(i) n đỉnh có 풊 = đỉnh trong và 풍 = lá
(ii) i đỉnh trong, có n= m.i + 1 đỉnh và l = (m – 1) .i +1 lá
풍 − 풍 −
(iii) l lá, có 풏 = đỉnh và 풊 = đỉnh trong
− −
Toán rời rạc Nguyễn Quỳnh Diệp 17
CÁC TÍNH CHẤT CỦA CÂY
Ví dụ:
Trò chơi viết thư dây chuyền. Ban đầu có một người nhận được một
bức thư và giả sử rằng khi nhận được một bức thư hoặc sẽ viết thư
cho bốn người khác hoặc không viết cho ai. Hỏi có bao nhiêu
người nhận được thư kể cả người đầu tiên nếu không có ai nhận
được nhiều hơn một bức và trò chơi kết thúc khi có 100 người nhận
thư mà ko viết cho ai?
Giải:
• Trò chơi biểu diễn bằng cây tứ phân.
• Có 100 không viết thư nên số lá của cây là l = 100
• Số người nhận thư là n = (4.100 -1 )/(4-1) = 133
• Số các đỉnh trong là i = (100-1)/(4-1) = 33 đỉnh, tức 33 người
viết thư
Toán rời rạc Nguyễn Quỳnh Diệp 18
CÁC TÍNH CHẤT CỦA CÂY
• Mức của đỉnh v trong cây là độ dài của đường đi duy nhất
từ gốc tới nó. Gốc có mức 0
• Độ cao của cây là mức cao nhất của tất cả các đỉnh
• Cây m-phân có độ cao h được gọi là cân đối nếu tất cả các
lá đều ở mức h và (h-1)
Toán rời rạc Nguyễn Quỳnh Diệp 19
CÁC TÍNH CHẤT CỦA CÂY
Định lí 5:
Có nhiều nhất mh lá trong cây m-phân với độ cao h
Toán rời rạc Nguyễn Quỳnh Diệp 20
6.2. CÁC ỨNG DỤNG CỦA CÂY
Toán rời rạc Nguyễn Quỳnh Diệp 21
CÁC ỨNG DỤNG CỦA CÂY
• Cây tìm kiếm nhị phân
• Cây quyết định
• Các mã tiền tố
Toán rời rạc Nguyễn Quỳnh Diệp 22
TÌM KIẾM NHỊ PHÂN
Cây nhị phân:
• Là cây có một cây con trái và một cây con phải
• Mỗi đỉnh được gán một nhãn sao cho:
• Lớn hơn nhãn của tất cả các đỉnh thuộc cây con trái của nó
• Nhỏ hơn nhãn của tất cả các đỉnh thuộc cây con bên phải của
nó
Toán rời rạc Nguyễn Quỳnh Diệp 23
TÌM KIẾM NHỊ PHÂN
Xây dựng cây tìm kiếm nhị phân:
• Bắt đầu cây có đúng 1 đỉnh (gốc)
• Thêm một phần tử mới:
So sánh với nhãn của đỉnh, bắt đầu từ gốc
Đi sang trái nếu nó nhỏ hơn
Đi sang phải nếu nó lớn hơn
Tạo đỉnh mới là con bên trái nếu phần tử nhỏ hơn nhãn của
đỉnh và đỉnh không có con trái
Tạo đỉnh mới là con bên phải nếu phần tử lớn hơn nhãn của
đỉnh và đỉnh không có con phải
Toán rời rạc Nguyễn Quỳnh Diệp 24
TÌM KIẾM NHỊ PHÂN
Ví dụ: Tạo cây tìm kiếm nhị phân cho các từ sau: mathematics,
physics,geography, zoology, meteology, geology, psychology, chemistry
Zoology > Mathemetics
Physics > Mathemetics Geography Physics
Meteorology > Mathemetics Geology Mathemetics
Chemistry < Mathemetics
Meteorology Geography Psychology > Physics
Chemistry < Geography
Psychology < Zoology
Toán rời rạc Nguyễn Quỳnh Diệp 25
TÌM KIẾM NHỊ PHÂN
Thuật toán tìm kiếm nhị phân:
• Định vị phần tử x trong cây tìm kiếm nhị phân nếu nó là
nhãn của một đỉnh
• Nếu x không là nhãn của đỉnh nào, thêm mới x vào cây
Toán rời rạc Nguyễn Quỳnh Diệp 26
TÌM KIẾM NHỊ PHÂN
THUẬT TOÁN : Thuật toán tìm kiếm nhị phân
Procedure insertion(T: cây tìm kiếm nhị phân, x: phần tử)
v := gốc của T { đỉnh không có trong T sẽ có giá trị bằng null }
while v null và label(v) x
begin
if x < label(v) then
if con bên trái của v null then v := con bên trái của v
else thêm đỉnh mới là con trái của v và đặt v := null
else
if con bên phải của v null then v := con bên phải của v
else thêm đỉnh mới là con phải của v và đặt v := null
end
if gốc của T = null then thêm đỉnh v vào cây và gán cho nó nhãn là x
else if v = null hoặc label(v) x then gán nhãn cho đỉnh mới là x và đặt v là
đỉnh mới này
{ v = vị trí của x }
Toán rời rạc Nguyễn Quỳnh Diệp 27
6.3. CÁC PHƯƠNG PHÁP DUYỆT CÂY
Toán rời rạc Nguyễn Quỳnh Diệp 28
CÁC PHƯƠNG PHÁP DUYỆT CÂY
• Duyệt tiền thứ tự (thứ tự trước)
• Duyệt trung thứ tự (thứ tự giữa)
• Duyệt hậu thứ tự (thứ tự sau)
Toán rời rạc Nguyễn Quỳnh Diệp 29
DUYỆT TIỀN THỨ TỰ
Định nghĩa 1:
Giả sử T là một cây được sắp thứ tự với gốc r.
Nếu T chỉ có nút gốc thì r là duyệt tiền thứ tự của cây T.
Ngược lại, thì gọi T1 , T2 , Tn là các cây con của T từ trái qua
phải. Duyệt tiền thứ tự là:
• Thăm r
• Duyệt T1 theo kiểu tiền thứ tự
• Duyệt T2 theo kiểu tiền thứ tự
• ..
• Duyệt Tn theo kiểu tiền thứ tự
Toán rời rạc Nguyễn Quỳnh Diệp 30
DUYỆT TIỀN THỨ TỰ
Ví dụ: Cách duyệt tiền thứ tự sẽ thăm các đỉnh của cây
theo thứ tự nào?
Toán rời rạc Nguyễn Quỳnh Diệp 31
DUYỆT TIỀN THỨ TỰ
THUẬT TOÁN : Duyệt kiểu tiền thứ tự
Procedure Preorder (T: cây có gốc được sắp)
r := gốc của T
Liệt kê r
for mỗi cây con c của r từ trái sang phải
begin
T(c) := cây con với gốc c
Preorder(T(c))
end
Toán rời rạc Nguyễn Quỳnh Diệp 32
DUYỆT TRUNG THỨ TỰ
Định nghĩa 2:
Giả sử T là một cây được sắp thứ tự với gốc r.
Nếu T chỉ có nút gốc thì r là duyệt trung thứ tự của cây T.
Ngược lại, thì gọi T1 , T2 , Tn là các cây con của T từ trái qua
phải. Duyệt trung thứ tự là:
• Duyệt T1 theo kiểu trung thứ tự
• Thăm r
• Duyệt T2 theo kiểu trung thứ tự
• ..
• Duyệt Tn theo kiểu trung thứ tự
Toán rời rạc Nguyễn Quỳnh Diệp 33
DUYỆT TRUNG THỨ TỰ
Ví dụ: Cách duyệt trung thứ tự sẽ thăm các đỉnh của
cây theo thứ tự nào?
Toán rời rạc Nguyễn Quỳnh Diệp 34
DUYỆT TRUNG THỨ TỰ
THUẬT TOÁN : Duyệt kiểu trung thứ tự
Procedure Inorder (T: cây có gốc được sắp)
r := gốc của T
if r là lá then liệt kê r
else
begin
l := con đầu tiên từ trái sang phải của r
T(l) := cây con với gốc l
Inorder(T(l))
Liệt kê r
for mỗi cây con c của r từ trái sang phải trừ l
T(c) := cây con với gốc c
Inorder(T(c))
end
Toán rời rạc Nguyễn Quỳnh Diệp 35
DUYỆT HẬU THỨ TỰ
Định nghĩa 3:
Giả sử T là một cây được sắp thứ tự với gốc r.
Nếu T chỉ có nút gốc thì r là duyệt trung thứ tự của cây T.
Ngược lại, thì gọi T1 , T2 , Tn là các cây con của T từ trái qua
phải. Duyệt hậu thứ tự là:
• Duyệt T1 theo kiểu hậu thứ tự
• Duyệt T2 theo kiểu hậu thứ tự
• ..
• Duyệt Tn theo kiểu hậu thứ tự
• Thăm r
Toán rời rạc Nguyễn Quỳnh Diệp 36
DUYỆT TRUNG THỨ TỰ
Ví dụ: Cách duyệt hậu thứ tự sẽ thăm các đỉnh của cây theo
thứ tự nào?
Toán rời rạc Nguyễn Quỳnh Diệp 37
DUYỆT HẬU THỨ TỰ
THUẬT TOÁN : Duyệt kiểu hậu thứ tự
Procedure Postorder (T: cây có gốc được sắp)
r := gốc của T
for mỗi cây con c của r từ trái sang phải
begin
T(c) := cây con với gốc c
Postorder(T(c))
end
Liệt kê r
Toán rời rạc Nguyễn Quỳnh Diệp 38
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
• Có thể dùng để biểu diễn biểu thức phức tạp:
• Mệnh đề phức hợp
• Tập hợp
• Biểu thức số học
• Biểu diễn bằng cây có gốc và được sắp, trong đó:
• đỉnh trong biểu thị các phép toán
• lá biểu thị các số hay các biến
Toán rời rạc Nguyễn Quỳnh Diệp 39
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
Ví dụ: Tìm cây có gốc biểu diễn biểu thức
풙 − ퟒ
풙 + 풚 ↑ + ( )
Biểu thức có đầy đủ dấu ngoặc đơn gọi là dạng trung tố
Toán rời rạc Nguyễn Quỳnh Diệp 40
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
• Biểu thức được viết dưới dạng tiền tố gọi là kí pháp Ba
Lan
• Khi duyệt biểu thức dạng tiền tố, ta làm như sau:
• Đi từ phải sang trái
• Gặp một toán tử thực hiện phép toán tương ứng với hai toán
hạng đi liền bên phải của toán tử
Ví dụ 1: Tính giá trị biểu thức tiền tố
+ - * 2 3 5 / ↑ 2 3 4
Toán rời rạc Nguyễn Quỳnh Diệp 41
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
• Biểu thức được viết dưới dạng hậu tố gọi là kí pháp Ba
Lan ngược
• Khi duyệt biểu thức dạng hậu tố, ta làm như sau:
• Đi từ trái sang phải
• Thực hiện phép toán khi có một toán tử đi sau hai toán hạng
Ví dụ 2: Tính giá trị biểu thức hậu tố
7 8 + 2 ↑ 7 4 – 3 / +
Toán rời rạc Nguyễn Quỳnh Diệp 42
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
Ví dụ 3:
a). Hãy biểu diễn biểu thức ((x+2)^3)*((y-(3+x))-5) bằng cây nhị
phân.
b). Hãy viết thứ tự duyệt cây dưới dạng: tiền tố, hậu tố, trung tố
Toán rời rạc Nguyễn Quỳnh Diệp 43
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
Ví dụ 4:
Hãy vẽ cây ứng với
a. + * + - 5 3 2 1 4
b. ^ + 2 3 – 5 1
c. * / 9 3 + * 2 4 – 7 6
Toán rời rạc Nguyễn Quỳnh Diệp 44
CÁC KÍ PHÁP TRUNG TỐ, TIỀN TỐ VÀ HẬU TỐ
Ví dụ 5: Hãy tính giá trị các biểu thức sau
a. 5 2 1 - - 3 1 4 + + *
b. + - ^ 3 2 ^ 2 3 / 6 – 4 2
c. 9 3 / 5 + 7 2 - *
d. * + 3 + 3 ^ 3 + 3 3 3
e. 3 2 * 2 ^ 5 3 – 8 4 / * -
Toán rời rạc Nguyễn Quỳnh Diệp 45
6.4. CÂY KHUNG
Toán rời rạc Nguyễn Quỳnh Diệp 46
CÂY KHUNG
Bài toán giao thông ở Maine:
• Chính quyền địa phương muốn cào tuyết một số ít nhất các con
đường sao cho luôn luôn có đường thông suốt nối hai thành phố
bất kì
Toán rời rạc Nguyễn Quỳnh Diệp 47
CÂY KHUNG
Định nghĩa 1:
Cho G là một đơn đồ thị.
Một cây được gọi là cây khung của G nếu nó là một đồ thị
con của G và chứa tất cả các đỉnh của G.
Các cách tìm cây khung của đồ thị:
Xóa đi các cạnh tạo ra chu trình
Bằng phương pháp tìm kiếm theo chiều sâu
Bằng phương pháp tìm kiếm theo chiều rộng
Toán rời rạc Nguyễn Quỳnh Diệp 48
XÓA CÁC CẠNH TẠO CHU TRÌNH
Toán rời rạc Nguyễn Quỳnh Diệp 49
TÌM KIẾM THEO CHIỀU SÂU
• Chọn tùy ý 1 đỉnh của đồ thị làm gốc
• Xây dựng đường đi từ đỉnh này bằng cách ghép nối tiếp các
cạnh vào đường đi, cho đến khi không thể ghép được nữa.
• Nếu đường đi chưa đi qua tất cả các đỉnh thì lùi lại một
bước và xây dựng đường đi mới qua các đỉnh chưa thuộc
đường đi.
• Tiếp tục lùi lại cho đến khi không thực hiện được nữa
Tìm kiếm ưu tiên chiều sâu cũng được gọi là thủ tục quay lui
Toán rời rạc Nguyễn Quỳnh Diệp 50
TÌM KIẾM THEO CHIỀU SÂU
THUẬT TOÁN : Tìm kiếm theo chiều sâu
Procedure DFS(G: đồ thị liên thông với các đỉnh v1 , v2 vn)
T := cây chỉ chứa một đỉnh v1
Visit(v1)
Procedure Visit(v: đỉnh của G)
for mỗi đỉnh w liền kề với v và chưa có trong T
begin
thêm đỉnh w và cạnh (v, w) vào T
Visit(w)
end
Toán rời rạc Nguyễn Quỳnh Diệp 51
TÌM KIẾM THEO CHIỀU SÂU
Ví dụ: Bắt đầu từ đỉnh f
Toán rời rạc Nguyễn Quỳnh Diệp 52
TÌM KIẾM THEO CHIỀU RỘNG
• Chọn tùy ý một đỉnh của đồ thị làm gốc
• Ghép vào tất cả các cạnh liên thuộc với đỉnh này. Đỉnh
ghép vào là đỉnh mức 1 của cây khung
• Với mỗi đỉnh mức 1, ghép tất cả các cạnh liên thuộc với
nó vào cây mà không tạo ra chu trình, ta được các đỉnh
mức 2.
• Tiếp tục cho đến khi tất cả các đỉnh được ghép vào cây
Toán rời rạc Nguyễn Quỳnh Diệp 53
TÌM KIẾM THEO CHIỀU RỘNG
Ví dụ: Dùng thuật toán tìm kiếm theo chiều rộng, tìm cây
khung của đồ thị với đỉnh xuất phát là e
Toán rời rạc Nguyễn Quỳnh Diệp 54
TÌM KIẾM THEO CHIỀU RỘNG
THUẬT TOÁN : Tìm kiếm theo chiều rộng
Procedure BFS(G: đồ thị liên thông với các đỉnh v1 , v2 vn)
T := cây chỉ chứa một đỉnh v1
L := danh sách rỗng
Đặt v1 vào danh sách L gồm các đỉnh không xử lí
while L khác rỗng
begin
Xóa đỉnh đầu tiên, v, khỏi L
for mỗi đỉnh liền kề w của v
if w chưa nằm trong L và không thuộc T then
begin
thêm đỉnh w vào cuối danh sách L
thêm w và cạnh {v, w} vào T
end
end
Toán rời rạc Nguyễn Quỳnh Diệp 55
BÀI TẬP
. Bài 1: Tìm cây khung của đồ thị bằng cách xóa đi các cạnh
56
Toán rời rạc Nguyễn Quỳnh Diệp 56
BÀI TẬP
. Bài 2: Tìm cây khung của đồ thị bằng kĩ thuật tìm kiếm theo
chiều sâu. Chọn a làm gốc của cây.
57
Toán rời rạc Nguyễn Quỳnh Diệp 57
6.5. CÂY KHUNG NHỎ NHẤT
Toán rời rạc Nguyễn Quỳnh Diệp 58
CÂY KHUNG NHỎ NHẤT
Định nghĩa 1:
Cây khung nhỏ nhất trong một đồ thị liên thông có trọng số là một
cây khung có tổng trọng số trên các cạnh của nó là nhỏ nhất
Toán rời rạc Nguyễn Quỳnh Diệp 59
CÂY KHUNG NHỎ NHẤT
Thuật toán tìm cây khung nhỏ nhất:
Thuật toán Prim
Thuật toán Kruskal
Toán rời rạc Nguyễn Quỳnh Diệp 60
THUẬT TOÁN PRIM
• Do Robert Prim đưa ra năm 1957
• Thuật toán:
Chọn một cạnh bất kì có trọng số nhỏ nhất, đặt vào
khung
Ghép vào cây các cạnh có trọng số nhỏ nhất, liên thuộc
với 1 đỉnh của cây và không tạo ra chu trình
Dừng khi có (n-1) cạnh được ghép vào cây
Toán rời rạc Nguyễn Quỳnh Diệp 61
THUẬT TOÁN PRIM
Ví dụ: Tìm cây khung nhỏ nhất
Lần chọn Cạnh Trọng số
Tổng cộng : 24
Toán rời rạc Nguyễn Quỳnh Diệp 62
THUẬT TOÁN PRIM
THUẬT TOÁN : Thuật toán Prim
Procedure Prim(G: đồ thị liên thông có trọng số với n đỉnh)
T := cạnh có trọng số nhỏ nhất
for i:= 1 to n-2
begin
e := cạnh có trọng số tối thiểu, liên thuộc với một đỉnh trong
T và không tạo ra chu trình trong T nếu ghép nó vào T
T := T với e được ghép vào
end
{ T là cây khung nhỏ nhất của G }
Toán rời rạc Nguyễn Quỳnh Diệp 63
THUẬT TOÁN PRIM
Ví dụ: Tìm cây khung nhỏ nhất
4
a b
2
3
3 e
1
1
d c
2
Toán rời rạc Nguyễn Quỳnh Diệp 64
THUẬT TOÁN PRIM
• Cây khung nhỏ nhất gồm các cạnh: {E, C} ; {E, D}; {E, B} ;
{D, A}
• Tổng trọng số nhỏ nhất của cây khung là: 7
4
a b
2
3
3 e
1
1
d c
2
Toán rời rạc Nguyễn Quỳnh Diệp 65
THUẬT TOÁN KRUSKAL
• Do Joseph Kruskal đưa ra năm 1956
• Thuật toán:
Chọn một cạnh bất kỳ có trọng số nhỏ nhất, đặt vào
khung
Ghép vào cây các cạnh có trọng số nhỏ nhất và không
tạo ra chu trình
Dừng khi có (n-1) cạnh được ghép vào cây
Toán rời rạc Nguyễn Quỳnh Diệp 66
THUẬT TOÁN KRUSKAL
THUẬT TOÁN : Thuật toán Kruskal
Procedure Kruskal(G: đồ thị n đỉnh, liên thông, có trọng số)
T := đồ thị rỗng
for i:= 1 to n-1
begin
e := cạnh bất kì của G với trọng số nhỏ nhất và không tạo ra
chu trình trong T khi ghép vào T
T := T với e được ghép vào
end
{ T là cây khung nhỏ nhất của G }
Toán rời rạc Nguyễn Quỳnh Diệp 67
THUẬT TOÁN KRUSKAL
Ví dụ: Tìm cây khung nhỏ nhất
Lần chọn Cạnh Trọng số
Tổng cộng : 24
Toán rời rạc Nguyễn Quỳnh Diệp 68
THUẬT TOÁN PRIM
Ví dụ: Tìm cây khung nhỏ nhất
4
a b
2
3
3 e
1
1
d c
2
Toán rời rạc Nguyễn Quỳnh Diệp 69
BÀI TẬP
. Bài 2: Tìm cây khung nhỏ nhất dùng thuật toán Prim và Kruskal
70
Toán rời rạc Nguyễn Quỳnh Diệp 70
BÀI TẬP
. Bài 2: Tìm cây khung nhỏ nhất dùng thuật toán Prim và Kruskal
71
Toán rời rạc Nguyễn Quỳnh Diệp 71
72
Nguyễn Quỳnh DiệpFile đính kèm:
 bai_giang_toan_roi_rac_chuong_6_cay_nguyen_quynh_diep.pdf
bai_giang_toan_roi_rac_chuong_6_cay_nguyen_quynh_diep.pdf

