Bài giảng Toán rời rạc - Chương 2: Hàm và thuật toán - Nguyễn Quỳnh Diệp

 CHƯƠNG 2
HÀM VÀ THUẬT TOÁN
 Nguyễn Quỳnh Diệp
 diepnq@tlu.edu.vn
 File Bài giảng: goo.gl/Y3cpLF hoặc goo.gl/TYxXQD
 1
 Nguyễn Quỳnh Diệp
NỘI DUNG
 • Hàm
 • Độ tăng của hàm
 • Thuật toán
 • Độ phức tạp của thuật toán
 Toán rời rạc Nguyễn Quỳnh Diệp 2
 2.1. HÀM
Toán rời rạc Nguyễn Quỳnh Diệp 3
HÀM
 • Dùng để định nghĩa các cấu trúc rời rạc như dãy, xâu
 • Dùng để biểu diễn thời gian một máy tính phải mất để 
 giải một bài toán
 Toán rời rạc Nguyễn Quỳnh Diệp 4
HÀM
 Định nghĩa 1:
 Cho A và B là hai tập hợp. Một hàm f từ A đến B là sự gán chính 
 xác một phần tử của B cho mỗi phần tử của A. Ta viết 풇 = 
 nếu b là phần tử duy nhất của B được gán bởi hàm f cho phần tử a
 của A. Nếu f là hàm từ A đến B ta viết: 풇: → .
 Toán rời rạc Nguyễn Quỳnh Diệp 5
HÀM
 Định nghĩa 2:
 Nếu f là một hàm từ A đến B.
 • A được gọi là miền xác định của f và B là miền giá trị của f.
 • Nếu f(a) = b, b gọi là ảnh của a và a là một nghịch ảnh của b.
 • Tập ánh xạ qua hàm f là tập các ảnh của các phần tử thuộc A
 • f ánh xạ A đến B
 Ví dụ: Cho A= {1, 2, 3}, B ={a, b, c}
 • Hàm f được định nghĩa: 1 → , 2 → , 3 → 
 • 1 → , c là ảnh của 1
 • 2 → , 2 là nghịch ảnh của a
 • Miền xác định của f {1, 2, 3}, miền giá trị của f {a, b, c}
 • Tập ánh xạ f {a, c}
 Toán rời rạc Nguyễn Quỳnh Diệp 6
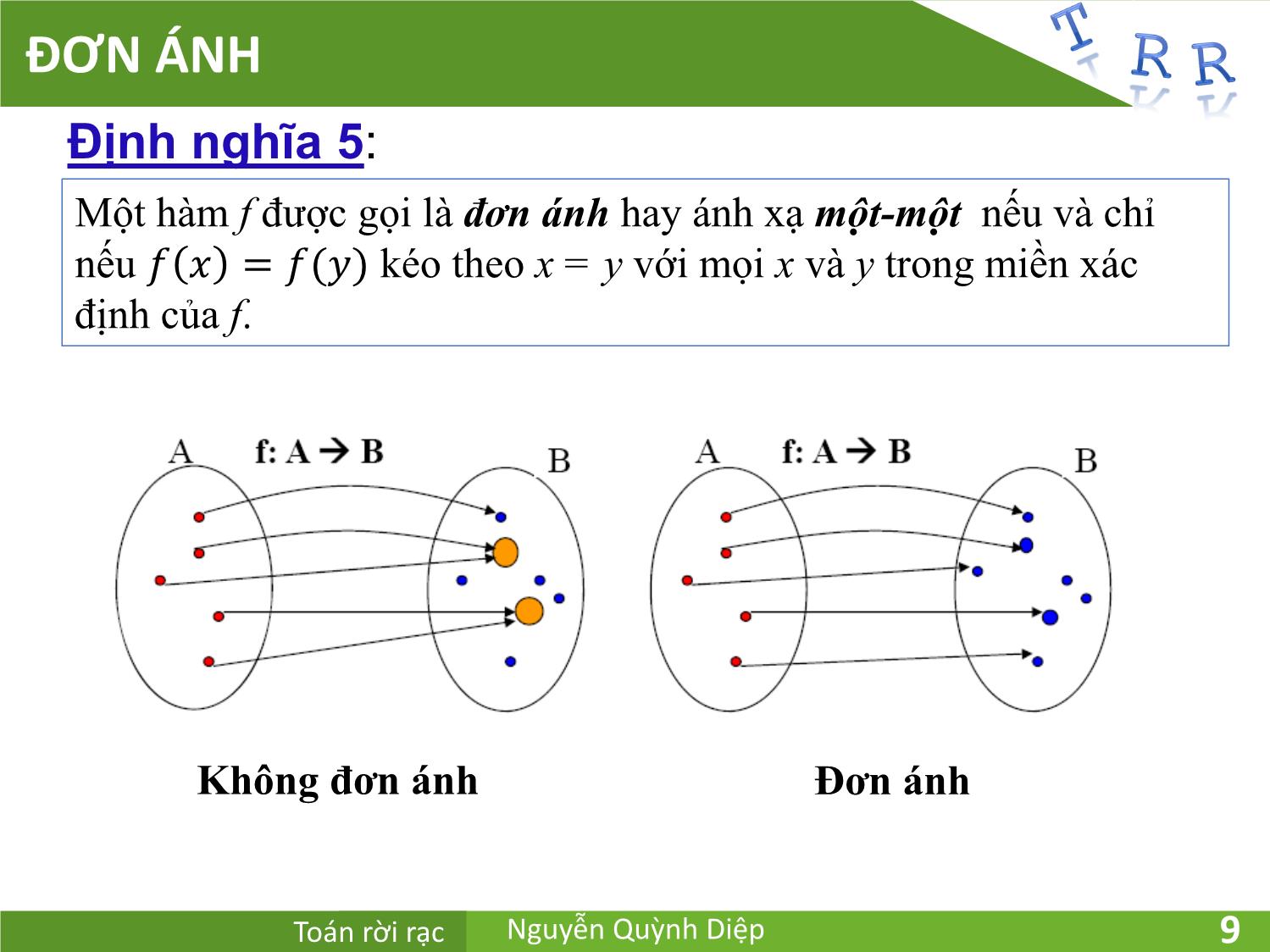
ĐƠN ÁNH
 Định nghĩa 5:
 Một hàm f được gọi là đơn ánh hay ánh xạ một-một nếu và chỉ 
 nếu = ( ) kéo theo x = y với mọi x và y trong miền xác 
 định của f.
 Không đơn ánh Đơn ánh
 Toán rời rạc Nguyễn Quỳnh Diệp 9
ĐƠN ÁNH
 Các hàm sau có là hàm đơn ánh không?
Ví dụ 1:
 • Cho A = {1, 2, 3} và B = {a, b, c}, hàm f được cho như sau:
 • 1 → , 2 → , 3 → 
Ví dụ 2:
 • Cho g: 푍 → 푍 , với g(x) = 2x - 1
Ví dụ 3:
 • Hàm f(x) = x2 , x thuộc tập các số nguyên, miền giá trị của f
 cũng là tập các số nguyên.
 Toán rời rạc Nguyễn Quỳnh Diệp 10
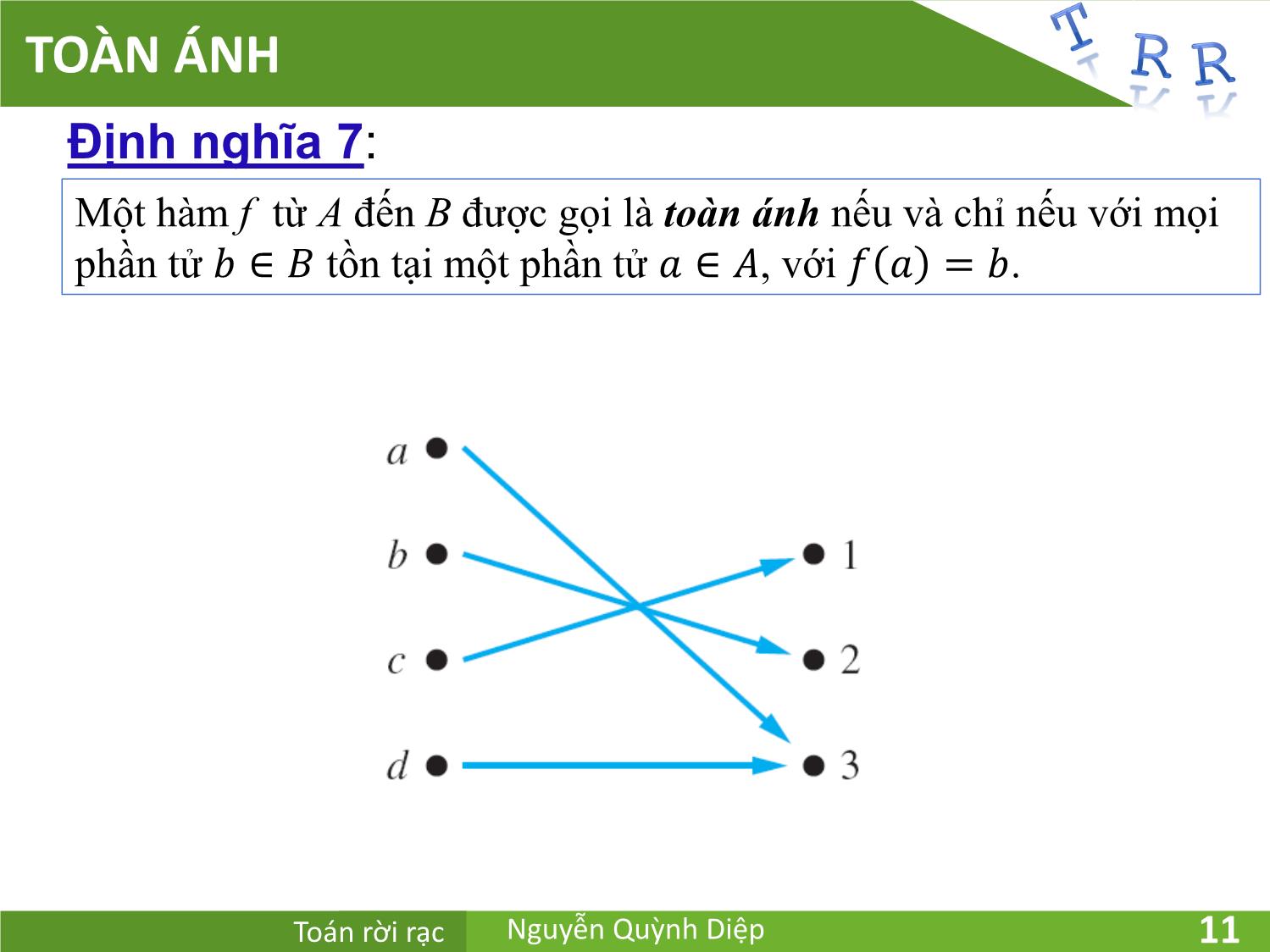
TOÀN ÁNH
 Định nghĩa 7:
 Một hàm f từ A đến B được gọi là toàn ánh nếu và chỉ nếu với mọi 
 phần tử ∈ tồn tại một phần tử ∈ , với = .
 Toán rời rạc Nguyễn Quỳnh Diệp 11
TOÀN ÁNH
 Các hàm sau có là hàm toàn ánh không?
Ví dụ 1:
 • Hàm f: Z → Z, với f(x) = x + 1.
Ví dụ 2:
 • Hàm f(x) = x2 , x thuộc tập các số nguyên, miền giá trị của f
 cũng là tập các số nguyên.
 Toán rời rạc Nguyễn Quỳnh Diệp 12
SONG ÁNH
Định nghĩa 8:
Một hàm f là một song ánh nếu nó vừa là đơn ánh vừa là toàn ánh.
 (1)? (2)? (3)? (4)? (5)?
 Toán rời rạc Nguyễn Quỳnh Diệp 13
ĐỒ THỊ CỦA HÀM
 Định nghĩa 11:
 Cho f là hàm từ tập A đến tập B. Đồ thị của hàm f là tập các cặp sắp 
 thứ tự , | ∈ 풗à 풇 = .
 = 2 + 1 = 2
 Một số hàm quan trọng:
 • Hàm sàn
 • Hàm trần
 Toán rời rạc Nguyễn Quỳnh Diệp 14
HÀM SÀN, HÀM TRẦN
 Định nghĩa 12:
 Hàm sàn gán cho số thực x số nguyên lớn nhất có giá trị nhỏ hơn 
 hoặc bằng x. Giá trị của hàm sàn được kí hiệu x . Hàm trần gán 
 cho số thực x số nguyên nhỏ nhất có giá trị lớn hơn hoặc bằng x. Giá 
 trị của hàm trần được kí hiệu là x .
Ví dụ:
 • 2,1 = ?
 • 2,1 = ?
 • -2,1 = ?
 • -2,1 = ?
 Toán rời rạc Nguyễn Quỳnh Diệp 15
BÀI TẬP
. Bài 1: Hãy xác định xem hàm f: 푍 → 푍 có là đơn ánh không?
 a) 푛 = 푛 − 1 b) 푛 = 푛2+1
. Bài 2: Hãy xác định xem hàm f: 푍 × 푍 → 푍 có toàn ánh không?
 a) , 푛 = 2 − 푛 b) , 푛 = + |푛|
. Bài 3: Hãy xác định xem hàm f: 푅 → 푅 có song ánh không?
 ( +1)
 a) = −3 + 4 b) =
 ( +2)
 16
 Toán rời rạc Nguyễn Quỳnh Diệp
 2.2. ĐỘ TĂNG CỦA HÀM
Toán rời rạc Nguyễn Quỳnh Diệp 17
BIG-O
 Đánh giá thuật toán như thế nào?
 • Thời gian đòi hỏi để giải một bài toán phụ thuộc vào số phép 
 toán được sử dụng
 • Ước lượng thời gian bằng cách nhân thời gian đòi hỏi với 
 một hằng số.
 • Sử dụng khái niệm big-O: đánh giá số phép toán được dùng 
 trong một thuật toán khi đầu vào của nó tăng
Định nghĩa 1:
 Cho hàm f và g là hai hàm từ tập các số nguyên hoặc số thực đến
 tập các số thực. Ta nói f(x) là O(g(x)) (đọc là f(x) là big-O của g(x) 
 nếu tồn tại hai hằng số C và k sao cho:
 풇 풙 ≤ 푪 품 풙 , với mọi x>k
 Toán rời rạc Nguyễn Quỳnh Diệp 18
BIG-O
Ví dụ : Chứng minh rằng f(x) = x2 +2x+1 là O(x2)
 Toán rời rạc Nguyễn Quỳnh Diệp 19
MỘT SỐ KẾT QUẢ QUAN TRỌNG
 Định lí 1:
 n n-1
 Cho f(x) = anx + an-1x + ... + a1x + a0 , ở đây a0, a1, ..., an là 
 các số thực. Khi đó f(x) là O(xn).
 • 1+ 2 + ... + n là O(n2)
 • n! là O(nn)
 • logn! là O(nlogn)
 • logn là O(n)
 Toán rời rạc Nguyễn Quỳnh Diệp 20
MỘT SỐ KẾT QUẢ QUAN TRỌNG
 Định lí 2:
 Cho f1(x) là O(g1(x)) và f2(x) là O(g2(x)). Khi đó (f1 + f2)(x) là 
 O(max(|g1(x)| , |g2(x)|)).
 Hệ quả 1:
 Cho f1(x) và f2(x) đều là O(g(x)). Khi đó (f1 + f2)(x) là O(g(x)).
 Định lí 3:
 Cho f1(x) là O(g1(x)) và f2(x) là O(g2(x)). Khi đó (f1 f2)(x) là 
 O(g1(x) g2(x)).
 Toán rời rạc Nguyễn Quỳnh Diệp 21
MỘT SỐ KẾT QUẢ QUAN TRỌNG
 Ví dụ 1 : Cho một đánh giá big-O đối với hàm:
 f(n) = 3nlog(n!) + (n2 + 3) logn
 Ví dụ 2 : Cho một đánh giá big-O đối với hàm:
 f(x) = (x+1)log(x2 + 1) + 3x2
 Toán rời rạc Nguyễn Quỳnh Diệp 22
BÀI TẬP
. Bài 3: Với các hàm g(x) sau đây x3 có là O(g(x)) không:
 a) g(x) = x2
 b) g(x) = x3
 c) g(x) = x2 + x3
 23
 Toán rời rạc Nguyễn Quỳnh Diệp
BIG-OMEGA
 Định nghĩa 2:
 Cho f và g là hai hàm từ tập các số nguyên hoặc tập các số thực
 đến tập các số thực. Nói rằng f(x) là (g(x)) nếu và chỉ nếu tồn tại
 các hằng số C và k, sao cho:
 |f(x)| C|g(x)| với mọi x > k
 Ví dụ: Hàm f(x) = 8x3 + 5x2 + 7 là (g(x)), với g(x) = x3.
 Toán rời rạc Nguyễn Quỳnh Diệp 24
BIG-THETA
 Định nghĩa 3:
 Cho f và g là hai hàm từ tập các số nguyên hoặc tập các
 số thực đến tập các số thực. Nói rằng f(x) là (g(x)) nếu
 và chỉ nếu f(x) là O(g(x)) và f(x) là (g(x)). 
 Khi f(x) là (g(x)) ta nói f(x) cùng bậc với g(x).
 Ví dụ: Chứng minh rằng 3x2 + 8xlogx là (x2).
 Toán rời rạc Nguyễn Quỳnh Diệp 25
KẾT QUẢ QUAN TRỌNG
Định lí 4:
 n n-1
 Cho f (x) = anx + an-1x + ...+ a1x + a0, trong đó a0, a1, ..., an là 
 n
 các số thực với an 0. Khi đó f(x) cùng bậc với x .
 Toán rời rạc Nguyễn Quỳnh Diệp 26
BÀI TẬP
. Bài 4: Chứng minh rằng:
 a) 3x + 7 là (x) 
 b) 2x2 + x – 7 là (x2) 
 c) log10(x) là (log2 (x)) 
 27
 Toán rời rạc Nguyễn Quỳnh Diệp
 2.3. THUẬT TOÁN
Toán rời rạc Nguyễn Quỳnh Diệp 28
THUẬT TOÁN
 Định nghĩa 1:
 Thuật toán là tập hợp hữu hạn các lệnh chính xác để thực hiện tính 
 toán hoặc giải một bài toán.
 Tính chất của thuật toán
 • Đầu vào
 • Đầu ra
 • Tính xác định
 • Tính đúng đắn
 • Tính hữu hạn
 • Tính hiệu quả
 • Tính tổng quát
 Toán rời rạc Nguyễn Quỳnh Diệp 29
THUẬT TOÁN
 Mô tả thuật toán
 • Dùng ngôn ngữ tự nhiên
 • Dùng giả mã
 • Sử dụng lưu đồ
 • Sử dụng ngôn ngữ lập trình
 Ví dụ :
 THUẬT TOÁN : Tìm phần tử lớn nhất trong dãy hữu hạn
 Procedure max(a1, a2, ... an: số nguyên)
 max := a1
 for i := 2 to n
 if max < ai then max := ai
 { max là phần tử lớn nhất}
 Toán rời rạc Nguyễn Quỳnh Diệp 30
MỘT SỐ THUẬT TOÁN TÌM KIẾM
 • Tìm kiếm là bài toán xác định vị trí của một phần tử trong bảng 
 liệt kê
 • Tổng quát: xác định vị trí x trong dãy a1, a2, a3, ... an
 • 2 loại thuật toán tìm kiếm:
 • Tìm kiếm tuyến tính
 • Tìm kiếm nhị phân
 Toán rời rạc Nguyễn Quỳnh Diệp 31
MỘT SỐ THUẬT TOÁN TÌM KIẾM
 Tìm kiếm tuyến tính
 • So sánh x với a1, nếu x = a1 thì vị trí tìm được là 1
 • Khi x a1 so sánh x với a2
 • ......
 THUẬT TOÁN : Thuật toán tìm kiếm tuyến tính
 Procedure linear search (x: nguyên, a1, a2, ... an: các số nguyên phân biệt)
 i := 1
 while (푖 ≤ 푛 푣à ≠ 푖)
 i := i + 1 
 if 푖 ≤ 푛 then location := i
 else location := 0
 { location là chỉ số của số hạng bằng x hoặc là 0 nếu không tìm được x}
 Toán rời rạc Nguyễn Quỳnh Diệp 32
MỘT SỐ THUẬT TOÁN TÌM KIẾM
 Tìm kiếm nhị phân
 • Sử dụng cho dãy đã sắp xếp tăng dần
 • So sánh phần tử x với số hạng ở giữa của dãy, nếu bằng 
 thì trả về vị trí cần tìm
 • Nếu x nhỏ hơn tìm bên trái dãy
 • Nếu x lớn hơn tìm bên phải dãy
Ví dụ : • Tìm kiếm giá trị 15 trong dãy:
 1 3 5 6 8 9 10 15 24 39
 Toán rời rạc Nguyễn Quỳnh Diệp 33
MỘT SỐ THUẬT TOÁN TÌM KIẾM
 THUẬT TOÁN : Thuật toán tìm kiếm nhị phân
 Procedure binary search (x: nguyên, a1, a2, ... an: các số nguyên tăng dần)
 i := 1 {i là điểm mút trái của khoảng tìm kiếm}
 j := n {j là điểm mút phải của khoảng tìm kiếm}
 while 푖 < 푗
 begin
 m := (푖 + 푗)/2 
 if > then i:= m + 1
 else j:= m
 end
 if x = a then location :=i
 else location :=0
 { location là chỉ số của số hạng bằng x hoặc là 0 nếu không tìm được x}
 Toán rời rạc Nguyễn Quỳnh Diệp 34
MỘT SÔ THUẬT TOÁN SẮP XẾP
 Sắp xếp kiểu nổi bọt
 • So sánh liên tiếp các phần tử kề nhau
 • Đổi chỗ cho nhau nếu chúng chưa có thứ tự đúng
Ví dụ : • Sắp xếp danh sách 3, 2, 4, 1, 5.
 Vòng lặp 1 Vòng lặp 2
 Vòng lặp 4
 Vòng lặp 3 Đổi chỗ
 Cặp đã đúng thứ tự
 Toán rời rạc Nguyễn Quỳnh Diệp 36
MỘT SỐ THUẬT TOÁN SẮP XẾP
 THUẬT TOÁN : Thuật toán sắp xếp nổi bọt
 Procedure bubble sort (a1, a2, ... an)
 for i:= 1 to n -1 
 for j:=1 to n-i
 if aj > aj+1 then đổi chỗ aj và aj+1
 {a1, a2, ..., an đã được sắp xếp}
 Toán rời rạc Nguyễn Quỳnh Diệp 37
MỘT SỐ THUẬT TOÁN SẮP XẾP
 Sắp xếp kiểu chèn
 • Bắt đầu với phần tử thứ 2
 • So sánh phần tử thứ 2 với phần tử thứ nhất:
 • Chèn vào trước phần tử thứ nhất nếu nhỏ hơn hoặc bằng
 • Chèn vào sau phần tử thứ nhất nếu lớn hơn
 • So sánh phần tử thứ 3 với phần tử thứ nhất và so sánh tiếp với 
 phần tử thứ 2.
Ví dụ :
 • Sắp xếp danh sách 4, 3, 2, 1, 2, 5.
 Toán rời rạc Nguyễn Quỳnh Diệp 38
MỘT SỐ THUẬT TOÁN SẮP XẾP
 THUẬT TOÁN : Thuật toán sắp xếp kiểu chèn
 Procedure insertion sort (a1, a2, ... an: các số thực với 푛 ≥ 2)
 for j:= 2 to n
 begin
 i:=1
 while ai < aj
 i := i + 1
 m := aj
 for k:= j downto i+1
 ak := ak-1
 ai := m
 end {a1, a2, ..., an đã được sắp xếp}
 Toán rời rạc Nguyễn Quỳnh Diệp 39
BÀI TẬP
. Bài 2: Sắp xếp danh sách 6, 2, 3, 1, 5, 4 theo thứ tự tăng dần bằng 
 phương pháp:
 a) Sắp xếp kiểu nổi bọt
 b) Sắp xếp kiểu chèn
 c) Sắp xếp kiểu lựa chọn (tham khảo trong sách)
 d) Sắp xếp kiểu chèn nhị phân (tham khảo trong sách)
 40
 Toán rời rạc Nguyễn Quỳnh Diệp
2.4. ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
 Toán rời rạc Nguyễn Quỳnh Diệp 41
ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
 Hiệu quả của một thuật toán:
 • Thời gian mà máy tính sử dụng để giải bài toán
 • Dung lượng bộ nhớ đòi hỏi khi thực hiện thuật toán
 Độ phức tạp thời gian:
 • Biểu diễn qua số các phép toán được dùng trong thuật toán
 • Các phép toán để đo:
 • Phép so sánh
 • Phép cộng, trừ, nhân, chia
 Ví dụ: Độ phức tạp thời gian của thuật toán tìm kiếm phần tử lớn 
 nhất là (n)
 Toán rời rạc Nguyễn Quỳnh Diệp 42
 ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
 Độ phức tạp trong trường hợp xấu nhất:
 • Là trường hợp phải dùng tối đa các phép toán để giải bài 
 toán theo thuật toán đang xét.
Ví dụ 1: Xác định độ phức tạp trong trường hợp xấu nhất của thuật 
 toán sắp xếp kiểu nổi bọt qua số các phép so sánh
Ví dụ 2: Xác định độ phức tạp trong trường hợp xấu nhất của thuật 
 toán sắp xếp kiểu chèn qua số các phép so sánh
 Toán rời rạc Nguyễn Quỳnh Diệp 43
 ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
 Độ phức tạp trong trường hợp trung bình:
 • Tìm số bước trung bình các phép toán được dùng để giải 
 toàn bộ các giá trị đầu vào
 • Phức tạp hơn phân tích trong trường hợp xấu nhất
Ví dụ 1: Mô tả sự phân tích trong trường hợp trung bình của thuật
 toán tìm kiếm tuyến tính với giả thiết rằng phần tử x có
 mặt trong bảng liệt kê và dựa vào phép so sánh.
 Toán rời rạc Nguyễn Quỳnh Diệp 44
ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
 Các thuật ngữ thường dùng cho độ phức tạp tính toán
 Độ phức tạp Thuật ngữ
 O(1) Độ phức tạp hằng số
 O(logn) Độ phức tạp logarit
 O(n) Độ phức tạp tuyến tính
 O(nlogn) Độ phức tạp nlogn
 O(nb) Độ phức tạp đa thức
 O(bn) Độ phức tạp hàm mũ
 O(n!) Độ phức tạp giai thừa
 Toán rời rạc Nguyễn Quỳnh Diệp 45
ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
Kích Các phép toán bit được sử dụng
thước bài 
toán
n logn n nlogn n2 2n n!
10 3.10-9s 10-8s 3.10-8s 10-7s 10-6s 3.10-3s
100 7.10-9s 10-7s 7.10-7s 10-5s 4.1013 *
 năm
1000 10-8s 10-6s 10-5s 10-3s * *
10000 1.3*10-9s 10-5s 10-4s 10-1s * *
105 1.7*10-8s 10-4s 2*10-3s 10s * *
106 2*10-8s 10-3s 2*10-2s 17 phút * *
 Toán rời rạc Nguyễn Quỳnh Diệp 46
 47
Nguyễn Quỳnh Diệp