Bài giảng Toán rời rạc 1 - Chương IV: Đại số Bool - Võ Văn Phúc
(Bản scan)
| Hàm Bool n biến là ánh xạ
| f: Bn » B, trong đó B = {0, 1}. Như vậy hàm Bool n biến là một hàm số có dạng: f = f(x1,x2,...,x), trong đó mỗi biến trong x,, X2,..., X, chỉ nhận hai giá trị 0, 1 và f nhận giá trị trong B = {0, 1}.
Ký hiệu FB để chỉ tập các hàm Boonbiến. Ví dụ. Dạng mệnh đề E = Eếp, p,...,P.) theo n biến p, pa,..., P. là một hàm Bool n biến.

Trang 1

Trang 2
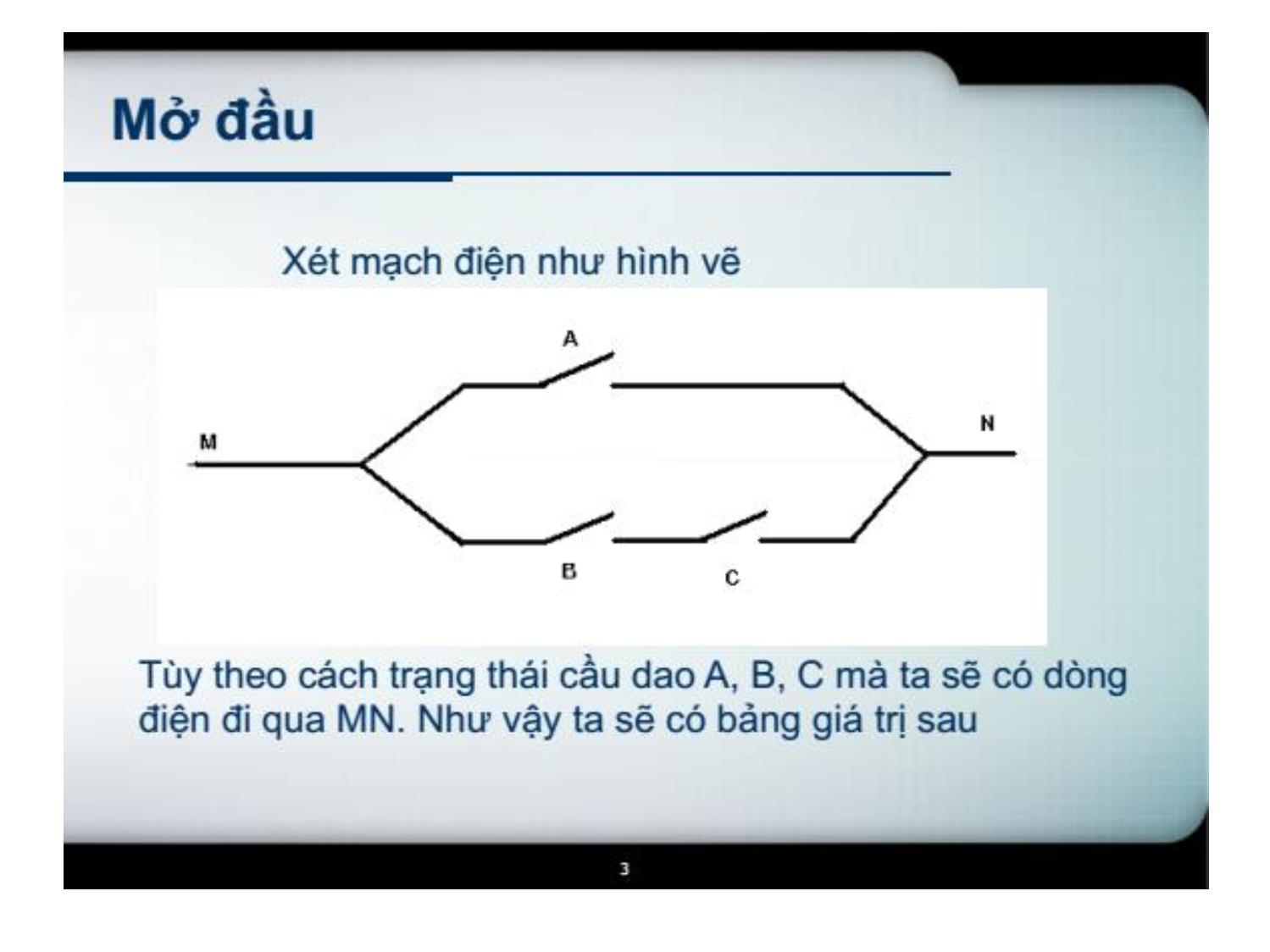
Trang 3
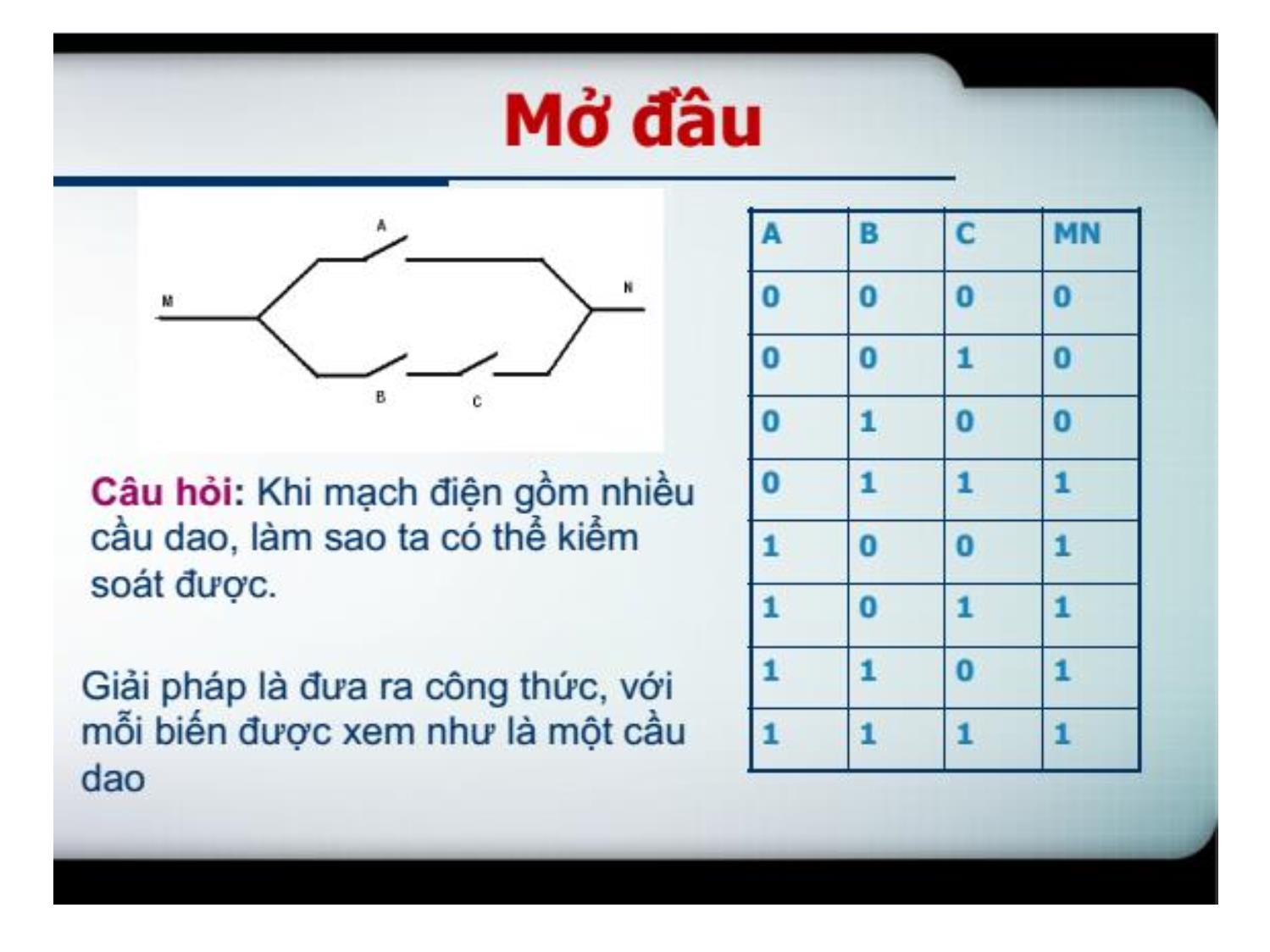
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
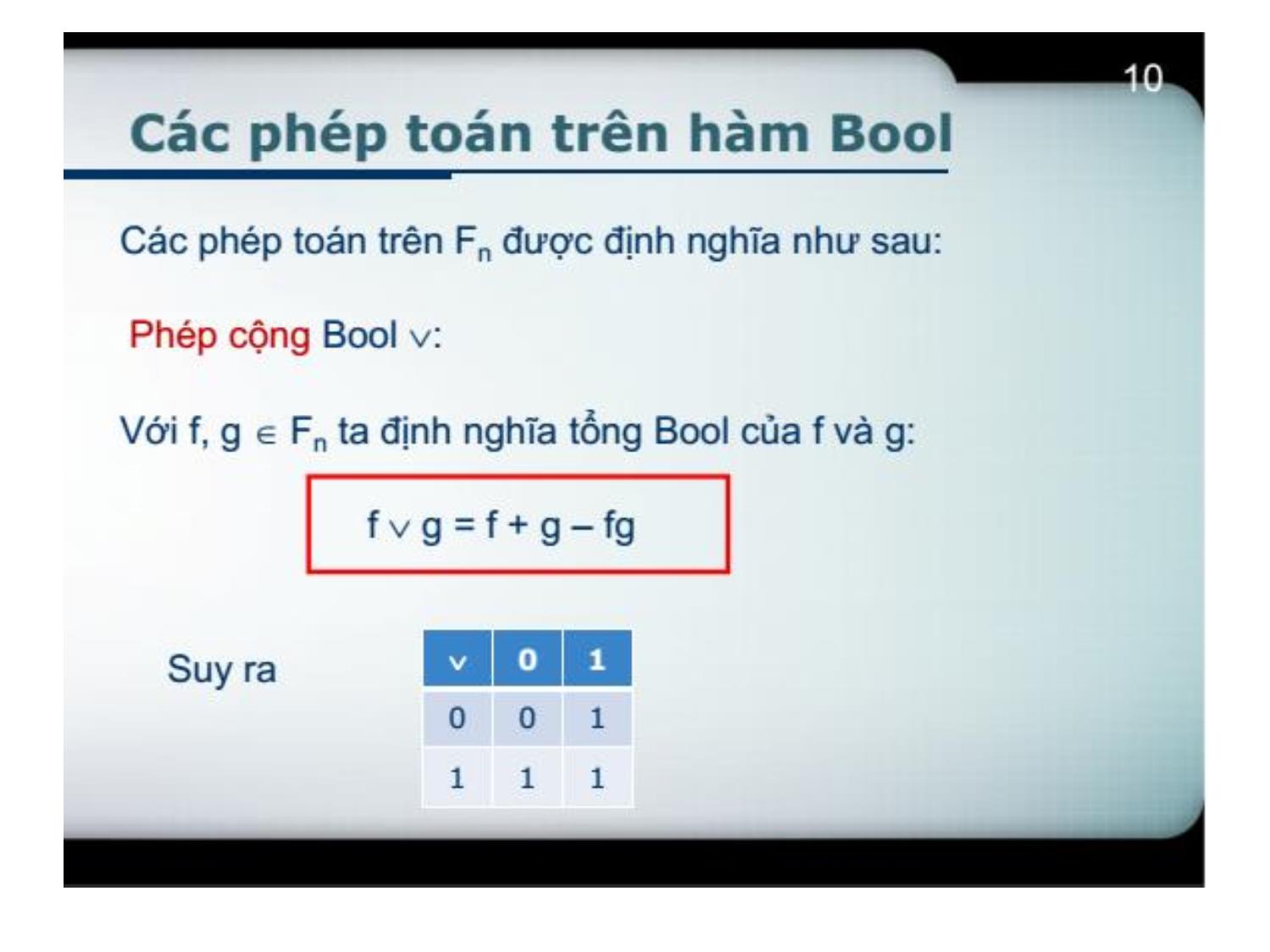
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc 1 - Chương IV: Đại số Bool - Võ Văn Phúc", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
File đính kèm:
 bai_giang_toan_roi_rac_1_chuong_iv_dai_so_bool_vo_van_phuc.pdf
bai_giang_toan_roi_rac_1_chuong_iv_dai_so_bool_vo_van_phuc.pdf

