Bài giảng Toán rời rạc 1 - Chương II.1: Tập hợp - Võ Văn Phúc

1.1 Giới thiệu về tập hợp: 
- Tập hợp là một khái niệm không định nghĩa mà chỉ có thể mô tả, một 
tập hợp được xác định khi đưa ra một qui tắc. Các tập hợp thường 
được dùng để nhóm các đối tượng lại với nhau. 
- Các đối tượng trong tập hợp có các tính chất tương tự nhau. 
- Mỗi đối tượng thuộc tập hợp còn gọi là “phần tử” của tập hợp. 
Ký hiệu: A, B, P, Q, R ký hiệu cho các tập hợp, các chữ in thường x, y, 
z ký hiệu cho các phần tử của tập hợp. 
Mục tiêu nghiên cứu của lý thuyết tập hợp là tìm ra những qui luật biến 
đổi, phương pháp tương tác giữa các đối tượng trong một tập hợp và 
trong các tập hợp khác nhau. 
 Tập hợp được biểu diễn bằng biểu đồ Ven (biểu đồ Ven là 
 đường cong khép kín, bên trong chứa các phần tử thuộc 
 tập hợp đó). 
 Biểu đồ 
 Ven của 
 tập A 
 Ta xét các tập hợp 
 A 0,1,2,3,4,5,6 M x R,x 3 0
 Tập A được cho bằng phương pháp liệt kê (số 
 phần tử là hữu hạn), tập M được cho bằng 
 phương pháp mô tả. 
 Tập các số thực R, tập các số tự nhiên N, tập các 
 số phức C,  là các tập hợp có số phần tử vô hạn. 
1. Nhận biết các phần tử của tập hợp 
- x gọi là phần tử thuộc A thì ta viết x A hoặc A x và đọc “ A 
 chứa x” 
- x là phần tử không thuộc A thì ta viết x  A (hoặc xA ) 
- hoặc A x và đọc A không chứa x 
2. Tập con 
 Tập A được gọi là tập con của tập hợp X, nếu mọi phần tử của A 
 đều là phần tử của X. ký hiệu là AX 
(AX  x A x X) 
Đọc “ X bao hàm A” hoặc A là tập con của X 
 số phần tử trong một tập, còn gọi là bản số hay bậc của tập đó 
3. Tập hợp bằng nhau 
 Tập A được gọi là bằng tập B, nếu mọi phần tử của A là phần tử 
 của B và ngược lại mọi phần tử của B đều là phần tử của A 
A=B x A x B 
*) Chú ý: số phần tử trong một tập hợp còn gọi là bản số hoặc bậc 
4. Lực lượng 
Lực lượng của tập A là số phần tử trong A. Kí hiệu |A| hoặc N(A) 
Ví dụ: T={a, b, c} 
suy ra N(T)=3 
5. Tập các tập con 
 Cho A là một tập hợp, tập các tập con của A bao 
 gồm cả tập rỗng và A, ký hiệu p(A), trong tập này 
 mỗi phần tử là một tập con của A. 
Ví dụ: A={2,4,6} 
P(A)={{2},{4},{6},{2,4},{4.6},{2,4,6},{}} 
1. Liệt kê ra tất cả các phần tử của tập 
Nếu mọi phần tử x1, x2, .., xn đều thuộc A thì ta viết 
A={x1, x2,...,xn} 
2. Chỉ rõ tính chất đặc trưng của mọi phần tử thuộc tập 
Nếu tập A chứa các phần tử x có tính chất P thì ta viết 
A={x/P} 
3. Các tập vũ trụ thường dùng 
R={tập số thực} 
Z={tập số nguyên} 
Z + ={tập các số nguyên không âm} 
N={ tập các số tự nhiên} 
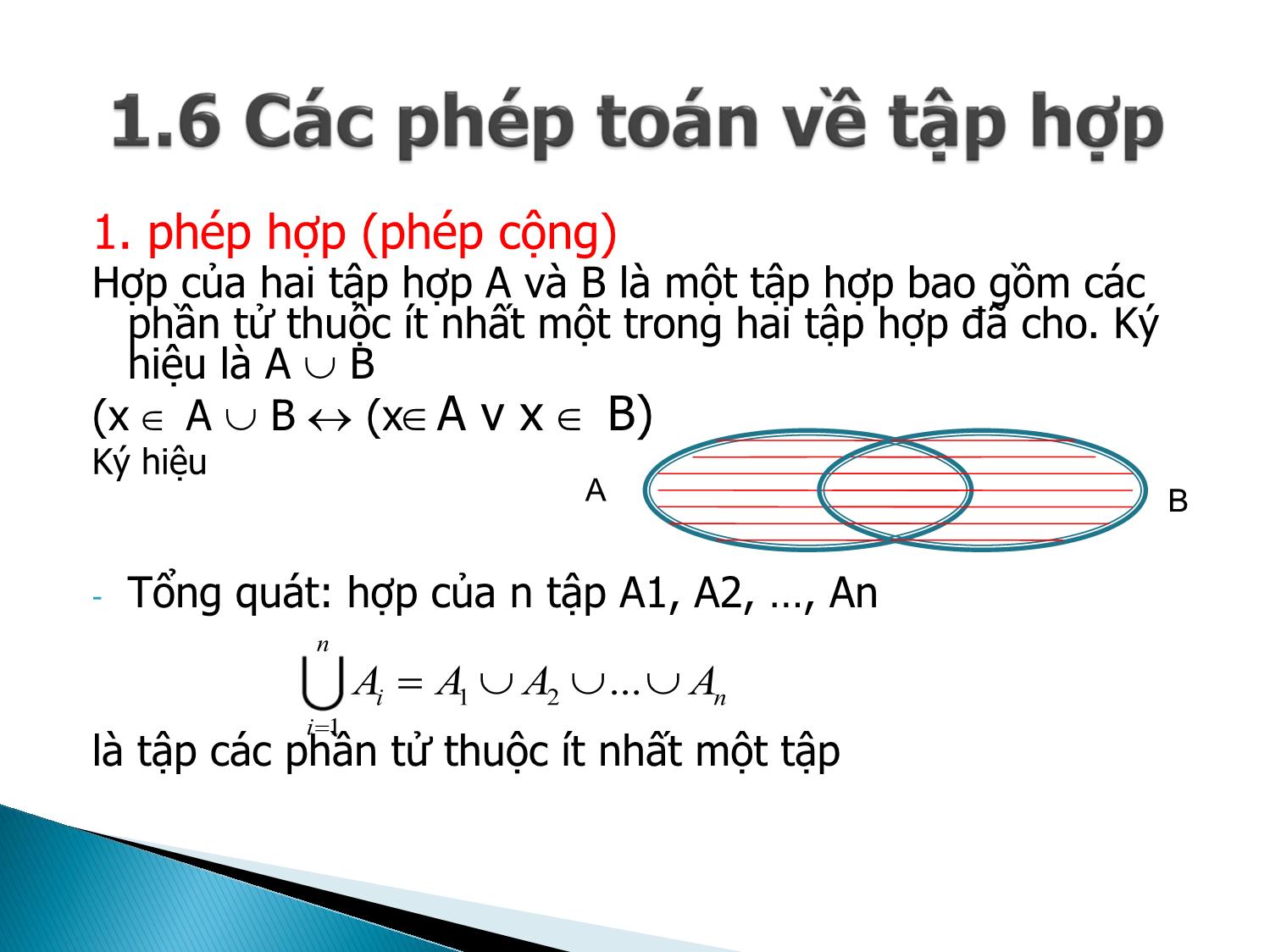
1. phép hợp (phép cộng) 
Hợp của hai tập hợp A và B là một tập hợp bao gồm các 
 phần tử thuộc ít nhất một trong hai tập hợp đã cho. Ký 
 hiệu là A  B 
(x A  B  (x A ν x B) 
Ký hiệu 
 A B 
- Tổng quát: hợp của n tập A1, A2, , An 
 n
 AAAA  ... 
 in12
 i 1
là tập các phần tử thuộc ít nhất một tập 
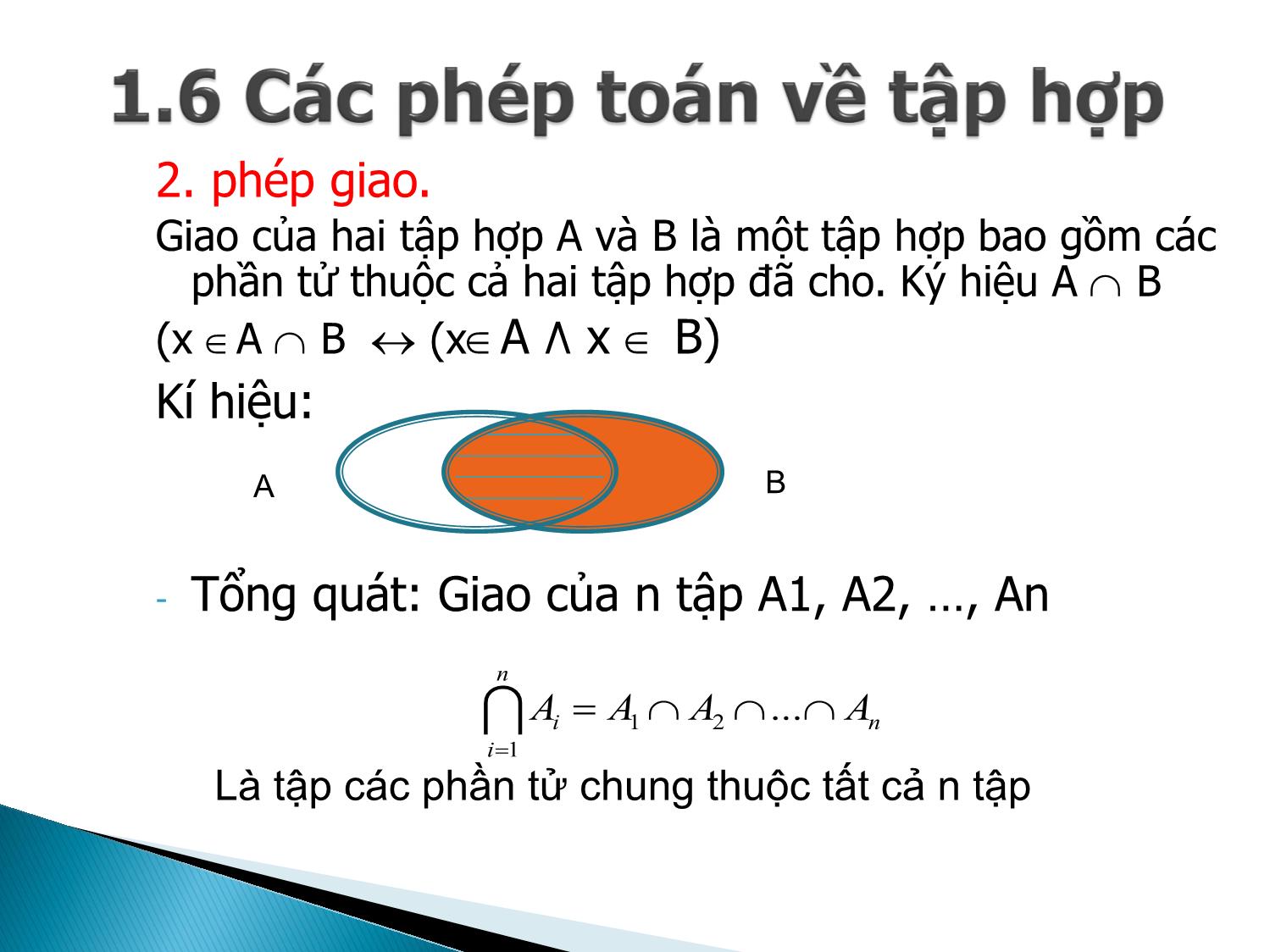
2. phép giao. 
Giao của hai tập hợp A và B là một tập hợp bao gồm các 
 phần tử thuộc cả hai tập hợp đã cho. Ký hiệu A  B 
 (x B ٨ x A  B  (x A)
Kí hiệu: 
 A B 
- Tổng quát: Giao của n tập A1, A2, , An 
 n
  Ai A1  A2 ... An
 i 1
 Là tập các phần tử chung thuộc tất cả n tập 
3. Phép hiệu: 
Cho A và B là 2 tập hợp hiệu của A và B, kí hiệu: 
 A\B là các phần tử thuộc A mà không thuộc B 
A\B={x|x A  x B} 
Kí hiệu: 
 A B 
- Tượng tự viết trường hợp B\A 
4. Hiệu đối xứng: 
Hiệu đối xứng của 2 tập A và B là 1 tập hợp . kÍ 
 hiệu A B 
A B={x|x A\B V x B\A} 
 A B 
5. Phần bù. 
Cho A là tập con thực sự của X, phần bù của tập A 
 trong X, ký hiệu Ā =X\A. gồm các phần tử thuộc X 
 mà không thuộc A 
Ā={x X và x A} 
Kí hiệu 
 x 
 X 
 A 
6. Tích đề các. 
Tích đề các của hai tập hợp A và B là một tập hợp bao gồm 
 các phần tử có dạng (a, b) trong đó a thuộc A, b thuộc B. 
ký hiệu A x B ={(a,b) | a A  b B} 
7. Tập rỗng 
Tập không có phần tử nào gọi là tập rỗng. Kí hiệu 
- Tập rỗng có hai tính chất: 
 + Tập rỗng là tập duy nhất 
 + Tập rỗng được xem là tập con của bất kỳ tập nào, kể 
 cả nó. 
Ví dụ: A={tập các nghiệm thực của phương trình x2 +1=0} 
A= 
a.A A
b.A 
c.A A 
d.A A X
1. Tính chất giao hoán 
 a. A  B= B  A 
 b. A  B = B  A 
2. Tính kết hợp 
 a. A  (B  C)=(A  B)  C 
 b. A  (B  C) = (A B)  C 
3. Tính chất phân phối 
 a. A (B  C) = (A  B)  (A  C) 
 b. A (B  C)= (A B) (A C) 
4. Luật đối ngẫu De Morgan 
 a. A\ (B  C)=(A\B) (A\C) 
 b. A\ (B C)=(A\B)(A\C) 
 c.A B A B
 d.A B A B
Ví dụ 1. Sử dụng các luật, chứng minh A B C C  B  A
 A  B  C = A  B C Theo luật De Morgan thứ nhất 
 = A B C Theo luật De Morgan thứ hai 
 = B C  A Theo luật giao hoán đối với phép giao 
 = C  B  A Theo luật giao hoán đối với phép hợp 
 Ví dụ 2. Dùng các tương đương logic để chứng minh A  B A  B
 A  B x | x A  B
 x | x A  x B 
 x | x A  x B
 x | x A  x B
 x | x A  B
 Bài 1: Liệt kê các phần tử của các tập sau: 
a. A={x R| (x-1)(2x2+3x+1)=0} 
b. B={x Z| (x2=x} 
c. C={x N| x là ước của 24} 
d. D={x N| x2+4x-5=0} 
 Bài 2: Viết lại các tập sau bằng cách chỉ ra tính 
 chất đặc trưng của các phần tử. 
a. A={5,10,15,20,25} 
b. B={-2,-1,0,1,2} 
c. C={1,1/2,1/4,1/8,...} 
Bài 3: Cho X={x N| x2 <=9}, X={x N| y2 <16}, 
Quan hệ nào sau đây là đúng? 
a. X  Y b. X  Y  c. X=Y d. Y\{4}=X 
Bài 4: cho A ={-2,1,0,3,4}. B={-1,2,3,5} 
1. Xác định các tập A B, A B, A \ B, B \ A, A B
2. Tìm các tập con của A và của B 
 Bài 5: cho A={-2,1,0,1,2}, B={0,1,2} 
Xác định các tập sau: 
a. {(x,y) AxB |x<y} 
b. {(x,y) AxB |y là ước của x} 
c. {(x,y) AxB |x2<=y2} 
d. {(x,y) AxB |x.y=0} 
Bài 6: Cho A={0,1,2,3,4,5}, B={0,3,5,6} 
Tìm A  B, A  B, A\B, A B 
Bài 7: chứng minh các luật De Morgan 
Bài 8: chứng minh các tính chất tập hơp 
1.8 BIỂU DIỄN TẬP HỢP TRÊN MÁY TÍNH 
Một tập hợp được biểu diễn trên máy tính có nhiều cách. 
 - Giả sử X là một tập vũ trụ, tập AX  , ta giả sử Xn (tập X có 
n phần tử), X {a 1 ,a 2 ,...,a n }. Ta sắp xếp (đánh số) các phần tử của X 
theo thứ tự. 
Khi đó ta có thể biểu diễn tập A trên máy tính bằng một xâu bit có 
chiều dài n, trong đó : 
 1, if a A
 A 
 0, if a A