Bài giảng Tin học ứng dụng nâng cao - Chương: Giải phương trình và hệ phương trình - Lê Viết Mẫn
Nội dung
1. Giải phương trình
2. Giải hệ phương trình
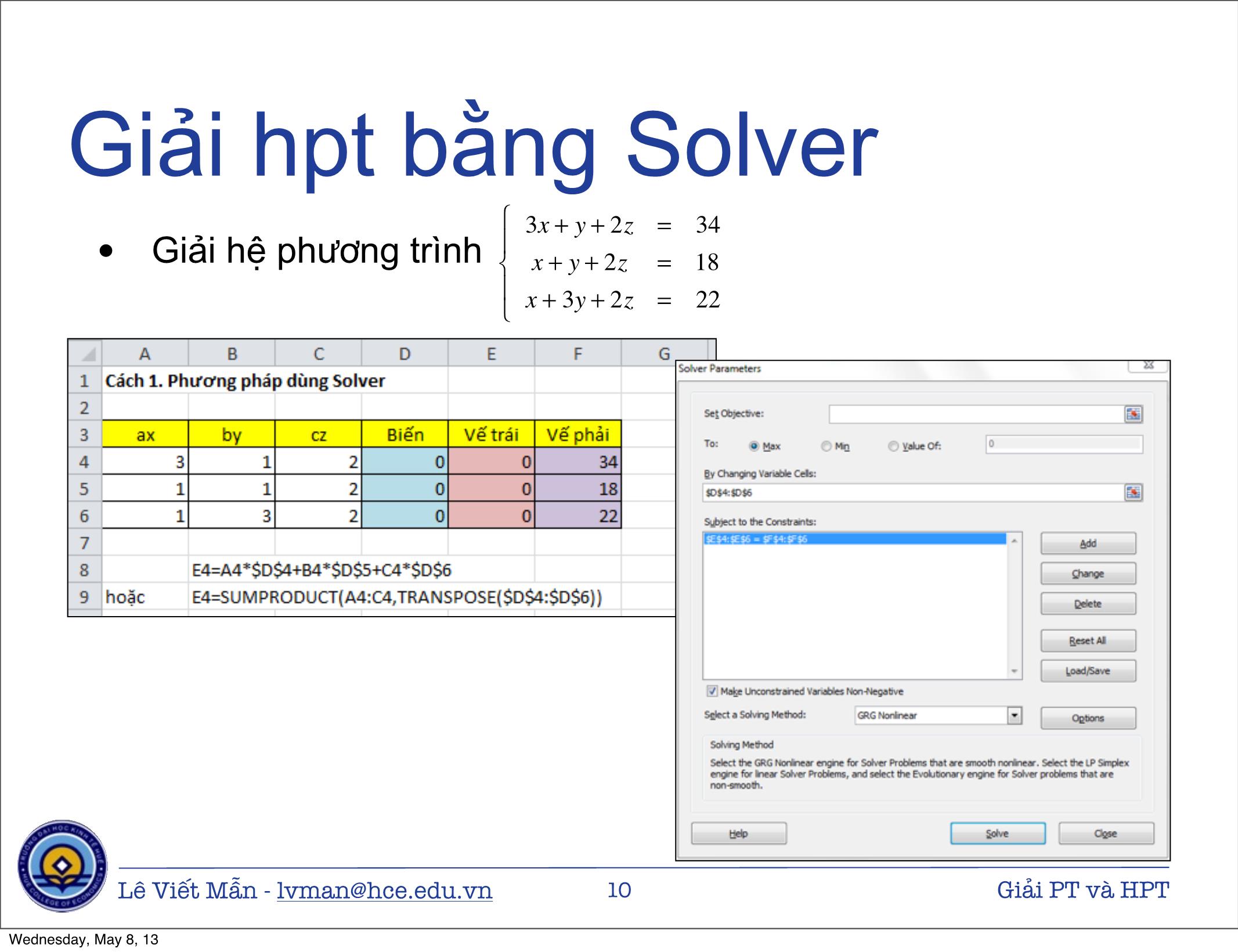
2.1. Bằng Solver
2.2. Bằng ma trận
Options (1/2)
Tham số Giải thích
Max Time Thời gian tối đa để giải bài toán, giá trị mặc định là 100
giây
Iterations Số lần lặp tối đa để giải bài toán, giá trị mặc định là 100
lần
Constraint Precision
Độ chính xác của bài toán. Tại đây có thể nhập vào các
số trong khoảng 0 và 1. Số càng gần 0 thì độ chính xác
càng cao. Giá trị này điều chỉnh sai số cho tập ràng buộc.
Giá trị mặc định là 1 phần triệu
Convergence
Độ hội tụ. Tại đây nhập vào các số trong khoảng 0 đến 1.
Giá trị càng gần 0 thì độ chính xác cao hơn và cần thời
gian nhiều hơn.
Use Automatic Scaling Chọn khi bài toán có sự khác biệt lớn giữa dữ liệu nhập
và xuất

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Tin học ứng dụng nâng cao - Chương: Giải phương trình và hệ phương trình - Lê Viết Mẫn

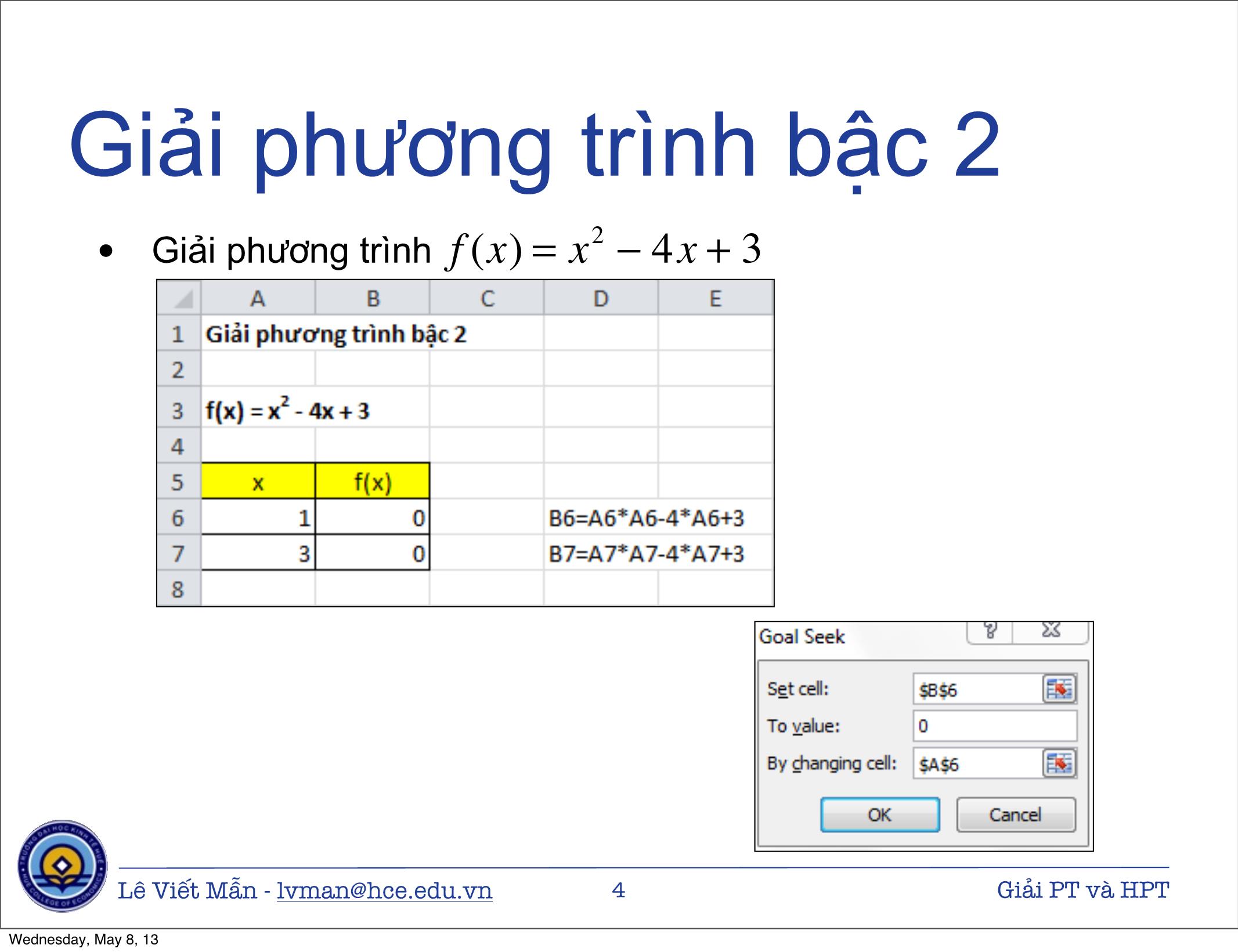
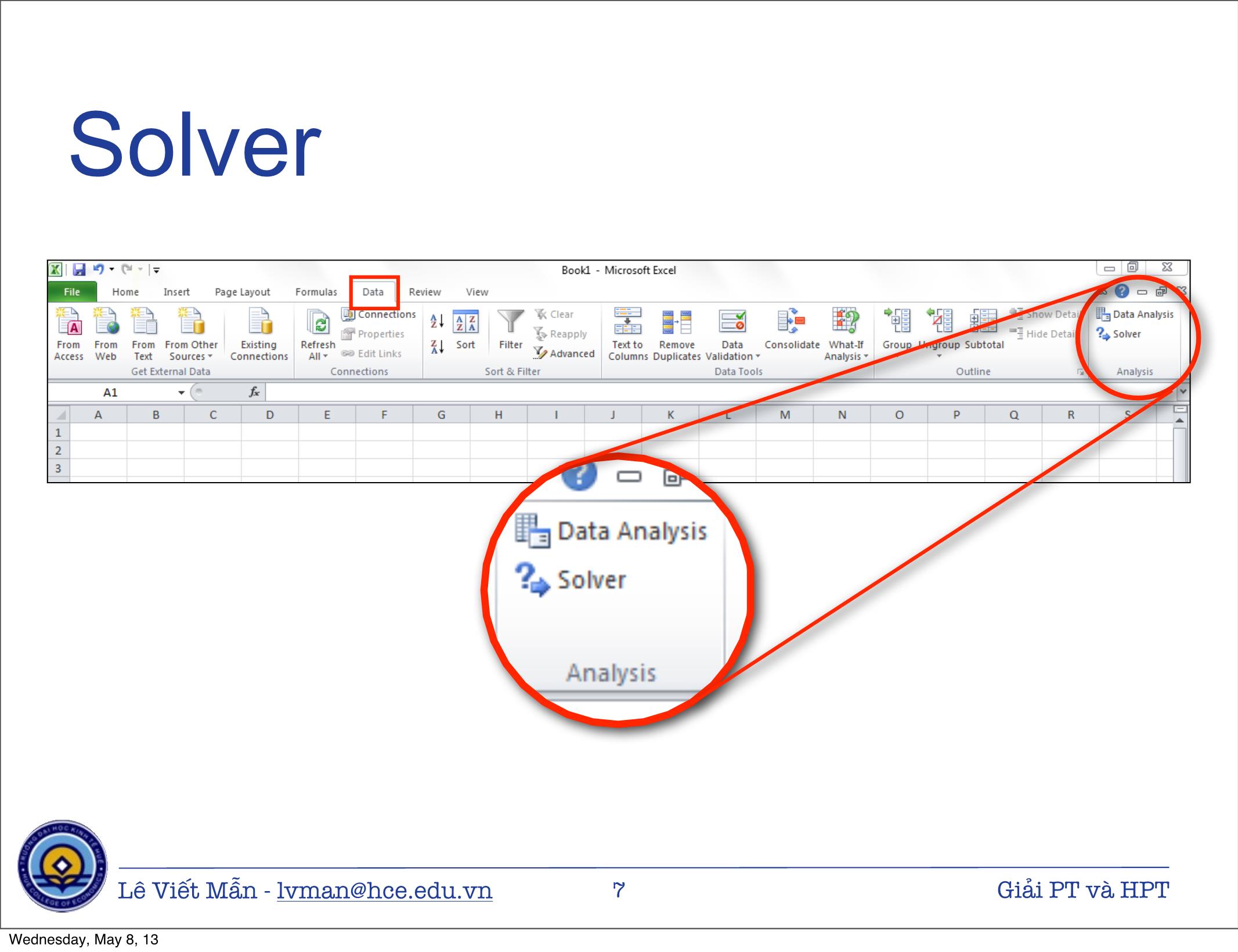
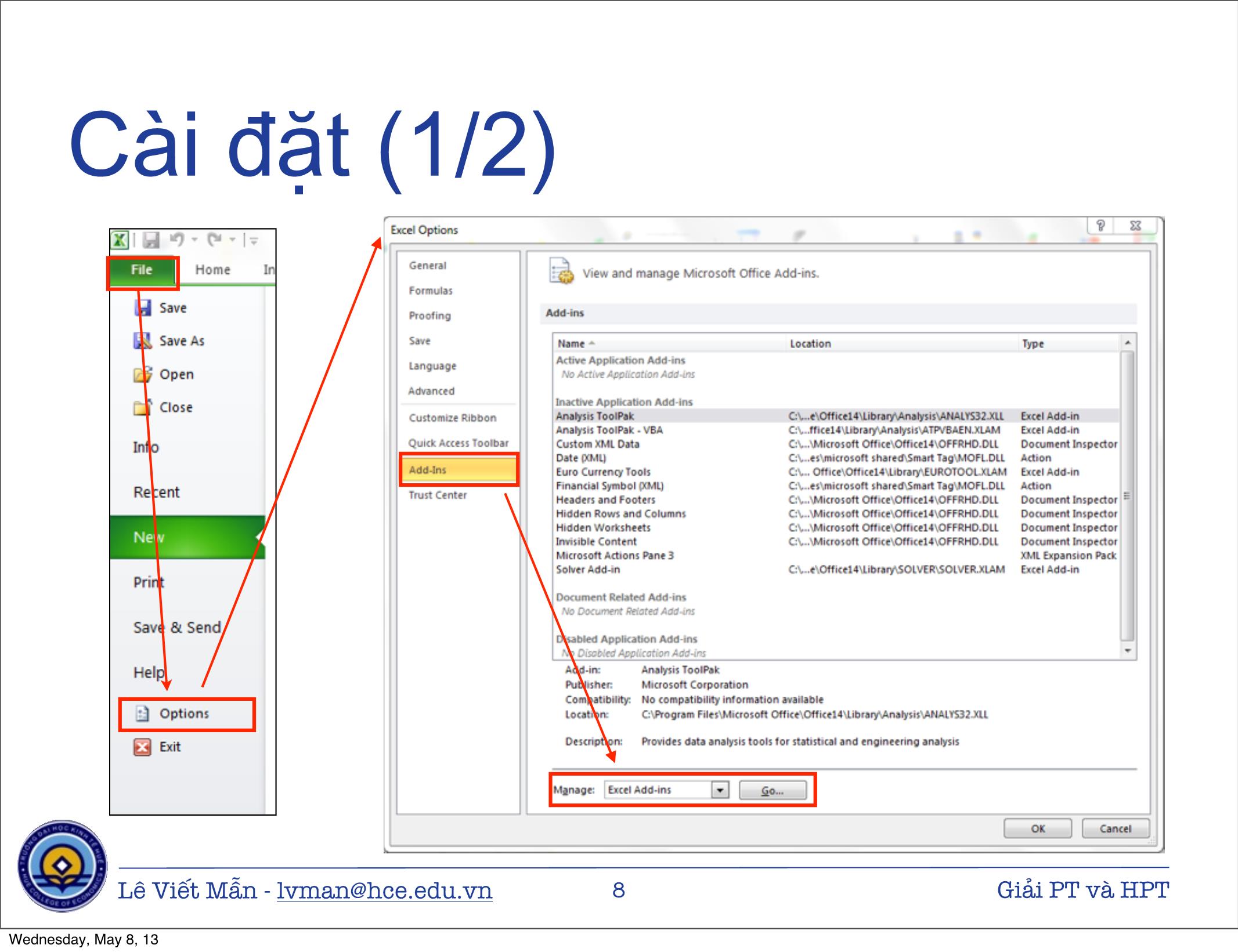
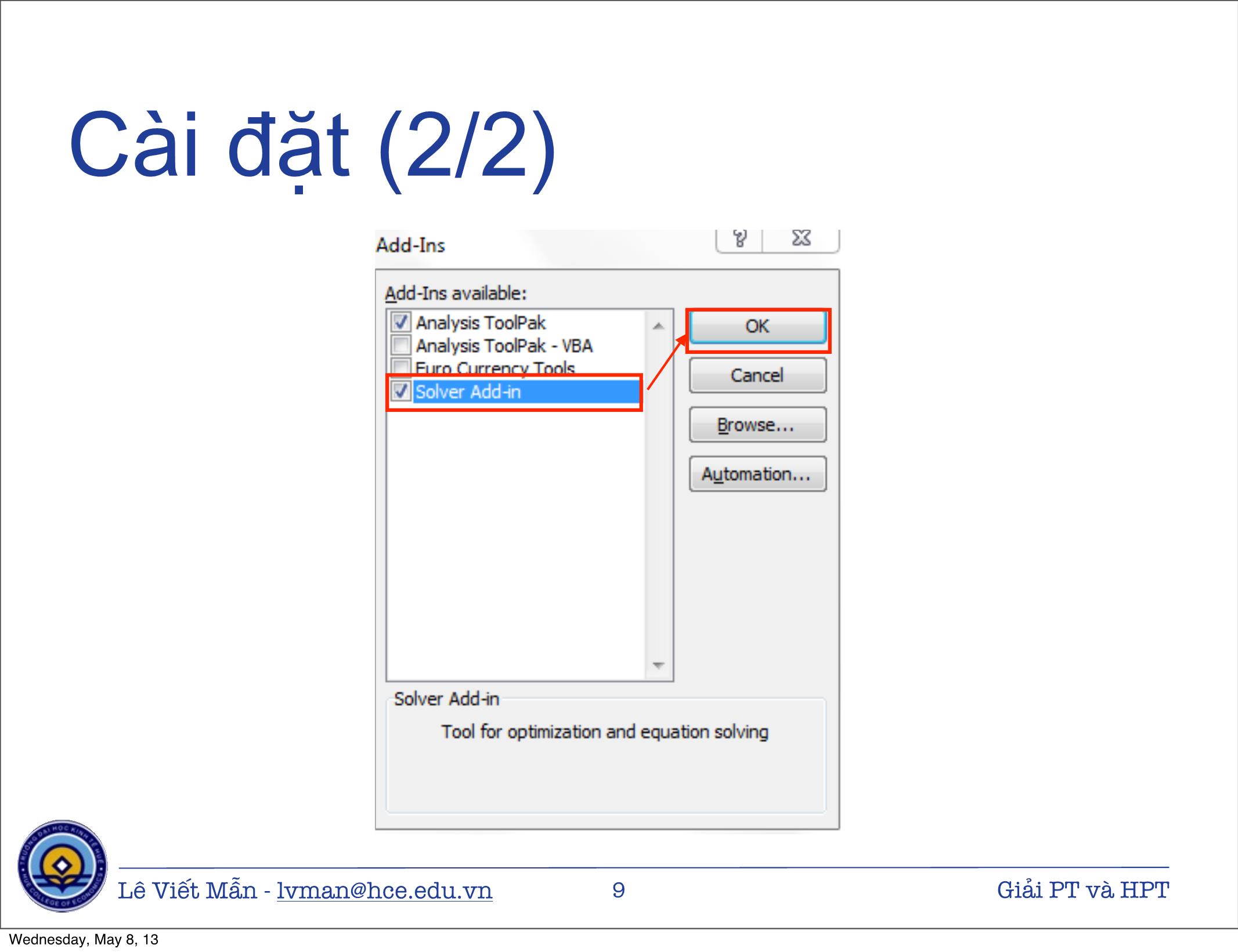
Giải phương trình và hệ phương trình v 1.1 - 04/2013 Lê Viết Mẫn - lvman@hce.edu.vn 1 Giải PT và HPT Wednesday, May 8, 13 Nội dung 1. Giải phương trình 2. Giải hệ phương trình 2.1. Bằng Solver 2.2. Bằng ma trận Lê Viết Mẫn - lvman@hce.edu.vn 2 Giải PT và HPT Wednesday, May 8, 13 Giải phương trình Lê Viết Mẫn - lvman@hce.edu.vn 3 Giải PT và HPT Wednesday, May 8, 13 Giải phương trình bậc 2 • Giải phương trình f (x) = x2 − 4x + 3 Lê Viết Mẫn - lvman@hce.edu.vn 4 Giải PT và HPT Wednesday, May 8, 13 Giải phương trình bậc 3 • Giải phương trình f (x) = x3 − 6x2 + 11x − 6 Lê Viết Mẫn - lvman@hce.edu.vn 5 Giải PT và HPT Wednesday, May 8, 13 Giải hệ phương trình Solver Lê Viết Mẫn - lvman@hce.edu.vn 6 Giải PT và HPT Wednesday, May 8, 13 Solver Lê Viết Mẫn - lvman@hce.edu.vn 7 Giải PT và HPT Wednesday, May 8, 13 Cài đặt (1/2) Lê Viết Mẫn - lvman@hce.edu.vn 8 Giải PT và HPT Wednesday, May 8, 13 Cài đặt (2/2) Lê Viết Mẫn - lvman@hce.edu.vn 9 Giải PT và HPT Wednesday, May 8, 13 Giải hpt bằng Solver ⎧ 3x + y + 2z = 34 ⎪ • Giải hệ phương trình ⎨ x + y + 2z = 18 ⎪ x + 3y + 2z = 22 ⎩ Lê Viết Mẫn - lvman@hce.edu.vn 10 Giải PT và HPT Wednesday, May 8, 13 Sử dụng Solver Set Objective - Địa chỉ To - Hàm mục tiêu của hàm mục tiêu muốn đạt đến Min, Max hay một giá trị By Changing Variable Cells - địa chỉ các biến của bài toán Subject to the Constraints - các ràng buộc của bài toán Thiết lập các thuộc tính cho Solver Lựa chọn phương pháp tính toán Bấm Solver để tính toán Lê Viết Mẫn - lvman@hce.edu.vn 11 Giải PT và HPT Wednesday, May 8, 13 Options (1/2) Tham số Giải thích Thời gian tối đa để giải bài toán, giá trị mặc định là 100 Max Time giây Số lần lặp tối đa để giải bài toán, giá trị mặc định là 100 Iterations lần Độ chính xác của bài toán. Tại đây có thể nhập vào các số trong khoảng 0 và 1. Số càng gần 0 thì độ chính xác Constraint Precision càng cao. Giá trị này điều chỉnh sai số cho tập ràng buộc. Giá trị mặc định là 1 phần triệu Độ hội tụ. Tại đây nhập vào các số trong khoảng 0 đến 1. Convergence Giá trị càng gần 0 thì độ chính xác cao hơn và cần thời gian nhiều hơn. Chọn khi bài toán có sự khác biệt lớn giữa dữ liệu nhập Use Automatic Scaling và xuất Lê Viết Mẫn - lvman@hce.edu.vn 12 Giải PT và HPT Wednesday, May 8, 13 Options (2/2) Tham số Giải thích Chọn nếu muốn Solver tạm dừng lại và hiển thị kết quả Show Iteration Results sau mỗi lần lặp Chọn cách để ước lượng hàm mục tiêu và các ràng buộc Forward : được dùng rất phổ biến, khi đó các giá trị của ràng buộc biến đổi chậm Derivatives Central : dùng khi các giá trị của ràng buộc biến đổi nhanh và được dùng khi Solver báo không thể cải tiến kết quả thu được Population Size Kích thước quần thể Random Seed Giá trị lõi của hàm lấy giá trị ngẫu nhiên Mutation Rate Tốc độ biến dị Lê Viết Mẫn - lvman@hce.edu.vn 13 Giải PT và HPT Wednesday, May 8, 13 Thông báo lỗi của Solver Thông báo Giải thích Bài toán không có lời giải chấp nhận được hoặc các giá Solver could not find trị khởi đầu của các ô chứa biến số quá xa các giá trị tối feasible solution ưu. Có thể thay đổi giá trị khởi đầu để giải lại bài toán Số bước lặp đã đạt đến giá trị lựa chọn trong mục options The maximum iteration was mà chưa tìm được tối ưu. Có thể tăng số bước lặp trong reached, continue anyway ? Solver options để giải bài toán The maximum time limit Thời gian chạy vượt quá giá trị lựa chọn trong mục was reached, continue options mà chưa tìm được tối ưu. Có thể tăng thời gian anyway ? trong Solver options để giải bài toán. Lê Viết Mẫn - lvman@hce.edu.vn 14 Giải PT và HPT Wednesday, May 8, 13 Giải hệ phương trình Ma trận Lê Viết Mẫn - lvman@hce.edu.vn 15 Giải PT và HPT Wednesday, May 8, 13 Giải hpt bằng ma trận ⎧ 3x + y + 2z = 34 ⎪ ⎨ x + y + 2z = 18 ⎪ x + 3y + 2z = 22 ⎩ 3 1 2 x 34 Biểu diễn bằng ma trận 1 1 2 * y = 18 1 3 2 z 22 hoặc A * X = B X = A−1B Lê Viết Mẫn - lvman@hce.edu.vn 16 Giải PT và HPT Wednesday, May 8, 13 Một số khái niệm Cho ma trận Ma trận đơn vị ⎛ ⎞ a11 a12 a1n ⎛ 1 0 0 ⎞ ⎜ ⎟ ⎜ ⎟ a21 a22 a2n 0 1 0 A = ⎜ ⎟ I = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ 0 0 1 ⎟ ⎝ an1 an2 ann ⎠ ⎝ ⎠ Tích hai ma trận Hai ma trận chỉ nhân được với nhau khi số cột của ma trận đứng trước bằng với số dòng của ma trận đứng sau n cij = ∑aikbkj k =1 Ma trận nghịch đảo A * A−1 = I Lê Viết Mẫn - lvman@hce.edu.vn 17 Giải PT và HPT Wednesday, May 8, 13 MDETERM Matrix determinant • Chức năng : tính định thức của ma trận • Cú pháp MDETERM (array) Lê Viết Mẫn - lvman@hce.edu.vn 18 Giải PT và HPT Wednesday, May 8, 13 MINVERSE Matrix inverse • Chức năng : tính ma trận nghịch đảo • Cú pháp MINVERSE (array) Lê Viết Mẫn - lvman@hce.edu.vn 19 Giải PT và HPT Wednesday, May 8, 13 MMULT Matrix multiply • Chức năng : nhân hai ma trận • Cú pháp MMULT (array1, array2) Lê Viết Mẫn - lvman@hce.edu.vn 20 Giải PT và HPT Wednesday, May 8, 13 Giải hpt bằng ma trận ⎧ 3x + y + 2z = 34 ⎪ ⎨ x + y + 2z = 18 ⎪ x + 3y + 2z = 22 ⎩ Lê Viết Mẫn - lvman@hce.edu.vn 21 Giải PT và HPT Wednesday, May 8, 13 Cảm ơn sự chú ý Câu hỏi ? Lê Viết Mẫn - lvman@hce.edu.vn 22 Giải PT và HPT Wednesday, May 8, 13
File đính kèm:
 bai_giang_tin_hoc_ung_dung_chuong_giai_phuong_trinh_va_he_ph.pdf
bai_giang_tin_hoc_ung_dung_chuong_giai_phuong_trinh_va_he_ph.pdf

