Bài giảng Tin học nhóm ngành Nông-Lâm-Ngư & Môi trường - Chương 5: Xử lý phân tích số liệu thống kê Bằng MS Excel 2010
Nội dung chính
Một số kiến thức dữ liệu thống kê
Công cụ phân tích dữ liệu thống kê trong Excel
Phân tích số liệu thống kê
Thống kê mô tả
Tổ chức đồ
Tính hệ số tương quan và phương trình hồi quy
So sánh 2 mẫu (Kiểm định giả thuyết)Một số kiến thức dữ liệu thống kê
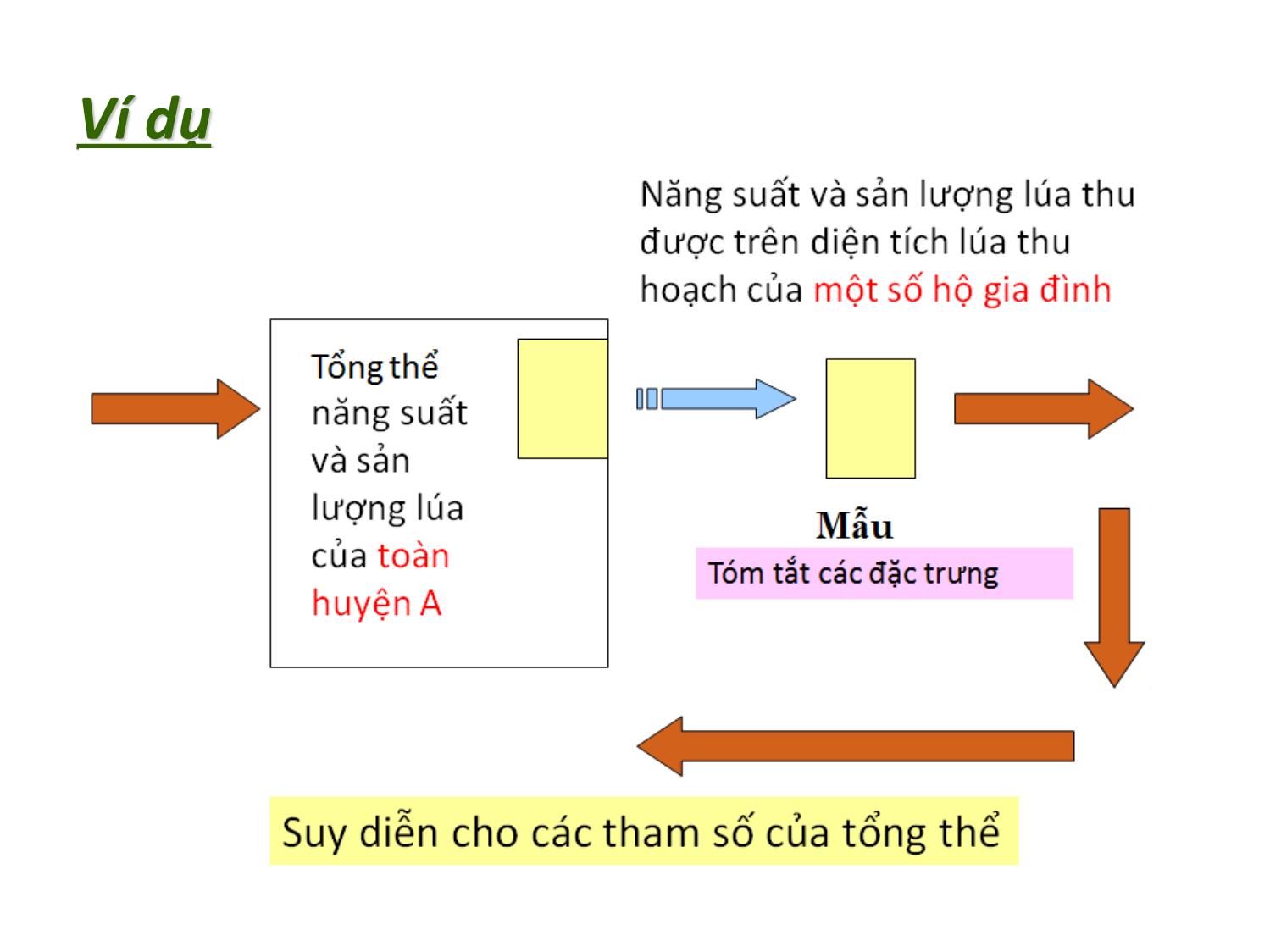
Một đề cương nghiên cứu
oGiả thuyết
oThiết kế một thí nghiệm hay cuộc điều tra
oQuy trình chọn mẫu
oPhương pháp và cách thức điều tra
oPhân tích số liệu
oBáo cáo kết quả
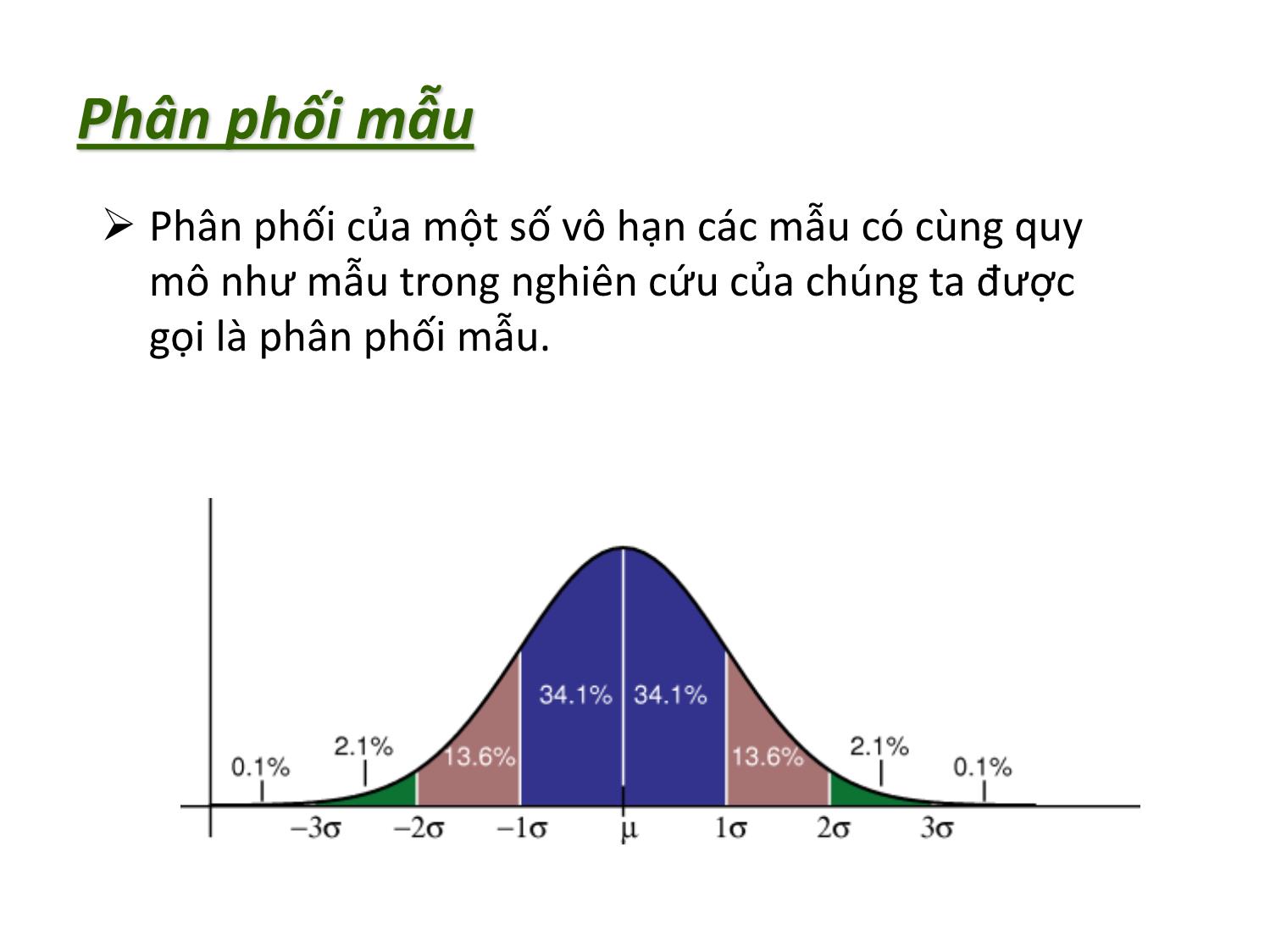
Tư tưởng chính của thống kê suy rộng là lấy mẫu từ
một tổng thể và sau đó sử dụng kết quả phân tích
các thông tin từ mẫu này để suy rộng ra cho tổng
thể nghiên cứu.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Tin học nhóm ngành Nông-Lâm-Ngư & Môi trường - Chương 5: Xử lý phân tích số liệu thống kê Bằng MS Excel 2010", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Tin học nhóm ngành Nông-Lâm-Ngư & Môi trường - Chương 5: Xử lý phân tích số liệu thống kê Bằng MS Excel 2010

ệu
Input Bin: miền phân tổ
Labels : nhãn ở hàng đầu nếu có
Output range: miền kết quả
Pareto: tần số sắp xếp giảm dần
Cumulative Percentage: tần suất cộng dồn %
Chart output: biểu đồ
OK
Ví dụ:
Dựa trên 30 số liệu về chiều dài cá, tạo miền phân tổ
(Bin) từ ô D2 tới ô D12 (kể cả nhãn), giá trị cận dưới là
10, cận trên là 55, giá trị bước tăng 5.
Ví dụ:
Chọn Tools> Data Analysis> Histogram
Ví dụ:
Kết quả
Phân tích kết quả
Tần số số liệu rơi vào từng khoảng được ghi ở cận trên của khoảng.
Chẳng hạn, có 2 số liệu thuộc vào khoảng (10, 15], vì vậy số 2 được ghi
tương ứng với số 15 là cận trên
Nhìn vào hình 5 ta có thể thấy trong khoảng nào số liệu xuất hiện nhiều
nhất
Tính hệ số tương quan
Excel cho phép tính hệ số tương quan đơn giữa các
biến với các số liệu mẫu thu thập được sắp xếp thành
một bảng gồm n hàng, n cột (trên mỗi cột là số liệu
mẫu của một biến)
Thao tác:
Chọn Tools>Data Analysis>Correlation và khai báo các mục:
Input range: miền dữ liệu kể cả nhãn
Grouped by: Column (số liệu theo cột)
Labels in first row: tích chọn nếu có nhãn ở hàng đầu
Output range: miền xuất kết quả
OK
Ví dụ:
Đánh giá mối tương quan giữa các đặc tính dài bông, số
hạt, số bông với năng suất lúa
Thao tác:
Tools>Data analysis>Correlation
Khai báo các mục
Ví dụ:
Kết quả
Dài bông P1000 Số bông Năng suất
Dài bông 1
P1000 0.233314 1
Số bông −0.22056 0.340772 1
Năng suất 0.200805 0.66632 0.661379 1
Phân tích kết quả
Hệ số tương quan của hàng và cột ghi ở ô giao giữa hàng và cột
Hệ số tương quan âm (< 0) thể hiện mối tương quan nghịch biến (chẳng
hạn tương quan giữa “dài bông” và “số bông” là nghịch biến)
Các hệ số tương quan có giá trị tuyệt đối xấp xỉ 0.75 trở lên thể hiện mối
tương quan tuyến tính mạnh giữa hai biến (tương quan giữa “năng suất”
và “P1000” có thể tạm coi là tương quan tuyến tính mạnh).
Tìm phương trình hồi quy
Excel cho phép tìm PT hồi quy tuyến tính đơn:
= +
và hồi quy tuyến tính bội:
= 0 + 1 1 + ⋯ + 푛 푛
Các biến độc lập chứa trong 푛 cột, biến phụ thuộc để
trong một cột, các giá trị tương ứng giữa biến độc lập và
biến phụ thuộc được xếp trên cùng một hàng
Tìm phương trình hồi quy
Thao tác:
Chọn Tools>Data Analysis>Regression và khai báo các mục:
Input y range: miền dữ liệu biến y
Input x range: miền dữ liệu các biến x
Label: tích chọn nếu có nhãn ở hàng đầu
Confidence level: 95% ( độ tin cậy 95%)
Constant in zero: tích chọn nếu hệ số tự do a = 0
Output range: miền xuất kết quả
Residuals: tích chọn để hiện phần dư hay sai lệch giữa y thực nghiệm và y
theo hồi quy
Standardized residuals: tích chọn để hiện phần dư đã chuẩn hoá
Residuals plot: tích chọn để hiện đồ thị phần dư
Line fit plots: tích chọn để hiện đồ thị các đường dự báo
Normal probability plot: tích chọn để hiện đồ thị phần dư đã chuẩn hoá
OK
Ví dụ:
Tìm phương trình hồi qui:
= 0 + 1 1 + 2 2 + 3 3
của năng suất lúa y phụ thuộc tuyến tính vào độ dài bông ( 1),
trọng lượng 1000 hạt ( 2) và số bông/một cây ( 3) với các số liệu
Ví dụ:
Kết quả
Ví dụ:
Phân tích kết quả
Nếu hệ số tương quan bội xấp xỉ 0.75 hoặc lớn hơn thì mô hình hồi quy
tuyến tính là thích hợp (ngược lại nên tìm mô hình khác)
Trong ví dụ này hệ số tương quan bội là 0.8375 nên mô hình tuyến tính
được coi là thích hợp
Hệ số tương quan R square trong ví dụ là 0.7014 cho biết 70.14% sự biến
động của y là do các yếu tố x1, x2, x3 gây nên. Hệ số Adjusted R square
là 62.00% không sát gần với R square chứng tỏ không phải tất cả các
biến đưa vào là thực sự cần thiết
F thực nghiệm là 8.6142 ứng với xác suất 0.00316 nhỏ hơn mức xác suất
{ nghĩa 0.05 nên phương trình hồi quy tuyến tính được chấp nhận
Nhìn vào các hệ số của các biến ta viết được đường hồi quy dự báo.
Trong ví dụ phương trình hồi quy là:
y =− 3.61899 + 0.085345x1 + 0.081163x2 + 0.02083x3
Tuy nhiên căn cứ vào các xác suất cho ở cột P-value thì hệ số của x1 là
không đáng tin cậy, vì xác suất tương ứng > 0.05 (mức { nghĩa đã chọn).
Trong trường hợp này, cần tiến hành lọc bớt biến x1 để được đường hồi
quy với các hệ số đều có { nghĩa
So sánh mẫu
Bài toán ở đây cần so sánh hai mẫu thông qua việc kiểm
định giả thuyết 0: 1 = 2(Kz vọng của biến X và biến Y
bằng nhau) với đối thuyết 1: 1 ≠ 2 ở mức { nghĩa 훼
trong trường hợp kiểm định hai phía. Nếu kiểm định một
phía thì đối thuyết
. 1: 1 < 2 ( < )
. 1: 1 > 2 ( > )
So sánh 2 mẫu độc lập khi biết phương sai
Thao tác:
Data >Data Analysis > z-Test: Two Sample for Means,
Input Variable 1 Range: miền chứa số liệu biến 1, kể cả tên hàng
đầu của mẫu quan sát
Input Variable 2 Range: miền chứa số liệu biến 2, kể cả tên hàng
đầu của mẫu quan sát
Labels: tích chọn nếu chứa tên biến
Hypothesized means difference: giả thuyết về hiệu hai trung bình
của hai tổng thể. Nếu lấy giả thuyết H0: m1 = m2 thì ghi 0. Nếu lấy
giả thuyết H1: m1 = m2+d (d là 1 số nào đó) thì ghi d.
2
Variable 1 variance: phương sai của biến 1 (nhập 휎1 )
2
Variable 2 variance: phương sai của biến 2 (nhập 휎2 )
Output Range: chọn miền trống để đưa ra kết quả
Ví dụ:
Thực hiện thí nghiệm với mẫu 1 có 10 số liệu quan sát được,
mẫu 2 có 12 quan sát ta có bảng số liệu sau, biết phương sai
của biến 1 là 2.7, của biến 2 là 2.6. Cho biết kết quả so sánh 2
mẫu độc lập.
Ví dụ:
Kết quả
Phân tích kết quả
Trung bình của mẫu
Phương sai đã cho
Số quan sát n1 và n2
Giá trị z thực nghiệm:
Giá trị P một phía và giá trị P hai phía
Giá trị z l{ thuyết (tới hạn) một phía và hai phía
Trong ví dụ 5 ta thấy: giá trị z thực nghiệm 0.14335 nhỏ
hơn z lý thuyết (tới hạn) một phía 1.64485 cũng như z lý
thuyết hai phía 1.95996 (giá trị P một phía và hai phía đều
lớn hơn mức ý nghĩa α = 0.05).
Kết luận: kỳ vọng của hai biến không khác nhau
So sánh 2 mẫu kiểu cặp đôi
Ví dụ:
Nếu mỗi một ổ chim cân trọng lượng chim cái, trọng lượng chim đực, lúc
đó với n ổ chim ta được hai mẫu quan sát kiểu cặp đôi của hai tổng thể
chim cái và chim đực. Nếu lấy một số chim đực ngẫu nhiên trong nhiều
chim đực từ nhiều ổ và lấy một số chim cái ngẫu nhiên trong nhiều chim
cái từ nhiều ổ thì có hai mẫu quan sát độc lập.
Nếu ta đem 10 mẫu đất, mỗi mẫu chia đôi, một nửa giao cho phòng
phân tích A thực hiện, nửa kia giao cho phòng phân tích B thì thu được
số liệu cặp đôi để so sánh kết quả của hai phòng phân tích.
Nếu ta đem hai giống lúa cấy trên một số ruộng, mỗi ruộng chia đôi, một
nửa cấy giống A, một nửa cấy giống B thì cũng có hai mẫu cặp đôi để so
sánh.
So sánh 2 mẫu kiểu cặp đôi
Thao tác
Data >Data Analysis > t-Test: Paired Two Sample for Means
Điền tham số
Input Variable 1 Range: miền chứa số liệu của biến 1 (kể cả tên)
Input Variable 2 Range: miền chứa số liệu của biến 2 (kể cả tên)
Labels: Tích chọn nếu hàng đầu chứa tên biến
Hypothesized means difference: giả thiết về hiệu hai trung bình
của hai tổng thể. Nếu lấy giả thuyết H0: m1 = m2 thì ghi 0. Nếu lấy
giả thuyết H0: m1 = m+ d (d là một số nào đó) thì ghi d.
Output Range: Chọn miền trống để hiện kết quả
OK
Ví dụ:
Phân tích mẫu cặp đôi sau
Ví dụ:
Do t thực nghiệm lớn hơn t lý thuyết một phía cũng như hai
phía (giá trị P một phía và hai phía đều nhỏ hơn mức ý nghĩa
α = 0.05), nên trong ví dụ trên ta chấp nhận giả thuyết H1
So sánh 2 mẫu độc lập
Giả thiết 2 phương sai bằng nhau
Chọn Data>Data Analysis > t-Test: Two-Sample
Assuming Equal Variances
Giả thiết 2 phương sai khác nhau
Chọn Data>Data Analysis > t-Test: Two-Sample
Assuming Unequal Variances
Nhập các tham số tương tự
Phân tích kết quả?
Ví dụ:
Phân tích kết quả
Phân tích phương sai
Phân tích phương sai là công cụ chủ yếu để phân tích
các số liệu khi theo dõi ảnh hưởng của các nhân tố
(factor) trong thí nghiệm và ảnh hưởng tương tác của
chúng lên một (hay nhiều) chỉ số đầu ra.
o Phân tích một nhân tố: Thí nghiệm ngẫu nhiên, mỗi
mức lặp lại một số lần
o Phân tích 2 nhân tố: Thí nghiệm trực giao
Phân tích phương sai một nhân tố
PT ảnh hưởng của các mức của nhân tố tới kết quả
Ví dụ: ảnh hưởng của các công thức cho ăn đến năng suất thịt
lợn, ảnh hưởng của các công thức phun thuốc sâu đến tỷ lệ sâu
bệnh ...
Thao tác:
Tools>Data Analysis > Anova: Single Factor
Nhập tham số
Input range: miền dữ liệu vào (bao trùm toàn bộ các ô chứa tên
mức và các số liệu)
Grouped by: Columns (theo cột) hoặc Rows (theo hàng)
Label in First column: nhãn hàng đầu
Alpha: 0.05 (mức { nghĩa α)
Output range: miền xuất kết quả ra
Phân tích phương sai một nhân tố
Phân tích kết quả:
Kết quả là các thống kê cơ bản cho từng mức (trung bình,
độ lệch chuẩn...) và bảng phân tích phương sai
Nếu giá trị xác suất P-value F
l{ thuyết) thì các công thức có tác động khác nhau tới kết
quả, ngược lại các công thức không có khác biệt đáng kể
Nếu kết luận các công thức có tác động khác nhau tới kết
quả thì phải tiến hành bước tiếp theo là so sánh các công
thức để rút ra công thức nào tốt nhất
Phân tích phương sai một nhân tố
Số liệu được điền theo cột hoặc theo hàng (nếu vào theo hàng
thì mỗi hàng ứng với một mức của nhân tố), ô đầu tiên ghi tên
mức, các ô tiếp theo ghi số liệu.
Chọn Tools>Data Analysis > Anova: Single Factor
Nhập các tham số:
Input range: khai báo miền dữ liệu vào (một chữ nhật bao trùm toàn
bộ các ô chứa tên mức và toàn bộ các số liệu).
Grouped by: Columns (số liệu theo cột) hoặc Rows (số liệu theo hàng).
Label in First column: nhãn hàng đầu.
Alpha: 0.05 (mức { nghĩa α)
Output range: miền xuất kết quả
Phương tích phương sai một nhân tố:
Phân tích kết quả
Kết quả in ra gồm các thống kê cơ bản cho từng mức (trung
bình, độ lệch chuẩn...) và bảng phân tích phương sai.
Nếu giá trị xác suất P-value F
lý thuyết) thì các công thức có tác động khác nhau tới kết
quả, ngược lại các công thức không có khác biệt đáng kể.
Nếu kết luận các công thức có tác động khác nhau tới kết
quả thì phải tiến hành bước tiếp theo là so sánh các công
thức để rút ra công thức nào tốt nhất.
Ví dụ:
Thí nghiệm ảnh hưởng của các loại thuốc đến năng
suất lúa (11 loại thuốc là T1 đến T11, 4 cột số liệu là
năng suất thu được), số liệu thu được cho trong bảng
Ví dụ:
Kết quả
Chương 6:
Biểu diễn kết quả thống kê
trong báo cáo khoa học
Nội dung chính
Báo cáo phân tích số liệu
Danh mục
Bảng biểu
Biểu đồ
Các thao tác trên biểu đồ
Hiệu chỉnh và định dạng biểu đồ
Các thao tác với chuỗi số liệu trong biểu đồ
Báo cáo phân tích số liệu
Giải thích rõ các thông tin
Lựa chọn cách trình bày
Báo cáo đó nộp cho ai?
Ai là người sẽ đọc nó?
Báo cáo phân tích số liệu
Bố cục:
(1) Tên của báo cáo, người/đơn vị báo cáo, nơi và ngày viết. Tên
bản báo cáo súc tích, ngắn gọn, nhưng rõ ràng
(2) Phần giới thiệu: chỉ ra vấn đề đặt ra cần phải giải quyết và
những câu hỏi nghiên cứu vấn đề, những giả thuyết cần kiểm tra
(3) Danh mục các đặc trưng của cuộc điều tra: Kiểu điều tra; công
cụ sử dụng trong điều tra; bao nhiêu câu hỏi; bao nhiêu
mẫu/quan sát; các vấn đề liên quan khác
(4) Giải thích phương pháp điều tra: Thiết kế điều tra; lựa chọn
mẫu; phân tích
(5) Các kết quả liên quan đến vấn đề nghiên cứu
(6) Các kết luận
(7) Các kiến nghị rút ra từ nghiên cứu
Báo cáo phân tích số liệu
Việc phân tích số liệu là để hiểu được quá khứ, hiện
tại nhằm mục đích phục vụ cho tương lai do vậy một
lời giải thích, phân tích rõ ràng sẽ giúp cho người đọc
thấy được điều gì sẽ có thể diễn ra trong tương lai.
Đối với một báo cáo khoa học cách thức trình bày kết
quả phân tích phải hết sức linh hoạt giữa bảng biểu
và đồ thị để tránh sự nhàm chán và để thể hiện tốt
nhất những { tưởng mà số liệu có thể thông tin cho
ta biết.
Danh mục
Danh mục là công cụ đơn giản và rất hữu dụng trong
việc báo cáo kết quả
o (1) Chỉ sử dụng một vài từ để thể hiện { chính, không nên
sử dụng cả đoạn văn dài
o (2) Đảm bảo sự thống nhất trước sau, tránh việc khi thì sử
dụng một vài từ khi thì sử dụng cả câu
o (3) Để khoảng trống giữa các mục của danh mục
o (4) Sử dụng thống nhất các kí hiệu hay gạch đầu dòng
o (5) Trong cùng một bản báo cáo nên sử dụng cùng một loại
k{ hiệu
Bảng biểu
Dạng bảng thường được dùng để thể hiện kết quả
của một hoặc một vài chỉ tiêu nghiên cứu tương ứng
với các tiêu chí khác nhau.
Lưu {:
(1) Đầu mục của các cột cần phải xác định là các tiêu chí
quan trọng cho việc so sánh
(2) Không nên có quá nhiều cột hay dòng trong một bảng
(3) Nên sử dụng các k{ hiệu để minh hoạ cho mức độ tin
cậy/{ nghĩa thống kê
(4) Nên có nguồn trích dẫn của số liệu trong bảng
(5) Trong cùng một bảng các số liệu cần phải có sự liên hệ
với nhau
Biểu đồ
Biểu đồ là phương pháp trình bày số liệu nhằm giúp
người đọc dễ hiểu và nắm bắt vấn đề nhanh nhất
Các dạng biểu đồ
Dạng bánh
Dạng cột
Dạng đồ thị
Dạng tọa độ v.v...
Biểu đồ
Các thao tác trên biểu đồ
Hiệu chỉnh và định dạng biểu đồ
Các thao tác với chuỗi số liệu trong biểu đồ
Biểu đồ
Các thao tác
Chọn Insert > Chart > [Loại biểu đồ] > OK
Ví dụ biểu đồ hình cột (Column)
Microsoft Office tự động tạo một mẫu biểu đồ và bật
chương trình Excel để chỉnh sửa số liệu
Biểu đồ
Ta cũng có thể chỉnh số liệu bằng cách: ấn chuột phải trên
biểu đồ > chọn Edit data
Hiển thị nhãn số liệu bằng cách: ấn chuột phải >
chọn Add data labels
6
5
5 4.3 4.4 4.5
4 3.5
3 2.8 Loại A
3 2.4 2.5
2 2 Loại B
2 1.8
Loại C
1
0
Mẫu 1 Mẫu 2 Mẫu 3 Mẫu 4
Biểu đồ
Biểu đồ hình bánh (Pie)
Tên biểu đồ
10
Loại 1
20
44 Loại 2
Loại 3
Loại 4
26
Biểu đồ
Biểu đồ dạng đồ thị (Line)
6
5
4.4
4
Series 1
3 2.8
2.4 Series 2
2
1.8 Series 3
1
0
Nhãn 1 Nhãn 2 Nhãn 3 Nhãn 4
Biểu đồ
Biểu đồ dạng Area
50
40
30
Series 2
20 Series 1
10
0
01/05/2002 01/06/2002 01/07/2002 01/08/2002 01/09/2002
Biểu đồ
Biểu đồ dạng tọa độ
Y-Values
3.5
3
2.5
2
1.5 Y-Values
1
0.5
0
0 1 2 3
Biểu đồ
Biểu đồ dạng bóng
Y-Values
4
3.5
3
2.5
2
Y-Values
1.5
1
0.5
0
0 1 2 3 4
Biểu đồ
Biểu đồ dạng mạng (Radar)
01/05/2002
40
30
20
01/09/2002 01/06/2002
10
Series 1
0
Series 2
01/08/2002 01/07/2002File đính kèm:
 bai_giang_tin_hoc_nhom_nganh_nong_lam_ngu_moi_truong_chuong.pdf
bai_giang_tin_hoc_nhom_nganh_nong_lam_ngu_moi_truong_chuong.pdf

